5.4 Properties of Logarithms
In Section 5.3, we introduced the logarithmic functions as inverses of exponential functions and discussed a few of their functional properties from that perspective. In this section, we explore the algebraic properties of logarithms. Historically, these have played a huge role in the scientific development of our society since, among other things, they were used to develop analog computing devices called slide rules which enabled scientists and engineers to perform accurate calculations leading to such things as space travel and the moon landing.
As we shall see shortly, logs inherit analogs of all of the properties of exponents you learned in Algebra. We first extract two properties from Theorem 5.5 to remind us of the definition of a logarithm as the inverse of an exponential function.
Theorem 5.6 Inverse Properties of Exponential and Logarithmic Functions
Let ![]() ,
, ![]() .
.
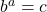 if and only if
if and only if 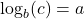 . That is,
. That is, 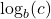 is the exponent you put on
is the exponent you put on  to obtain
to obtain  .
.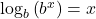 for all
for all  and
and 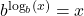 for all
for all 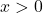
Next, we spell out what it means for exponential and logarithmic functions to be one-to-one.
Theorem 5.7 One-to-one Properties of Exponential and Logarithmic Functions
Let ![]() and
and ![]() where
where ![]() ,
, ![]() . Then
. Then ![]() and
and ![]() are one-to-one and
are one-to-one and
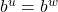 if and only if
if and only if  for all real numbers
for all real numbers 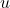 and
and 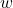 .
.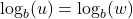 if and only if
if and only if  for all real numbers
for all real numbers 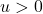 ,
, 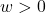 .
.
Next, we re-state Theorem 5.4 for reference below.
Algebraic Properties of Exponential Functions
Let ![]() be an exponential function (
be an exponential function (![]() ,
, ![]() ) and let
) and let ![]() and
and ![]() be real numbers.
be real numbers.
- Product Rule:
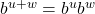
- Quotient Rule:
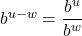
- Power Rule:
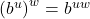
To each of these properties of listed in Theorem 5.4, there corresponds an analogous property of logarithmic functions. We list these below in our next theorem.
Theorem 5.8 Algebraic Properties of Exponential Functions
Let ![]() be a logarithmic function (
be a logarithmic function (![]() ,
, ![]() ) and let
) and let ![]() and
and ![]() be real numbers.
be real numbers.
- Product Rule:
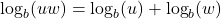
- Quotient Rule:
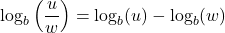
- Power Rule:
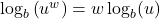
There are a couple of different ways to understand why Theorem 5.8 is true. For instance, consider the product rule: ![]() .
.
Let ![]() ,
, ![]() , and
, and ![]() . Then, by definition,
. Then, by definition, ![]() ,
, ![]() and
and ![]() . Hence,
. Hence, ![]() , so that
, so that ![]() .
.
From a purely functional approach, we can see the properties in Theorem 5.8 as an example of how inverse functions interchange the roles of inputs and outputs.
For instance, the Product Rule for exponential functions given in Theorem 5.4, ![]() , says that adding inputs results in multiplying outputs.
, says that adding inputs results in multiplying outputs.
Hence, whatever ![]() is, it must take the products of outputs from
is, it must take the products of outputs from ![]() and return them to the sum of their respective inputs. The outputs from
and return them to the sum of their respective inputs. The outputs from ![]() are the inputs to
are the inputs to ![]() and vice-versa, thus
and vice-versa, thus ![]() must take products of its inputs to the sum of their respective outputs. This is precisely one way to interpret the Product Rule for Logarithmic functions:
must take products of its inputs to the sum of their respective outputs. This is precisely one way to interpret the Product Rule for Logarithmic functions: ![]() .
.
The reader is encouraged to view the remaining properties listed in Theorem 5.8 similarly.
The following examples help build familiarity with these properties. In our first example, we are asked to `expand’ the logarithms. This means that we read the properties in Theorem 5.8 from left to right and rewrite products inside the log as sums outside the log, quotients inside the log as differences outside the log, and powers inside the log as factors outside the log.[1]
Example 5.4.1
Example 5.4.1.1
Expand the following using the properties of logarithms and simplify. Assume when necessary that all quantities represent positive real numbers.
![]()
Solution:
Expand and simplify ![]() .
.
To expand ![]() , we use the Quotient Rule identifying
, we use the Quotient Rule identifying ![]() and
and ![]() and simplify.
and simplify.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \log_{2}\left(\dfrac{8}{x}\right) & = & \log_{2}(8) - \log_{2}(x) & \text{Quotient Rule} \\ & = & 3 - \log_{2}(x) & \text{Because } 2^{3} = 8 \\ & = & - \log_{2}(x) + 3 & \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4b6d0ea62db3ae08ed66da25b3ae216a_l3.png)
Example 5.4.1.2
Expand the following using the properties of logarithms and simplify. Assume when necessary that all quantities represent positive real numbers.
![]()
Solution:
Expand and simplify ![]() .
.
In the expression ![]() , we have a power (the
, we have a power (the ![]() ) and a product, and the question becomes which property, Power Rule or Product Rule to use first.
) and a product, and the question becomes which property, Power Rule or Product Rule to use first.
In order to use the Power Rule, the entire quantity inside the log must be raised to the same exponent. The exponent ![]() applies only to the
applies only to the ![]() , so we first apply the Product Rule with
, so we first apply the Product Rule with ![]() and
and ![]() . Once the
. Once the ![]() is by itself inside the log, we apply the Power Rule with
is by itself inside the log, we apply the Power Rule with ![]() and
and ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \log_{0.1} \left(10 x^2 \right) & = & \log_{0.1} (10) + \log_{0.1} \left(x^2 \right) & \text{Product Rule} \\[6pt] & = & \log_{0.1} (10)+ 2 \log_{0.1} (x) & \text{Power Rule} \\[6pt] & = & -1 + 2 \log_{0.1} (x) & \text{Because } (0.1)^{-1} = 10 \\[6pt] & = & 2 \log_{0.1} (x) - 1 & \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-21519b4ebc0941393431046e4678c557_l3.png)
Example 5.4.1.3
Expand the following using the properties of logarithms and simplify. Assume when necessary that all quantities represent positive real numbers.
![]()
Solution:
Expand and simplify ![]() .
.
We have a power, quotient and product occurring in ![]() . This time the exponent
. This time the exponent ![]() applies to the entire quantity inside the logarithm, so we begin with the Power Rule with
applies to the entire quantity inside the logarithm, so we begin with the Power Rule with ![]() and
and ![]() .
.
Next, we see the Quotient Rule is applicable, with ![]() and
and ![]() , so we replace
, so we replace ![]() with the quantity
with the quantity ![]() .
.
Because ![]() is being multiplied by
is being multiplied by ![]() , the entire quantity
, the entire quantity ![]() is multiplied by
is multiplied by ![]() .
.
Finally, we apply the Product Rule with ![]() and
and ![]() , and replace
, and replace ![]() with the quantity
with the quantity ![]() , and simplify, keeping in mind that the natural log is log base
, and simplify, keeping in mind that the natural log is log base ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \ln \left(\dfrac{3}{et}\right)^2 & = & 2 \ln \left(\dfrac{3}{et}\right) & \text{Power Rule} \\[6pt] & = & 2 \left[ \ln(3) - \ln(et) \right] & \text{Quotient Rule} \\[6pt] & = & 2 \ln(3) - 2\ln(et) & \\[6pt] & = & 2 \ln(3) - 2\left[\ln(e) + \ln(t)\right] & \text{Product Rule} \\[6pt] & = & 2 \ln(3) - 2\ln(e) - 2 \ln(t) & \\[6pt] & = & 2\ln(3) - 2 - 2 \ln(t) & \text{Because } e^{1} = e \\[6pt] & = & - 2 \ln(t) + 2\ln(3) - 2 & \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-867520baeed52ce7ba87bc587390b2ef_l3.png)
Example 5.4.1.4
Expand the following using the properties of logarithms and simplify. Assume when necessary that all quantities represent positive real numbers.
![Rendered by QuickLaTeX.com \log \sqrt[3]{\dfrac{100 x^2}{yz^5}}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-65dc42fa62a1153ade18052a685004b5_l3.png)
Solution:
Expand and simplify ![Rendered by QuickLaTeX.com \log \sqrt[3]{\dfrac{100 x^2}{yz^5}}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-65dc42fa62a1153ade18052a685004b5_l3.png) .
.
In Theorem 5.8, there is no mention of how to deal with radicals. However, thinking back to Definition 0.3, we can rewrite the cube root as a ![]() exponent. We begin by using the Power Rule[2], and we keep in mind that the common log is log base
exponent. We begin by using the Power Rule[2], and we keep in mind that the common log is log base ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \log \sqrt[3]{\dfrac{100 x^2}{yz^5}} & = & \log \left(\dfrac{100 x^2}{yz^5}\right)^{1/3} & \\ [10pt] & = & \frac{1}{3} \log\left(\dfrac{100 x^2}{yz^5}\right) & \text{Power Rule} \\ [5pt] & = & \frac{1}{3} \left[ \log\left(100x^2\right) - \log\left(yz^5\right) \right] & \text{Quotient Rule} \\[6pt] & = & \frac{1}{3}\log\left(100x^2\right) - \frac{1}{3}\log\left(yz^5\right) & \\[6pt] & = & \frac{1}{3}\left[ \log(100) + \log\left(x^2\right)\right] - \frac{1}{3} \left[ \log(y) + \log\left(z^5\right) \right] & \text{Product Rule} \\[6pt] & = & \frac{1}{3} \log(100) + \frac{1}{3} \log\left(x^2\right) - \frac{1}{3} \log(y) - \frac{1}{3} \log\left(z^5\right) \\[6pt] & = & \frac{1}{3} \log(100) + \frac{2}{3} \log(x) - \frac{1}{3} \log(y) - \frac{5}{3} \log(z) & \text{Power Rule} \\[6pt] & = & \frac{2}{3} + \frac{2}{3} \log(x) - \frac{1}{3} \log(y) - \frac{5}{3} \log(z) & \text{Because } 10^2=100\\[6pt] & = & \frac{2}{3} \log(x) - \frac{1}{3} \log(y) - \frac{5}{3} \log(z) + \frac{2}{3} & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-30eeda111d8bff90408dea731007b075_l3.png)
Example 5.4.1.5
Expand the following using the properties of logarithms and simplify. Assume when necessary that all quantities represent positive real numbers.
![]()
Solution:
Expand and simplify ![]() .
.
At first it seems as if we have no means of simplifying ![]() , as none of the properties of logs addresses the issue of expanding a difference inside the logarithm. However, we may factor
, as none of the properties of logs addresses the issue of expanding a difference inside the logarithm. However, we may factor ![]() thereby introducing a product which gives us license to use the Product Rule. Assuming both
thereby introducing a product which gives us license to use the Product Rule. Assuming both ![]() and
and ![]() , that is,
, that is, ![]() we expand as follows.
we expand as follows.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \log_{117}\left(x^2-4\right) & = & \log_{117} \left[(x+2)(x-2)\right] & \text{Factor} \\[6pt] & = & \log_{117}(x+2) + \log_{117}(x-2) & \text{Product Rule} \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f77b0e1aba0217e070a5e89d7b34454d_l3.png)
A couple of remarks about Example 5.4.1 are in order. First, if we take a step back and look at each problem in the foregoing example, a general rule of thumb to determine which log property to apply first when faced with a multi-step problem is to apply the logarithm properties in the `reverse order of operations.’
For example, if we were to substitute a number for ![]() into the expression
into the expression ![]() , we would first square the
, we would first square the ![]() , then multiply by
, then multiply by ![]() . The last step is the multiplication, which tells us the first log property to apply is the Product Rule. The last property of logarithm to apply would the be the power rule applied to
. The last step is the multiplication, which tells us the first log property to apply is the Product Rule. The last property of logarithm to apply would the be the power rule applied to ![]() .
.
Second, the equivalence ![]() is valid only if
is valid only if ![]() . Indeed, the functions
. Indeed, the functions ![]() and
and ![]() have different domains, and, hence, are different functions.[3] In general, when using log properties to expand a logarithm, we may very well be restricting the domain as we do so.
have different domains, and, hence, are different functions.[3] In general, when using log properties to expand a logarithm, we may very well be restricting the domain as we do so.
One last comment before we move to reassembling logs from their various bits and pieces. The authors are well aware of the propensity for some students to become overexcited and invent their own properties of logs like ![]() , which simply isn’t true, in general. The unwritten[4] property of logarithms is that if it isn’t written in a textbook, it probably isn’t true.
, which simply isn’t true, in general. The unwritten[4] property of logarithms is that if it isn’t written in a textbook, it probably isn’t true.
Example 5.4.2
Example 5.4.2.1
Use the properties of logarithms to write the following as a single logarithm.
![]()
Solution:
Whereas in Example 5.4.1 we read the properties in Theorem 5.8 from left to right to expand logarithms, in this example we read them from right to left.
Write ![]() as a single logarithm.
as a single logarithm.
The difference of logarithms requires the Quotient Rule:
![]()
Example 5.4.2.2
Use the properties of logarithms to write the following as a single logarithm.
![]()
Solution:
Whereas in Example 5.4.1 we read the properties in Theorem 5.8 from left to right to expand logarithms, in this example we read them from right to left.
Write ![]() as a single logarithm.
as a single logarithm.
In the expression, ![]() , we have both a sum and difference of logarithms.
, we have both a sum and difference of logarithms.
Before we use the product rule to combine ![]() , we note that we need to apply the Power Rule to rewrite the coefficient
, we note that we need to apply the Power Rule to rewrite the coefficient ![]() as the power on
as the power on ![]() . We then apply the Product and Quotient Rules as we move from left to right.
. We then apply the Product and Quotient Rules as we move from left to right.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \log(x) + 2\log(y) - \log(z) & = & \log(x) + \log\left(y^2\right) - \log(z) & \text{Power Rule} \\ [6pt] & = & \log\left(xy^2\right) - \log(z) & \text{Product Rule} \\ [10pt] & = & \log\left( \dfrac{xy^2}{z}\right) & \text{Quotient Rule} \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-cfafecdd622a8f1f557acff133c97e4e_l3.png)
Example 5.4.2.3
Use the properties of logarithms to write the following as a single logarithm.
![]()
Solution:
Whereas in Example 5.4.1 we read the properties in Theorem 5.8 from left to right to expand logarithms, in this example we read them from right to left.
Write ![]() as a single logarithm.
as a single logarithm.
We begin to rewrite ![]() by applying the Power Rule:
by applying the Power Rule: ![]() .
.
In order to continue, we need to rewrite ![]() as a logarithm base
as a logarithm base ![]() . From Theorem 5.6, we know
. From Theorem 5.6, we know ![]() . Rewriting
. Rewriting ![]() this way paves the way to use the Product Rule.
this way paves the way to use the Product Rule.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 4\log_{2}(x) + 3 & = & \log_{2}\left(x^4\right) + 3 & \text{Power Rule} \\[6pt] & = & \log_{2}\left(x^4\right) + \log_{2}\left(2^3\right)& \text{Because } 3 = \log_{2}\left(2^3\right) \\[6pt] & = & \log_{2}\left(x^4\right) + \log_{2}(8)& \\[6pt] & = & \log_{2}\left( 8x^4\right) & \text{Product Rule} \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f1565a8caecfde60525a11ec170ff5ee_l3.png)
Example 5.4.2.4
Use the properties of logarithms to write the following as a single logarithm.
![]()
Solution:
Whereas in Example 5.4.1 we read the properties in Theorem 5.8 from left to right to expand logarithms, in this example we read them from right to left.
Write ![]() as a single logarithm.
as a single logarithm.
To get started with ![]() , we rewrite
, we rewrite ![]() as
as ![]() . We can then use the Power Rule to obtain
. We can then use the Power Rule to obtain ![]() .
.
As in the previous problem, in order to continue, we need to rewrite ![]() as a natural logarithm. Theorem 5.6 gives us
as a natural logarithm. Theorem 5.6 gives us ![]() . Hence,
. Hence,
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} -\ln(t) - \frac{1}{2} & = & (-1)\ln(t) - \frac{1}{2} & \\[6pt] & = & \ln\left(t^{-1}\right) - \frac{1}{2} & \text{Power Rule} \\[6pt] & = & \ln\left(t^{-1}\right) - \ln\left(e^{1/2}\right) & \text{Because } \frac{1}{2} = \ln\left(e^{1/2}\right) \\[6pt] & = & \ln\left(t^{-1}\right) - \ln\left(\sqrt{e} \right) & \\[6pt] & = & \ln\left(\dfrac{t^{-1}}{\sqrt{e}}\right) & \text{Quotient Rule} \\[10pt] & = & \ln\left(\dfrac{1}{t\sqrt{e}}\right) & \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-3233c77b6bc20fb58a5e70393d83da27_l3.png)
As we would expect, the rule of thumb for re-assembling logarithms is the opposite of what it was for dismantling them. That is, to rewrite an expression as a single logarithm, we apply log properties following the usual order of operations: first, rewrite coefficients of logs as powers using the Power Rule, then rewrite addition and subtraction using the Product and Quotient Rules, respectively, as written from left to right.
Additionally, we find that using log properties in this fashion can increase the domain of the expression. For example, we leave it to the reader to verify the domain of ![]() is
is ![]() but the domain of
but the domain of ![]() is
is ![]() . We’ll need to keep this in mind in Section 5.6 when such manipulations could result in extraneous solutions.
. We’ll need to keep this in mind in Section 5.6 when such manipulations could result in extraneous solutions.
The two logarithm buttons commonly found on calculators are the `LOG’ and `LN’ buttons which correspond to the common and natural logs, respectively. Suppose we wanted an approximation to ![]() . The answer should be a little less than
. The answer should be a little less than ![]() , (Can you explain why?) but how do we coerce the calculator into telling us a more accurate answer? We need the following theorem.
, (Can you explain why?) but how do we coerce the calculator into telling us a more accurate answer? We need the following theorem.
Theorem 5.9 Change of Base Formulas
Let ![]() ,
, ![]() .
.
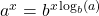 for all real numbers
for all real numbers  .
.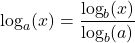 for all real numbers
for all real numbers 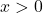 .
.
To prove these formulas, consider ![]() . Using the Power Rule, we can rewrite
. Using the Power Rule, we can rewrite ![]() as
as ![]() . Following this with the Inverse Properties in Theorem 5.6, we get
. Following this with the Inverse Properties in Theorem 5.6, we get
![]()
To verify the logarithmic form of the property, we use the Power Rule and an Inverse Property to get:
![]()
We get the result by dividing both sides of the equation ![]() by
by ![]() .
.
Of course, the authors can’t help but point out the inverse relationship between these two change of base formulas. To change the base of an exponential expression, we multiply the input by the factor ![]() . To change the base of a logarithmic expression, we divide the output by the factor
. To change the base of a logarithmic expression, we divide the output by the factor ![]() .
.
While, in the grand scheme of things, both change of base formulas are really saying the same thing, the logarithmic form is the one usually encountered in Algebra, while the exponential form isn’t usually introduced until Calculus.
Example 5.4.3
Example 5.4.3.1
Use an appropriate change of base formula to convert the following expressions to ones with the indicated base.
![]() to base
to base ![]()
Solution:
Convert ![]() to an equivalent expression base
to an equivalent expression base ![]() .
.
We apply the Change of Base formula with ![]() and
and ![]() to obtain
to obtain ![]() .
.
Example 5.4.3.2
Use an appropriate change of base formula to convert the following expressions to ones with the indicated base.
![]() to base
to base ![]()
Solution:
Convert ![]() to an equivalent expression base
to an equivalent expression base ![]() .
.
Here, ![]() and
and ![]() so we have
so we have ![]() .
.
Example 5.4.3.3
Use an appropriate change of base formula to convert the following expressions to ones with the indicated base.
![]() to base
to base ![]()
Solution:
Convert ![]() to an equivalent expression base
to an equivalent expression base ![]() .
.
Applying the change of base with ![]() and
and ![]() leads us to write
leads us to write ![]() .
.
Evaluating this gives the numerical approximation ![]() .
.
Example 5.4.3.4
Use an appropriate change of base formula to convert the following expressions to ones with the indicated base.
![]() to base
to base ![]()
Solution:
Convert ![]() to an equivalent expression base
to an equivalent expression base ![]() .
.
We write ![]() .
.
What Theorem 5.9 really tells us is that all exponential and logarithmic functions are just scalings of one another. Not only does this explain why their graphs have similar shapes, but it also tells us that we could do all of mathematics with a single base, be it 10, 0.42, ![]() , or 117.
, or 117.
5.4.1. Section Exercises
In Exercises 1 – 15, expand the given logarithm and simplify. Assume when necessary that all quantities represent positive real numbers.
In Exercises 16 – 29, use the properties of logarithms to write the expression as a single logarithm.
In Exercises 30 – 33, use the appropriate change of base formula to convert the given expression to an expression with the indicated base.
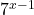 to base
to base 
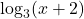 to base 10
to base 10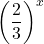 to base
to base 
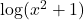 to base
to base 
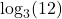
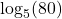
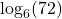
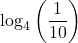
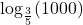
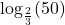
- In Example 5.3.1 number 3 in Section 5.3, we obtained the solution
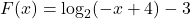 as one formula for the given graph by making a simplifying assumption that
as one formula for the given graph by making a simplifying assumption that 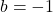 . This exercises explores if there are any other solutions for different choices of
. This exercises explores if there are any other solutions for different choices of  .
.
- Show
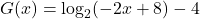 also fits the data for the given graph.
also fits the data for the given graph. - Use properties of logarithms to show
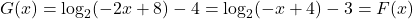 .
. - With help from your classmates, find solutions to Example 5.3.1 number 3 in Section 5.3 by assuming
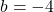 and
and 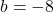 . In each case, use properties of logarithms to show the solutions reduce to
. In each case, use properties of logarithms to show the solutions reduce to 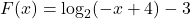 .
. - Using properties of logarithms and the fact that the range of
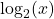 is all real numbers, show that any function of the form
is all real numbers, show that any function of the form 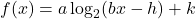 where
where 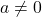 can be rewritten as:
can be rewritten as:
![Rendered by QuickLaTeX.com \[ f(x) = a \left( \log_{2}(bx-h) + \frac{k}{a}\right) = a ( \log_{2}(bx -h) + \log_{2}(p)) = a \log_{2}(p(bx-h)) = a \log_{2}(pbx - ph),\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-3006579ca4b5dc5966b355dee2f845a4_l3.png)
where
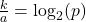 for some positive real number
for some positive real number 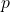 . Relabeling, we get every function of the form
. Relabeling, we get every function of the form 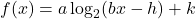 with four parameters (
with four parameters ( ,
,  ,
,  , and
, and 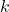 ) can be rewritten as
) can be rewritten as 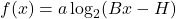 , a formula with just three parameters:
, a formula with just three parameters:  ,
, 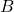 , and
, and 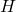 .Show every solution to Example 5.3.1 number 3 in Section 5.3 can be written in the form
.Show every solution to Example 5.3.1 number 3 in Section 5.3 can be written in the form 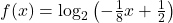 and that, in particular,
and that, in particular, 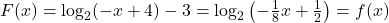 . Hence, there is really just one solution to Example 5.3.1 number 3 in Section 5.3.
. Hence, there is really just one solution to Example 5.3.1 number 3 in Section 5.3.
- Show
- The Henderson-Hasselbalch Equation: Suppose
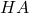 represents a weak acid. Then we have a reversible chemical reaction
represents a weak acid. Then we have a reversible chemical reaction
![Rendered by QuickLaTeX.com \[HA \rightleftharpoons H^{+} + A^{-}.\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b1e7903c9b41e23252c8bb25e80a0801_l3.png)
The acid disassociation constant,
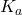 , is given by
, is given by![Rendered by QuickLaTeX.com \[K_{a} = \frac{[H^{+}][A^{-}]}{[HA]} = [H^{+}]\frac{[A^{-}]}{[HA]},\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9c8584bbe8d70fe5f04ec80614dcdab8_l3.png)
where the square brackets denote the concentrations just as they did in Exercise 83 in Section 5.3. The symbol p
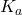 is defined similarly to pH in that p
is defined similarly to pH in that p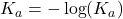 . Using the definition of pH from Exercise 83 and the properties of logarithms, derive the Henderson-Hasselbalch Equation:
. Using the definition of pH from Exercise 83 and the properties of logarithms, derive the Henderson-Hasselbalch Equation:![Rendered by QuickLaTeX.com \[\mbox{pH} = \mbox{p}K_{a} + \log\dfrac{[A^{-}]}{[HA]}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c53cd8778f9ae85856d5565fc4af26e5_l3.png)
- Compare and contrast the graphs of
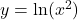 and
and 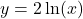 .
. - Prove the Quotient Rule and Power Rule for Logarithms.
- Give numerical examples to show that, in general,
- Research the history of logarithms including the origin of the word `logarithm’ itself. Why is the abbreviation of natural log `ln’ and not `nl’?
- There is a scene in the movie `Apollo 13′ in which several people at Mission Control use slide rules to verify a computation. Was that scene accurate? Look for other pop culture references to logarithms and slide rules.
Section 5.4 Exercise Answers can be found in the Appendix … Coming soon
- Interestingly enough, it is the exact opposite process (which we will practice later) that is most useful in Algebra, the utility of expanding logarithms becomes apparent in Calculus. ↵
- At this point in the text, the reader is encouraged to carefully read through each step and think of which quantity is playing the role of
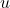 and which is playing the role of
and which is playing the role of 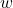 as we apply each property. ↵
as we apply each property. ↵ - We leave it to the reader to verify the domain of
 is
is 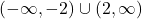 whereas the domain of
whereas the domain of  is
is 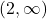 . ↵
. ↵ - The authors relish the irony involved in writing what follows. ↵

![Rendered by QuickLaTeX.com \log_{\frac{1}{2}}\left(\dfrac{4\sqrt[3]{x^2}}{y\sqrt{z}}\right)](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-568cb2126ac33609ed13a946b7ee9a05_l3.png)
