5.5 Solving Equations Involving Exponential Functions
In this section we will develop techniques for solving equations involving exponential functions. Consider the equation ![]() . After a moment’s calculation, we find
. After a moment’s calculation, we find ![]() , so we have
, so we have ![]() . The one-to-one property of exponential functions, detailed in Theorem 5.7, tells us that
. The one-to-one property of exponential functions, detailed in Theorem 5.7, tells us that ![]() if and only if
if and only if ![]() . This means that not only is
. This means that not only is ![]() a solution to
a solution to ![]() , it is the only solution.
, it is the only solution.
Now suppose we change the problem ever so slightly to ![]() . We could use one of the inverse properties of exponentials and logarithms listed in Theorem 5.6 to write
. We could use one of the inverse properties of exponentials and logarithms listed in Theorem 5.6 to write ![]() . We’d then have
. We’d then have ![]() , which means our solution is
, which means our solution is ![]() .
.
After all, the definition of ![]() is `the exponent we put on
is `the exponent we put on ![]() to get
to get ![]() .’ Indeed we could have obtained this solution directly by rewriting the equation
.’ Indeed we could have obtained this solution directly by rewriting the equation ![]() in its logarithmic form
in its logarithmic form ![]() . Either way, in order to get a reasonable decimal approximation to this number, we’d use the change of base formula, Theorem 5.9, to give us something more calculator friendly. Typically this means we convert our answer to base 10 or base
. Either way, in order to get a reasonable decimal approximation to this number, we’d use the change of base formula, Theorem 5.9, to give us something more calculator friendly. Typically this means we convert our answer to base 10 or base ![]() , and we choose the latter:
, and we choose the latter: ![]() .
.
Still another way to obtain this answer is to `take the natural log’ of both sides of the equation. Due to the fact that ![]() is a function, as long as two quantities are equal, their natural logs are equal.[1]
is a function, as long as two quantities are equal, their natural logs are equal.[1]
We then use the Power Rule to write the exponent ![]() as a factor then divide both sides by the constant
as a factor then divide both sides by the constant ![]() to obtain our answer.[2]
to obtain our answer.[2]
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 2^{x} & = & 129 & \\ \ln\left(2^{x}\right) & = & \ln(129) & \text{Take the natural log of both sides.} \\ x \ln(2) & = & \ln(129) & \text{Power Rule} \\ [4pt] x & = &\dfrac{\ln(129)}{\ln(2)} & \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5836b019399131a400eede624817b5a2_l3.png)
We summarize our two strategies for solving equations featuring exponential functions below.
Steps for Solving an Equation Involving Exponential Functions
- Isolate the exponential function.
- (a) If convenient, express both sides with a common base and equate the exponents.
(b) Otherwise, take the natural log of both sides of the equation and use the Power Rule.
Example 5.5.1
Example 5.5.1.1
Solve the following equations. Check your answer using a graphing utility.
![]()
Solution:
Solve ![]() for
for ![]() .
.
![]() is a power of
is a power of ![]() , so we can rewrite
, so we can rewrite ![]() as
as ![]() . Using properties of exponents, we get
. Using properties of exponents, we get ![]() .
.
Using the one-to-one property of exponential functions, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} 3x & = & 4(1-x) \\ 3x & = & 4 - 4x \\ 7x & = & 4 \\[4pt] x & = & \frac{4}{7} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-de996f9b9bbf6ab0e8554e5f5dc87405_l3.png)
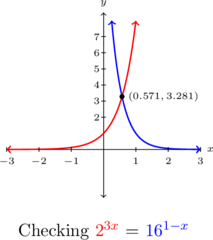
Graphing ![]() and
and ![]() and see that they intersect at
and see that they intersect at ![]() .
.
Example 5.5.1.2
Solve the following equations. Check your answer using a graphing utility.
![]()
Solution:
Solve ![]() for
for ![]() .
.
We begin solving ![]() by dividing both sides by
by dividing both sides by ![]() to isolate the exponential which yields
to isolate the exponential which yields ![]() .
.
As it is inconvenient to write ![]() as a power of
as a power of ![]() , we use the natural log to get
, we use the natural log to get
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \ln\left(3^{-0.1t}\right) & = & \ln(2) & \\ -0.1 t \ln(3) & = & \ln(2) & \text{Power Rule} \\[4pt] t & = & -\frac{\ln(2)}{0.1 \ln(3)} & \\[6pt] & = & -\frac{10\ln(2)}{\ln(3)} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-dff8fdf2e6728757b1eb05105de6c43a_l3.png)
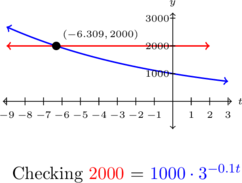
We see the graphs of ![]() and
and ![]() intersect at
intersect at ![]() .
.
Example 5.5.1.3
Solve the following equations. Check your answer using a graphing utility.
![]()
Solution:
Solve ![]() for
for ![]() .
.
We first note that we can rewrite the equation ![]() as
as ![]() to obtain
to obtain ![]() .
.
As it is not convenient to express both sides as a power of ![]() (or
(or ![]() for that matter) we use the natural log:
for that matter) we use the natural log: ![]() .
.
The power rule gives ![]() . Even though this equation appears very complicated, keep in mind that
. Even though this equation appears very complicated, keep in mind that ![]() and
and ![]() are just constants.
are just constants.
The equation ![]() is actually a linear equation (do you see why?) and as such we gather all of the terms with
is actually a linear equation (do you see why?) and as such we gather all of the terms with ![]() on one side, and the constants on the other. We then divide both sides by the coefficient of
on one side, and the constants on the other. We then divide both sides by the coefficient of ![]() , which we obtain by factoring.
, which we obtain by factoring.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} (x+2) \ln(3) & = & 2x \ln(7) & \\ x \ln(3) + 2 \ln(3) & = & 2x \ln(7) & \\ 2 \ln(3) & = & 2x \ln(7) - x \ln(3) & \\ 2 \ln(3) & = & x (2 \ln(7) - \ln(3)) & \text{Factor.}\\[4pt] x & = & \frac{2 \ln(3)}{2\ln(7) - \ln(3)} & \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9f8989c03e488680612167dfc461c5d4_l3.png)
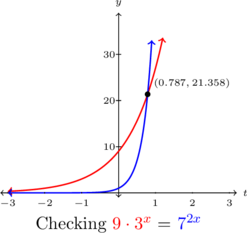
We see the graphs of ![]() and
and ![]() intersect at
intersect at ![]() .
.
Example 5.5.1.4
Solve the following equations. Check your answer using a graphing utility.
![]()
Solution:
Solve ![]() for
for ![]() .
.
Our objective in solving ![]() is to first isolate the exponential.
is to first isolate the exponential.
To that end, we clear denominators and get ![]() , or
, or
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 75 + 225e^{-2t} & = & 100 & \\ 225e^{-2t} & = & 25 & \\[4pt] e^{-2t} & = & \frac{1}{9} & \\[4pt] \ln\left(e^{-2t}\right) & = & \ln\left( \frac{1}{9} \right) & \text{Apply the natural log} \\[4pt] -2t & = & -\ln(9) & \text{Power Rule} \\ t & = & \frac{\ln(9)}{2} & \\[4pt] t & = & \ln(3) & \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-82ee1bf28fbd71377ee4eaac4ed5ea4b_l3.png)
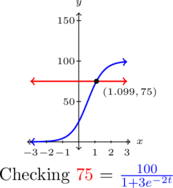
To check, we see the graphs of ![]() and
and ![]() , intersect at
, intersect at ![]() .
.
Example 5.5.1.5
Solve the following equations. Check your answer using a graphing utility.
![]()
Solution:
Solve ![]() for
for ![]() .
.
We start solving ![]() by rewriting
by rewriting ![]() so that we have
so that we have ![]() , or
, or ![]() .
.
Even though we have a common base, having two terms on the right hand side of the equation foils our plan of equating exponents or taking logs.
If we stare at this long enough, we notice that we have three terms with the exponent on one term exactly twice that of another. To our surprise and delight, we have a `quadratic in disguise’.
Letting ![]() , we have
, we have ![]() so the equation
so the equation ![]() becomes
becomes ![]() . Solving this as
. Solving this as ![]() gives
gives ![]() or
or ![]() . As
. As ![]() , we have
, we have
![]()
![]() has no real solution,[3] so we focus on
has no real solution,[3] so we focus on ![]() . It isn’t convenient to express
. It isn’t convenient to express ![]() as a power of
as a power of ![]() , thus we take natural logs and get
, thus we take natural logs and get ![]() so that
so that
![]()
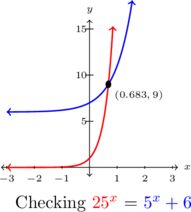
We see the graphs of ![]() and
and ![]() intersect at
intersect at ![]() .
.
Example 5.5.1.6
Solve the following equations. Check your answer using a graphing utility.
![]()
Solution:
Solve ![]() for
for ![]() .
.
Clearing the denominator in ![]() gives
gives ![]() , at which point we pause to consider how to proceed. Rewriting
, at which point we pause to consider how to proceed. Rewriting ![]() , we see we have another denominator to clear:
, we see we have another denominator to clear: ![]() .
.
Doing so gives ![]() , which, once again fits the criteria of being a `quadratic in disguise.’
, which, once again fits the criteria of being a `quadratic in disguise.’
If we let ![]() , then
, then ![]() so the equation
so the equation ![]() can be viewed as
can be viewed as ![]() . Solving
. Solving ![]() using the quadratic formula gives
using the quadratic formula gives ![]() .
.
From this, we have ![]() . Because
. Because ![]() , we get no real solution to
, we get no real solution to ![]() (why not?) but for
(why not?) but for ![]() , we take natural logs to obtain
, we take natural logs to obtain ![]() .
.
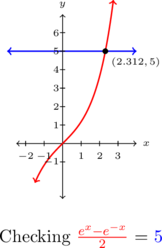
We see the graphs of ![]() and
and ![]() intersect at
intersect at ![]() .
.
Note that verifying our solutions to the equations in Example 5.5.1 analytically holds great educational value, as it reviews many of the properties of logarithms and exponents in tandem.
For example, to verify our solution to ![]() , we substitute
, we substitute ![]() and check:
and check:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 2000 & \stackrel{?}{=} & 1000 \cdot 3^{-0.1 \left(-\frac{10\ln(2)}{\ln(3)}\right)} & \\ 2000 & \stackrel{?}{=} & 1000 \cdot 3^{\frac{\ln(2)}{\ln(3)}} & \\ 2000 & \stackrel{?}{=} & 1000 \cdot 3^{\log_{3}(2)} & \text{Change of Base}\\ 2000 & \stackrel{?}{=} & 1000 \cdot 2 & \text{Inverse Property}\\ 2000 & \stackrel{\checkmark}{=} & 2000 & \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-73434f26a3575fcfa46b2ef23b3d8b17_l3.png)
We strongly encourage the reader to check the remaining equations analytically as well.
We close this section by finding a function inverse.
Example 5.5.2
Example 5.5.2.1
The function ![]() is one-to-one.
is one-to-one.
Write a formula for ![]() .
.
Solution:
Write a formula for ![]() .
.
We start by writing ![]() , and interchange the roles of
, and interchange the roles of ![]() and
and ![]() . To solve for
. To solve for ![]() , we first clear denominators and then isolate the exponential function.
, we first clear denominators and then isolate the exponential function.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} y & = & \dfrac{5e^{x}}{e^{x}+1} & \\ [12pt] x & = & \dfrac{5e^{y}}{e^{y}+1} & \text{Switch } x \text{ and } y \\ [12pt] x \left(e^{y}+1\right) & = & 5e^{y} & \\ [4pt] x e^{y}+x & = & 5e^{y} & \\ [4pt] x & = & 5e^{y} - x e^{y} & \\ [4pt] x & = & e^{y}(5 - x) & \\ [4pt] e^{y}& = & \dfrac{x}{5-x} & \\[12pt] \ln\left(e^{y}\right) & = & \ln\left(\dfrac{x}{5-x}\right) & \\[12pt] y & = & \ln\left(\dfrac{x}{5-x}\right) & \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c6a2fff102c4fbbc720b71c36ee30e7a_l3.png)
We claim ![]() . To verify this analytically, we would need to verify the compositions
. To verify this analytically, we would need to verify the compositions ![]() for all
for all ![]() in the domain of
in the domain of ![]() and that
and that ![]() for all
for all ![]() in the domain of
in the domain of ![]() . We leave this, as well as a graphical check, to the reader in Exercise 41.
. We leave this, as well as a graphical check, to the reader in Exercise 41.
Example 5.5.2.2
The function ![]() is one-to-one.
is one-to-one.
Solve ![]() .
.
Solution:
Solve ![]() .
.
We recognize the equation ![]() as
as ![]() . Hence, our solution is
. Hence, our solution is
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} x &=& f^{-1}(4) \\[4pt] &=& \ln\left(\frac{4}{5-4}\right) \\[4pt] &=& \ln(4) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a0241044f93c95492237b60d85072019_l3.png)
We can check this fairly quickly algebraically. Using ![]() , we find
, we find ![]() .
.
5.5.1 Section Exercises
In Exercises 1 – 33, solve the equation analytically.
In Exercises 34 – 39, find the domain of the function
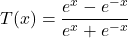
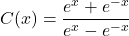
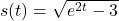
![Rendered by QuickLaTeX.com c(t) = \sqrt[3]{e^{2t} - 3}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-55fca1c5a52eadf23f894154260fc0ab_l3.png)
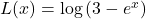
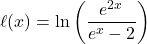
- Compute the inverse of
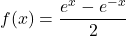 . State the domain and range of both
. State the domain and range of both  and
and 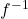 .
. - In Example 5.5.1, we found that the inverse of
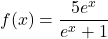 was
was 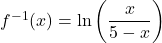 but we left a few loose ends for you to tie up.
but we left a few loose ends for you to tie up.
- Algebraically check our answer by verifying:
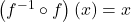 for all
for all  in the domain of
in the domain of  and that
and that 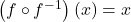 for all
for all  in the domain of
in the domain of 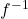 .
. - Find the range of
 by finding the domain of
by finding the domain of 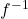 .
. - With help of a graphing utility, graph
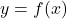 ,
, 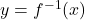 and
and 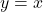 on the same set of axes. How does this help to verify our answer?
on the same set of axes. How does this help to verify our answer? - Let
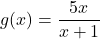 and
and 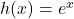 . Show that
. Show that 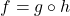 and that
and that 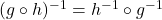 .
.
- Algebraically check our answer by verifying:
Section 5.5 Exercise Answers can be found in the Appendix … Coming soon

