7.2 Sine and Cosine Functions
7.2.1 Right Triangle Definitions
This section focuses on right triangles, triangles in which one angle measures ![]() . Consider the right triangle below, where, as usual, the small square
. Consider the right triangle below, where, as usual, the small square ![]() denotes the right angle, the labels `
denotes the right angle, the labels `![]() ,’ `
,’ `![]() ,’ and `
,’ and `![]() ‘ denote the lengths of the sides of the triangle, and
‘ denote the lengths of the sides of the triangle, and ![]() and
and ![]() represent the (measure of) the non-right angles. As you may recall, the side opposite the right angle is called the hypotenuse of the right triangle. Also note that because the sum of the measures of all angles in a triangle must add to
represent the (measure of) the non-right angles. As you may recall, the side opposite the right angle is called the hypotenuse of the right triangle. Also note that because the sum of the measures of all angles in a triangle must add to ![]() , we have
, we have ![]() , or
, or ![]() . Said differently, the non-right angles in a right triangle are complements.
. Said differently, the non-right angles in a right triangle are complements.

We now state and prove the most famous result about right triangles: The Pythagorean Theorem.
Theorem 7.1 The Pythagorean Theorem
The square of the length of the hypotenuse of a right triangle is equal to the sums of the squares of the other two sides.
More specifically, if ![]() is the length of the hypotenuse of a right triangle and
is the length of the hypotenuse of a right triangle and ![]() and
and ![]() are the lengths of the other two sides, then
are the lengths of the other two sides, then ![]() .
.
There are several proofs of the Pythagorean Theorem,[1] but the one we choose to reproduce here showcases a nice interplay between algebra and geometry. Consider taking four copies of the right triangle below on the left and arranging them as seen below on the right.
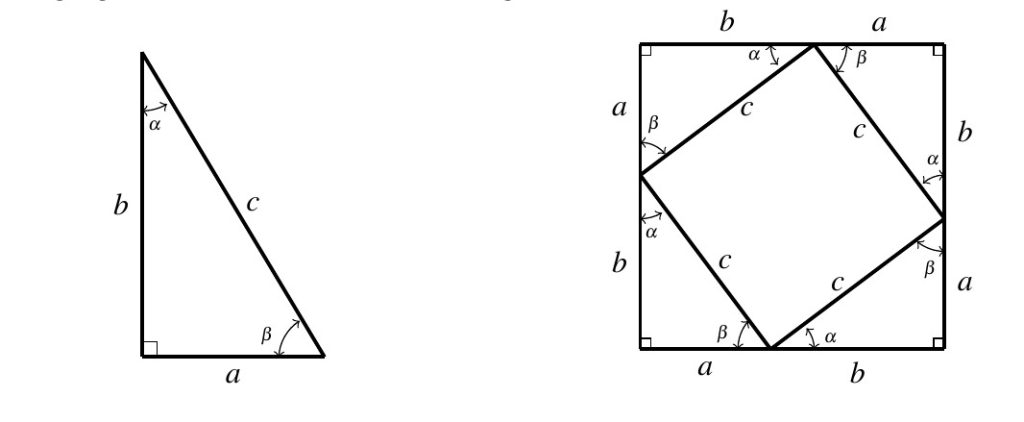
It should be clear that we have produced a large square with a side length of ![]() . What is also true, but may not be obvious, is that the inner quadrilateral is also a square. We can readily see the inner quadrilateral has equal sides of length
. What is also true, but may not be obvious, is that the inner quadrilateral is also a square. We can readily see the inner quadrilateral has equal sides of length ![]() . Moreover, because
. Moreover, because ![]() , we get the interior angles of the inner quadrilateral are each
, we get the interior angles of the inner quadrilateral are each ![]() . Hence, the inner quadrilateral is indeed a square.
. Hence, the inner quadrilateral is indeed a square.
We finish the proof by computing the area of the large square in two ways. First, we square the length of its side: ![]() . Next, we add up the areas of the four triangles, each having area
. Next, we add up the areas of the four triangles, each having area ![]() along with the area of the inner square,
along with the area of the inner square, ![]() . Equating these to expressions gives:
. Equating these to expressions gives: ![]() . As a result of
. As a result of ![]() and
and ![]() , we have
, we have ![]() or
or ![]() , as required.
, as required.
It should be noted that the converse of the Pythagorean Theorem is also true. That is if ![]() ,
, ![]() , and
, and ![]() are the lengths of sides of a triangle and
are the lengths of sides of a triangle and ![]() , then the triangle is a right triangle.[2]
, then the triangle is a right triangle.[2]
A list of integers ![]() which satisfy the relationship
which satisfy the relationship ![]() is called a Pythagorean Triple. Some of the more common triples are:
is called a Pythagorean Triple. Some of the more common triples are: ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . We leave it to the reader to verify these integers satisfy the equation
. We leave it to the reader to verify these integers satisfy the equation ![]() and suggest committing these triples to memory.
and suggest committing these triples to memory.
Next, we set about defining characteristic ratios associated with acute angles. Given any acute angle ![]() , we can imagine
, we can imagine ![]() being an interior angle of a right triangle as seen below.
being an interior angle of a right triangle as seen below.
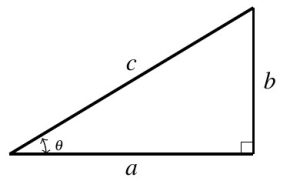
Focusing on the arrangement of the sides of the triangle with respect to the angle ![]() , we make the following definitions: the side with length
, we make the following definitions: the side with length ![]() is called the side of the triangle which is adjacent to
is called the side of the triangle which is adjacent to ![]() and the side with length
and the side with length ![]() is called the side of the triangle opposite
is called the side of the triangle opposite ![]() . As usual, the side labeled `
. As usual, the side labeled `![]() ‘ (the side opposite the right angle) is the hypotenuse. Using this diagram, we define two important trigonometric ratios of
‘ (the side opposite the right angle) is the hypotenuse. Using this diagram, we define two important trigonometric ratios of ![]() .
.
Definition 7.2
Suppose ![]() is an acute angle residing in a right triangle as depicted above.
is an acute angle residing in a right triangle as depicted above.
- The sine of
 , denoted
, denoted 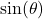 is defined by the ratio:
is defined by the ratio: 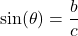 , or
, or 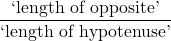 .
. - The cosine of
 , denoted
, denoted 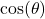 is defined by the ratio:
is defined by the ratio: 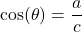 , or
, or 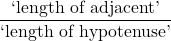 .
.
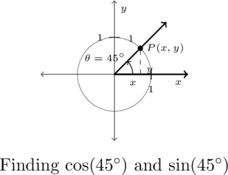
For example, consider the angle ![]() indicated in the 3-4-5 triangle given. Using Definition 7.2, we get
indicated in the 3-4-5 triangle given. Using Definition 7.2, we get ![]() and
and ![]() . One may well wonder if these trigonometric ratios we’ve found for
. One may well wonder if these trigonometric ratios we’ve found for ![]() change if the triangle containing
change if the triangle containing ![]() changes. For example, if we scale all the sides of the 3-4-5 triangle on the left by a factor of
changes. For example, if we scale all the sides of the 3-4-5 triangle on the left by a factor of ![]() , we produce the similar triangle below in the middle.[3] Using this triangle to compute our ratios for
, we produce the similar triangle below in the middle.[3] Using this triangle to compute our ratios for ![]() , we find
, we find ![]() and
and ![]() . Note that the scaling factor, here
. Note that the scaling factor, here ![]() , is common to all sides of the triangle, and, hence, divides out of the numerator and denominator when simplifying each of the ratios.
, is common to all sides of the triangle, and, hence, divides out of the numerator and denominator when simplifying each of the ratios.
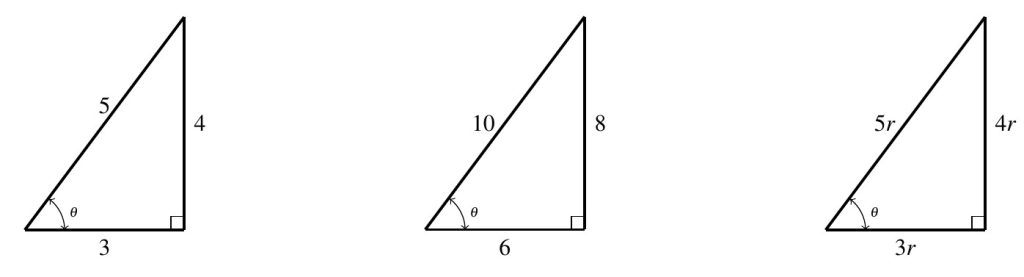
In general, thanks to the Angle Angle Similarity Postulate, any two right triangles which contain our angle ![]() are similar which means there is a positive constant
are similar which means there is a positive constant ![]() so that the sides of the triangle are
so that the sides of the triangle are ![]() ,
, ![]() , and
, and ![]() as seen above on the right. Hence, regardless of the right triangle in which we choose to imagine
as seen above on the right. Hence, regardless of the right triangle in which we choose to imagine ![]() ,
, ![]() and
and ![]() . Generalizing this same argument to any acute angle
. Generalizing this same argument to any acute angle ![]() assures us that the ratios as described in Definition 7.2 are independent of the triangle we use.
assures us that the ratios as described in Definition 7.2 are independent of the triangle we use.
Our next objective is to determine the values of ![]() and
and ![]() for some of the more commonly used angles. We begin with
for some of the more commonly used angles. We begin with ![]() . In a right triangle, if one of the non-right angles measures
. In a right triangle, if one of the non-right angles measures ![]() , then the other measures
, then the other measures ![]() as well. It follows that the two legs of the triangle must be congruent. We may choose any right triangle containing a
as well. It follows that the two legs of the triangle must be congruent. We may choose any right triangle containing a ![]() angle for our computations, thus we choose the length of one (hence both) of the legs to be
angle for our computations, thus we choose the length of one (hence both) of the legs to be ![]() . The Pythagorean Theorem gives the hypotenuse is:
. The Pythagorean Theorem gives the hypotenuse is: ![]() , so
, so ![]() . (We take only the positive square root here as
. (We take only the positive square root here as ![]() represents the length of the hypotenuse here, so, necessarily
represents the length of the hypotenuse here, so, necessarily ![]() .) From this, we obtain the values below, and suggest committing them to memory.
.) From this, we obtain the values below, and suggest committing them to memory.
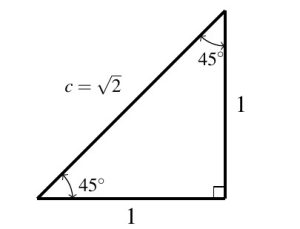
Note that we have `rationalized’ here to avoid the irrational number ![]() appearing in the denominator. This is a common convention in trigonometry, and we will adhere to it unless extremely inconvenient.
appearing in the denominator. This is a common convention in trigonometry, and we will adhere to it unless extremely inconvenient.
Next, we investigate ![]() and
and ![]() angles. Consider the equilateral triangle each of whose sides measures
angles. Consider the equilateral triangle each of whose sides measures ![]() units. Each of its interior angles is necessarily
units. Each of its interior angles is necessarily ![]() , so if we drop an altitude, we produce two
, so if we drop an altitude, we produce two ![]() triangles each having a base measuring
triangles each having a base measuring ![]() unit and a hypotenuse of
unit and a hypotenuse of ![]() units. Using the Pythagorean Theorem, we can find the height,
units. Using the Pythagorean Theorem, we can find the height, ![]() of these triangles:
of these triangles: ![]() so
so ![]() or
or ![]() . Using these, we can find the values of the trigonometric ratios for both
. Using these, we can find the values of the trigonometric ratios for both ![]() and
and ![]() . Again, we recommend committing these values to memory.
. Again, we recommend committing these values to memory.
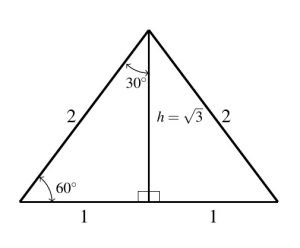
Sine Values:
Cosine Values:
Recall ![]() and
and ![]() are complements, so the side adjacent to the
are complements, so the side adjacent to the ![]() angle is the side opposite the
angle is the side opposite the ![]() and the side opposite the
and the side opposite the ![]() angle is the side adjacent to the
angle is the side adjacent to the ![]() . This sort of `swapping’ is true of all complementary angles and will be generalized in Section 8.2, Theorem 8.6.
. This sort of `swapping’ is true of all complementary angles and will be generalized in Section 8.2, Theorem 8.6.
Note that the values of the trigonometric ratios we have derived for ![]() ,
, ![]() , and
, and ![]() angles are the exact values of these ratios. For these angles, we can conveniently express the exact values of their sines and cosines resorting, at worst, to using square roots. The reader may well wonder if, for instance, we can express the exact value of, say,
angles are the exact values of these ratios. For these angles, we can conveniently express the exact values of their sines and cosines resorting, at worst, to using square roots. The reader may well wonder if, for instance, we can express the exact value of, say, ![]() in terms of radicals. The answer in this case is `yes’ (see here), but, in general, we will not take the time to pursue such representations.[4] Hence, if a problem requests an `exact’ answer involving
in terms of radicals. The answer in this case is `yes’ (see here), but, in general, we will not take the time to pursue such representations.[4] Hence, if a problem requests an `exact’ answer involving ![]() , we will leave it written as `
, we will leave it written as `![]() ‘ and use a calculator to produce a suitable approximation as the situation warrants.
‘ and use a calculator to produce a suitable approximation as the situation warrants.
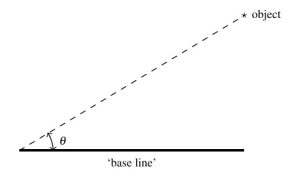
The angle of inclination (or angle of elevation) of an object refers to the angle whose initial side is some kind of base-line (say, the ground), and whose terminal side is the line-of-sight to an object above the base-line. Schematically:
7.2.2 Unit Circle Definitions
In Section 7.1.3, we introduced circular motion and derived a formula which describes the linear velocity of an object moving on a circular path at a constant angular velocity. One of the goals of this section is describe the position of such an object. To that end, consider an angle ![]() in standard position and let
in standard position and let ![]() denote the point where the terminal side of
denote the point where the terminal side of ![]() intersects the Unit Circle, as diagrammed below.
intersects the Unit Circle, as diagrammed below.
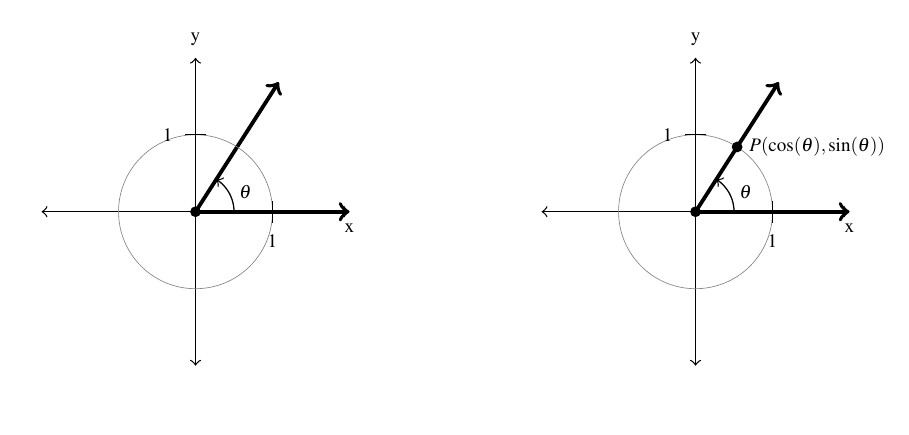
By associating the point ![]() with the angle
with the angle ![]() , we are assigning a position on the Unit Circle to the angle
, we are assigning a position on the Unit Circle to the angle ![]() . For each angle
. For each angle ![]() , the terminal side of
, the terminal side of ![]() , when graphed in standard position, intersects The Unit Circle only once, so the mapping of
, when graphed in standard position, intersects The Unit Circle only once, so the mapping of ![]() to
to ![]() is a function.[5] Because there is only one way to describe a point using rectangular coordinates,[6] the mappings of
is a function.[5] Because there is only one way to describe a point using rectangular coordinates,[6] the mappings of ![]() to each of the
to each of the ![]() and
and ![]() coordinates of
coordinates of ![]() are also functions. We give these functions names in the following definition.
are also functions. We give these functions names in the following definition.
Definition 7.3
Suppose an angle ![]() is graphed in standard position. Let
is graphed in standard position. Let ![]() be the point of intersection of the terminal side of
be the point of intersection of the terminal side of ![]() and the Unit Circle.
and the Unit Circle.
- The
 -coordinate of
-coordinate of  is called the cosine of
is called the cosine of  , written
, written  .
. - The
 -coordinate of
-coordinate of 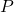 is called the sine of
is called the sine of  , written
, written 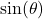 .[7]
.[7]
You may have already seen definitions for the sine and cosine of an (acute) angle in terms of ratios of sides of a right triangle.[8] While not incorrect, defining sine and cosine using right triangles limits the angles we can study to acute angles only. Definition 7.3, on the other hand, applies to all angles. These functions are defined in terms of points on the Unit Circle, thus they are called circular functions. Rest assured, Definition 7.3 specializes to Definition 7.2 when ![]() is an acute angle. We will see instances of this fact in the next example.
is an acute angle. We will see instances of this fact in the next example.
Example 7.2.1
Example 7.2.1.1
State the sine and cosine of the following angles.
![]()
Solution:
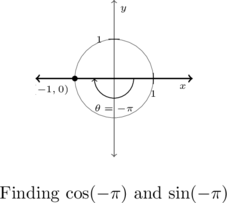
State the sine and cosine of ![]() .
.
To find ![]() and
and ![]() , we plot the angle
, we plot the angle ![]() in standard position and find the point on the terminal side of
in standard position and find the point on the terminal side of ![]() which lies on the Unit Circle. As
which lies on the Unit Circle. As ![]() represents
represents ![]() of a counter-clockwise revolution, the terminal side of
of a counter-clockwise revolution, the terminal side of ![]() lies along the negative
lies along the negative ![]() -axis.
-axis.
Hence, the point we seek is ![]() so that
so that ![]() and
and ![]() .
.
Example 7.2.1.2
State the sine and cosine of the following angles.
![]()
Solution:
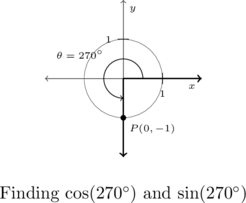
State the sine and cosine of ![]() .
.
The angle ![]() represents one half of a clockwise revolution so its terminal side lies on the negative
represents one half of a clockwise revolution so its terminal side lies on the negative ![]() -axis.
-axis.
The point on the Unit Circle that lies on the negative ![]() -axis is
-axis is ![]() which means
which means ![]() and
and ![]() .
.
Example 7.2.1.3
State the sine and cosine of the following angles.
![]()
Solution:
State the sine and cosine of ![]() .
.
In this section, we derived values for ![]() and
and ![]() using Definition 7.2. In order to connect what we know from Section 7.2.1 with what we are asked to find per Definition 7.3, we sketch
using Definition 7.2. In order to connect what we know from Section 7.2.1 with what we are asked to find per Definition 7.3, we sketch ![]() in standard position and let
in standard position and let ![]() denote the point on the terminal side of
denote the point on the terminal side of ![]() which lies on the Unit Circle. If we drop a perpendicular line segment from
which lies on the Unit Circle. If we drop a perpendicular line segment from ![]() to the
to the ![]() -axis as shown, we obtain a
-axis as shown, we obtain a ![]() right triangle whose legs have lengths
right triangle whose legs have lengths ![]() and
and ![]() units with hypotenuse
units with hypotenuse ![]() .
.
From our work in Section 7.2.1, we obtain the (familiar) values ![]() and
and ![]() .
.
Example 7.2.1.4
State the sine and cosine of the following angles.
![]()
Solution:
State the sine and cosine of ![]() .
.
As before, the terminal side of ![]() does not lie on any of the coordinate axes, so we proceed using a triangle approach. Letting
does not lie on any of the coordinate axes, so we proceed using a triangle approach. Letting ![]() denote the point on the terminal side of
denote the point on the terminal side of ![]() which lies on the Unit Circle, we drop a perpendicular line segment from
which lies on the Unit Circle, we drop a perpendicular line segment from ![]() to the
to the ![]() -axis to form a
-axis to form a ![]() right triangle.
right triangle.
Re-using some of our work from this section, we get ![]() and
and ![]() .
.
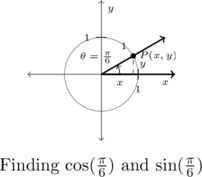
Example 7.2.1.5
State the sine and cosine of the following angles.
![]()
Solution:
State the sine and cosine of ![]() .
.
We plot ![]() in standard position below on the left and, as usual, let
in standard position below on the left and, as usual, let ![]() denote the point on the terminal side of
denote the point on the terminal side of ![]() which lies on the Unit Circle. In plotting
which lies on the Unit Circle. In plotting ![]() , we find it lies
, we find it lies ![]() radians short of one half revolution.
radians short of one half revolution.
As we’ve just determined that ![]() and
and ![]() , we know the coordinates of the point
, we know the coordinates of the point ![]() below on the right are
below on the right are ![]() .
.
Using symmetry, the coordinates of ![]() are
are ![]() , so
, so ![]() and
and ![]() .
.

A few remarks are in order. First, after having re-used some of our work from this section in a few specific instances, we can reconcile Definition 7.3 with Definition 7.2 in the case ![]() is an acute angle. We situate
is an acute angle. We situate ![]() in a right triangle with hypotenuse length
in a right triangle with hypotenuse length ![]() , adjacent side length `
, adjacent side length `![]() ,’ and the opposite side length `
,’ and the opposite side length `![]() ‘ as seen below on the left. Placing the vertex of
‘ as seen below on the left. Placing the vertex of ![]() at the origin and the adjacent side of
at the origin and the adjacent side of ![]() along the
along the ![]() -axis as seen below on the right effectively puts
-axis as seen below on the right effectively puts ![]() in standard position with
in standard position with ![]() ‘s adjacent side as the initial side of
‘s adjacent side as the initial side of ![]() and the hypotenuse as the terminal side of
and the hypotenuse as the terminal side of ![]() . The hypotenuse of the triangle has length
. The hypotenuse of the triangle has length ![]() , thus we know the point
, thus we know the point ![]() is on the Unit Circle.[9]
is on the Unit Circle.[9]

Definition 7.2 gives ![]() and
and ![]() which exactly matches Definition 7.3. Hence, in the case of acute angles, the two definitions agree. In other words, the values of the trigonometric ratios} of acute angles are the same as the corresponding circular function values.
which exactly matches Definition 7.3. Hence, in the case of acute angles, the two definitions agree. In other words, the values of the trigonometric ratios} of acute angles are the same as the corresponding circular function values.
A second important take-away from Example 7.2.1 is use of symmetry in number 5. Indeed, we found the sine and cosine of ![]() using the (acute) angle
using the (acute) angle ![]() `for reference.’ As the Unit Circle is rife with symmetry, we would like to generalize this concept and exploit symmetry whenever possible. To that end, we introduce the notion of reference angle.
`for reference.’ As the Unit Circle is rife with symmetry, we would like to generalize this concept and exploit symmetry whenever possible. To that end, we introduce the notion of reference angle.
In general, for a non-quadrantal angle ![]() , the reference angle for
, the reference angle for ![]() (which we’ll usually denote
(which we’ll usually denote ![]() ) is the acute angle made between the terminal side of
) is the acute angle made between the terminal side of ![]() and the
and the ![]() -axis. If
-axis. If ![]() is a Quadrant I or IV angle,
is a Quadrant I or IV angle, ![]() is the angle between the terminal side of
is the angle between the terminal side of ![]() and the positive
and the positive ![]() -axis:
-axis:
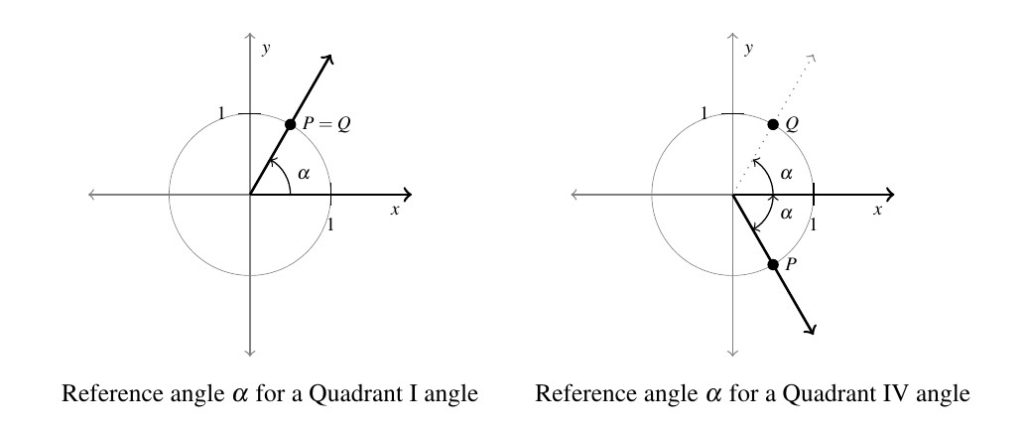
If ![]() is a Quadrant II or III angle,
is a Quadrant II or III angle, ![]() is the angle between the terminal side of
is the angle between the terminal side of ![]() and thenegative
and thenegative ![]() -axis:
-axis:
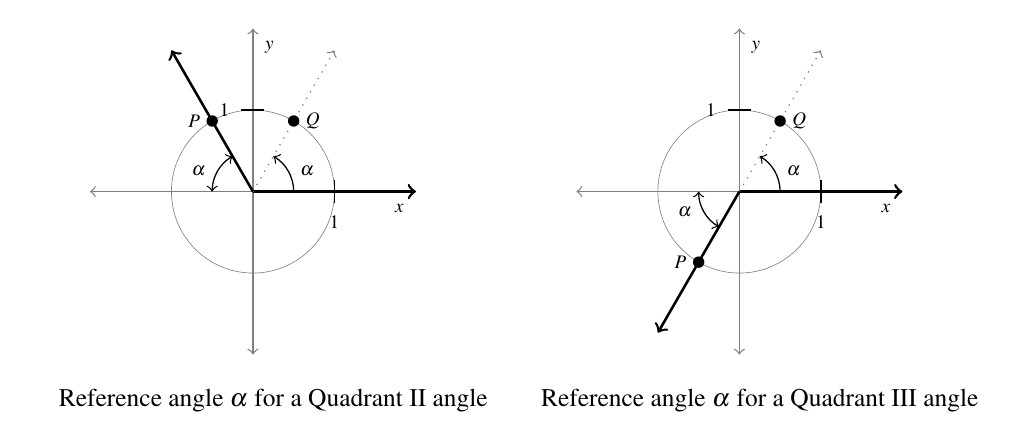
If we let ![]() denote the point
denote the point ![]() , then
, then ![]() lies on the Unit Circle. Due to the fact that the Unit Circle possesses symmetry with respect to the
lies on the Unit Circle. Due to the fact that the Unit Circle possesses symmetry with respect to the ![]() -axis,
-axis, ![]() -axis and origin, regardless of where the terminal side of
-axis and origin, regardless of where the terminal side of ![]() lies, there is a point
lies, there is a point ![]() symmetric with
symmetric with ![]() which determines
which determines ![]() ‘s reference angle,
‘s reference angle, ![]() . The only difference between the points
. The only difference between the points ![]() and
and ![]() are the signs of their coordinates,
are the signs of their coordinates, ![]() . Hence, we have the following:
. Hence, we have the following:
Theorem 7.2 Reference Angle Theorem
Suppose ![]() is the reference angle for
is the reference angle for ![]() . Then:
. Then:
![]()
where the choice of the (![]() ) depends on the quadrant in which the terminal side of
) depends on the quadrant in which the terminal side of ![]() lies.
lies.
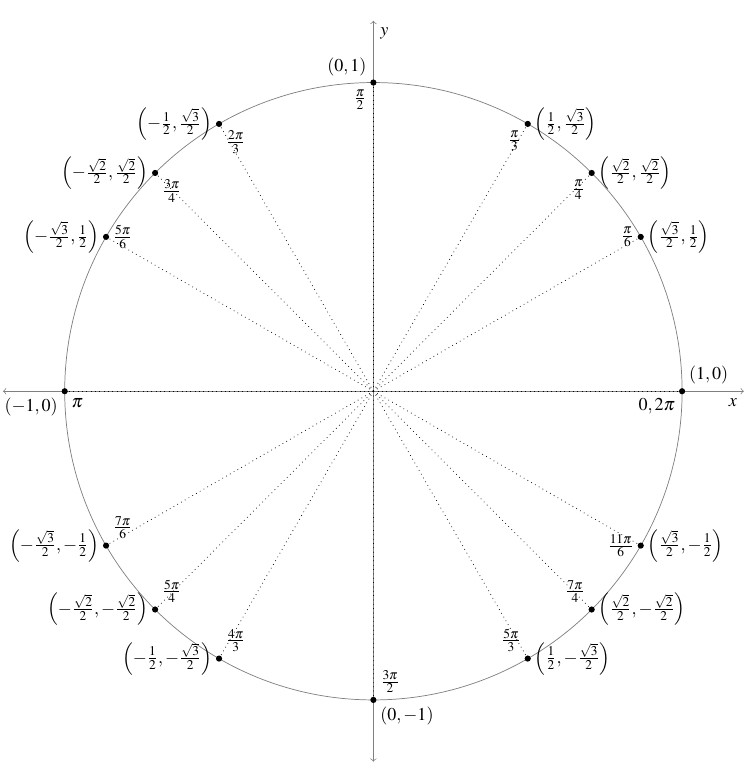
In light of Theorem 7.2, it pays to know the sine and cosine values for certain common Quadrant I angles as well as to keep in mind the signs of the coordinates of points in the given quadrants.
![Rendered by QuickLaTeX.com \[ \begin{array}{|c|c||c|c|} \hline \theta (\text{degrees}) & \theta (\text{radians}) & \cos(\theta) & \sin(\theta) \\ \hline 0^{\circ} & 0 & 1 & 0 \\ \hline 30^{\circ} & \frac{\pi}{6} & \frac{\sqrt{3}}{2} & \frac{1}{2} \\ [2pt] \hline 45^{\circ} & \frac{\pi}{4} & \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\ [2pt] \hline 60^{\circ} & \frac{\pi}{3} & \frac{1}{2} & \frac{\sqrt{3}}{2} \\ [2pt] \hline 90^{\circ} & \frac{\pi}{2} & 0 & 1 \\ [2pt] \hline \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-bbce27141f7a5fb69af663df88967f4c_l3.png)
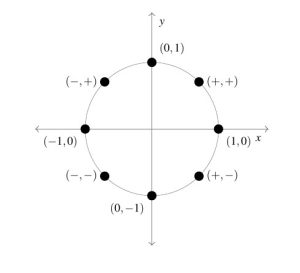
Example 7.2.2
Example 7.2.2.1
Determine the sine and cosine of the following angles.
![]()
Solution:
Determine the sine and cosine of ![]() .
.
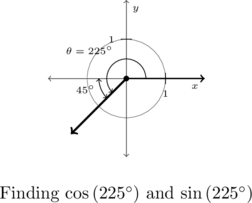
We begin by plotting ![]() in standard position and find its terminal side overshoots the negative
in standard position and find its terminal side overshoots the negative ![]() -axis to land in Quadrant III.
-axis to land in Quadrant III.
Hence, we obtain ![]() ‘s reference angle
‘s reference angle ![]() by subtracting:
by subtracting: ![]() .
.
As ![]() is a Quadrant III angle, both
is a Quadrant III angle, both ![]() and
and ![]() . The Reference Angle Theorem yields:
. The Reference Angle Theorem yields:
![]() and
and ![]()
Example 7.2.2.2
Determine the sine and cosine of the following angles.
![]()
Solution:
Determine the sine and cosine of ![]() .
.
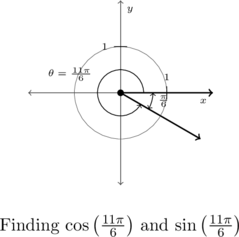
The terminal side of ![]() , when plotted in standard position, lies in Quadrant IV, just shy of the positive
, when plotted in standard position, lies in Quadrant IV, just shy of the positive ![]() -axis.
-axis.
To find ![]() ‘s reference angle
‘s reference angle ![]() , we subtract:
, we subtract: ![]() .
.
As ![]() is a Quadrant IV angle,
is a Quadrant IV angle, ![]() and
and ![]() , so the Reference Angle Theorem gives:
, so the Reference Angle Theorem gives:
![]() and
and ![]()
Example 7.2.2.3
Determine the sine and cosine of the following angles.
![]()
Solution:
Determine the sine and cosine of ![]() .
.
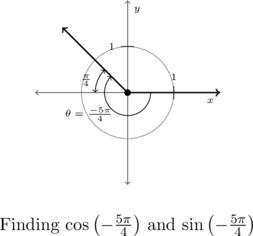
To plot ![]() , we rotate clockwise an angle of
, we rotate clockwise an angle of ![]() from the positive
from the positive ![]() -axis. The terminal side of
-axis. The terminal side of ![]() , therefore, lies in Quadrant II making an angle of
, therefore, lies in Quadrant II making an angle of ![]() radians with respect to the negative
radians with respect to the negative ![]() -axis.
-axis.
As ![]() is a Quadrant II angle,
is a Quadrant II angle, ![]() and
and ![]() so the Reference Angle Theorem gives:
so the Reference Angle Theorem gives:
![]() and
and ![]()
Example 7.2.2.4
Determine the sine and cosine of the following angles.
![]()
Solution:
Determine the sine and cosine of ![]() .
.
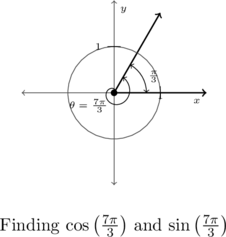
Given the angle ![]() measures more than
measures more than ![]() , we find the terminal side of
, we find the terminal side of ![]() by rotating one full revolution followed by an additional
by rotating one full revolution followed by an additional ![]() radians.
radians.
Hence, ![]() and
and ![]() have the same terminal side,[10] and so
have the same terminal side,[10] and so
![]() and
and ![]()
A couple of remarks are in order. First off, the reader may have noticed that when expressed in radian measure, the reference angle for a non-quadrantal angle is easy to spot. Reduced fraction multiples of ![]() with a denominator of
with a denominator of ![]() have
have ![]() as a reference angle, those with a denominator of
as a reference angle, those with a denominator of ![]() have
have ![]() as their reference angle, and those with a denominator of
as their reference angle, and those with a denominator of ![]() have
have ![]() as their reference angle.[11]
as their reference angle.[11]
Also note in number 4 of the last example, the angles ![]() and
and ![]() are coterminal. As a result, have the same values for sine and cosine. It turns out that we can characterize coterminal angles in this manner, as stated below.
are coterminal. As a result, have the same values for sine and cosine. It turns out that we can characterize coterminal angles in this manner, as stated below.
Recall the phraseology `if and only if’ means there are two things to argue in Theorem 7.3: first, if ![]() and
and ![]() are co-terminal, then
are co-terminal, then ![]() and
and ![]() . This is immediate as coterminal share terminal sides, and, in particular, the (unique) point on the Unit Circle shared by said terminal side. Second, we need to argue that if
. This is immediate as coterminal share terminal sides, and, in particular, the (unique) point on the Unit Circle shared by said terminal side. Second, we need to argue that if ![]() and
and ![]() , then
, then ![]() and
and ![]() are coterminal.
are coterminal.
To prove this second claim, note that when an angle is drawn in standard position, the terminal side of the angle is the ray that starts at the origin and is completely determined by any other point on the terminal side. If ![]() and
and ![]() , then their terminal sides share a point on the Unit Circle, namely
, then their terminal sides share a point on the Unit Circle, namely ![]() . Hence,
. Hence, ![]() and
and ![]() are coterminal.
are coterminal.
The Reference Angle Theorem in conjunction with the table of sine and cosine values given previously can be used to generate the figure below. We recommend committing it to memory.
Example 7.2.3
Example 7.2.3.1
Suppose ![]() is an acute angle with
is an acute angle with ![]() .
.
Determine ![]() and use this to plot
and use this to plot ![]() in standard position.
in standard position.
Solution:
Suppose ![]() is an acute angle with
is an acute angle with ![]() . Determine
. Determine ![]() and use this to plot
and use this to plot ![]() in standard position.
in standard position.
Given ![]() is an acute angle, we know
is an acute angle, we know ![]() , so the terminal side of
, so the terminal side of ![]() lies in Quadrant I.
lies in Quadrant I.
Moreover, because ![]() , we know the
, we know the ![]() -coordinate of the intersection point of the terminal side of
-coordinate of the intersection point of the terminal side of ![]() and the Unit Circle is
and the Unit Circle is ![]() .
.
To find ![]() , we need the
, we need the ![]() -coordinate. Taking a cue from Example 7.2.1, we drop a perpendicular from the terminal side of
-coordinate. Taking a cue from Example 7.2.1, we drop a perpendicular from the terminal side of ![]() to the
to the ![]() -axis as seen below on the right to form a right triangle with one leg measuring
-axis as seen below on the right to form a right triangle with one leg measuring ![]() units and hypotenuse with a length of
units and hypotenuse with a length of ![]() unit.
unit.
The Pythagorean Theorem gives ![]() or
or ![]() .
.
Hence, ![]() .
.

Example 7.2.3.2a
Suppose ![]() is an acute angle with
is an acute angle with ![]() .
.
State the sine and cosine of the following angles:
![]()
Solution:
State the sine and cosine of ![]() .
.
To find the cosine and sine of ![]() , we first plot
, we first plot ![]() in standard position.
in standard position.
We can imagine the sum of the angles ![]() as a sequence of two rotations: a rotation of
as a sequence of two rotations: a rotation of ![]() radians followed by a rotation of
radians followed by a rotation of ![]() radians.[12] We see that
radians.[12] We see that ![]() is the reference angle for
is the reference angle for ![]() .
.
By The Reference Angle Theorem, ![]() and
and ![]() . As the terminal side of
. As the terminal side of ![]() falls in Quadrant III, both
falls in Quadrant III, both ![]() and
and ![]() are negative, so
are negative, so
![]() and
and ![]()

Example 7.2.3.2b
Suppose ![]() is an acute angle with
is an acute angle with ![]() .
.
State the sine and cosine of the following angles:
![]()
Solution:
State the sine and cosine of ![]() .
.
Rewriting ![]() as
as ![]() , we can plot
, we can plot ![]() by visualizing one complete revolution counter-clockwise followed by a clockwise revolution, or `backing up,’ of
by visualizing one complete revolution counter-clockwise followed by a clockwise revolution, or `backing up,’ of ![]() radians. Once again, we see that
radians. Once again, we see that ![]() is
is ![]() ‘s reference angle.
‘s reference angle.
Because ![]() is a Quadrant IV angle, we choose the appropriate signs and get:
is a Quadrant IV angle, we choose the appropriate signs and get:
![]() and
and ![]() .
.

Example 7.2.3.2c
Suppose ![]() is an acute angle with
is an acute angle with ![]() .
.
State the sine and cosine of the following angles:
![]()
Solution:
State the sine and cosine of ![]() .
.
Taking a cue from the previous problem, we rewrite ![]() as
as ![]() . The angle
. The angle ![]() represents one and a half revolutions counter-clockwise, so that when we `back up’
represents one and a half revolutions counter-clockwise, so that when we `back up’ ![]() radians, we end up in Quadrant II.
radians, we end up in Quadrant II.
As ![]() is the reference angle for
is the reference angle for ![]() , The Reference Angle Theorem gives
, The Reference Angle Theorem gives
![]() and
and ![]() .
.

Example 7.2.3.2d
Suppose ![]() is an acute angle with
is an acute angle with ![]() .
.
State the sine and cosine of the following angles:
![]()
Solution:
State the sine and cosine of ![]() .
.
To plot ![]() , we first rotate
, we first rotate ![]() radians and follow up with
radians and follow up with ![]() radians. The reference angle here is not
radians. The reference angle here is not ![]() , so The Reference Angle Theorem is not immediately applicable. (It’s important that you see why this is the case. Take a moment to think about this before reading on.)
, so The Reference Angle Theorem is not immediately applicable. (It’s important that you see why this is the case. Take a moment to think about this before reading on.)
Let ![]() be the point on the terminal side of
be the point on the terminal side of ![]() which lies on the Unit Circle so that
which lies on the Unit Circle so that ![]() and
and ![]() . Once we graph
. Once we graph ![]() in standard position, we use the fact from Geometry that equal angles subtend equal chords to show that the dotted lines in the figure below are equal.
in standard position, we use the fact from Geometry that equal angles subtend equal chords to show that the dotted lines in the figure below are equal.
Hence, ![]() . Similarly, we find
. Similarly, we find ![]() .
.

A couple of remarks about Example 7.2.3 are in order. First, we note the right triangle we used to find ![]() is a scaled 5-12-13 triangle. Recognizing this Pythagorean Triple[13] may have simplified our workflow. Along the same lines, because, the Unit Circle, by definition, is described by the equation
is a scaled 5-12-13 triangle. Recognizing this Pythagorean Triple[13] may have simplified our workflow. Along the same lines, because, the Unit Circle, by definition, is described by the equation ![]() , we could substitute
, we could substitute ![]() in order to find
in order to find ![]() . We leave it to the reader to show we get the exact same answer regardless of the approach used.
. We leave it to the reader to show we get the exact same answer regardless of the approach used.
Our next example turns the tables and makes good use of the Unit Circle values given previously as well as Theorem 7.3 in a different way: instead of giving information about the angle and asking for sine or cosine values, we are given sine or cosine values and asked to produce the corresponding angles. In other words, we solve some rudimentary equations involving sine and cosine.[14]
Example 7.2.4
Example 7.2.4.1
Determine all angles that satisfy the following equations. Express your answers in radians.[15]
![]()
Solution:
Determine all angles that satisfy ![]() .
.
If ![]() , then we know the terminal side of
, then we know the terminal side of ![]() , when plotted in standard position, intersects the Unit Circle at
, when plotted in standard position, intersects the Unit Circle at ![]() . This means
. This means ![]() is a Quadrant I or IV angle.
is a Quadrant I or IV angle.
Because ![]() , we know from the values on the given Unit Circle that the reference angle is
, we know from the values on the given Unit Circle that the reference angle is ![]() .
.

One solution in Quadrant I is ![]() .
.
Per Theorem 7.3, all other Quadrant I solutions must be coterminal with ![]() . Recall from Section 7.1.2, two angles in radian measure are coterminal if and only if they differ by an integer multiple of
. Recall from Section 7.1.2, two angles in radian measure are coterminal if and only if they differ by an integer multiple of ![]() . Hence to describe all angles coterminal with a given angle, we add
. Hence to describe all angles coterminal with a given angle, we add ![]() for integers
for integers ![]() ,
, ![]() ,
, ![]() , \dots. Hence, we record our final answer as
, \dots. Hence, we record our final answer as ![]() for integers
for integers ![]() .
.
Proceeding similarly for the Quadrant IV case, we find the solution to ![]() here is
here is ![]() , so our answer in this Quadrant is
, so our answer in this Quadrant is ![]() for integers
for integers ![]() .
.
Example 7.2.4.2
Determine all angles that satisfy the following equations. Express your answers in radians.
![]()
Solution:
Determine all angles that satisfy ![]() .
.
If ![]() , then when
, then when ![]() is plotted in standard position, its terminal side intersects the Unit Circle at
is plotted in standard position, its terminal side intersects the Unit Circle at ![]() . From this, we determine
. From this, we determine ![]() is a Quadrant III or Quadrant IV angle with reference angle
is a Quadrant III or Quadrant IV angle with reference angle ![]() .
.
In Quadrant III, one solution is ![]() , so we capture all Quadrant III solutions by adding integer multiples of
, so we capture all Quadrant III solutions by adding integer multiples of ![]() :
: ![]() .
.
In Quadrant IV, one solution is ![]() so all the solutions here are of the form
so all the solutions here are of the form ![]() for integers
for integers ![]() .
.
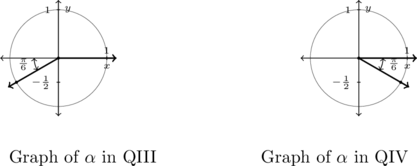
Example 7.2.4.3
Determine all angles that satisfy the following equations. Express your answers in radians.
![]()
Solution:
Determine all angles that satisfy ![]() .
.
If ![]() , then the terminal side of
, then the terminal side of ![]() must lie on the line
must lie on the line ![]() , also known as the
, also known as the ![]() -axis.
-axis.
![]()
While, technically speaking, ![]() isn’t a reference angle (it’s not acute), we can nonetheless use it to find our answers.
isn’t a reference angle (it’s not acute), we can nonetheless use it to find our answers.
If we follow the procedure set forth in the previous examples, we find ![]() and
and ![]() for integers,
for integers, ![]() .
.
While this solution is correct, it can be shortened to ![]() for integers
for integers ![]() . The reader is encouraged to see the geometry using the diagram above on the left.
. The reader is encouraged to see the geometry using the diagram above on the left.
Example 7.2.4.4
Determine all angles that satisfy the following equations. Express your answers in radians.
![]()
Solution:
Determine all angles that satisfy ![]() .
.
We are asked to solve ![]() . As sine values are
. As sine values are ![]() -coordinates on the Unit Circle,
-coordinates on the Unit Circle, ![]() can’t be any larger than
can’t be any larger than ![]() . Hence,
. Hence, ![]() has no solutions.
has no solutions.
One of the key items to take from Example 7.2.4 is that, in general, solutions to trigonometric equations consist of infinitely many answers. This is especially important when checking answers to the exercises.
For example, another Quadrant IV solution to ![]() is
is ![]() . Hence, the family of Quadrant IV answers to number 2 in the last example could just have easily been written
. Hence, the family of Quadrant IV answers to number 2 in the last example could just have easily been written ![]() for integers
for integers ![]() . While on the surface, this family may look different than the stated solution of
. While on the surface, this family may look different than the stated solution of ![]() for integers
for integers ![]() , we leave it to the reader to show they represent the same list of angles.
, we leave it to the reader to show they represent the same list of angles.
It is also worth noting that when asked to solve equations in algebra, we are usually looking for real number solutions. Thanks to the work we did previously on the identifications, we are able to regard the inputs to the sine and cosine functions as real numbers by identifying any real number ![]() with an oriented angle
with an oriented angle ![]() measuring
measuring ![]() radians. That is, for each real number
radians. That is, for each real number ![]() , we associate an oriented arc
, we associate an oriented arc ![]() units in length with initial point
units in length with initial point ![]() and endpoint
and endpoint ![]() .
.
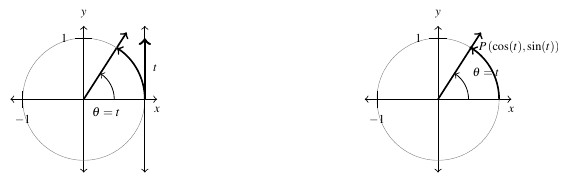
In practice this means in expressions like `![]() ‘ and `
‘ and `![]() ,’ the inputs can be thought of as either angles in radian measure or real numbers, whichever is more convenient.
,’ the inputs can be thought of as either angles in radian measure or real numbers, whichever is more convenient.
Suppose, as in the Exercises, we are asked to find all real number solutions to the equation such as ![]() . The discussion above allows us to find the real number solutions to this equation by thinking in angles. Indeed, we would solve this equation in the exact way we solved
. The discussion above allows us to find the real number solutions to this equation by thinking in angles. Indeed, we would solve this equation in the exact way we solved ![]() in Example 7.2.4 number 2. Our solution is only cosmetically different in that the variable used is
in Example 7.2.4 number 2. Our solution is only cosmetically different in that the variable used is ![]() rather than
rather than ![]() :
: ![]() or
or ![]() for integers,
for integers, ![]() .
.
We will study the sine and cosine functions in greater detail in Section 7.3. Until then, keep in mind that any properties of the sine and cosine functions developed in the following sections which regard them as functions of angles in radian measure apply equally well if the inputs are regarded as real numbers.
7.2.3 Beyond the Unit Circle
In Definition 7.3, we define the sine and cosine functions using the Unit Circle, ![]() . It turns out that we can use any circle centered at the origin to determine the sine and cosine values of angles. To show this, we essentially recycle the same similarity arguments used in Section 7.2.1 to show the trigonometric ratios described in Definition 7.2 are independent of the choice of right triangle used.[16]
. It turns out that we can use any circle centered at the origin to determine the sine and cosine values of angles. To show this, we essentially recycle the same similarity arguments used in Section 7.2.1 to show the trigonometric ratios described in Definition 7.2 are independent of the choice of right triangle used.[16]
Consider for the moment the acute angle ![]() drawn below in standard position. Let
drawn below in standard position. Let ![]() be the point on the terminal side of
be the point on the terminal side of ![]() which lies on the circle
which lies on the circle ![]() , and let
, and let ![]() be the point on the terminal side of
be the point on the terminal side of ![]() which lies on the Unit Circle. Now consider dropping perpendiculars from
which lies on the Unit Circle. Now consider dropping perpendiculars from ![]() and
and ![]() to create two right triangles,
to create two right triangles, ![]() and
and ![]() . These triangles are similar,[17] thus it follows that
. These triangles are similar,[17] thus it follows that ![]() , so
, so ![]() and, similarly, we find
and, similarly, we find ![]() . Because, by definition,
. Because, by definition, ![]() and
and ![]() , we get the coordinates of
, we get the coordinates of ![]() to be
to be ![]() and
and ![]() . By reflecting these points through the
. By reflecting these points through the ![]() -axis,
-axis, ![]() -axis and origin, we obtain the result for all non-quadrantal angles
-axis and origin, we obtain the result for all non-quadrantal angles ![]() , and we leave it to the reader to verify these formulas hold for the quadrantal angles as well.
, and we leave it to the reader to verify these formulas hold for the quadrantal angles as well.
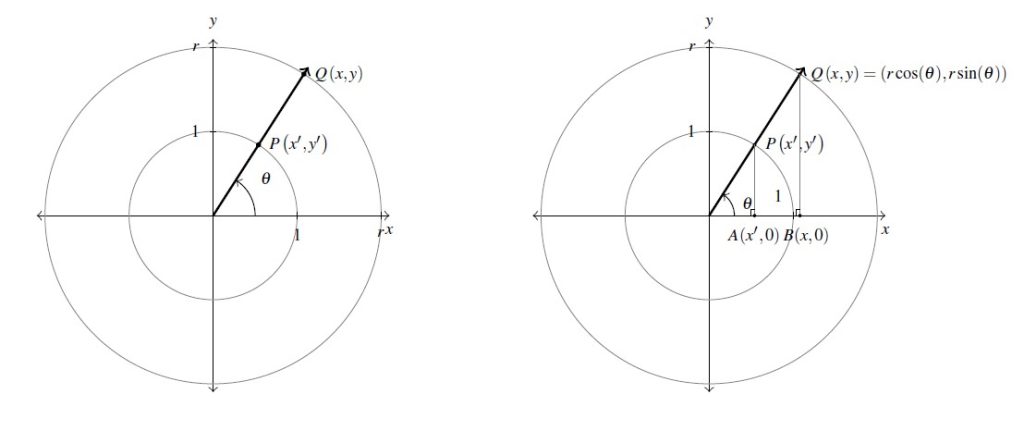
Not only can we describe the coordinates of ![]() in terms of
in terms of ![]() and
and ![]() but due to the fact that the radius of the circle is
but due to the fact that the radius of the circle is ![]() , we can also express
, we can also express ![]() and
and ![]() in terms of the coordinates of
in terms of the coordinates of ![]() . These results are summarized in the following theorem.
. These results are summarized in the following theorem.
Theorem 7.4
If ![]() is the point on the terminal side of an angle
is the point on the terminal side of an angle ![]() , plotted in standard position, which lies on the circle
, plotted in standard position, which lies on the circle ![]() then
then ![]() and
and ![]() . Moreover,
. Moreover,
![]()
Note that in the case of the Unit Circle we have ![]() , so Theorem 7.4 reduces to our definitions of
, so Theorem 7.4 reduces to our definitions of ![]() and
and ![]() in Definition 7.3. Our next example makes good use of Theorem 7.4.
in Definition 7.3. Our next example makes good use of Theorem 7.4.
Example 7.2.5
Example 7.2.5.1
Suppose that the terminal side of an angle ![]() , when plotted in standard position, contains the point
, when plotted in standard position, contains the point ![]() . Compute
. Compute ![]() and
and ![]() .
.
Solution:
Suppose that the terminal side of an angle ![]() , when plotted in standard position, contains the point
, when plotted in standard position, contains the point ![]() . Compute
. Compute ![]() and
and ![]() .
.
We are given both the ![]() and
and ![]() coordinates of a point on the terminal side of this angle, so we can use Theorem7.4 directly. First, we find
coordinates of a point on the terminal side of this angle, so we can use Theorem7.4 directly. First, we find
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} r &=& \sqrt{x^2+y^2} \\ &=& \sqrt{(-2)^2+4^2} \\ &=& \sqrt{20} \\ &=& 2\sqrt{5} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-40981cb69579cde80bff2d69d9c6bb1e_l3.png)
This means the point ![]() lies on a circle of radius
lies on a circle of radius ![]() units.
units.
Hence, ![]() and
and ![]() .
.

Example 7.2.5.2
Suppose ![]() with
with ![]() . Compute
. Compute ![]() .
.
Solution:
Suppose ![]() with
with ![]() . Compute
. Compute ![]() .
.
We are told ![]() , so, in particular,
, so, in particular, ![]() is a Quadrant II angle.
is a Quadrant II angle.
Per Theorem 7.4, ![]() where
where ![]() is the
is the ![]() -coordinate of the intersection point of the circle
-coordinate of the intersection point of the circle ![]() and the terminal side of
and the terminal side of ![]() (when plotted in standard position, of course!) For convenience, we choose
(when plotted in standard position, of course!) For convenience, we choose ![]() so that
so that ![]() , and we get the diagram.
, and we get the diagram.
Given ![]() , we get
, we get ![]() . We find
. We find ![]() , and because
, and because ![]() is a Quadrant II angle, we get
is a Quadrant II angle, we get ![]() .
.
Hence, ![]() .
.

Example 7.2.5.3
In Example 7.1.5 in Section 7.1.2, we approximated the radius of the earth at ![]() north latitude to be
north latitude to be ![]() miles. Justify this approximation if the spherical radius of the Earth is
miles. Justify this approximation if the spherical radius of the Earth is ![]() miles.
miles.
Solution:
In Example 7.1.5 in Section 7.1.2, we approximated the radius of the earth at ![]() north latitude to be
north latitude to be ![]() miles. Justify this approximation if the spherical radius of the Earth is
miles. Justify this approximation if the spherical radius of the Earth is ![]() miles.
miles.
Recall the diagram below on the left indicating the circles which are the parallels of latitude.[18]
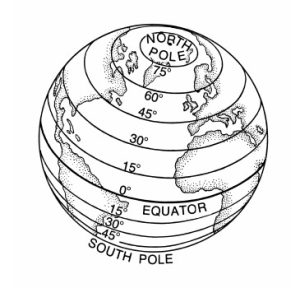

Assuming the Earth is a sphere of radius ![]() miles, a cross-section through the poles produces a circle of radius
miles, a cross-section through the poles produces a circle of radius ![]() miles. Viewing the Equator as the
miles. Viewing the Equator as the ![]() -axis, the value we seek is the
-axis, the value we seek is the ![]() -coordinate of the point
-coordinate of the point ![]() indicated in the figure above on the right. Using Theorem 7.4, we get
indicated in the figure above on the right. Using Theorem 7.4, we get ![]() . Hence, the radius of the Earth at North Latitude
. Hence, the radius of the Earth at North Latitude ![]() is approximately
is approximately ![]() miles.
miles.
Theorem 7.4 gives us what we need to `circle back’ to the question posed at the the beginning of the section: how to describe the position of an object traveling in a circular path of radius ![]() with constant angular velocity
with constant angular velocity ![]() . Suppose that at time
. Suppose that at time ![]() , the object has swept out an angle measuring
, the object has swept out an angle measuring ![]() radians. If we assume that the object is at the point
radians. If we assume that the object is at the point ![]() when
when ![]() , the angle
, the angle ![]() is in standard position. By definition,
is in standard position. By definition, ![]() which we rewrite as
which we rewrite as ![]() . According to Theorem 7.4, the location of the object
. According to Theorem 7.4, the location of the object ![]() on the circle is found using the equations
on the circle is found using the equations ![]() and
and ![]() . Hence, at time
. Hence, at time ![]() , the object is at the point
, the object is at the point ![]() , as seen in the diagram below.
, as seen in the diagram below.
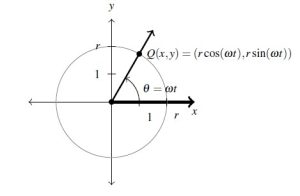
We have just argued the following.
Equation 7.3
Suppose an object is traveling in a circular path of radius ![]() centered at the origin with constant angular velocity
centered at the origin with constant angular velocity ![]() . If
. If ![]() corresponds to the point
corresponds to the point ![]() , then the
, then the ![]() and
and ![]() coordinates of the object are functions of
coordinates of the object are functions of ![]() and are given by
and are given by ![]() and
and ![]() . Here,
. Here, ![]() indicates a counter-clockwise direction and
indicates a counter-clockwise direction and ![]() indicates a clockwise direction.
indicates a clockwise direction.
Example 7.2.6
Example 7.2.6
Suppose we are in the situation of Example 7.1.5. Determine the equations of motion of Lakeland Community College as the earth rotates.
Solution:
From Example 7.1.5, we take ![]() miles and and
miles and and ![]() .
.
Hence, the equations of motion are
![]()
where ![]() and
and ![]() are measured in miles and
are measured in miles and ![]() is measured in hours.
is measured in hours.
7.2.4 Section Exercises
In Exercises 1 – 4, compute the requested quantities.
- Determine
 ,
,  , and
, and  .
.
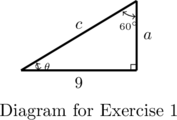
- Determine
 ,
,  , and
, and  .
.
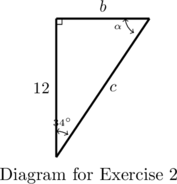
- Find
 ,
,  , and
, and  .
.
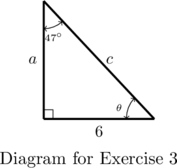
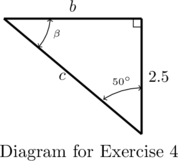
- Find
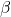 ,
,  , and
, and  .
.
In Exercises 5 – 7, answer the following questions assuming ![]() is an angle in a right triangle.
is an angle in a right triangle.
- If
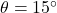 and the hypotenuse has length
and the hypotenuse has length 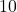 , how long is the side opposite
, how long is the side opposite  ?
? - If
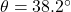 and the side opposite
and the side opposite  has length
has length 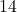 , how long is the hypotenuse?
, how long is the hypotenuse? - If
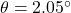 and the hypotenuse has length
and the hypotenuse has length 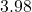 , how long is the side adjacent to
, how long is the side adjacent to  ?
?
In Exercises 8 – 27, determine the exact value of the cosine and sine of the given angle.
In Exercises 28 – 36, compute all of the angles which satisfy the given equation.
In Exercises 37 – 45, solve the equation for ![]() . (See the remarks in 7.2.2.)
. (See the remarks in 7.2.2.)
In Exercises 46 – 49, let ![]() be the angle in standard position whose terminal side contains the given point then compute
be the angle in standard position whose terminal side contains the given point then compute ![]() and
and ![]() .
.
In Exercises 50 – 59, use the results developed throughout the section to find the requested value.
- If
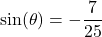 with
with  in Quadrant IV, what is
in Quadrant IV, what is 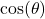 ?
? - If
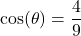 with
with  in Quadrant I, what is
in Quadrant I, what is 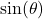 ?
? - If
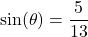 with
with  in Quadrant II, what is
in Quadrant II, what is 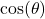 ?
? - If
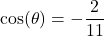 with
with  in Quadrant III, what is
in Quadrant III, what is 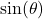 ?
? - If
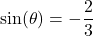 with
with  in Quadrant III, what is
in Quadrant III, what is 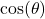 ?
? - If
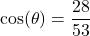 with
with  in Quadrant IV, what is
in Quadrant IV, what is 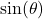 ?
? - If
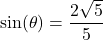 and
and 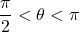 , what is
, what is 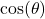 ?
? - If
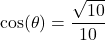 and
and 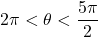 , what is
, what is 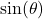 ?
? - If
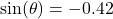 and
and 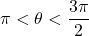 , what is
, what is 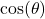 ?
? - If
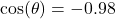 and
and 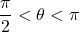 , what is
, what is 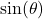 ?
?
In Exercises 60 – 64, write the given function as a nontrivial decomposition of functions as directed.
- For
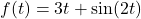 , find functions
, find functions  and
and  so that
so that 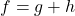 .
. - For
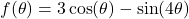 , find functions
, find functions  and
and  so that
so that 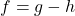 .
. - For
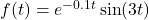 , find functions
, find functions  and
and  so that
so that 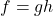 .
. - For
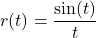 , find functions
, find functions  and
and  so
so 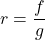 .
. - For
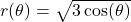 , find functions
, find functions  and
and  so
so 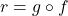 .
. - For each function
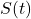 listed below, compute the average rate of change over the indicated interval.[19] What trends do you notice? Be sure your calculator is in radian mode!
listed below, compute the average rate of change over the indicated interval.[19] What trends do you notice? Be sure your calculator is in radian mode! ![Rendered by QuickLaTeX.com \[ \begin{array}{|r||c|c|c|} \hline S(t) & [-0.1, 0.1] & [-0.01, 0.01] &[-0.001, 0.001] \\ \hline \sin(t) &&& \\ \hline \sin(2t) &&& \\ \hline \sin(3t) &&& \\ \hline \sin(4t) &&& \\ \hline \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-6af8bf555014f6516d8f6b6298e3e13a_l3.png)
In Exercises 66 – 69, find the equations of motion for the given scenario. Assume that the center of the motion is the origin, the motion is counter-clockwise and that ![]() corresponds to a position along the positive
corresponds to a position along the positive ![]() -axis. (See Equation 7.3 and Example 7.1.5.)
-axis. (See Equation 7.3 and Example 7.1.5.)
- A point on the edge of the spinning yo-yo in Exercise 50 from Section 7.1.2.Recall: The diameter of the yo-yo is 2.25 inches and it spins at 4500 revolutions per minute.
- The yo-yo in exercise 52 from Section 7.1.2.Recall: The radius of the circle is 28 inches and it completes one revolution in 3 seconds.
- A point on the edge of the hard drive in Exercise 53 from Section 7.1.2.Recall: The diameter of the hard disk is 2.5 inches and it spins at 7200 revolutions per minute.
- A passenger on the Big Wheel in Exercise 55 from Section 7.1.2.Recall: The diameter is 128 feet and completes 2 revolutions in 2 minutes, 7 seconds.
- Consider the numbers: 0, 1, 2, 3, 4. Take the square root of each of these numbers, then divide each by 2. The resulting numbers should look hauntingly familiar.
- In this section, we saw that the sine and cosine functions of angles can be considered functions of real numbers. With help from your classmates, discuss the domains and ranges of
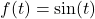 and
and 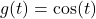 . Write your answers using interval notation.
. Write your answers using interval notation. - Another way to establish Theorem 7.4 is to use transformations. Transform the Unit Circle,
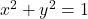 , to
, to 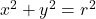 using horizontal and vertical stretches. Show if the coordinates on the Unit Circle are
using horizontal and vertical stretches. Show if the coordinates on the Unit Circle are 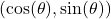 , then the corresponding coordinates on
, then the corresponding coordinates on 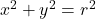 are
are 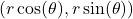 .
. - In the scenario of Equation 7.3, we assumed that at
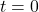 , the object was at the point
, the object was at the point 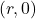 . If this is not the case, we can adjust the equations of motion by introducing a `time delay.’ If
. If this is not the case, we can adjust the equations of motion by introducing a `time delay.’ If 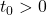 is the first time the object passes through the point
is the first time the object passes through the point 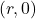 , show, with the help of your classmates, the equations of motion are
, show, with the help of your classmates, the equations of motion are 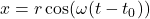 and
and 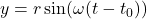 .
.
Section 7.2 Exercise Answers can be found in the Appendix … Coming soon
- Including one by Mentor, Ohio native President James Garfield. ↵
- We will prove this in Section 8.5 by generalizing the Pythagorean Theorem to a formula that works for all triangles. ↵
- That is, a triangle with the same `shape' - that is, the same angles. ↵
- We will do a little of this in Section 8.2. ↵
- See Definition 1.3 in Section 1.2. ↵
- See Section 1.1. ↵
- The etymology of the name `sine' is quite colorful, and the interested reader is invited to research it; the `co' in `cosine' is related to the concept of `co'mplementary angles (see Sections 7.1 and 7.2.1) and is explained in detail in Section 8.2. ↵
- For instance, Definition 7.2 in Section 7.2.1. ↵
- Do you see why? ↵
- Recall we say they are `coterminal.' ↵
- For once, we have something convenient about using radian measure in contrast to the abstract theoretical nonsense about using them as a `natural' way to match oriented angles with real numbers! ↵
- Because
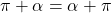 ,
,  may be plotted by reversing the order of rotations given here. You should do this. ↵
may be plotted by reversing the order of rotations given here. You should do this. ↵ - See Section 7.2.1 for more examples of Pythagorean Triples. ↵
- We will study equations in more detail in Section 8.3.2. ↵
- This ensures we keep building the `fluency with radians' which is so necessary for later work. ↵
- Another approach uses transformations. See Exercise 72. ↵
- Do you remember why? ↵
- Diagram credit: Pearson Scott Foresman [Public domain], via Wikimedia Commons. ↵
- See Definition 1.11 in Section 1.3.4 for a review of this concept, as needed. ↵

