0.2 Simplifying Radicals
Theorem 0.2 Simplifying 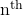 powers of
powers of 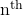 roots and
roots and 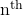 roots of
roots of 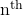 powers
powers
![Rendered by QuickLaTeX.com (\sqrt[n]{a})^{n} = a](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-76595362ba9eec59ad18ba85fe10ef46_l3.png)
- if
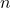 is odd,
is odd, ![Rendered by QuickLaTeX.com \sqrt[n]{a^{n}} = a](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-295166e888e5eff266d953c99428585f_l3.png) ; if
; if 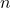 is even,
is even, ![Rendered by QuickLaTeX.com \sqrt[n]{a^{n}} = |a|](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-57e2df3d9bf3864512d05d6e0d79ce9a_l3.png) .
.
Because ![]() is defined so that
is defined so that ![]() , the first claim in the theorem is just a re-wording of Definition 0.2. The second part of the theorem breaks down along odd/even exponent lines due to how exponents affect negatives. To see this, consider the specific cases of
, the first claim in the theorem is just a re-wording of Definition 0.2. The second part of the theorem breaks down along odd/even exponent lines due to how exponents affect negatives. To see this, consider the specific cases of ![]() and
and ![]() .
.
In the first case, ![]() , so we have an instance of when
, so we have an instance of when ![]() . The reason that the cube root `undoes’ the third power in
. The reason that the cube root `undoes’ the third power in ![]() is because the negative is preserved when raised to the third (odd) power. In
is because the negative is preserved when raised to the third (odd) power. In ![]() , the negative `goes away’ when raised to the fourth (even) power:
, the negative `goes away’ when raised to the fourth (even) power:![]() . According to Definition 0.2, the fourth root is defined to give only non-negative numbers, so
. According to Definition 0.2, the fourth root is defined to give only non-negative numbers, so ![]() . Here we have a case where
. Here we have a case where ![]() , not
, not ![]() .
.
In general, we need the absolute values to simplify ![]() only when
only when ![]() is even because a negative to an even power is always positive. In particular,
is even because a negative to an even power is always positive. In particular, ![]() , not just `
, not just `![]() ‘ (unless we know
‘ (unless we know ![]() .)[2] We practice these formulas in the following example.
.)[2] We practice these formulas in the following example.
Example 0.2.1
Example 0.2.1.1
Perform the indicated operations and simplify.
![]()
Solution:
Simplify ![]() .
.
We told you previously that roots do not `distribute’ across addition and due to the fact that ![]() does not factor over the real numbers,
does not factor over the real numbers, ![]() cannot be simplified.
cannot be simplified.
It may seem silly to start with this example but it is extremely important that you understand what maneuvers are legal and which ones are not.[3]
Example 0.2.1.2
Perform the indicated operations and simplify.
![]()
Example 0.2.1.3
Perform the indicated operations and simplify.
![]()
Solution:
Simplify ![]() .
.
To simplify ![]() , we need to look for perfect cubes in the radicand. For the cofficient, we have
, we need to look for perfect cubes in the radicand. For the cofficient, we have ![]() .
.
To find the largest perfect cube factor in ![]() , we divide
, we divide ![]() (the exponent on
(the exponent on ![]() ) by
) by ![]() (because we are looking for a perfect cube). We get
(because we are looking for a perfect cube). We get ![]() with a remainder of
with a remainder of ![]() .
.
This means ![]() , so
, so
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} x^{14} &=& x^{4 \cdot 3 + 2} \\ &=& x^{4 \cdot 3} x^2 \\ &=& (x^4)^3 x^2 .\end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-435bc1800744c4a19071bf24f1f74694_l3.png)
Putting this altogether gives:
![Rendered by QuickLaTeX.com \[\begin{array}{rclr} \sqrt[3]{48x^{14}} & = & \sqrt[3]{2^3 \cdot 6 \cdot(x^4)^3 x^2} & \text{Factor out perfect cubes} \\ [2pt] & = & \sqrt[3]{2^3} \sqrt[3]{(x^4)^3} \sqrt[3]{6x^2} & \text{Rearrange factors, Product Rule of Radicals} \\ [2pt] & = & 2x^4\sqrt[3]{6x^2} & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-96ba164d3ecf87d9a5941d399ff4c44a_l3.png)
Example 0.2.1.4
Perform the indicated operations and simplify.
![]()
Solution:
Simplify ![]() .
.
In this example, we are looking for perfect fourth powers in the radicand. In the numerator, ![]() , is clearly a perfect fourth power. For the denominator, we take the power on the
, is clearly a perfect fourth power. For the denominator, we take the power on the ![]() , namely
, namely ![]() , and divide by
, and divide by ![]() to get
to get ![]() . This means
. This means ![]() . We get
. We get
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \sqrt[4]{\dfrac{\pi r^{4}}{L^{8}}} & = & \dfrac{\sqrt[4]{\pi r^{4}}}{\sqrt[4]{L^{8}}} & \text{Quotient Rule of Radicals} \\ [12pt] & = & \dfrac{\sqrt[4]{\pi}\sqrt[4]{r^{4}}}{\sqrt[4]{(L^2)^{4}}} & \text{Product Rule of Radicals} \\ [12pt] & = & \dfrac{\sqrt[4]{\pi}|r|}{|L^2|} & \text{Simplify} \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-faeec99614a81536a5f74a3346cf09e5_l3.png)
![]()
Example 0.2.1.5
Perform the indicated operations and simplify.
![]()
Solution:
Simplify ![]() .
.
After a quick division (two of the ![]() ‘s in the second term) we need to obtain a common denominator. We can view the first term as having a denominator of
‘s in the second term) we need to obtain a common denominator. We can view the first term as having a denominator of ![]() , thus the common denominator is precisely the denominator of the second term, namely
, thus the common denominator is precisely the denominator of the second term, namely ![]() . With common denominators, we proceed to add the two fractions. Our last step is to factor the numerator to see if there are any opportunities to divide out common factors in the numerator and denominator.
. With common denominators, we proceed to add the two fractions. Our last step is to factor the numerator to see if there are any opportunities to divide out common factors in the numerator and denominator.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 2x \sqrt[3]{x^2-4} + 2\left(\dfrac{1}{2(\sqrt[3]{x^2-4})^2}\right) (2x) & = & 2x \sqrt[3]{x^2-4} + \cancel{2}\left(\dfrac{1}{\cancel{2}(\sqrt[3]{x^2-4})^2}\right) (2x) & \text{Reduce}\\ [12pt] & = & 2x \sqrt[3]{x^2-4} + \dfrac{2x}{(\sqrt[3]{x^2-4})^2} & \text{Mutiply} \\[12pt] & = & (2x \sqrt[3]{x^2-4}) \cdot \dfrac{(\sqrt[3]{x^2-4})^2}{(\sqrt[3]{x^2-4})^2} + \dfrac{2x}{(\sqrt[3]{x^2-4})^2} & \hspace*{-.1in}\text{\small Equivalent} \\ [-8pt] & & & \text{\small fractions} \\ & = & \dfrac{2x(\sqrt[3]{x^2-4})^3}{(\sqrt[3]{x^2-4})^2} + \dfrac{2x}{(\sqrt[3]{x^2-4})^2} & \text{Multiply}\\[12pt] & = & \dfrac{2x(x^2-4)}{(\sqrt[3]{x^2-4})^2} + \dfrac{2x}{(\sqrt[3]{x^2-4})^2} & \text{Simplify}\\ [12pt] & = & \dfrac{2x(x^2-4) + 2x}{(\sqrt[3]{x^2-4})^2} & \text{Add} \\ [12pt] & = & \dfrac{2x(x^2-4 +1)}{(\sqrt[3]{x^2-4})^2} & \text{Factor}\\ [12pt] & = & \dfrac{2x(x^2-3)}{(\sqrt[3]{x^2-4})^2} & \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a899d9a38a1e6e84030bfd93269a3892_l3.png)
We cannot reduce this any further, because ![]() is irreducible over the rational numbers.
is irreducible over the rational numbers.
Example 0.2.1.6
Perform the indicated operations and simplify.
![]()
Solution:
Simplify ![]() .
.
We begin by working inside each set of parentheses, using the product rule for radicals and combining like terms.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \sqrt{(\sqrt{18y} - \sqrt{8y})^2 + (\sqrt{20} - \sqrt{80})^2} & = & \sqrt{(\sqrt{9\cdot 2y} - \sqrt{4 \cdot 2y})^2 + (\sqrt{4\cdot 5} - \sqrt{16 \cdot 5})^2} & \\[8pt] & = & \sqrt{(\sqrt{9} \sqrt{2y} - \sqrt{4}\sqrt{2y})^2 + (\sqrt{4}\sqrt{5} - \sqrt{16}\sqrt{5})^2} & \\[8pt] & = & \sqrt{(3\sqrt{2y} - 2\sqrt{2y})^2 + (2\sqrt{5} - 4\sqrt{5})^2} & \\[8pt] & = & \sqrt{(\sqrt{2y})^2 + (-2\sqrt{5})^2} & \\[8pt] & = & \sqrt{2y + (-2)^2(\sqrt{5})^2} & \\[8pt] & = & \sqrt{2y + 4\cdot 5} & \\[8pt] & = & \sqrt{2y + 20} & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7501c07df10fe52cde9aa7f0ea9d5b73_l3.png)
To see if this simplifies any further, we factor the radicand: ![]() . Finding no perfect square factors, we are done.
. Finding no perfect square factors, we are done.
0.2.1 Section Exercises
In Exercises 1 – 13, perform the indicated operations and simplify.
Section 0.2 Exercise Answers can be found in the Appendix … Coming soon
- See Sections 4.1.2 and 5.1 for a more precise understanding of what we mean here. ↵
- This discussion should sound familiar - see the discussion following Definition 0.3 and the discussion following `Extracting the Square Root'. ↵
- You really do need to understand this otherwise horrible evil will plague your future studies in Math. If you say something totally wrong like
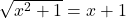 then you may never pass Calculus. PLEASE be careful! ↵
then you may never pass Calculus. PLEASE be careful! ↵ - Let
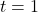 and see what happens to
and see what happens to 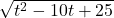 versus
versus 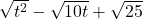 . ↵
. ↵ - In general,
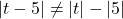 and
and 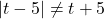 so watch what you're doing! ↵
so watch what you're doing! ↵

![Rendered by QuickLaTeX.com \sqrt[4]{\dfrac{32 \pi \varepsilon^8}{\rho^{12}}}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-624dc1dc790c75e391e9fa19b7fb6468_l3.png)
![Rendered by QuickLaTeX.com 2 \sqrt[3]{1-z} + 2z \left(\dfrac{1}{3 \left(\sqrt[3]{1-z}\right)^2}\right)(-1)](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e5f05158d2560b72a348cdeefd32d086_l3.png)
![Rendered by QuickLaTeX.com \dfrac{3}{\sqrt[3]{2x-1}} + (3x)\left(-\dfrac{1}{3 \left(\sqrt[3]{2x-1} \right)^4}\right)(2)](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4cb39aa37aaf4e9f304ef0daf4a7878e_l3.png)
