8.1 Fundamental and Pythagorean Identities
In Section 7.4, we first encountered the concept of an identity when discussing Theorem 7.8. Recall that an identity is an equation which is true regardless of the choice of variable. Identities are important in mathematics because they facilitate changing forms.[1]
We take a moment to generalize Theorem 7.8 below.
Theorem 8.1 Reciprocal and Quotient Identities
The following relationships hold for all angles ![]() provided each side of each equation is defined.
provided each side of each equation is defined.
It is important to remember that the equivalences stated in Theorem 8.1 are valid only when all quantities described therein are defined. As an example, ![]() , but
, but ![]() because
because ![]() is undefined.
is undefined.
When it comes down to it, the Reciprocal and Quotient Identities amount to giving different ratios on the Unit Circle different names. The main focus of this section is on a more algebraic relationship between certain pairs of the circular functions: the Pythagorean Identities.
Recall in Definition 7.3, the cosine and sine of an angle is defined as the ![]() and
and ![]() -coordinate, respectively, of a point on the Unit Circle. The coordinates of all points
-coordinate, respectively, of a point on the Unit Circle. The coordinates of all points ![]() on the Unit Circle satisfy the equation
on the Unit Circle satisfy the equation ![]() , thus we get for all angles
, thus we get for all angles ![]() ,
, ![]() . An unfortunate[2] convention, which the authors are compelled to perpetuate, is to write
. An unfortunate[2] convention, which the authors are compelled to perpetuate, is to write ![]() as
as ![]() and
and ![]() as
as ![]() . Rewriting the identity using this convention results in the following theorem, which is without a doubt one of the most important results in Trigonometry.
. Rewriting the identity using this convention results in the following theorem, which is without a doubt one of the most important results in Trigonometry.
The moniker `Pythagorean’ brings to mind the Pythagorean Theorem, from which both the Distance Formula and the equation for a circle are ultimately derived.[3] The word `Identity’ reminds us that, regardless of the angle ![]() , the equation in Theorem 8.2 is always true.
, the equation in Theorem 8.2 is always true.
If one of ![]() or
or ![]() is known, Theorem 8.2 can be used to determine the other, up to a (
is known, Theorem 8.2 can be used to determine the other, up to a (![]() ) sign. If, in addition, we know where the terminal side of
) sign. If, in addition, we know where the terminal side of ![]() lies when in standard position, then we can remove the ambiguity of the (
lies when in standard position, then we can remove the ambiguity of the (![]() ) and completely determine the missing value.[4] We illustrate this approach in the following example.
) and completely determine the missing value.[4] We illustrate this approach in the following example.
Example 8.1.1
Example 8.1.1.1
Use Theorem 8.2 and the given information to compute the indicated value.
If ![]() is a Quadrant II angle with
is a Quadrant II angle with ![]() , compute
, compute ![]() .
.
Solution:
If ![]() is a Quadrant II angle with
is a Quadrant II angle with ![]() , compute
, compute ![]() .
.
When we substitute ![]() into The Pythagorean Identity,
into The Pythagorean Identity, ![]() , we obtain
, we obtain ![]() .
.
Solving, we find ![]() .
.
Given ![]() is a Quadrant II angle, we know
is a Quadrant II angle, we know ![]() .
.
Hence, we select ![]() .
.
Example 8.1.1.2
Use Theorem 8.2 and the given information to compute the indicated value.
If ![]() with
with ![]() , compute
, compute ![]() .
.
Solution:
If ![]() with
with ![]() , compute
, compute ![]() .
.
Here we’re using the variable ![]() instead
instead ![]() which usually corresponds to a real number variable instead of an angle. As usual, we associate real numbers
which usually corresponds to a real number variable instead of an angle. As usual, we associate real numbers ![]() with angles
with angles ![]() measuring
measuring ![]() radians,[5] so the Pythagorean Identity works equally well for all real numbers
radians,[5] so the Pythagorean Identity works equally well for all real numbers ![]() as it does for all angles
as it does for all angles ![]() .
.
Substituting ![]() into
into ![]() gives
gives ![]() .
.
Given ![]() , we know
, we know ![]() corresponds to a Quadrant III angle, so
corresponds to a Quadrant III angle, so ![]() .
.
Hence, ![]() .
.
Example 8.1.1.3
Use Theorem 8.2 and the given information to compute the indicated value.
If ![]() , compute
, compute ![]() .
.
Solution:
If ![]() , compute
, compute ![]() .
.
When we substitute ![]() into
into ![]() , we find
, we find ![]() .
.
The reader is encouraged to compare and contrast the solution strategies demonstrated in Example 8.1.1 with those showcases in Examples 7.2.3 and 7.2.5 in Section 7.2.2.
As with many tools in mathematics, identities give us a different way to approach and solve problems.[6] As always, the key is to determine which approach makes the most sense (is more efficient, for instance) in the given scenario.
Our next task is to use the Reciprocal and Quotient Identities found in Theorem 8.1 coupled with the Pythagorean Identity found in Theorem 8.2 to derive new Pythagorean-like identities for the remaining four circular functions.
Assuming ![]() , we may start with
, we may start with ![]() and divide both sides by
and divide both sides by ![]() to obtain
to obtain
![]()
Using properties of exponents along with the Reciprocal and Quotient Identities, this reduces to
![]()
If ![]() , we can divide both sides of the identity
, we can divide both sides of the identity ![]() by
by ![]() , apply Theorem 8.1 once again, and obtain
, apply Theorem 8.1 once again, and obtain
![]()
Theorem 8.3 The Pythagorean Identities
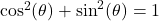
Common Alternate Forms:
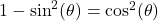
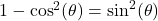
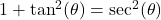 , provided
, provided 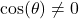
Common Alternate Forms:
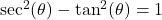
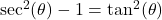
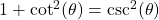 , provided
, provided 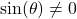 .
.
Common Alternate Forms:
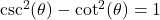
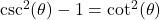
As usual, the formulas states in Theorem 8.3 work equally well for (the applicable) angles as well as real numbers.
Example 8.1.2
Example 8.1.2.1
Use Theorems 8.1 and 8.3 to determine the indicated values.
If ![]() is a Quadrant IV angle with
is a Quadrant IV angle with ![]() , determine
, determine ![]() .
.
Solution:
If ![]() is a Quadrant IV angle with
is a Quadrant IV angle with ![]() , determine
, determine ![]() .
.
Per Theorem 8.3, ![]() .
.
Given ![]() , we have
, we have ![]() , or
, or ![]() .
.
Because ![]() is a Quadrant IV angle, we know
is a Quadrant IV angle, we know ![]() so
so ![]() .
.
Example 8.1.2.2
Use Theorems 8.1 and 8.3 to determine the indicated values.
Compute ![]() if
if ![]() and
and ![]() .
.
Solution:
Compute ![]() if
if ![]() and
and ![]() .
.
Again, using Theorem 8.3, we have ![]() , so we have
, so we have ![]() .
.
This gives ![]() .
.
Given ![]() ,
, ![]() corresponds to a Quadrant III angle, so
corresponds to a Quadrant III angle, so ![]() .
.
Example 8.1.2.3
Use Theorems 8.1 and 8.3 to determine the indicated values.
If ![]() is a Quadrant II angle with
is a Quadrant II angle with ![]() , determine the exact values of the remaining circular functions.
, determine the exact values of the remaining circular functions.
Solution:
If ![]() is a Quadrant II angle with
is a Quadrant II angle with ![]() , determine the exact values of the remaining circular functions.
, determine the exact values of the remaining circular functions.
With five function values to find, we have our work cut out for us. From Theorem 8.1, we know ![]() , so we (quickly) get
, so we (quickly) get ![]() .
.
Next, we go after ![]() because between
because between ![]() and
and ![]() , we can get all of the remaining values courtesy of Theorem 8.1.
, we can get all of the remaining values courtesy of Theorem 8.1.
From Theorem 8.3, we have ![]() , so
, so
![]()
Hence, ![]() but
but ![]() is a Quadrant II angle, so we select
is a Quadrant II angle, so we select ![]() .
.
Back to Theorem 8.1, we get
![]() ,
,
![]() , and
, and
![]() .
.
Again, the reader is encouraged to study the solution methodology illustrated in Example 8.1.2 as compared with that employed in Example 7.4.3 in Section 7.4.
Trigonometric identities play an important role in not just Trigonometry, but in Calculus as well. We’ll use them in this book to find the values of the circular functions of an angle and solve equations and inequalities. In Calculus, they are needed to simplify otherwise complicated expressions. In the next example, we make good use of the Theorems 8.1 and 8.3.
Example 8.1.3
Example 8.1.3.1
Verify the following identities. Assume that all quantities are defined.
![]()
Solution:
In verifying identities, we typically start with the more complicated side of the equation and use known identities to transform it into the other side of the equation.
Verify ![]() .
.
Starting with the right hand side of ![]() , we use
, we use ![]() and find:
and find:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \sin(\theta) \sec(\theta) &=& \sin(\theta) \dfrac{1}{\cos(\theta)} \\[10pt] &=& \dfrac{\sin(\theta)}{\cos(\theta)} \\[10pt] &=& \tan(\theta), \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-bec4df4792f03ad1777550147fa4fecb_l3.png)
where the last equality is courtesy of Theorem 8.1.
Example 8.1.3.2
Verify the following identities. Assume that all quantities are defined.
![]()
Solution:
In verifying identities, we typically start with the more complicated side of the equation and use known identities to transform it into the other side of the equation.
Verify ![]() .
.
Expanding the left hand side, we get: ![]() . From Theorem 8.3, we know
. From Theorem 8.3, we know ![]() , which isn’t quite what we have. We are off by a negative sign (
, which isn’t quite what we have. We are off by a negative sign (![]() ), so we factor it out:
), so we factor it out:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} (\tan(t) - \sec(t)) (\tan(t) + \sec(t)) &=& \tan^{2}(t) - \sec^{2}(t) \\ &=& (-1)( \sec^{2}(t) - \tan^{2}(t)) \\ &=& (-1)(1) = -1. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-93ac7598fa748a1db21ef8f6a6129d6e_l3.png)
Example 8.1.3.3
Verify the following identities. Assume that all quantities are defined.
![]()
Solution:
In verifying identities, we typically start with the more complicated side of the equation and use known identities to transform it into the other side of the equation.
Verify ![]() .
.
Starting with the right hand side,[7] we notice we have a quantity we can immediately simplify per Theorem 8.3: ![]() . This increases the number of factors of cosine, (which is part of our goal in looking at the left hand side), so we proceed:
. This increases the number of factors of cosine, (which is part of our goal in looking at the left hand side), so we proceed:
![]()
Example 8.1.3.4
Verify the following identities. Assume that all quantities are defined.
![]()
Solution:
In verifying identities, we typically start with the more complicated side of the equation and use known identities to transform it into the other side of the equation.
Verify ![]() .
.
While both sides of our next identity contain fractions, the left side affords us more opportunities to use our identities.[8] Substituting ![]() and
and ![]() , we get:
, we get:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \dfrac{\sec(t)}{1 - \tan(t)} & = & \dfrac{ \dfrac{1}{\cos(t)}}{1 - \dfrac{\sin(t)}{\cos(t)}} \\[0.4in] &=& \dfrac{ \dfrac{1}{\cos(t)}}{1 - \dfrac{\sin(t)}{\cos(t)}} \cdot \dfrac{\cos(t)}{\cos(t)} \\[0.4in] & = & \dfrac{\left( \dfrac{1}{\cos(t)} \right) ( \cos(t) )}{\left(1 - \dfrac{\sin(t)}{\cos(t)}\right)(\cos(t))} \\[0.4in] &=& \dfrac{1}{(1)(\cos(t)) - \left(\dfrac{\sin(t)}{\cos(t)}\right)(\cos(t))} \\[0.4in] & = & \dfrac{1}{\cos(t) - \sin(t)}, \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-efeb6ef41fff7058a7a7a79d052a38bf_l3.png)
which is exactly what we had set out to show.
Example 8.1.3.5
Verify the following identities. Assume that all quantities are defined.
![]()
Solution:
In verifying identities, we typically start with the more complicated side of the equation and use known identities to transform it into the other side of the equation.
Verify ![]() .
.
Starting with the right hand side, we can get started by obtaining common denominators to add:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \dfrac{3}{1-\sin(x)} - \dfrac{3}{1 + \sin(x)} & = & \dfrac{3(1 + \sin(x))}{(1-\sin(x))(1 + \sin(x))} - \dfrac{3(1-\sin(x))}{(1 + \sin(x))(1-\sin(x))} \\ [.25in] & = & \dfrac{3 + 3\sin(x)}{1 - \sin^{2}(x)} - \dfrac{3 - 3\sin(x)}{1 - \sin^{2}(x)} \\ [.25in] & = & \dfrac{(3 + 3\sin(x)) - (3 - 3\sin(x))}{1 - \sin^{2}(x)} \\ [.25in] & = & \dfrac{6 \sin(x)}{1 - \sin^{2}(x)} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-8d80a262359c79280d1a75604dfcb273_l3.png)
At this point, we have at least reduced the number of fractions from two to one, it may not be clear how to proceed. When this happens, it isn’t a bad idea to start working with the other side of the identity to get some clues how to proceed.
Using a reciprocal and quotient identity, we find ![]() .
.
Theorem 8.3 tells us ![]() , which means to our surprise and delight, we are much closer to our goal that we may have originally thought:
, which means to our surprise and delight, we are much closer to our goal that we may have originally thought:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \dfrac{3}{1-\sin(x)} - \dfrac{3}{1 + \sin(x)} & = & \dfrac{6 \sin(x)}{1 - \sin^{2}(x)} \\[0.25in] &=& \dfrac{6 \sin(x)}{\cos^{2}(x)} \\ [.25in] & = & 6 \left(\dfrac{1}{\cos(x)}\right)\left( \dfrac{\sin(x)}{\cos(x)}\right) \\[0.25in] &=& 6 \sec(x) \tan(x). \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7c9e283aaac5c7a84934ddcba09fe9ad_l3.png)
Example 8.1.3.6
Verify the following identities. Assume that all quantities are defined.
![]()
Solution:
In verifying identities, we typically start with the more complicated side of the equation and use known identities to transform it into the other side of the equation.
Verify ![]() .
.
It is debatable which side of the identity is more complicated. One thing which stands out is that the denominator on the left hand side is ![]() , while the numerator of the right hand side is
, while the numerator of the right hand side is ![]() . This suggests the strategy of starting with the left hand side and multiplying the numerator and denominator by the quantity
. This suggests the strategy of starting with the left hand side and multiplying the numerator and denominator by the quantity ![]() . Theorem 8.3 comes to our aid once more when we simplify
. Theorem 8.3 comes to our aid once more when we simplify ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \dfrac{\sin(\theta)}{1 - \cos(\theta)} & = & \dfrac{\sin(\theta)}{(1 - \cos(\theta))} \cdot \dfrac{(1 + \cos(\theta))}{(1 + \cos(\theta))} \\[0.25in] &=& \dfrac{\sin(\theta)(1 + \cos(\theta))}{(1 - \cos(\theta))(1 + \cos(\theta))} \\ [.25in] & = & \dfrac{\sin(\theta)(1 + \cos(\theta))}{1 - \cos^{2}(\theta)} = \dfrac{\sin(\theta)(1 + \cos(\theta))}{\sin^{2}(\theta)} \\ [.25in] & = & \dfrac{\cancel{\sin(\theta)}(1 + \cos(\theta))}{\cancel{\sin(\theta)}\sin(\theta)} \\[0.25in] &=& \dfrac{1 + \cos(\theta)}{\sin(\theta)} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e0796c2effb8546f326feb41cf118829_l3.png)
In Example 8.1.3 number 6 above, we see that multiplying ![]() by
by ![]() produces a difference of squares that can be simplified to one term using Theorem 8.3.
produces a difference of squares that can be simplified to one term using Theorem 8.3.
This is exactly the same kind of phenomenon that occurs when we multiply expressions such as ![]() by
by ![]() or
or ![]() by
by ![]() . In algebra, these sorts of expressions were called `conjugates.’[9]
. In algebra, these sorts of expressions were called `conjugates.’[9]
For this reason, the quantities ![]() and
and ![]() are called `Pythagorean Conjugates.’ Below is a list of other common Pythagorean Conjugates.
are called `Pythagorean Conjugates.’ Below is a list of other common Pythagorean Conjugates.
Verifying trigonometric identities requires a healthy mix of tenacity and inspiration. You will need to spend many hours struggling with them just to become proficient in the basics.
Like many things in life, there is no short-cut here — there is no complete algorithm for verifying identities. Nevertheless, a summary of some strategies which may be helpful (depending on the situation) is provided below and ample practice is provided for you in the Exercises.
Strategies for Verifying Identities
- Try working on the more complicated side of the identity.
- Use the Reciprocal and Quotient Identities in Theorem 8.1 to write functions on one side of the identity in terms of the functions on the other side of the identity.
Simplify the resulting complex fractions. - Add rational expressions with unlike denominators by obtaining common denominators.
- Use the Pythagorean Identities in Theorem 8.3 to `exchange’ sines and cosines, secants and tangents, cosecants and cotangents, and simplify sums or differences of squares to one term.
- Multiply numerator and denominator by Pythagorean Conjugates in order to take advantage of the Pythagorean Identities in Theorem 8.3.
- If you find yourself stuck working with one side of the identity, try starting with the other side of the identity and see if you can find a way to bridge the two parts of your work.
- Try something. The more you work with identities, the better you’ll get with identities.
8.1.1 Section Exercises
In Exercises 1- 11, use the Reciprocal and Quotient Identities (Theorem 8.1) along with the Pythagorean Identities (Theorem 8.3), to compute the value of the circular function requested below. (Compute the exact value unless otherwise indicated.)
- If
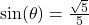 , compute
, compute 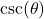 .
. - If
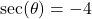 , compute
, compute 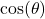 .
. - If
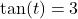 , compute
, compute 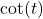 .
. - If
 is a Quadrant IV angle with
is a Quadrant IV angle with 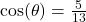 , compute
, compute 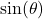 .
. - If
 is a Quadrant III angle with
is a Quadrant III angle with 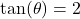 , compute
, compute 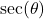 .
. - If
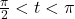 with
with 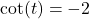 , compute
, compute 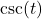 .
. - If
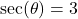 and
and 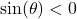 , compute
, compute 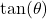 .
. - If
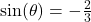 but
but 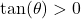 , compute
, compute 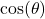 .
. - If
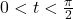 and
and 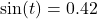 , compute
, compute 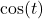 , rounded to four decimal places.
, rounded to four decimal places. - If
 is Quadrant IV angle with
is Quadrant IV angle with 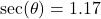 , compute
, compute 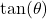 , rounded to four decimal places.
, rounded to four decimal places. - If
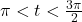 with
with 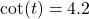 , compute
, compute 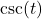 , rounded to four decimal places.
, rounded to four decimal places.
In Exercises 12 – 25, use the Reciprocal and Quotient Identities (Theorem 8.1) along with the Pythagorean Identities (Theorem 8.3), to compute the exact values of the remaining circular functions.
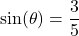 with
with  in Quadrant II
in Quadrant II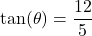 with
with  in Quadrant III
in Quadrant III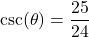 with
with  in Quadrant I
in Quadrant I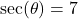 with
with  in Quadrant IV
in Quadrant IV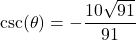 with
with  in Quadrant III
in Quadrant III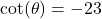 with
with  in Quadrant II
in Quadrant II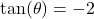 with
with  in Quadrant IV
in Quadrant IV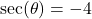 with
with  in Quadrant II
in Quadrant II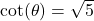 with
with  in Quadrant III
in Quadrant III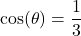 with
with  in Quadrant I
in Quadrant I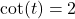 with
with 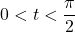
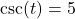 with
with 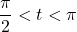
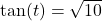 with
with 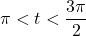
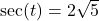 with
with 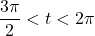
- Skippy claims
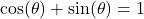 is an identity because when
is an identity because when 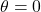 , the equation is true. Is Skippy correct? Explain.
, the equation is true. Is Skippy correct? Explain.
In Exercises 27 – 73, verify the identity. Assume that all quantities are defined.
In Exercises 74 – 77, verify the identity. You may need to consult Sections 1.4 and 5.4 for a review of the properties of absolute value and logarithms before proceeding.
Section 8.1 Exercise Answers can be found in the Appendix … Coming soon
- We've seen the utility of changing form throughout the text, most recently when we completed the square in Chapter 2 to put general quadratic equations into standard form in order to graph them. ↵
- This is unfortunate from a `function notation' perspective. See Section 7.6. ↵
- See Section 1.1 for details. ↵
- See the illustration following Example 7.4.2 to refresh yourself which circular functions are positive in which quadrants. ↵
- See Section 7.1 if you need a review of how we associate real numbers with angles in radian measure. ↵
- For example, factoring, completing the square, and the quadratic formula are three different (yet equivalent) ways to solve a quadratic equation. See Section 0.5.5 for a refresher. ↵
- We hope by this point a shift of variable to `
 ' instead of `
' instead of ` ' or `
' or ` ' is a non-issue. ↵
' is a non-issue. ↵ - Or, to put to another way, earn more partial credit if this were an exam question! ↵
- See Sections 0.5.6 and 0.2. ↵

