Appendix 1: Homework Answers for Chapter 1
Section 1.1 Answers
- The required points
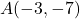 ,
, 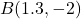 ,
, 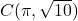 ,
, 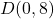 ,
, 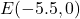 ,
, 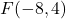 ,
, 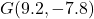 , and
, and 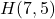 are plotted in the Cartesian Coordinate Plane below.
are plotted in the Cartesian Coordinate Plane below.
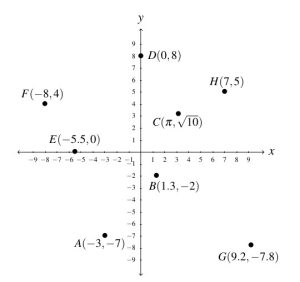
- Points
- The point
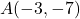 is
is
- in Quadrant III
- symmetric about the
 -axis with
-axis with 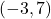
- symmetric about
 -axis with
-axis with 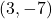
- symmetric about origin with
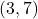
- The point
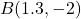 is
is
- in Quadrant IV
- symmetric about
 -axis with
-axis with 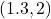
- symmetric about
 -axis with
-axis with 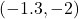
- symmetric about origin with
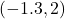
- The point
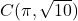 is
is
- in Quadrant I
- symmetric about
 -axis with
-axis with 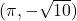
- symmetric about
 -axis with
-axis with 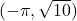
- symmetric about origin with
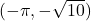
- The point
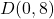 is
is
- on the positive
 -axis
-axis - symmetric about
 -axis with
-axis with 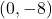
- symmetric about
 -axis with
-axis with 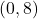
- symmetric about origin with
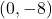
- on the positive
- The point
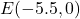 is
is
- on the negative
 -axis
-axis - symmetric about
 -axis with
-axis with 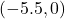
- symmetric about
 -axis with
-axis with 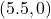
- symmetric about origin with
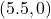
- on the negative
- The point
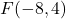 is
is
- in Quadrant II
- symmetric about
 -axis with
-axis with 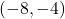
- symmetric about
 -axis with
-axis with 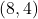
- symmetric about origin with
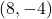
- The point
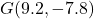 is
is
- in Quadrant IV
- symmetric about
 -axis with
-axis with 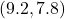
- symmetric about
 -axis with
-axis with 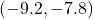
- symmetric about origin with
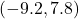
- The point
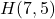 is
is
- in Quadrant I
- symmetric about
 -axis with
-axis with 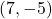
- symmetric about
 -axis with
-axis with 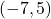
- symmetric about origin with
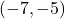
- The point
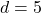 units,
units, 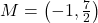
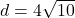 units,
units, 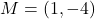
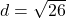 units,
units, 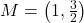
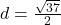 units,
units, 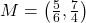
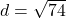 units,
units, 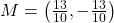
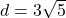 units,
units, 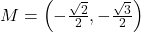
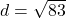 units,
units, 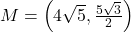
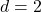 units,
units, 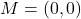
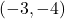 ,
, 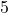 miles,
miles, 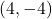
- The distance from
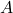 to
to 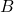 is
is 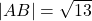 , the distance from
, the distance from 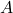 to
to 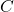 is
is 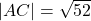 , and the distance from
, and the distance from 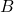 to
to 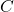 is
is 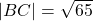 . because
. because 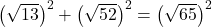 , we are guaranteed by the converse of the Pythagorean Theorem that the triangle is a right triangle.
, we are guaranteed by the converse of the Pythagorean Theorem that the triangle is a right triangle.
Section 1.2 Answers
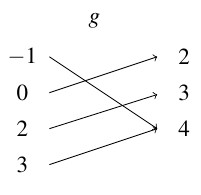
- The mapping
 is not a function because `Tennant’ is matched with both `Eleven’ and `Twelve.’
is not a function because `Tennant’ is matched with both `Eleven’ and `Twelve.’ - The mapping
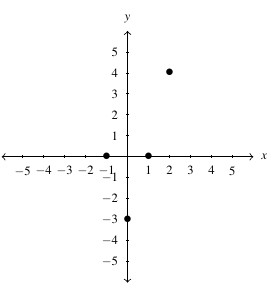
 is a function because each input is matched with only one output. The domain of
is a function because each input is matched with only one output. The domain of 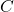 is
is 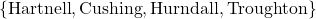 and the range is
and the range is 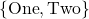 . We can represent
. We can represent  as the following set of ordered pairs:
as the following set of ordered pairs: 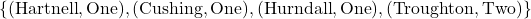
- In this case,
 is a function of
is a function of  because each
because each  is matched with only one
is matched with only one  .The domain is
.The domain is 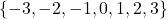 and the range is
and the range is 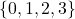 .As ordered pairs, this function is
.As ordered pairs, this function is 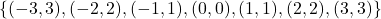
- In this case,
 is not a function of
is not a function of  because there are
because there are  values matched with more than one
values matched with more than one  value. For instance,
value. For instance, 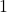 is matched both to
is matched both to 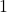 and
and 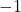 .
. - The mapping is a function because given any word, there is only one answer to `how many letters are in the word?’ For the range, we would need to know what the length of the longest word is and whether or not we could find words of all the lengths between
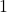 (the length of the word `a’) and it. See here.
(the length of the word `a’) and it. See here. - because Grover Cleveland was both the 22nd and 24th POTUS, neither mapping described in this exercise is a function.
- The outdoor temperature could never be the same for more than two different times – so, for example, it could always be getting warmer or it could always be getting colder.
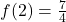 ,
, 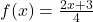
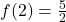 ,
, 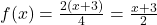
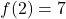 ,
, 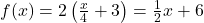
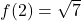 ,
, 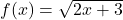
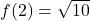 ,
, 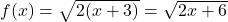
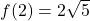 ,
, 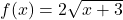
- For
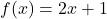
- For
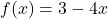
- For
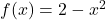
- For
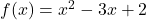
- For
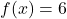
- For
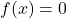
- For
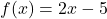
- For
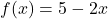
- For
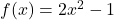
- For
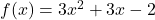
- For
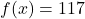
- For
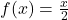
- For
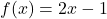 ,
, 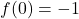 and
and 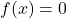 when
when 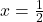
- For
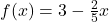 ,
, 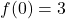 and
and 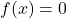 when
when 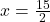
- For
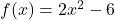 ,
, 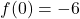 and
and 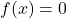 when
when 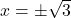
- For
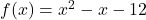 ,
, 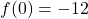 and
and 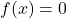 when
when 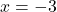 or
or 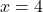
- Function
- Function
- Function
- Not a function
- Function
- Not a function
- Not a function
- Function
- Not a function
- Function
- Not a function
- Function
- Function
- Function
- Not a function
- Function, domain =
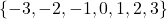 , range =
, range = 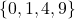
- Not a function
- Function, domain =
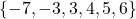 , range =
, range = 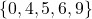
- Function, domain =
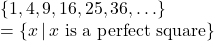 , range =
, range = 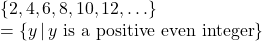
- Not a function
- Function, domain
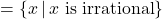 , range
, range 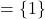
- Function, domain
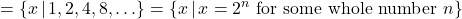 , range
, range 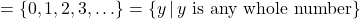
- Function, domain
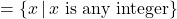 , range
, range 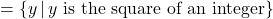
- Not a function
- Function, domain
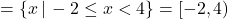 , range = \{
, range = \{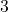 \}
\} - Function, domain
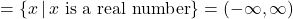 , range
, range 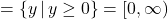
- Not a function
- Horizontal Line Test: A graph on the
 -plane represents
-plane represents  as a function of
as a function of  if and only if no horizontal line intersects the graph more than once.
if and only if no horizontal line intersects the graph more than once. - Function, domain =
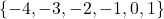 , range =
, range = 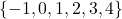
- Not a function
- Function, domain =
 , range =
, range = 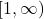
- Not a function
- .
- Number 58 represents
 as a function of
as a function of  , domain =
, domain = 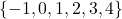 and range =
and range = 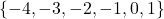
- Number 61 represents
 as a function of
as a function of  , domain =
, domain =  and range =
and range = 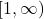
- Number 58 represents
- Function, domain =
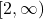 , range =
, range = 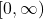
- Function, domain =
 , range =
, range = ![Rendered by QuickLaTeX.com (0, 4]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a7afbc956fa049963cd63baeff43019b_l3.png)
- Not a function
- Function, domain =
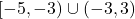 , range =
, range = 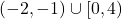
- Only number 63 represents
 as a function of
as a function of 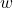 ; domain =
; domain = 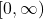 and range =
and range = 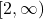
- Function, domain =
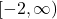 , range =
, range = 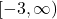
- Not a function
- Function, domain =
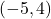 , range =
, range = 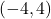
- Function , domain =
![Rendered by QuickLaTeX.com [0,3) \cup (3,6]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9cca553a690d5aa6cb00479a4c101c46_l3.png) , range =
, range = ![Rendered by QuickLaTeX.com (-4,-1] \cup [0,4]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9da1b8cebb6929e84526f580a91d4e24_l3.png)
- None of numbers 68 – 71 represent
 as a function of
as a function of 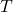 .
. - Function, domain =
 , range =
, range = ![Rendered by QuickLaTeX.com (-\infty, 4]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d97678af081b482ac4a03a2c3fb2b804_l3.png)
- Function, domain =
 , range =
, range = ![Rendered by QuickLaTeX.com (-\infty, 4]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d97678af081b482ac4a03a2c3fb2b804_l3.png)
- Function, domain =
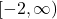 , range =
, range = ![Rendered by QuickLaTeX.com (-\infty, 3]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-3026892f9cf1442ab37da3e178e61a3e_l3.png)
- Function, domain =
 , range =
, range = 
- Only number 75 represents
 as a function of
as a function of 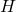 ; domain =
; domain = ![Rendered by QuickLaTeX.com (-\infty, 3]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-3026892f9cf1442ab37da3e178e61a3e_l3.png) and range =
and range = 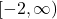
- Function, domain =
![Rendered by QuickLaTeX.com (-\infty, 0] \cup (1, \infty)](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-24e814f60a8eb110cac6d6f3d9be6e96_l3.png) , range =
, range = ![Rendered by QuickLaTeX.com (-\infty, 1] \cup \{ 2\}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a4dc5e1b63792e5afd7af57e07e3082c_l3.png)
- Function, domain =
![Rendered by QuickLaTeX.com [-3,3]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-78ea028c048c44b0799d326b85dd944f_l3.png) , range =
, range = ![Rendered by QuickLaTeX.com [-2,2]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b6a1d7a47c3d31f6cd1b1ec76d295f2c_l3.png)
- Not a function
- Function, domain =
 , range =
, range = 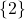
- Only number 80 represents
 as a function of
as a function of 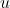 ; domain =
; domain =  and range=
and range=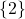
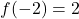
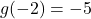
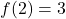
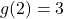
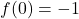
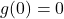
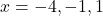
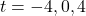
- Domain:
![Rendered by QuickLaTeX.com [-5,3]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c3b2c7b5023b5cba7c77dff383780891_l3.png) , Range:
, Range: ![Rendered by QuickLaTeX.com [-5,4]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-050a971431aa3500475d8615cddc6bda_l3.png)
- Domain:
![Rendered by QuickLaTeX.com [-4,4]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5a9ae584c04e4ba103a2782547a9c872_l3.png) , Range:
, Range: 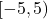
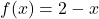 , Domain:
, Domain:  , Range:
, Range: 
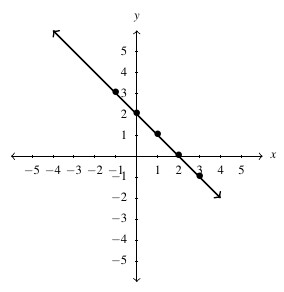
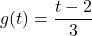 , Domain:
, Domain:  , Range:
, Range: 
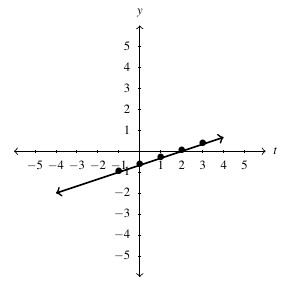
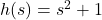 , Domain:
, Domain:  , Range:
, Range: 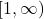
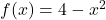 , Domain:
, Domain:  , Range:
, Range: ![Rendered by QuickLaTeX.com (-\infty, 4]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d97678af081b482ac4a03a2c3fb2b804_l3.png)
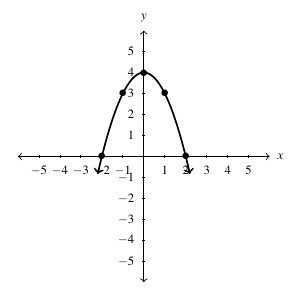
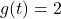 , Domain:
, Domain:  , Range:
, Range: 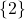
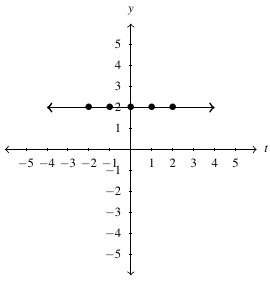
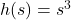 , Domain:
, Domain:  , Range:
, Range: 
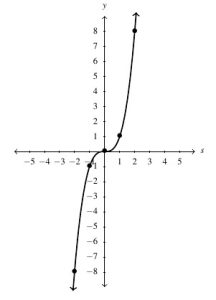
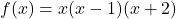 , Domain:
, Domain:  , Range:
, Range: 
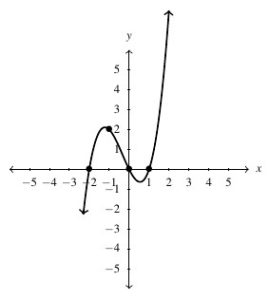
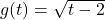 , Domain:
, Domain: 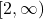 , Domain:
, Domain: 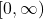
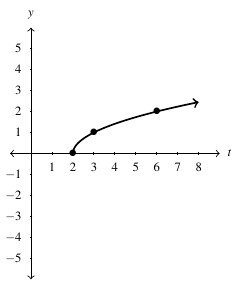
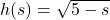 , Domain:
, Domain: ![Rendered by QuickLaTeX.com (-\infty, 5]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b7030f3f53b99ec89442a13dd3d9653d_l3.png) , Range:
, Range: 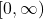
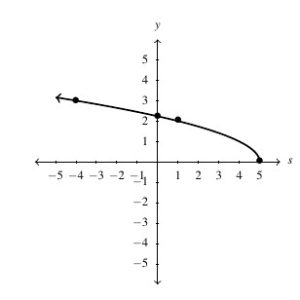
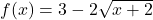 , Domain:
, Domain: 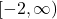 , Range:
, Range: ![Rendered by QuickLaTeX.com (-\infty, 3]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-3026892f9cf1442ab37da3e178e61a3e_l3.png)
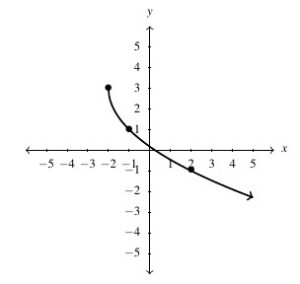
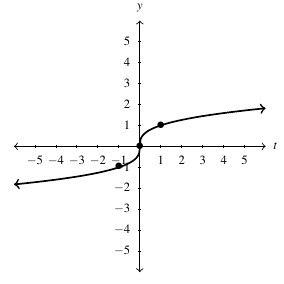
![Rendered by QuickLaTeX.com g(t) = \sqrt[3]{t}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7c7e24d89d18511552e695969d277dde_l3.png) , Domain:
, Domain:  , Range:
, Range: 
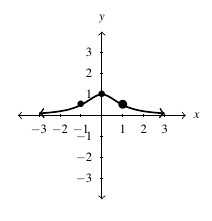
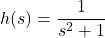 , Domain:
, Domain:  , Range:
, Range: ![Rendered by QuickLaTeX.com (0, 1]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-761bb18254850ccebdb04702cce64bfe_l3.png)
- .
- domain
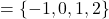 , range
, range 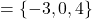
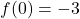 ,
, 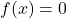 for
for 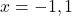
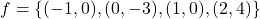
- domain
- .
- domain
 , range
, range 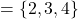
- Find
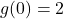 and
and 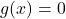 has no solutions.
has no solutions. 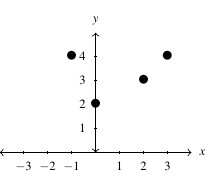
- domain
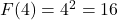 (when
(when 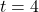 ), the solutions to
), the solutions to 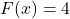 are
are 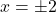 (when
(when 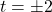 ).
).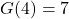 (when
(when 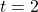 ), the solution to
), the solution to 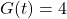 is
is 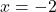 (when
(when 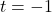 )
)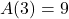 , so the area enclosed by a square with a side of length
, so the area enclosed by a square with a side of length 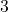 inches is
inches is 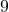 square inches. The solutions to
square inches. The solutions to 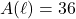 are
are 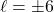 . because
. because 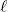 is restricted to
is restricted to 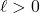 , we only keep
, we only keep 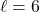 . This means for the area enclosed by the square to be
. This means for the area enclosed by the square to be 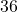 square inches, the length of the side needs to be
square inches, the length of the side needs to be 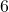 inches. because
inches. because 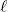 represents a length,
represents a length, 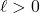 .
.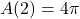 , so the area enclosed by a circle with radius
, so the area enclosed by a circle with radius 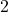 meters is
meters is 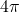 square meters. The solutions to
square meters. The solutions to 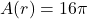 are
are 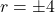 . because
. because  is restricted to
is restricted to 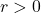 , we only keep
, we only keep 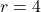 . This means for the area enclosed by the circle to be
. This means for the area enclosed by the circle to be 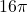 square meters, the radius needs to be
square meters, the radius needs to be 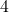 meters. because
meters. because  represents a radius (length),
represents a radius (length), 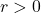 .
.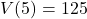 , so the volume enclosed by a cube with a side of length
, so the volume enclosed by a cube with a side of length 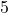 centimeters is
centimeters is 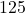 cubic centimeters. The solution to
cubic centimeters. The solution to 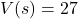 is
is 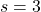 . This means for the volume enclosed by the cube to be
. This means for the volume enclosed by the cube to be 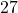 cubic centimeters, the length of the side needs to
cubic centimeters, the length of the side needs to 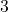 centimeters. because
centimeters. because  represents a length,
represents a length, 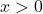 .
.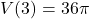 , so the volume enclosed by a sphere with radius
, so the volume enclosed by a sphere with radius 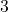 feet is
feet is 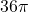 cubic feet. The solution to
cubic feet. The solution to 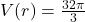 is
is 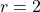 . This means for the volume enclosed by the sphere to be
. This means for the volume enclosed by the sphere to be 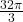 cubic feet, the radius needs to
cubic feet, the radius needs to 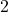 feet. because
feet. because  represents a radius (length),
represents a radius (length), 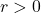 .
.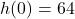 , so at the moment the object is dropped off the building, the object is
, so at the moment the object is dropped off the building, the object is 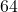 feet off of the ground. The solutions to
feet off of the ground. The solutions to 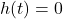 are
are 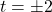 . because we restrict
. because we restrict 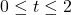 , we only keep
, we only keep 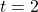 . This means
. This means 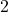 seconds after the object is dropped off the building, it is
seconds after the object is dropped off the building, it is 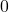 feet off the ground. Said differently, the object hits the ground after
feet off the ground. Said differently, the object hits the ground after 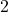 seconds. The restriction
seconds. The restriction 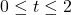 restricts the time to be between the moment the object is released and the moment it hits the ground.
restricts the time to be between the moment the object is released and the moment it hits the ground.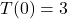 , so at 6 AM (
, so at 6 AM (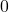 hours after 6 AM), it is
hours after 6 AM), it is 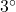 Fahrenheit.
Fahrenheit. 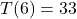 , so at noon (
, so at noon (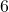 hours after 6 AM), the temperature is
hours after 6 AM), the temperature is 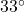 Fahrenheit.
Fahrenheit. 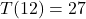 , so at 6 PM (
, so at 6 PM (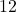 hours after 6 AM), it is
hours after 6 AM), it is 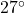 Fahrenheit.
Fahrenheit.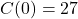 , so to make
, so to make 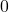 pens, it costs[1]
pens, it costs[1] 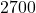 .
. 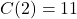 , so to make
, so to make 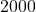 pens, it costs
pens, it costs 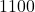 .
. 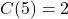 , so to make
, so to make 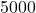 pens, it costs
pens, it costs 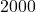 .
.- \item
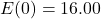 , so in 1980 (
, so in 1980 (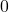 years after 1980), the average fuel economy of passenger cars in the US was
years after 1980), the average fuel economy of passenger cars in the US was 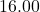 miles per gallon.
miles per gallon. 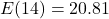 , so in 1994 (
, so in 1994 (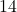 years after 1980), the average fuel economy of passenger cars in the US was
years after 1980), the average fuel economy of passenger cars in the US was 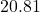 miles per gallon.
miles per gallon. 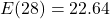 , so in 2008 (
, so in 2008 (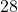 years after 1980), the average fuel economy of passenger cars in the US was
years after 1980), the average fuel economy of passenger cars in the US was 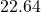 miles per gallon.
miles per gallon. 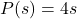 ,
, 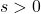 .
.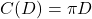 ,
, 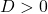 .
.- .
- The amount in the retirement account after 30 years if the monthly payment is
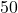 .
. - The solution to
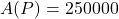 is what the monthly payment needs to be in order to have 250,000 dollars in the retirement account after 30 years.
is what the monthly payment needs to be in order to have 250,000 dollars in the retirement account after 30 years. 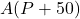 is how much is in the retirement account in 30 years if 50 dollars is added to the monthly payment
is how much is in the retirement account in 30 years if 50 dollars is added to the monthly payment 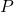 .
. 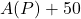 represents the amount of money in the retirement account after 30 years if
represents the amount of money in the retirement account after 30 years if 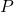 dollars is invested each month plus an additional
dollars is invested each month plus an additional 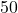 dollars.
dollars. 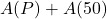 is the sum of money from two retirement accounts after 30 years: one with monthly payment
is the sum of money from two retirement accounts after 30 years: one with monthly payment 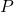 dollars and one with monthly payment
dollars and one with monthly payment 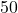 dollars.
dollars.
- The amount in the retirement account after 30 years if the monthly payment is
- .
- because noon is 4 hours after 8 AM,
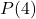 gives the chance of precipitation at noon.
gives the chance of precipitation at noon. - We would need to solve
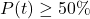 or
or 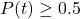 .
.
- because noon is 4 hours after 8 AM,
- The graph in question passes the horizontal line test meaning for each
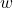 there is only one
there is only one  . The domain of
. The domain of  is
is 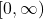 (which is the range of
(which is the range of  ) and the range of
) and the range of  is
is 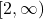 which is the domain of
which is the domain of  .
. - Answers vary.
Section 1.3 Answers
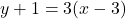 and
and 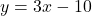
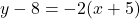 and
and 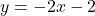
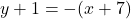 and
and 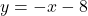
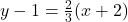 and
and 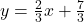
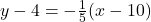 and
and 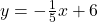
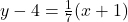 and
and 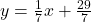
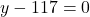 and
and 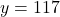
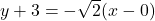 and
and 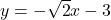
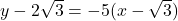 and
and 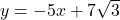
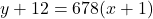 and
and 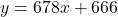
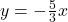
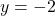
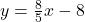
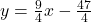
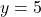
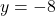
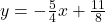
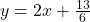
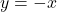
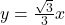
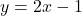 , slope:
, slope: 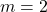 ,
,  -intercept:
-intercept: 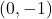 ,
,  -intercept:
-intercept: 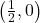
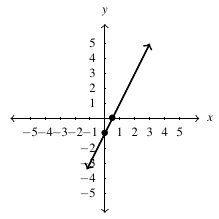
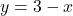 , slope:
, slope: 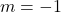 ,
,  -intercept:
-intercept: 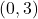 ,
,  -intercept:
-intercept: 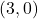
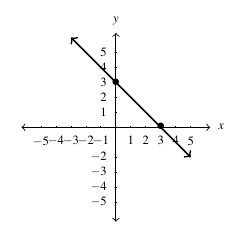
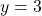 , slope:
, slope: 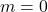 ,
,  -intercept:
-intercept: 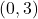 ,
,  -intercept: none
-intercept: none
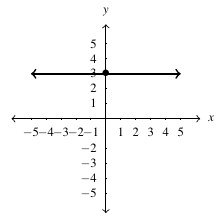
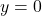 , slope:
, slope: 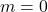 ,
,  -intercept:
-intercept: 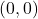 ,
,  -intercept:
-intercept: 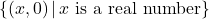
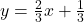 , slope:
, slope: 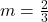 ,
,  -intercept:
-intercept: 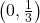 ,
,  -intercept:
-intercept: 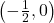
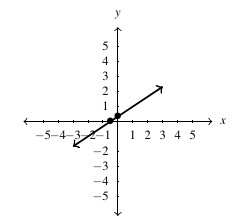
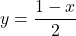 , slope:
, slope: 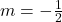 ,
,  -intercept:
-intercept: 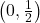 ,
,  -intercept:
-intercept: 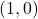
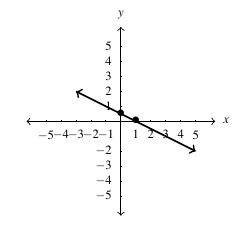
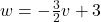 , slope:
, slope: 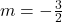 ,
, 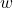 -intercept:
-intercept: 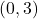 ,
,  -intercept:
-intercept: 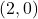
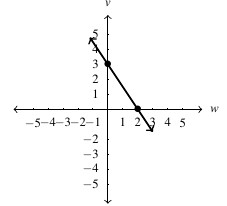
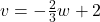 , slope:
, slope: 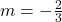 ,
,  -intercept:
-intercept: 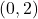 ,
, 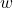 -intercept:
-intercept: 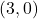
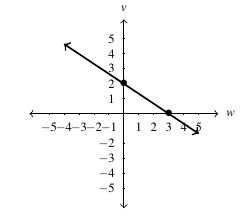
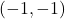 and
and 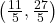
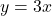
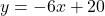
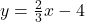
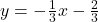
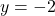
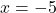
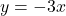
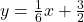
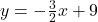
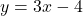
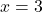
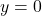
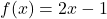 , slope:
, slope: 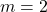 ,
,  -intercept:
-intercept: 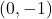 ,
,  -intercept:
-intercept: 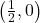

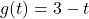 , slope:
, slope: 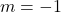 ,
,  -intercept:
-intercept: 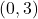 ,
,  -intercept:
-intercept: 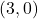

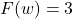 , slope:
, slope: 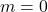 ,
,  -intercept:
-intercept: 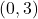 ,
, 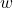 -intercept: none
-intercept: none

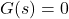 , slope:
, slope: 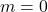 ,
,  -intercept:
-intercept: 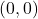 ,
,  -intercept:
-intercept: 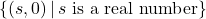

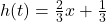 , slope:
, slope: 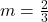 ,
,  -intercept:
-intercept: 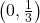 ,
,  -intercept:
-intercept: 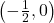

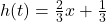 , slope:
, slope: 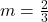 ,
,  -intercept:
-intercept: 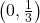 ,
,  -intercept:
-intercept: 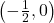

- domain:
 , range:
, range: 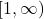 ,
,  -intercept:
-intercept: 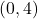 ,
,  -intercept: none
-intercept: none
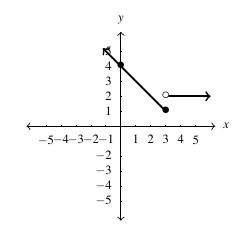
- domain:
 , range:
, range: 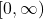 ,
,  -intercept:
-intercept: 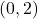 ,
,  -intercept:
-intercept: 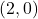
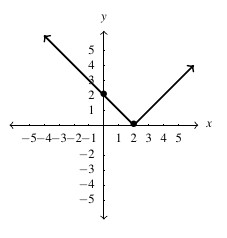
- domain:
 , range:
, range: 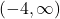 ,
,  -intercept:
-intercept: 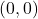 ,
,  -intercepts:
-intercepts: 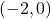 ,
, 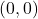
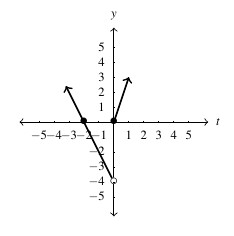
- domain:
 , range:
, range: ![Rendered by QuickLaTeX.com [-3, 3]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-851fff7eb0ecab039e6c3a74889d9a65_l3.png) ,
,  -intercept:
-intercept: 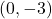 ,
,  -intercept:
-intercept: 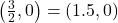
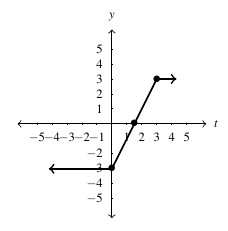
- .
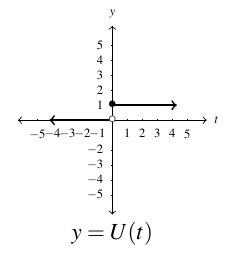
- domain:
 , range:
, range: 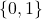
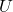 is constant on
is constant on 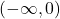 and
and 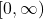 .
.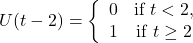
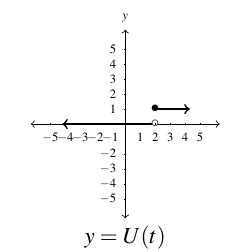
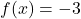
- This is called the `fixed' or `start-up' cost. We'll revisit this concept in Example 1.3.8 in Section 1.3.1. ↵

