1.1 Rectangular Coordinate Plane
1.1.1 The Cartesian Coordinate Plane
In order to visualize the pure excitement that is Precalculus, we need to unite Algebra and Geometry. Simply put, we must find a way to draw algebraic things. Let’s start with possibly the greatest mathematical achievement of all time: the Cartesian Coordinate Plane.[1] Imagine two real number lines crossing at a right angle at ![]() as drawn below.
as drawn below.
The horizontal number line is usually called the ![]() -axis while the vertical number line is usually called the
-axis while the vertical number line is usually called the ![]() -axis. As with things in the `real’ world, however, it’s best not to get too caught up with labels. Think of
-axis. As with things in the `real’ world, however, it’s best not to get too caught up with labels. Think of ![]() and
and ![]() as generic label placeholders, in much the same way as the variables
as generic label placeholders, in much the same way as the variables ![]() and
and ![]() are placeholders for real numbers. The letters we choose to identify with the axes depend on the context. For example, if we were plotting the relationship between time and the number of Sasquatch sightings, we might label the horizontal axis as the
are placeholders for real numbers. The letters we choose to identify with the axes depend on the context. For example, if we were plotting the relationship between time and the number of Sasquatch sightings, we might label the horizontal axis as the ![]() -axis (for `time’) and the vertical axis the
-axis (for `time’) and the vertical axis the ![]() -axis (for `number’ of sightings.) As with the usual number line, we imagine these axes extending off indefinitely in both directions.[2]
-axis (for `number’ of sightings.) As with the usual number line, we imagine these axes extending off indefinitely in both directions.[2]
Having two number lines allows us to locate the positions of points off of the number lines as well as points on the lines themselves. For example, consider the point ![]() on the next page. To use the numbers on the axes to label this point, we imagine dropping a vertical line from the
on the next page. To use the numbers on the axes to label this point, we imagine dropping a vertical line from the ![]() -axis to
-axis to ![]() and extending a horizontal line from the
and extending a horizontal line from the ![]() -axis to
-axis to ![]() . This process is sometimes called `projecting’ the point
. This process is sometimes called `projecting’ the point ![]() to the
to the ![]() – (respectively
– (respectively ![]() -) axis. We then describe the point
-) axis. We then describe the point ![]() using the ordered pair
using the ordered pair ![]() . The first number in the ordered pair is called the abscissa or
. The first number in the ordered pair is called the abscissa or ![]() -coordinate and the second is called the ordinate or
-coordinate and the second is called the ordinate or ![]() -coordinate. Again, the names of the coordinates can vary depending on the context of the application. If, as in the previous paragraph, the horizontal axis represented time and the vertical axis represented the number of Sasquatch sightings, the first coordinate would be called the
-coordinate. Again, the names of the coordinates can vary depending on the context of the application. If, as in the previous paragraph, the horizontal axis represented time and the vertical axis represented the number of Sasquatch sightings, the first coordinate would be called the ![]() -coordinate and the second coordinate would be the
-coordinate and the second coordinate would be the ![]() -coordinate. What’s important is that we maintain the convention that the abscissa (first coordinate) always corresponds to the horizontal position, while the ordinate (second coordinate) always corresponds to the vertical position. Taken together, the ordered pair
-coordinate. What’s important is that we maintain the convention that the abscissa (first coordinate) always corresponds to the horizontal position, while the ordinate (second coordinate) always corresponds to the vertical position. Taken together, the ordered pair ![]() comprise the Cartesian coordinates[3] of the point
comprise the Cartesian coordinates[3] of the point ![]() .
.
In practice, the distinction between a point and its coordinates is blurred; for example, we often speak of `the point ![]() ‘. We can think of
‘. We can think of ![]() as instructions on how to reach
as instructions on how to reach ![]() from the origin
from the origin ![]() by moving
by moving ![]() units to the right and
units to the right and ![]() units downwards. Notice that the order in the \underline{ordered} pair is important, as are the signs of the numbers in the pair. If we wish to plot the point
units downwards. Notice that the order in the \underline{ordered} pair is important, as are the signs of the numbers in the pair. If we wish to plot the point ![]() , we would move to the left
, we would move to the left ![]() units from the origin and then move upwards
units from the origin and then move upwards ![]() units, as below on the right.
units, as below on the right.

When we speak of the Cartesian Coordinate Plane, we mean the set of all possible ordered pairs ![]() as
as ![]() and
and ![]() take values from the real numbers. Below is a summary of some basic, but nonetheless important, facts about Cartesian coordinates.
take values from the real numbers. Below is a summary of some basic, but nonetheless important, facts about Cartesian coordinates.
Important Facts about the Cartesian Coordinate Plane
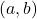 and
and 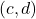 represent the same point in the plane if and only if
represent the same point in the plane if and only if  and
and 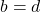 .
.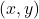 lies on the
lies on the  -axis if and only if
-axis if and only if 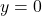 .
.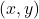 lies on the
lies on the  -axis if and only if
-axis if and only if 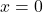 .
.- The origin is the point
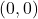 . It is the only point common to both axes.
. It is the only point common to both axes.
Example 1.1.1
Example 1.1.1
Plot the following points: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . (The letter
. (The letter ![]() is almost always reserved for the origin.)
is almost always reserved for the origin.)
Solution:
To plot these points, we start at the origin and move to the right if the ![]() -coordinate is positive; to the left if it is negative. Next, we move up if the
-coordinate is positive; to the left if it is negative. Next, we move up if the ![]() -coordinate is positive or down if it is negative. If the
-coordinate is positive or down if it is negative. If the ![]() -coordinate is
-coordinate is ![]() , we start at the origin and move along the
, we start at the origin and move along the ![]() -axis only. If the
-axis only. If the ![]() -coordinate is
-coordinate is ![]() we move along the
we move along the ![]() -axis only.
-axis only.
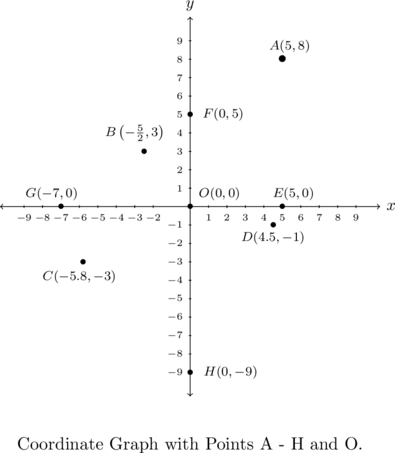
The axes divide the plane into four regions called quadrants. They are labeled with Roman numerals and proceed counterclockwise around the plane:

For example, ![]() lies in Quadrant I,
lies in Quadrant I, ![]() in Quadrant II,
in Quadrant II, ![]() in Quadrant III and
in Quadrant III and ![]() in Quadrant IV. If a point other than the origin happens to lie on the axes, we typically refer to that point as lying on the positive or negative
in Quadrant IV. If a point other than the origin happens to lie on the axes, we typically refer to that point as lying on the positive or negative ![]() -axis (if
-axis (if ![]() ) or on the positive or negative
) or on the positive or negative ![]() -axis (if
-axis (if ![]() ). For example,
). For example, ![]() lies on the positive
lies on the positive ![]() -axis whereas
-axis whereas ![]() lies on the negative
lies on the negative ![]() -axis. Such points do not belong to any of the four quadrants.
-axis. Such points do not belong to any of the four quadrants.
One of the most important concepts in all of Mathematics is symmetry. There are many types of symmetry in Mathematics, but three of them can be discussed easily using Cartesian Coordinates.
Definition 1.1
Two points ![]() and
and ![]() in the plane are said to be
in the plane are said to be
- symmetric about the
 -axis if
-axis if  and
and 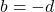
- symmetric about the
 -axis if
-axis if 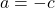 and
and 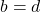
- symmetric about the origin if
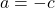 and
and 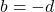
Schematically,
In the above figure, ![]() and
and ![]() are symmetric about the
are symmetric about the ![]() -axis, as are
-axis, as are ![]() and
and ![]() ;
; ![]() and
and ![]() are symmetric about the
are symmetric about the ![]() -axis, as are
-axis, as are ![]() and
and ![]() ; and
; and ![]() and
and ![]() are symmetric about the origin, as are
are symmetric about the origin, as are ![]() and
and ![]() .
.
Example 1.1.2
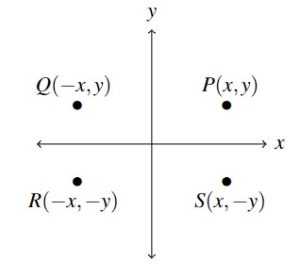
Example 1.1.2a
Let ![]() be the point
be the point ![]() . State the points which are symmetric to
. State the points which are symmetric to ![]() about the
about the ![]() -axis. Check your answer by plotting the points.
-axis. Check your answer by plotting the points.
Solution:
The figure after Definition 1.1 gives us a good way to think about finding symmetric points in terms of taking the opposites of the ![]() – and/or
– and/or ![]() -coordinates of
-coordinates of ![]() .
.
To find the point symmetric to point ![]() about the
about the ![]() -axis, we replace the
-axis, we replace the ![]() -coordinate of
-coordinate of ![]() with its opposite
with its opposite ![]() to get
to get ![]() .
.
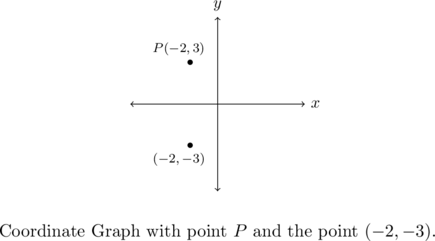
Example 1.1.2b
Let ![]() be the point
be the point ![]() . State the points which are symmetric to
. State the points which are symmetric to ![]() about the
about the ![]() -axis. Check your answer by plotting the points.
-axis. Check your answer by plotting the points.
Solution:
The figure after Definition 1.1 gives us a good way to think about finding symmetric points in terms of taking the opposites of the ![]() – and/or
– and/or ![]() -coordinates of
-coordinates of ![]() .
.
To find the point symmetric to point ![]() about the
about the ![]() -axis, we replace the
-axis, we replace the ![]() -coordinate of
-coordinate of ![]() with its opposite
with its opposite ![]() to get
to get ![]() .
.
Example 1.1.2c
Let ![]() be the point
be the point ![]() . State the points which are symmetric to
. State the points which are symmetric to ![]() about the origin. Check your answer by plotting the points.
about the origin. Check your answer by plotting the points.
Solution:
The figure after Definition 1.1 gives us a good way to think about finding symmetric points in terms of taking the opposites of the ![]() – and/or
– and/or ![]() -coordinates of
-coordinates of ![]() .
.
To find the point symmetric to point ![]() about the origin, we replace both the
about the origin, we replace both the ![]() – and
– and ![]() -coordinates with their opposites to get
-coordinates with their opposites to get ![]() .
.
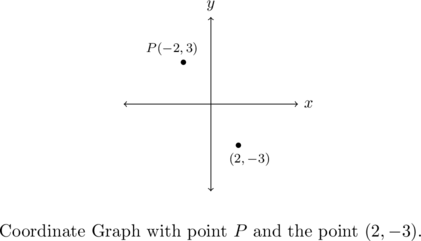
One way to visualize the processes in the previous example is with the concept of a reflection. If we start with our point ![]() and pretend that the
and pretend that the ![]() -axis is a mirror, then the reflection of
-axis is a mirror, then the reflection of ![]() across the
across the ![]() -axis would lie at
-axis would lie at ![]() . If we pretend that the
. If we pretend that the ![]() -axis is a mirror, the reflection of
-axis is a mirror, the reflection of ![]() across that axis would be
across that axis would be ![]() . If we reflect across the
. If we reflect across the ![]() -axis and then the
-axis and then the ![]() -axis, we would go from
-axis, we would go from ![]() to
to ![]() then to
then to ![]() , and so we would end up at the point symmetric to
, and so we would end up at the point symmetric to ![]() about the origin. We summarize and generalize this process below.
about the origin. We summarize and generalize this process below.
Reflections
To reflect a point ![]() about the:
about the:
 -axis, replace
-axis, replace  with
with 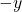 .
. -axis, replace
-axis, replace  with
with 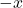 .
.- origin, replace
 with
with 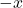 and
and  with
with 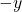 .
.
1.1.2 Distance in the Plane
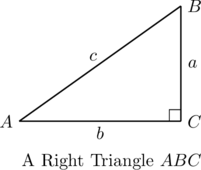
Another fundamental concept in Geometry is the notion of length. If we are going to unite Algebra and Geometry using the Cartesian Plane, then we need to develop an algebraic understanding of what distance in the plane means. Before we can do that, we need to state what we believe is the most important theorem in all of Geometry: The Pythagorean Theorem.
The theorem actually says two different things. If we know that ![]() then the angle
then the angle ![]() must be a right angle. If we know geometrically that
must be a right angle. If we know geometrically that ![]() is already a right angle then we have that
is already a right angle then we have that ![]() . We need the latter statement in the discussion which follows.
. We need the latter statement in the discussion which follows.
Suppose we have two points, ![]() and
and ![]() in the plane. By the distance
in the plane. By the distance ![]() between
between ![]() and
and ![]() , we mean the length of the line segment joining
, we mean the length of the line segment joining ![]() with
with ![]() . (Remember, given any two distinct points in the plane, there is a unique line containing both points.) Our goal now is to create an algebraic formula to compute the distance between these two points. Consider the generic situation below on the left.
. (Remember, given any two distinct points in the plane, there is a unique line containing both points.) Our goal now is to create an algebraic formula to compute the distance between these two points. Consider the generic situation below on the left.
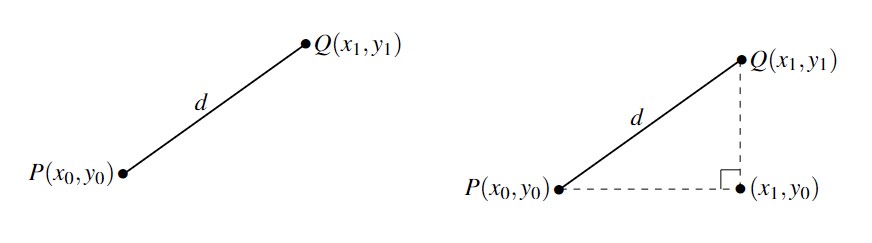
With a little more imagination, we can envision a right triangle whose hypotenuse has length ![]() as drawn above on the right. From the latter figure, we see that the lengths of the legs of the triangle are
as drawn above on the right. From the latter figure, we see that the lengths of the legs of the triangle are ![]() and
and ![]() so the Pythagorean Theorem gives us
so the Pythagorean Theorem gives us
![]()
![]()
(Do you remember why we can replace the absolute value notation with parentheses?) By extracting the square root of both sides of the second equation and using the fact that distance is never negative, we get
A couple of remarks about Equation 1.1 are in order. First, it is not always the case that the points ![]() and
and ![]() lend themselves to constructing such a triangle. If the points
lend themselves to constructing such a triangle. If the points ![]() and
and ![]() are arranged vertically or horizontally, or describe the exact same point, we cannot use the above geometric argument to derive the distance formula. Second, distance is a `length’. So, technically, the number we obtain from the distance formula has some attached units of length. In this text, we’ll adopt the convention that the phrase `units’ refers to some generic units of length.[4] Our next example gives us an opportunity to test drive the distance formula as well as brush up on some arithmetic and prerequisite algebra.
are arranged vertically or horizontally, or describe the exact same point, we cannot use the above geometric argument to derive the distance formula. Second, distance is a `length’. So, technically, the number we obtain from the distance formula has some attached units of length. In this text, we’ll adopt the convention that the phrase `units’ refers to some generic units of length.[4] Our next example gives us an opportunity to test drive the distance formula as well as brush up on some arithmetic and prerequisite algebra.
Example 1.1.3
Example 1.1.3a
Compute and simplify the distance between the following sets of points:
![]() and
and ![]()
Solution:
Compute the distance between ![]() and
and ![]() .
.
In each case, we apply the distance formula, Equation 1.1 with the first point listed taken as ![]() and the second point taken as
and the second point taken as ![]() .[5]
.[5]
With ![]() and
and ![]() , we get
, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} d & = & \sqrt{\left(x_{1} - x_{0} \right)^2 + \left(y_{1} - y_{0} \right)^2} & \\[8pt] & = & \sqrt{ (1-(-2))^2 + (-3-3)^2} & \\[8pt] & = & \sqrt{9 + 36} & \\[8pt] & = & \sqrt{45} & \\[8pt] & = & \sqrt{9 \cdot 5} & \\[8pt] & = & \sqrt{9} \sqrt{5} & \text{For nonnegative numbers, } \sqrt{ab} = \sqrt{a} \sqrt{b}. \\[8pt] & = & 3 \sqrt{5} & \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-1a9ca2d8c0e81e325e8b07cf0fa10aa1_l3.png)
So the distance between ![]() and
and ![]() is
is ![]() units.
units.
Example 1.1.3b
Compute and simplify the distance between the following sets of points:
![]() and
and ![]() .
.
Solution:
Compute the distance between ![]() and
and ![]() .
.
In each case, we apply the distance formula, Equation 1.1 with the first point listed taken as ![]() and the second point taken as
and the second point taken as ![]() . With
. With ![]() and
and ![]() , we get
, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} d & = & \sqrt{\left(x_{1} - x_{0} \right)^2 + \left(y_{1} - y_{0} \right)^2} & \\[8pt] & = & \sqrt{ \left(\frac{3}{4}-\frac{1}{2} \right)^2 + \left(\frac{1}{5} - \frac{2}{3} \right)^2} & \text{Get common denominators to add and subtract fractions.}\\[8pt] & = & \sqrt{\left(\frac{1}{4} \right)^2 + \left(-\frac{7}{15} \right)^2} &\\[8pt] & = & \sqrt{\frac{1}{16} + \frac{49}{225}} & \text{ Because } \left(\frac{a}{b}\right)^2 = \frac{a^2}{b^2}, \, b \neq 0.\\[8pt] & = & \sqrt{\frac{1009}{3600}} & \\[8pt] & = & \frac{\sqrt{1009}}{\sqrt{3600}} & \\ & = & \frac{\sqrt{1009}}{60} & \text{For nonnegative numbers, } \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}, \, b \neq 0. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-30351c7db845eade74550dbd5647858a_l3.png)
So the distance ![]() and
and ![]() is
is ![]() units.
units.
Example 1.1.3c
Compute and simplify the distance between the following sets of points:
![]() and
and ![]() .
.
Solution:
Compute the distance between ![]() and
and ![]() .
.
In each case, we apply the distance formula, Equation 1.1 with the first point listed taken as ![]() and the second point taken as
and the second point taken as ![]() . With
. With ![]() and
and ![]() , we get
, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} d & = & \sqrt{\left(x_{1} - x_{0} \right)^2 + \left(y_{1} - y_{0} \right)^2} & \\[8pt] & = & \sqrt{ \left(\sqrt{12}- \sqrt{3} \right)^2 + \left(\sqrt{5} - (-\sqrt{20})\right)^2} & \\[8pt] & = & \sqrt{\left(2\sqrt{3} - \sqrt{3} \right)^2 + \left(\sqrt{5}+2\sqrt{5} \right)^2} & \text{Simplify the radicals to get like terms.}\\[8pt] & = & \sqrt{\left(\sqrt{3}\right)^2 + \left(3 \sqrt{5}\right)^2} & \\[8pt] & = & \sqrt{3 + 9 \cdot 5} & \text{Given } (\sqrt{a})^2 = a \text{ and } (b \sqrt{a})^2 = b^2 (\sqrt{a})^2. \\ & = & \sqrt{48} & \\ & = & 4\sqrt{3} & \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5817bba0d8c9c6bf1c46113c079fddbe_l3.png)
So the distance between ![]() and
and ![]() is
is ![]() units.
units.
Example 1.1.3d
Compute and simplify the distance between the following sets of points:
![]() and
and ![]() .
.
Solution:
Compute the distance between ![]() and
and ![]() .
.
In each case, we apply the distance formula, Equation 1.1 with the first point listed taken as ![]() and the second point taken as
and the second point taken as ![]() . With
. With ![]() and
and ![]() , we get
, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} d & = & \sqrt{\left(x_{1} - x_{0} \right)^2 + \left(y_{1} - y_{0} \right)^2} & \\[8pt] & = & \sqrt{ \left(x- 0\right)^2 + \left(y - 0\right)^2} & \\[8pt] & = & \sqrt{x^2+y^2} & \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-09d1628e81463ddb00a889a048215601_l3.png)
As tempting as it may look, ![]() does not, in general, reduce to
does not, in general, reduce to ![]() or even
or even ![]() . So, in this case, the best we can do is state that the distance between
. So, in this case, the best we can do is state that the distance between ![]() and
and ![]() is
is ![]() units.
units.
Related to finding the distance between two points is the problem of finding the midpoint of the line segment connecting two points. Given two points, ![]() and
and ![]() , the midpoint
, the midpoint ![]() of
of ![]() and
and ![]() is defined to be the point on the line segment connecting
is defined to be the point on the line segment connecting ![]() and
and ![]() whose distance from
whose distance from ![]() is equal to its distance from
is equal to its distance from ![]() .
.
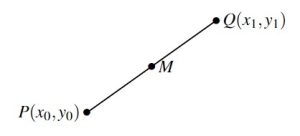
If we think of reaching ![]() by going `halfway over’ and `halfway up’ we get the following formula.
by going `halfway over’ and `halfway up’ we get the following formula.
If we let ![]() denote the distance between
denote the distance between ![]() and
and ![]() , we leave it to the reader to show that the distance between
, we leave it to the reader to show that the distance between ![]() and
and ![]() is
is ![]() which is the same as the distance between
which is the same as the distance between ![]() and
and ![]() . This suffices to show that Equation 1.2 gives the coordinates of the midpoint.
. This suffices to show that Equation 1.2 gives the coordinates of the midpoint.
Example 1.1.4
Example 1.1.4a
Determine the midpoint, ![]() , of the line segment connecting the following pairs of points:
, of the line segment connecting the following pairs of points:
![]() and
and ![]()
Solution:
Determine the midpoint of the line segment connecting ![]() and
and ![]() .
.
As with Example 1.1.3, in each case, we apply the midpoint formula, Equation 1.2, with the first point listed taken as ![]() and the second point taken as
and the second point taken as ![]() .[6] We also note that midpoints are points which means all of our answers should be ordered pairs.
.[6] We also note that midpoints are points which means all of our answers should be ordered pairs.
With ![]() and
and ![]() , we get
, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} M & = & \left( \dfrac{x_{0}+x_{1}}{2}, \dfrac{y_{0}+y_{1}}{2} \right) \\ & = & \left( \dfrac{(-2)+1}{2}, \dfrac{3+(-3)}{2} \right) \\ & = & \left(- \dfrac{1}{2}, 0 \right) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5cbf8c31b075f6d4a74851862ab04059_l3.png)
The midpoint of the line segment connecting ![]() and
and ![]() is
is ![]() .
.
Example 1.1.4b
Determine the midpoint, ![]() , of the line segment connecting the following pairs of points:
, of the line segment connecting the following pairs of points:
![]() and
and ![]()
Solution:
Determine the midpoint of the line segment connecting ![]() and
and ![]() .
.
In each case, we apply the midpoint formula, Equation 1.2, with the first point listed taken as ![]() and the second point taken as
and the second point taken as ![]() . With
. With ![]() and
and ![]() , we get
, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} M & = & \left( \dfrac{x_{0}+x_{1}}{2}, \dfrac{y_{0}+y_{1}}{2} \right) & \\[5pt] & = & \left( \dfrac{\frac{1}{2} + \frac{3}{4}}{2}, \dfrac{\frac{2}{3} + \frac{1}{5}}{2} \right) & \\[5pt] & = & \left( \dfrac{\left(\frac{1}{2} + \frac{3}{4}\right) \cdot 4}{2 \cdot 4}, \dfrac{\left(\frac{2}{3} + \frac{1}{5}\right) \cdot 15}{2 \cdot 15} \right) & \text{Simplify compound fractions.} \\ & = & \left(\dfrac{5}{8}, \dfrac{13}{30} \right) & \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-cf5a6d417d708fe3d168cf0f7ad6a05e_l3.png)
The midpoint of the line segment connecting ![]() and
and ![]() is
is ![]() .
.
Example 1.1.4c
Determine the midpoint, ![]() , of the line segment connecting the following pairs of points:
, of the line segment connecting the following pairs of points:
![]() and
and ![]()
Solution:
Determine the midpoint of the line segment connecting ![]() and
and ![]() .
.
In each case, we apply the midpoint formula, Equation 1.2, with the first point listed taken as ![]() and the second point taken as
and the second point taken as ![]() . With
. With ![]() and
and ![]() , we get
, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} M & = & \left( \dfrac{x_{0}+x_{1}}{2}, \dfrac{y_{0}+y_{1}}{2} \right) & \\ & = & \left( \dfrac{\sqrt{3} + \sqrt{12}}{2}, \dfrac{-\sqrt{20}+\sqrt{5}}{2} \right) & \\ & = & \left( \dfrac{\sqrt{3}+2\sqrt{3}}{2}, \dfrac{-2\sqrt{5} + \sqrt{5}}{2} \right) & \text{Simplify radicals to get like terms.} \\ & = & \left(\dfrac{3\sqrt{3}}{2}, -\dfrac{\sqrt{5}}{2} \right) & \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-ed5bd1f358ebe57134ef59b2baee1d5e_l3.png)
The midpoint of the line segment connecting ![]() and
and ![]() is
is ![]() .
.
Example 1.1.4d
Determine the midpoint, ![]() , of the line segment connecting the following pairs of points:
, of the line segment connecting the following pairs of points:
![]() and
and ![]()
Solution:
Determine the midpoint of the line segment connecting ![]() and
and ![]() .
.
In each case, we apply the midpoint formula, Equation 1.2, with the first point listed taken as ![]() and the second point taken as
and the second point taken as ![]() . With
. With ![]() and
and ![]() , we get
, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} M & = & \left( \dfrac{x_{0}+x_{1}}{2}, \dfrac{y_{0}+y_{1}}{2} \right) & \\ & = & \left( \dfrac{x+0}{2}, \dfrac{y+0}{2} \right) & \\ & = & \left( \dfrac{x}{2}, \dfrac{y}{2} \right) & \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-1f85c7632b68cdeec29f925e5e8b04a1_l3.png)
The midpoint of the line segment connecting ![]() and
and ![]() is
is ![]() .
.
We close with a more abstract application of the Midpoint Formula.
Example 1.1.5
Example 1.1.5
If ![]() , show that the line
, show that the line ![]() equally divides the line segment with endpoints
equally divides the line segment with endpoints ![]() and
and ![]() .
.
Solution:
To prove the claim, we use Equation 1.2 to find the midpoint
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} M & = & \left( \dfrac{a+b}{2}, \dfrac{b+a}{2} \right) \\ & = & \left( \dfrac{a+b}{2}, \dfrac{a+b}{2} \right) \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e610d326ea03b376fda6e114f97af2b8_l3.png)
As the ![]() and
and ![]() coordinates of this point are the same, we find that the midpoint lies on the line
coordinates of this point are the same, we find that the midpoint lies on the line ![]() , as required.
, as required.
1.1.3 Section Exercises
- Plot and label the points
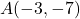 ,
, 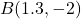 ,
, 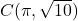 ,
, 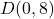 ,
, 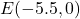 ,
, 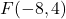 ,
, 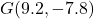 and
and 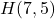 in the Cartesian Coordinate Plane.
in the Cartesian Coordinate Plane. - For each point given in Exercise 1 above
- Identify the quadrant or axis in/on which the point lies.
- Find the point symmetric to the given point about the
 -axis.
-axis. - Find the point symmetric to the given point about the
 -axis.
-axis. - Find the point symmetric to the given point about the origin.
In Exercises 3 – 10, compute the distance, ![]() , between the two given points and the midpoint
, between the two given points and the midpoint ![]() of the line segment which connects the two points.
of the line segment which connects the two points.
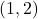 ,
, 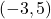
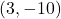 ,
, 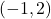
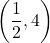 ,
, 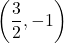
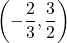 ,
, 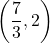
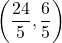 ,
, 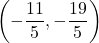
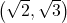 ,
, 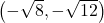
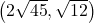 ,
, 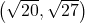
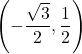 ,
, 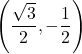
- Let’s assume that we are standing at the origin and the positive
 -axis points due North while the positive
-axis points due North while the positive  -axis points due East. Our Sasquatch-o-meter tells us that Sasquatch is 3 miles West and 4 miles South of our current position. What are the coordinates of his position? How far away is he from us? If he runs 7 miles due East what would his new position be?
-axis points due East. Our Sasquatch-o-meter tells us that Sasquatch is 3 miles West and 4 miles South of our current position. What are the coordinates of his position? How far away is he from us? If he runs 7 miles due East what would his new position be? - Show that the points
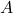 ,
, 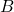 , and
, and 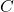 below are the vertices of a right triangle.
below are the vertices of a right triangle.
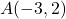 ,
, 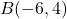 , and
, and 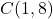
Section 1.1 Exercise Answers can be found in the Appendix … Coming soon
- So named in honor of Renè Descartes. ↵
- Usually extending off towards infinity is indicated by arrows, but here, the arrows are used to indicate the direction of increasing values of
 and
and  . ↵
. ↵ - Also called the `rectangular coordinates' of
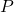 . ↵
. ↵ - As a result, we'll measure area with `square units,' or units
 and volume with `cubic units,' or units
and volume with `cubic units,' or units . ↵
. ↵ - This choice is completely arbitrary. The reader is encouraged to work these examples taking the first point listed as
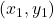 and the second point listed as
and the second point listed as 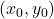 and verifying the distance works out to be the same. Can you see why the order of the subtraction in Equation 1.1 ultimately doesn't matter? ↵
and verifying the distance works out to be the same. Can you see why the order of the subtraction in Equation 1.1 ultimately doesn't matter? ↵ - As in Example 1.1.3, this choice is also completely arbitrary. The reader is encouraged to work these examples taking the first point listed as
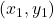 and the second point listed as
and the second point listed as 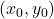 and verifying the midpoint works out to be the same. Can you see why the order of the points in Equation 1.2 doesn't matter? ↵
and verifying the midpoint works out to be the same. Can you see why the order of the points in Equation 1.2 doesn't matter? ↵
The first number in an ordered pair
The second number in an ordered pair
The point on the graph of the Cartesian Plane at the intersection of the horizontal and vertical axes, (0,0).
The midpoint of a line segment is the point on the line segment whose distance from each end of the segment is the same