1.2 Relations and Functions
Mathematics can be thought of as the study of patterns. In most disciplines, Mathematics is used as a language to express, or codify, relationships between quantities – both algebraically and geometrically – with the ultimate goal of solving real-world problems. The fact that the same algebraic equation which models the growth of bacteria in a petri dish is also used to compute the account balance of a savings account or the potency of radioactive material used in medical treatments speaks to the universal nature of Mathematics. Indeed, Mathematics is more than just about solving a specific problem in a specific situation, it’s about abstracting problems and creating universal tools which can be used by a variety of scientists and engineers to solve a variety of problems.
This power of abstraction has a tendency to create a language that is initially intimidating to students. Mathematical definitions are precise and adherence to that precision is often a source of confusion and frustration. It doesn’t help matters that more often than not very common words are used in Mathematics with slightly different definitions than is commonly expected.
In this section, we will study general mappings called relations. Then we will turn our focus to a special kind of mapping called functions.
Definition 1.2
Given two sets ![]() and
and ![]() , a relation from
, a relation from ![]() to
to ![]() is a process by which elements of
is a process by which elements of ![]() are matched with (or `mapped to’) elements of
are matched with (or `mapped to’) elements of ![]() .
.
1.2.1 Functions as Mappings
The first `universal tool’ we wish to highlight – the concept of a `function’ – is a perfect example of this phenomenon in that we redefine a word that already has multiple meanings in English.
Definition 1.3
Given two sets[1] ![]() and
and ![]() , a function from
, a function from ![]() to
to ![]() is a process by which each element of
is a process by which each element of ![]() is matched with (or `mapped to’) one and only one element of
is matched with (or `mapped to’) one and only one element of ![]() .
.
The grammar here `from ![]() to
to ![]() ‘ is important. Thinking of a function as a process, we can view the elements of the set
‘ is important. Thinking of a function as a process, we can view the elements of the set ![]() as our starting materials, or inputs to the process. The function processes these inputs according to some specified rule and the result is a set of outputs – elements of the set
as our starting materials, or inputs to the process. The function processes these inputs according to some specified rule and the result is a set of outputs – elements of the set ![]() . In terms of inputs and outputs, Definition 1.3 says that a function is a process in which each input is matched to one and only one output.
. In terms of inputs and outputs, Definition 1.3 says that a function is a process in which each input is matched to one and only one output.
For example, let’s take a look at some of the pets in the Stitz household. Taylor’s pets include White Paw and Cooper (both cats), Bingo (a lizard) and Kennie (a turtle). Let ![]() be the set of pet names:
be the set of pet names: ![]() , and let
, and let ![]() be the set of pet types:
be the set of pet types: ![]() . Let
. Let ![]() be the process that takes each pet’s name as the input and returns that pet’s type as the output. Let
be the process that takes each pet’s name as the input and returns that pet’s type as the output. Let ![]() be the reverse of
be the reverse of ![]() : that is,
: that is, ![]() takes each pet type as the input and returns the names of the pets of that type as the output. Note that both
takes each pet type as the input and returns the names of the pets of that type as the output. Note that both ![]() and
and ![]() are codifying the same given information about Taylor’s pets, but one of them is a function and the other is not.
are codifying the same given information about Taylor’s pets, but one of them is a function and the other is not.
To help identify which process ![]() or
or ![]() is a function and why the other is not, we create mapping diagrams for
is a function and why the other is not, we create mapping diagrams for ![]() and
and ![]() below. In each case, we organize the inputs in a column on the left and the outputs on a column on the right. We draw an arrow connecting each input to its corresponding output(s). Note that the arrows communicate the grammatical bias: the arrow originates at the input and points to the output.
below. In each case, we organize the inputs in a column on the left and the outputs on a column on the right. We draw an arrow connecting each input to its corresponding output(s). Note that the arrows communicate the grammatical bias: the arrow originates at the input and points to the output.

The process ![]() is a function because
is a function because ![]() matches each of its inputs (each pet name) to just one output (the pet’s type). The fact that different inputs (White Paw and Cooper) are matched to the same output (cat) is fine. On the other hand,
matches each of its inputs (each pet name) to just one output (the pet’s type). The fact that different inputs (White Paw and Cooper) are matched to the same output (cat) is fine. On the other hand, ![]() matches the input `cat’ to the two different outputs `White Paw’ and `Cooper’, so
matches the input `cat’ to the two different outputs `White Paw’ and `Cooper’, so ![]() is not a function. Functions are favored in mathematical circles because they are processes which produce only one answer (output) for any given query (input). In this scenario, for instance, there is only one answer to the question: `What type of pet is White Paw?’ but there is more than one answer to the question `Which of Taylor’s pets are cats?’
is not a function. Functions are favored in mathematical circles because they are processes which produce only one answer (output) for any given query (input). In this scenario, for instance, there is only one answer to the question: `What type of pet is White Paw?’ but there is more than one answer to the question `Which of Taylor’s pets are cats?’
As you might expect, with functions being such an important concept in Mathematics, we need to build a vocabulary to assist us when discussing them. To that end, we have the following definitions.[2]
Definition 1.4
Suppose ![]() is a function from
is a function from ![]() to
to ![]() .
.
- If
 , we write
, we write 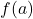 (read `
(read ` of
of  ‘) to denote the unique element of
‘) to denote the unique element of 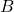 to which
to which  matches
matches  .
.
That is, if we view ` ‘ as the input to
‘ as the input to  , then `
, then `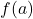 ‘ is the output from
‘ is the output from  .
. - The set
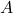 is called the domain.
is called the domain.
Said differently, the domain of a function is the set of inputs to the function. - The set
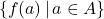 is called the range of
is called the range of  .
.
Said differently, the range of a function is the set of outputs from the function.
Some remarks about Definition 1.4 are in order. First, and most importantly, the notation `![]() ‘ in Definition 1.4 introduces yet another mathematical use for parentheses. Parentheses are used in some cases as grouping symbols, to represent ordered pairs, and to delineate intervals of real numbers. More often than not, the use of parentheses in expressions like `
‘ in Definition 1.4 introduces yet another mathematical use for parentheses. Parentheses are used in some cases as grouping symbols, to represent ordered pairs, and to delineate intervals of real numbers. More often than not, the use of parentheses in expressions like `![]() ‘ is confused with multiplication. As always, paying attention to the context is key. If
‘ is confused with multiplication. As always, paying attention to the context is key. If ![]() is a function and `
is a function and `![]() ‘ is in the domain of
‘ is in the domain of ![]() , then `
, then `![]() ‘ is the output from
‘ is the output from ![]() when you input
when you input ![]() . The diagram below provides a nice generic picture to keep in mind when thinking of a function as a mapping process with input `
. The diagram below provides a nice generic picture to keep in mind when thinking of a function as a mapping process with input `![]() ‘ and output `
‘ and output `![]() ‘.
‘.
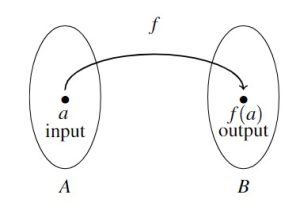
In the preceding pet example, the symbol ![]() , read `
, read `![]() of Bingo’, is asking what type of pet Bingo is, so
of Bingo’, is asking what type of pet Bingo is, so ![]() lizard. The fact that
lizard. The fact that ![]() is a function means
is a function means ![]() is unambiguous because
is unambiguous because ![]() matches the name `Bingo’ to only one pet type, namely `lizard’. In contrast, if we tried to use the notation `
matches the name `Bingo’ to only one pet type, namely `lizard’. In contrast, if we tried to use the notation `![]() ‘ to indicate what pet name
‘ to indicate what pet name ![]() matched to `cat’, we have two possibilities, White Paw and Cooper, with no way to determine which one (or both) is indicated.
matched to `cat’, we have two possibilities, White Paw and Cooper, with no way to determine which one (or both) is indicated.
Continuing to apply Definition 1.4 to our pet example, we find that the domain of the function ![]() is
is ![]() , the set of pet names. Finding the range takes a little more work, mostly because it’s easy to be caught off guard by the notation used in the definition of `range’. The description of the range as `
, the set of pet names. Finding the range takes a little more work, mostly because it’s easy to be caught off guard by the notation used in the definition of `range’. The description of the range as `![]() ‘ is an example of `set-builder’ notation. In English, `
‘ is an example of `set-builder’ notation. In English, `![]() ‘ reads as `the set of
‘ reads as `the set of ![]() such that
such that ![]() is in
is in ![]() ‘. In other words, the range consists of all of the outputs from
‘. In other words, the range consists of all of the outputs from ![]() – all of the
– all of the ![]() values – as
values – as ![]() varies through each of the elements in the domain
varies through each of the elements in the domain ![]() . Note that while every element of the set
. Note that while every element of the set ![]() is, by definition, an element of the domain of
is, by definition, an element of the domain of ![]() , not every element of the set
, not every element of the set ![]() is necessarily part of the range of
is necessarily part of the range of ![]() .[3]
.[3]
In our pet example, we can obtain the range of ![]() by looking at the mapping diagram or by constructing the set
by looking at the mapping diagram or by constructing the set ![]() which lists all of the outputs from
which lists all of the outputs from ![]() as we run through all of the inputs to
as we run through all of the inputs to ![]() . Keep in mind that we list each element of a set only once so the range of
. Keep in mind that we list each element of a set only once so the range of ![]() is:[4]
is:[4]
![]()
If we let ![]() denote a generic element of
denote a generic element of ![]() then
then ![]() is some element
is some element ![]() in
in ![]() , so we write
, so we write ![]() . In this equation,
. In this equation, ![]() is called the independent variable and
is called the independent variable and ![]() is called the dependent variable.[5] Moreover, we say `
is called the dependent variable.[5] Moreover, we say `![]() is a function of
is a function of ![]() ‘, or, more specifically, `the type of pet is a function of the pet name’ meaning that every pet name
‘, or, more specifically, `the type of pet is a function of the pet name’ meaning that every pet name ![]() corresponds to one, and only one, pet type
corresponds to one, and only one, pet type ![]() . Even though
. Even though ![]() and
and ![]() are different things,[6] it is very common for the function and its outputs to become more-or-less synonymous, even in what are otherwise precise mathematical definitions.[7] We will endeavor to point out such ambiguities as we move through the text.
are different things,[6] it is very common for the function and its outputs to become more-or-less synonymous, even in what are otherwise precise mathematical definitions.[7] We will endeavor to point out such ambiguities as we move through the text.
While the concept of a function is very general in scope, we will be focusing primarily on functions of real numbers because most disciplines use real numbers to quantify data. Our next example explores a function defined using a table of numerical values.
Example 1.2.1
Example 1.2.1a
Suppose Skippy records the outdoor temperature every two hours starting at 6 a.m. and ending at 6 p.m. and summarizes the data in the table below:
![Rendered by QuickLaTeX.com \[\begin{array}{|c||c|} \hline \text{time (hours after 6 a.m.)} & \text{outdoor temperature} \\ & \text{in degrees Fahrenheit} \\ \hline 0 & 64 \\ \hline 2 & 67 \\ \hline 4 & 75 \\ \hline 6 & 80 \\ \hline 8 & 83 \\ \hline 10 & 83 \\ \hline 12 & 82 \\ \hline \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-854b262f05ffcbc275f694c3dbdae01d_l3.png)
Explain why the recorded outdoor temperature is a function of the corresponding time.
Solution:
Explain why the recorded outdoor temperature is a function of the corresponding time.
The outdoor temperature is a function of time because each time value is associated with only one recorded temperature.
Example 1.2.1b
Suppose Skippy records the outdoor temperature every two hours starting at 6 a.m. and ending at 6 p.m. and summarizes the data in the table below:
![Rendered by QuickLaTeX.com \[\begin{array}{|c||c|} \hline \text{time (hours after 6 a.m.)} & \text{outdoor temperature} \\ & \text{in degrees Fahrenheit} \\ \hline 0 & 64 \\ \hline 2 & 67 \\ \hline 4 & 75 \\ \hline 6 & 80 \\ \hline 8 & 83 \\ \hline 10 & 83 \\ \hline 12 & 82 \\ \hline \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-854b262f05ffcbc275f694c3dbdae01d_l3.png)
Is time a function of the outdoor temperature? Explain.
Solution:
Is time a function of the outdoor temperature? Explain.
Time is not a function of the outdoor temperature because there are instances when different times are associated with a given temperature. For example, the temperature ![]() corresponds to both of the times
corresponds to both of the times ![]() and
and ![]() .
.
Example 1.2.1.3a
Suppose Skippy records the outdoor temperature every two hours starting at 6 a.m. and ending at 6 p.m. and summarizes the data in the table below:
![Rendered by QuickLaTeX.com \[\begin{array}{|c||c|} \hline \text{time (hours after 6 a.m.)} & \text{outdoor temperature} \\ & \text{in degrees Fahrenheit} \\ \hline 0 & 64 \\ \hline 2 & 67 \\ \hline 4 & 75 \\ \hline 6 & 80 \\ \hline 8 & 83 \\ \hline 10 & 83 \\ \hline 12 & 82 \\ \hline \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-854b262f05ffcbc275f694c3dbdae01d_l3.png)
Let ![]() be the function which matches time to the corresponding recorded outdoor temperature. Compute and interpret the following:
be the function which matches time to the corresponding recorded outdoor temperature. Compute and interpret the following:
Solution:
Find and interpret: ![]() ,
, ![]() ,
, ![]() ,
, ![]() +
+ ![]() , and
, and ![]() .
.
- To find
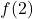 , we look in the table to find the recorded outdoor temperature that corresponds to when the time is
, we look in the table to find the recorded outdoor temperature that corresponds to when the time is 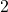 . We get
. We get 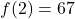 which means that 2 hours after 6 a.m. (i.e., at 8 a.m.), the temperature is
which means that 2 hours after 6 a.m. (i.e., at 8 a.m.), the temperature is 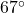 F.
F. - Per the table,
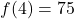 , so the recorded outdoor temperature at 10 a.m. (4 hours after 6 a.m.) is
, so the recorded outdoor temperature at 10 a.m. (4 hours after 6 a.m.) is 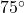 F.
F. - From the table, we find
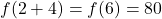 , which means that at noon (6 hours after 6 a.m.), the recorded outdoor temperature is
, which means that at noon (6 hours after 6 a.m.), the recorded outdoor temperature is 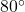 F.
F. - Using results from above we see that
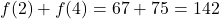 . When adding
. When adding 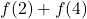 , we are adding the recorded outdoor temperatures at 8 a.m. (2 hours after 6 a.m.) and 10 a.m. (4 hours after 6 AM), respectively, to get
, we are adding the recorded outdoor temperatures at 8 a.m. (2 hours after 6 a.m.) and 10 a.m. (4 hours after 6 AM), respectively, to get 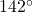 F.
F. - We compute
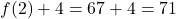 . Here, we are adding
. Here, we are adding 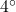 F to the outdoor temperature recorded at 8 a.m..
F to the outdoor temperature recorded at 8 a.m..
Example 1.2.1.3b
Suppose Skippy records the outdoor temperature every two hours starting at 6 a.m. and ending at 6 p.m. and summarizes the data in the table below:
![Rendered by QuickLaTeX.com \[\begin{array}{|c||c|} \hline \text{time (hours after 6 a.m.)} & \text{outdoor temperature} \\ & \text{in degrees Fahrenheit} \\ \hline 0 & 64 \\ \hline 2 & 67 \\ \hline 4 & 75 \\ \hline 6 & 80 \\ \hline 8 & 83 \\ \hline 10 & 83 \\ \hline 12 & 82 \\ \hline \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-854b262f05ffcbc275f694c3dbdae01d_l3.png)
Let ![]() be the function which matches time to the corresponding recorded outdoor temperature. Solve and interpret
be the function which matches time to the corresponding recorded outdoor temperature. Solve and interpret ![]() .
.
Solution:
Solve and interpret ![]() .
.
Solving ![]() means finding all of the input (time) values
means finding all of the input (time) values ![]() which produce an output value of
which produce an output value of ![]() . From the data, we see that the temperature is
. From the data, we see that the temperature is ![]() when the time is
when the time is ![]() or
or ![]() , so the solution to
, so the solution to ![]() is
is ![]() or
or ![]() . This means the outdoor temperature is
. This means the outdoor temperature is ![]() F at 2 p.m. (8 hours after 6 a.m.) and at 4 p.m. (10 hours after 6 a.m.).
F at 2 p.m. (8 hours after 6 a.m.) and at 4 p.m. (10 hours after 6 a.m.).
Example 1.2.1.3c
Suppose Skippy records the outdoor temperature every two hours starting at 6 a.m. and ending at 6 p.m. and summarizes the data in the table below:
![Rendered by QuickLaTeX.com \[\begin{array}{|c||c|} \hline \text{time (hours after 6 a.m.)} & \text{outdoor temperature} \\ & \text{in degrees Fahrenheit} \\ \hline 0 & 64 \\ \hline 2 & 67 \\ \hline 4 & 75 \\ \hline 6 & 80 \\ \hline 8 & 83 \\ \hline 10 & 83 \\ \hline 12 & 82 \\ \hline \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-854b262f05ffcbc275f694c3dbdae01d_l3.png)
Let ![]() be the function which matches time to the corresponding recorded outdoor temperature. State the range of
be the function which matches time to the corresponding recorded outdoor temperature. State the range of ![]() . What is lowest recorded temperature of the day? The highest?
. What is lowest recorded temperature of the day? The highest?
Solution:
State the range of ![]() . What is lowest recorded temperature of the day? The highest?
. What is lowest recorded temperature of the day? The highest?
The range of ![]() is the set of all of the outputs from
is the set of all of the outputs from ![]() , or in this case, the outside recorded temperatures. Based on the data, we get
, or in this case, the outside recorded temperatures. Based on the data, we get ![]() . (Here again, we list elements of a set only once.) The lowest recorded temperature of the day is
. (Here again, we list elements of a set only once.) The lowest recorded temperature of the day is ![]() F and the highest recorded temperature of the day is
F and the highest recorded temperature of the day is ![]() F.
F.
A few remarks about the example above are in order. First, note that ![]() ,
, ![]() and
and ![]() all work out to be numerically different, and more importantly, all represent different things.[8] One of the common mistakes students make is to misinterpret expressions like these, so it’s important to pay close attention to the syntax here.
all work out to be numerically different, and more importantly, all represent different things.[8] One of the common mistakes students make is to misinterpret expressions like these, so it’s important to pay close attention to the syntax here.
Finally, given that the range in this example was a finite set of real numbers, we could identify the smallest and largest elements of it. Here, they correspond to the coolest and warmest temperatures of the day, respectively, but the meaning would change if the function related different quantities. In many applications involving functions, the end goal is to identify the minimum or maximum values of the outputs of those functions (called optimizing the function) so for that reason, we have the following definition.
Definition 1.5
Suppose ![]() is a function whose range is a set of real numbers containing
is a function whose range is a set of real numbers containing ![]() and
and ![]() .
.
- The value
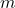 is called the absolute minimum[9] of
is called the absolute minimum[9] of  if
if 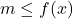 for all
for all  in the domain of
in the domain of  .
.
That is, the absolute minimum of is the smallest output from
is the smallest output from  , if it exists.
, if it exists. - The value
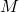 is called the absolute maximum[10] of
is called the absolute maximum[10] of  if
if 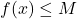 for all
for all  in the domain of
in the domain of  .
.
That is, the absolute maximum of is the largest output from
is the largest output from  , if it exists.
, if it exists. - Taken together, the values
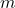 and
and 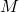 (if they exist) are called the absolute extrema[11] of
(if they exist) are called the absolute extrema[11] of  .
.
Definition 1.5 is an example where the name of the function, ![]() , is being used almost synonymously with its outputs in that when we speak of `the minimum and maximum of the function
, is being used almost synonymously with its outputs in that when we speak of `the minimum and maximum of the function ![]() ‘ we are really talking about the absolute minimum and absolute maximum values of the outputs
‘ we are really talking about the absolute minimum and absolute maximum values of the outputs ![]() as
as ![]() varies through the domain of
varies through the domain of ![]() . Thus, we say that the absolute maximum of
. Thus, we say that the absolute maximum of ![]() is
is ![]() and the absolute minimum of
and the absolute minimum of ![]() is
is ![]() when referring to the highest and lowest recorded temperatures in the previous example.
when referring to the highest and lowest recorded temperatures in the previous example.
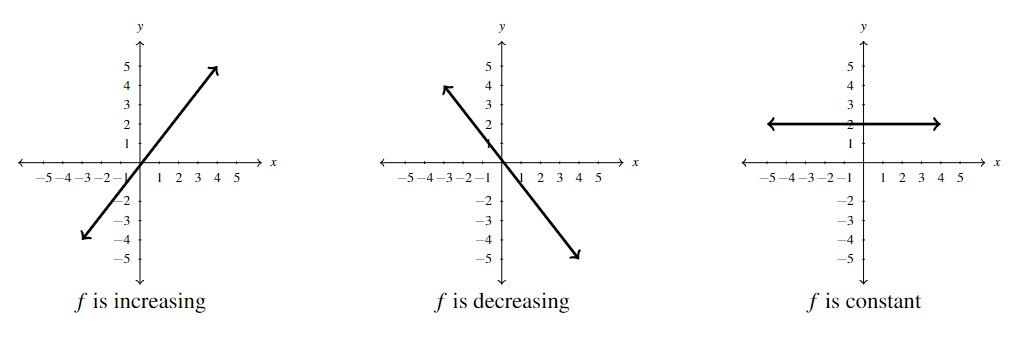
Definition 1.6
Let ![]() be a function defined on an interval
be a function defined on an interval ![]() . Then
. Then ![]() is said to be:
is said to be:
- increasing on
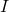 if, whenever
if, whenever 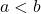 , then
, then 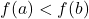 . (i.e., as inputs increase, outputs increase.)
. (i.e., as inputs increase, outputs increase.)
NOTE: The graph of an increasing function rises as one moves from left to right. - decreasing on
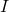 if, whenever
if, whenever 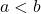 , then
, then 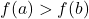 . (i.e., as inputs increase, outputs decrease.)
. (i.e., as inputs increase, outputs decrease.)
Note: The graph of a decreasing function falls as one moves from left to right. - constant on
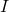 if
if 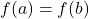 for all
for all  ,
,  in
in  . (i.e., outputs don’t change with inputs.)
. (i.e., outputs don’t change with inputs.)
NOTE: The graph of a function that is constant over an interval is a horizontal line.
Also, note that, like Definition 1.5, Definition 1.6 blurs the line between the function, ![]() , and its outputs,
, and its outputs, ![]() , because the verbiage `
, because the verbiage `![]() is increasing’ is really a statement about the outputs,
is increasing’ is really a statement about the outputs, ![]() . Finally, when we ask `where’ a function is increasing, decreasing or constant, we are looking for an interval of inputs. We’ll have more to say about this in later sections, but for now, we summarize these ideas graphically below.
. Finally, when we ask `where’ a function is increasing, decreasing or constant, we are looking for an interval of inputs. We’ll have more to say about this in later sections, but for now, we summarize these ideas graphically below.
 Another item of note about functions is the symmetry about the line
Another item of note about functions is the symmetry about the line ![]() (the
(the ![]() -axis). See Definition 1.1 for a review of this concept.) We have that for all
-axis). See Definition 1.1 for a review of this concept.) We have that for all ![]() ,
, ![]() on the graph of
on the graph of ![]() , the point symmetric about the
, the point symmetric about the ![]() -axis,
-axis, ![]() is on the graph, too. An investigation of symmetry with respect to the origin yields similar results with the major difference being that when a negative number is raised to an odd natural number power the result is still negative.
is on the graph, too. An investigation of symmetry with respect to the origin yields similar results with the major difference being that when a negative number is raised to an odd natural number power the result is still negative.
Definition 1.7
1.2.2 Algebraic Representations of Functions
By focusing our attention to functions that involve real numbers, we gain access to all of the structures and tools from prior courses in Algebra. In this subsection, we discuss how to represent functions algebraically using formulas and begin with the following example.
Example 1.2.2
Example 1.2.2.1a
Let ![]() be the function which takes a real number and performs the following sequence of operations:
be the function which takes a real number and performs the following sequence of operations:
- Step 1: add 2
- Step 2: multiply the result of Step 1 by 3
- Step 3: subtract 1 from the result of Step 2
Compute and simplify ![]() .
.
Solution:
Compute and simplify ![]() .
.
We take ![]() and follow it through each step:
and follow it through each step:
- Step 1: adding 2 gives us
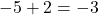 .
. - Step 2: multiplying the result of Step 1 by 3 yields
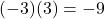 .
. - Step 3: subtracting 1 from the result of Step 2 produces
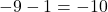 .
.
Hence, ![]() .
.
Example 1.2.2.1b
Let ![]() be the function which takes a real number and performs the following sequence of operations:
be the function which takes a real number and performs the following sequence of operations:
- Step 1: add 2
- Step 2: multiply the result of Step 1 by 3
- Step 3: subtract 1 from the result of Step 2
Identify and simplify a formula for ![]() .
.
Solution:
Identify and simplify a formula for ![]() .
.
To develop a formula for ![]() , we repeat the above process but use the variable `
, we repeat the above process but use the variable `![]() ‘ in place of the number
‘ in place of the number ![]() :
:
- Step 1: adding 2 gives us the quantity
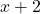 .
. - Step 2: multiplying the result of Step 1 by 3 yields
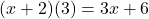 .
. - Step 3: subtracting 1 from the result of Step 2 produces
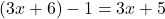 .
.
Hence, we have codified ![]() using the formula
using the formula ![]() . In other words, the function
. In other words, the function ![]() matches each real number `
matches each real number `![]() ‘ with the value of the expression `
‘ with the value of the expression `![]() ‘. As a partial check of our answer, we use this formula to find
‘. As a partial check of our answer, we use this formula to find ![]() . We compute
. We compute ![]() by substituting
by substituting ![]() into the formula
into the formula ![]() and find
and find ![]() as before.
as before.
Example 1.2.2.2ai
Let ![]() . Compute and simplify the following:
. Compute and simplify the following:
![]() ,
, ![]() and
and ![]()
Solution:
Given ![]() , compute and simplify
, compute and simplify ![]() ,
, ![]() and
and ![]() .
.
As before, representing the function ![]() as
as ![]() means that
means that ![]() matches the real number
matches the real number ![]() with the value of the expression
with the value of the expression ![]() .
.
To find ![]() , we substitute
, we substitute ![]() for
for ![]() in the expression
in the expression ![]() . It is highly recommended that you be generous with parentheses here in order to avoid common mistakes:
. It is highly recommended that you be generous with parentheses here in order to avoid common mistakes:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} h(-1) & = & -(-1)^2 + 3(-1) + 4 & \\ [2pt] & = & -(1) + (-3) + 4 & \\ [2pt] & = & 0 .& \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f7e0e2c62f4f8bfce54de937112bb800_l3.png)
Similarly,
![]()
and
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} h(2) &=& -(2)^2 + 3(2) + 4 \\ &=& -4 + 6 + 4 \\ &=& 6 \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a190c202676fcb3c3f5a24a7edbb0757_l3.png)
Example 1.2.2.2aii
Let ![]() . Compute and simplify the following:
. Compute and simplify the following:
![]() and
and ![]()
Solution:
Given ![]() , compute and simplify
, compute and simplify ![]() and
and ![]() .
.
To find ![]() , we substitute
, we substitute ![]() for
for ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} h(2x) & = & -(2x)^2 + 3(2x) + 4 & \\ [2pt] & = & -(4x^2) + (6x) + 4 & \\ [2pt] & = & -4x^2+6x+4. & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c97beee9e5430d0bdd11e5416181af1f_l3.png)
The expression ![]() means that we multiply the expression
means that we multiply the expression ![]() by
by ![]() . We first get
. We first get ![]() by substituting
by substituting ![]() for
for ![]() :
: ![]() . Hence,
. Hence,
![]()
Example 1.2.2.2aiii
Let ![]() . Compute and simplify the following:
. Compute and simplify the following:
![]() ,
, ![]() and
and ![]()
Solution:
Given ![]() , compute and simplify
, compute and simplify ![]() ,
, ![]() and
and ![]() .
.
To find ![]() , we substitute the quantity
, we substitute the quantity ![]() in place of
in place of ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} h(t + 2) & = & -(t + 2)^2 + 3(t + 2) + 4 & \\ [2pt] & = & -\left(t\,^{2} + 4t + 4\right) + (3t + 6) + 4 & \\ [2pt] & = & -t\,^{2} - 4t - 4 + 3t + 6 + 4 & \\ [2pt] & = & -t\,^{2} - t + 6. & \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-22fb0083b6dcfd93610b7ca7dcf3180c_l3.png)
To find ![]() , we add
, we add ![]() to the expression for
to the expression for ![]()
![]()
From our work above, we see that ![]() so
so
![]()
Example 1.2.2.2b
Let ![]() . Solve
. Solve ![]() .
.
Solution:
Solve ![]() .
.
We know ![]() from above, so
from above, so ![]() should be one of the answers to
should be one of the answers to ![]() . In order to see if there are any more, we set
. In order to see if there are any more, we set ![]() . Factoring[12] gives
. Factoring[12] gives ![]() , so we get
, so we get ![]() (as expected) along with
(as expected) along with ![]() .
.
A few remarks about Example 1.2.2 are in order. First, note that ![]() and
and ![]() are different expressions. In the former, we are multiplying the input by
are different expressions. In the former, we are multiplying the input by ![]() ; in the latter, we are multiplying the output by
; in the latter, we are multiplying the output by ![]() . The same goes for
. The same goes for ![]() ,
, ![]() and
and ![]() . The expression
. The expression ![]() calls for adding
calls for adding ![]() to the input
to the input ![]() and then performing the function
and then performing the function ![]() . The expression
. The expression ![]() has us performing the process
has us performing the process ![]() first, then adding
first, then adding ![]() to the output
to the output ![]() . Finally,
. Finally, ![]() directs us to first find the outputs
directs us to first find the outputs ![]() and
and ![]() and then add the results. As we saw in Example 1.2.1, we see here again the importance paying close attention to syntax.[13]
and then add the results. As we saw in Example 1.2.1, we see here again the importance paying close attention to syntax.[13]
Let us return for a moment to the function ![]() in Example 1.2.2 which we ultimately represented using the formula
in Example 1.2.2 which we ultimately represented using the formula ![]() . If we introduce the dependent variable
. If we introduce the dependent variable ![]() , we get the equation
, we get the equation ![]() , or, more simply
, or, more simply ![]() . To say that the equation
. To say that the equation ![]() describes
describes ![]() as a function of
as a function of ![]() means that for each choice of
means that for each choice of ![]() , the formula
, the formula ![]() determines only one associated
determines only one associated ![]() -value.
-value.
We could turn the tables and ask if the equation ![]() describes
describes ![]() as a function of
as a function of ![]() . That is, for each value we pick for
. That is, for each value we pick for ![]() , does the equation
, does the equation ![]() produce only one associated
produce only one associated ![]() value? One way to proceed is to solve
value? One way to proceed is to solve ![]() for
for ![]() and get
and get ![]() . We see that for each choice of
. We see that for each choice of ![]() , the expression
, the expression ![]() evaluates to just one number, hence,
evaluates to just one number, hence, ![]() is a function of
is a function of ![]() . If we give this function a name, say
. If we give this function a name, say ![]() , we have
, we have ![]() , where in this equation,
, where in this equation, ![]() is the independent variable and
is the independent variable and ![]() is the dependent variable. We explore this idea in the next example.
is the dependent variable. We explore this idea in the next example.
Example 1.2.3
Example 1.2.3.1a
Consider the equation ![]() . Does this equation represent
. Does this equation represent ![]() as a function of
as a function of ![]() ? Explain.
? Explain.
Solution:
Does ![]() represent
represent ![]() as a function of
as a function of ![]() ? Explain.
? Explain.
To say that ![]() represents
represents ![]() as a function of
as a function of ![]() , we need to show that for each
, we need to show that for each ![]() we choose, the equation produces only one associated
we choose, the equation produces only one associated ![]() -value. To help with this analysis, we solve the equation for
-value. To help with this analysis, we solve the equation for ![]() in terms of
in terms of ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} x^{3} + y^{2} & = & 25 & \\ y^{2} & = & 25 - x^{3} & \\ y & = & \pm \sqrt{25 - x^{3}} & \text{extract square roots. (See Section 0.5 for a review, if needed.)} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f3fbbaf0a2bbce9ff388dd3227b555c4_l3.png)
The presence of the `![]() ‘ indicates that there is a good chance that for some
‘ indicates that there is a good chance that for some ![]() -value, the equation will produce two corresponding
-value, the equation will produce two corresponding ![]() -values. Indeed,
-values. Indeed, ![]() produces
produces ![]() .
.
Hence, ![]() equation does not represent
equation does not represent ![]() as a function of
as a function of ![]() because
because ![]() is matched with more than one
is matched with more than one ![]() -value.
-value.
Example 1.2.3.1b
Consider the equation ![]() . Does this equation represent
. Does this equation represent ![]() as a function of
as a function of ![]() ? Explain.
? Explain.
Solution:
Does ![]() represent
represent ![]() as a function of
as a function of ![]() ? Explain.
? Explain.
To see if ![]() represents
represents ![]() as a function of
as a function of ![]() , we solve the equation for
, we solve the equation for ![]() in terms of
in terms of ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} x^{3} + y^{2} & = & 25 & \\ x^{3} & = & 25 - y^{2}& \\ & = & \sqrt[3]{25 - y^{2}} & \text{extract cube roots. (See Section 0.2 for a review, if needed.)} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-16da709e9bc9db21bd192b7240e238c1_l3.png)
In this case, each choice of ![]() produces only one corresponding value for
produces only one corresponding value for ![]() , so
, so ![]() represents
represents ![]() as a function of
as a function of ![]() .
.
Example 1.2.3.2a
Consider the equation ![]() . Does this equation represent
. Does this equation represent ![]() as a function of
as a function of ![]() ? Explain.
? Explain.
Solution:
Does ![]() represent
represent ![]() as a function of
as a function of ![]() ? Explain.
? Explain.
To see if ![]() represents
represents ![]() as a function of
as a function of ![]() , we proceed as above and solve for
, we proceed as above and solve for ![]() in terms of
in terms of ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} u^{4} + t^{3} u & = & 16 & \\ t^{3} u & = & 16 - u^{4} & \\ [6pt] t^{3} & = & \dfrac{16 - u^{4}}{u} & \text{assumes $u \neq 0$} \\ [10pt] t & = & \sqrt[3]{\dfrac{16 - u^{4}}{u}} & \text{extract cube roots.} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-86e605188815a0b086bd2b11bdd27efd_l3.png)
Although it’s a bit cumbersome, as long as ![]() the expression
the expression ![]() will produce just one value of
will produce just one value of ![]() for each value of
for each value of ![]() . What if
. What if ![]() ? In that case, the equation
? In that case, the equation ![]() reduces to
reduces to ![]() – which is never true – so we don’t need to worry about that case.[14]
– which is never true – so we don’t need to worry about that case.[14]
Hence, ![]() represents
represents ![]() as a function of
as a function of ![]() .
.
Example 1.2.3.2b
Consider the equation ![]() . Does this equation represent
. Does this equation represent ![]() as a function of
as a function of ![]() ? Explain.
? Explain.
Solution:
Does ![]() represent
represent ![]() as a function of
as a function of ![]() ? Explain.
? Explain.
In order to determine if ![]() represents
represents ![]() as a function of
as a function of ![]() , we could attempt to solve
, we could attempt to solve ![]() for
for ![]() in terms of
in terms of ![]() , but we won’t get very far.[15] Instead, we take a different approach and experiment with looking for solutions for
, but we won’t get very far.[15] Instead, we take a different approach and experiment with looking for solutions for ![]() for specific values of
for specific values of ![]() . If we let
. If we let ![]() , we get
, we get ![]() which gives
which gives ![]() .
.
Hence, ![]() corresponds to more than one
corresponds to more than one ![]() -value which means
-value which means ![]() does not represent
does not represent ![]() as a function of
as a function of ![]() .
.
We’ll have more to say about using equations to describe functions later in this section. For now, we turn our attention to a geometric way to represent functions.
1.2.3 Geometric Representations of Functions
In this subsection, we introduce how to graph functions. As we’ll see in this and later sections, visualizing functions geometrically can assist us in both analyzing them and using them to solve associated application problems. Our playground, if you will, for the Geometry in this course is the Cartesian Coordinate Plane. The reader would do well to review Section 1.1 as needed.
Our path to the Cartesian Plane requires ordered pairs. In general, we can represent every function as a set of ordered pairs. Indeed, given a function ![]() with domain
with domain ![]() , we can represent
, we can represent ![]() . That is, we represent
. That is, we represent ![]() as a set of ordered pairs
as a set of ordered pairs ![]() , or, more generally,
, or, more generally, ![]() . For example, the function
. For example, the function ![]() which matches Taylor’s pet’s names to their associated pet type can be represented as:
which matches Taylor’s pet’s names to their associated pet type can be represented as:
![]()
Moving on, we next consider the function ![]() from Example 1.2.1 which relates time to temperature. In this case,
from Example 1.2.1 which relates time to temperature. In this case, ![]() . This function has numerical values for both the domain and range so we can identify these ordered pairs with points in the Cartesian Plane. The first coordinates of these points (the abscissae) represent time values so we’ll use
. This function has numerical values for both the domain and range so we can identify these ordered pairs with points in the Cartesian Plane. The first coordinates of these points (the abscissae) represent time values so we’ll use ![]() to label the horizontal axis. Likewise, we’ll use
to label the horizontal axis. Likewise, we’ll use ![]() to label the vertical axis because the second coordinates of these points (the ordinates) represent temperature values. Note that labeling these axes in this way determines our independent and dependent variable names,
to label the vertical axis because the second coordinates of these points (the ordinates) represent temperature values. Note that labeling these axes in this way determines our independent and dependent variable names, ![]() and
and ![]() , respectively.
, respectively.
The plot of these points is called `the graph of ![]() ‘. More specifically, we could describe this plot as `the graph of
‘. More specifically, we could describe this plot as `the graph of ![]() ‘, because we have decided to name the independent variable
‘, because we have decided to name the independent variable ![]() . Most specifically, we could describe the plot as `the graph of
. Most specifically, we could describe the plot as `the graph of ![]() ‘, given that we have named the independent variable
‘, given that we have named the independent variable ![]() and the dependent variable
and the dependent variable ![]() .
.
Below we present two plots, both of which are graphs of the function ![]() . In both cases, the vertical axis has been scaled in order to save space. In the graph on the left, the same increment on the horizontal axis to measure
. In both cases, the vertical axis has been scaled in order to save space. In the graph on the left, the same increment on the horizontal axis to measure ![]() unit measures
unit measures ![]() units on the vertical axis whereas in the graph on the right, this ratio is
units on the vertical axis whereas in the graph on the right, this ratio is ![]() . The `
. The `![]() ‘ symbol on the vertical axis in the graph on the right is used to indicate a jump in the vertical labeling. Both are perfectly accurate data plots, but they have different visual impacts. Note here that the extrema of
‘ symbol on the vertical axis in the graph on the right is used to indicate a jump in the vertical labeling. Both are perfectly accurate data plots, but they have different visual impacts. Note here that the extrema of ![]() ,
, ![]() and
and ![]() , correspond to the lowest and highest points on the graph, respectively:
, correspond to the lowest and highest points on the graph, respectively: ![]() ,
, ![]() and
and ![]() . More often than not, we will use the graph of a function to help us optimize that function.[16]
. More often than not, we will use the graph of a function to help us optimize that function.[16]
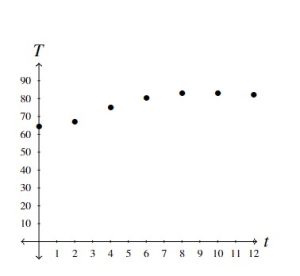
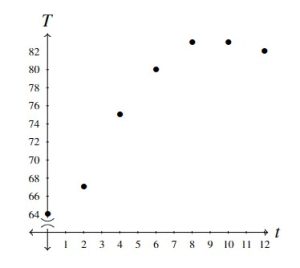
If you found yourself wanting to connect the dots in the graphs above, you’re not alone. As it stands, however, the function ![]() matches only seven inputs to seven outputs, so those seven points – and just those seven points – comprise the graph of
matches only seven inputs to seven outputs, so those seven points – and just those seven points – comprise the graph of ![]() . That being said, common everyday experience tells us that while the data Skippy collected in his table gives some good information about the relationship between time and temperature on a given day, it is by no means a complete description of the relationship.
. That being said, common everyday experience tells us that while the data Skippy collected in his table gives some good information about the relationship between time and temperature on a given day, it is by no means a complete description of the relationship.
Skippy’s temperature function ![]() is an example of a discrete function in the sense that each of the data points are `isolated’ with measurable gaps in between. The idea of `filling in’ those gaps is a quest to find a continuous function to model this same phenomenon.[17] We’ll return to this example in Sections 1.3.1 and 2.1 in an attempt to do just that.
is an example of a discrete function in the sense that each of the data points are `isolated’ with measurable gaps in between. The idea of `filling in’ those gaps is a quest to find a continuous function to model this same phenomenon.[17] We’ll return to this example in Sections 1.3.1 and 2.1 in an attempt to do just that.
In the meantime, our next example involves a function whose domain is (almost) an interval of real numbers and whose graph consists of a (mostly) connected arc.
Example 1.2.4
Example 1.2.4.1a
Consider the graph below.

Explain why this graph suggests that ![]() is a function of
is a function of ![]() ,
, ![]() .
.
Solution:
The challenge in working with only a graph is that unless points are specifically labeled (as some are in this case), we are forced to approximate values. In addition to the labeled points, there are other interesting features of the graph; a gap or `hole’ labeled ![]() and an arrow on the upper right hand part of the curve. We’ll have more to say about these two features shortly.
and an arrow on the upper right hand part of the curve. We’ll have more to say about these two features shortly.

Explain why this graph suggests that ![]() is a function of
is a function of ![]() ,
, ![]() .
.
In order for ![]() to be a function of
to be a function of ![]() , each
, each ![]() -value on the graph must be paired with only one
-value on the graph must be paired with only one ![]() -value. What if this weren’t the case? We’d have at least two points with the same
-value. What if this weren’t the case? We’d have at least two points with the same ![]() -coordinate with different
-coordinate with different ![]() -coordinates. Graphically, we’d have two points on graph on the same vertical line, one above the other. This never happens so we may conclude that
-coordinates. Graphically, we’d have two points on graph on the same vertical line, one above the other. This never happens so we may conclude that ![]() is a function of
is a function of ![]() .
.
Example 1.2.4.1b
Consider the graph below.

Compute ![]() and solve
and solve ![]() .
.
Solution:
The challenge in working with only a graph is that unless points are specifically labeled (as some are in this case), we are forced to approximate values. In addition to the labeled points, there are other interesting features of the graph; a gap or `hole’ labeled ![]() and an arrow on the upper right hand part of the curve. We’ll have more to say about these two features shortly.
and an arrow on the upper right hand part of the curve. We’ll have more to say about these two features shortly.

Compute ![]() and solve
and solve ![]() .
.
The value ![]() is the output from
is the output from ![]() when
when ![]() . The points on the graph of
. The points on the graph of ![]() are of the form
are of the form ![]() , thus we are looking for the
, thus we are looking for the ![]() -coordinate of the point on the graph where
-coordinate of the point on the graph where ![]() . Given that the point
. Given that the point ![]() is labeled on the graph (see below), we can be sure
is labeled on the graph (see below), we can be sure ![]() .
.

To solve ![]() , we are looking for the
, we are looking for the ![]() -values where the output, or associated
-values where the output, or associated ![]() value, is
value, is ![]() . Hence, we are looking for points on the graph with a
. Hence, we are looking for points on the graph with a ![]() -coordinate of
-coordinate of ![]() . We identify two such points,
. We identify two such points, ![]() and
and ![]() , so our solutions to
, so our solutions to ![]() are
are ![]() .
.

Example 1.2.4.1c
Consider the graph below.

State the domain and range of ![]() using interval notation.[18] Then identify the extrema of
using interval notation.[18] Then identify the extrema of ![]() , if any exist.
, if any exist.
Solution:
The challenge in working with only a graph is that unless points are specifically labeled (as some are in this case), we are forced to approximate values. In addition to the labeled points, there are other interesting features of the graph; a gap or `hole’ labeled ![]() and an arrow on the upper right hand part of the curve. We’ll have more to say about these two features shortly.
and an arrow on the upper right hand part of the curve. We’ll have more to say about these two features shortly.

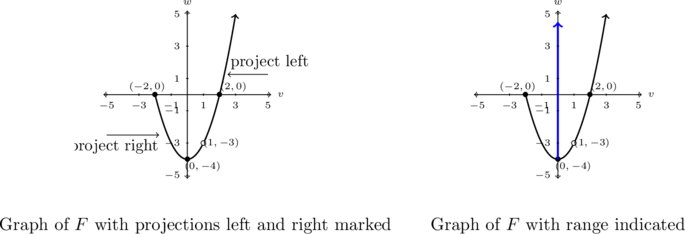
State the domain and range of ![]() using interval notation. Identify the extrema of
using interval notation. Identify the extrema of ![]() , if any exist.
, if any exist.
The domain of ![]() is the set of inputs to
is the set of inputs to ![]() . With
. With ![]() as the input here, we need to describe the set of
as the input here, we need to describe the set of ![]() -values on the graph. We can accomplish this by projecting the graph to the
-values on the graph. We can accomplish this by projecting the graph to the ![]() -axis and seeing what part of the
-axis and seeing what part of the ![]() -axis is covered. The leftmost point on the graph is
-axis is covered. The leftmost point on the graph is ![]() , so we know that the domain starts at
, so we know that the domain starts at ![]() . The graph continues to the right until we encounter the `hole’ labeled at
. The graph continues to the right until we encounter the `hole’ labeled at ![]() . This indicates one and only one point, namely
. This indicates one and only one point, namely ![]() is missing from the curve which for us means
is missing from the curve which for us means ![]() is not in the domain of
is not in the domain of ![]() . The graph continues to the right and the arrow on the graph indicates that the graph goes upwards to the right indefinitely.
. The graph continues to the right and the arrow on the graph indicates that the graph goes upwards to the right indefinitely.
Hence, our domain is ![]() which, in interval notation, is
which, in interval notation, is ![]() .
.
Pictures demonstrating the process of projecting the graph to the ![]() -axis are shown below.
-axis are shown below.

To find the range of ![]() , we need to describe the set of outputs – in this case, the
, we need to describe the set of outputs – in this case, the ![]() -values on the graph. Here, we project the graph to the
-values on the graph. Here, we project the graph to the ![]() -axis. Vertically, the graph starts at
-axis. Vertically, the graph starts at ![]() so our range starts at
so our range starts at ![]() . Note that even though there is a hole at
. Note that even though there is a hole at ![]() , the
, the ![]() -value
-value ![]() is covered by what appears to be the point
is covered by what appears to be the point ![]() on the graph.[19]
on the graph.[19]
The arrow indicates that the graph extends upwards indefinitely so the range of ![]() is
is ![]() or, in interval notation,
or, in interval notation, ![]() . Regarding extrema,
. Regarding extrema, ![]() has a minimum of
has a minimum of ![]() when
when ![]() , but given that the graph extends upwards indefinitely,
, but given that the graph extends upwards indefinitely, ![]() has no maximum.
has no maximum.
Pictures showing the projection of the graph onto the ![]() -axis are given below.
-axis are given below.
Example 1.2.4.2
Consider the graph below.

Does this graph suggest ![]() is a function of
is a function of ![]() ? Explain.
? Explain.
Solution:
The challenge in working with only a graph is that unless points are specifically labeled (as some are in this case), we are forced to approximate values. In addition to the labeled points, there are other interesting features of the graph; a gap or `hole’ labeled ![]() and an arrow on the upper right hand part of the curve. We’ll have more to say about these two features shortly.
and an arrow on the upper right hand part of the curve. We’ll have more to say about these two features shortly.

Does this graph suggest ![]() is a function of
is a function of ![]() ? Explain.
? Explain.
Finally, to determine if ![]() is a function of
is a function of ![]() , we look to see if each
, we look to see if each ![]() -value is paired with only one
-value is paired with only one ![]() -value on the graph. We have points on the graph, namely
-value on the graph. We have points on the graph, namely ![]() and
and ![]() , that clearly show us that
, that clearly show us that ![]() is matched with the two
is matched with the two ![]() -values
-values ![]() and
and ![]() .
.
Hence, ![]() is not a function of
is not a function of ![]() .
.
It cannot be stressed enough that when given a graphical representation of a function, certain assumptions must be made. In the previous example, for all we know, the minimum of the graph is at ![]() instead of
instead of ![]() . If we aren’t given an equation or table of data, or if specific points aren’t labeled, we really have no way to tell. We also are assuming that the graph depicted in the example, while ultimately made of infinitely many points, has no gaps or holes other than those noted. This allows us to make such bold claims as the existence of a point on the graph with a
. If we aren’t given an equation or table of data, or if specific points aren’t labeled, we really have no way to tell. We also are assuming that the graph depicted in the example, while ultimately made of infinitely many points, has no gaps or holes other than those noted. This allows us to make such bold claims as the existence of a point on the graph with a ![]() -coordinate of
-coordinate of ![]() .
.
Before moving on to our next example, it is worth noting that the geometric argument made in Example 1.2.4 to establish that ![]() is a function of
is a function of ![]() can be generalized to any graph. This result is the celebrated Vertical Line Test and it enables us to detect functions geometrically. Note that the statement of the theorem resorts to the `default’
can be generalized to any graph. This result is the celebrated Vertical Line Test and it enables us to detect functions geometrically. Note that the statement of the theorem resorts to the `default’ ![]() and
and ![]() labels on the horizontal and vertical axes, respectively.
labels on the horizontal and vertical axes, respectively.
Theorem 1.2 The Vertical Line Test
A graph in the ![]() -plane[20] represents
-plane[20] represents ![]() as a function of
as a function of ![]() if and only if no vertical line intersects the graph more than once.
if and only if no vertical line intersects the graph more than once.
Let’s take a minute to discuss the phrase `if and only if’ used in Theorem 1.2. The statement `the graph represents ![]() as a function of
as a function of ![]() if and only if no vertical line intersects the graph more than once’ is actually saying two things. First, it’s saying `the graph represents
if and only if no vertical line intersects the graph more than once’ is actually saying two things. First, it’s saying `the graph represents ![]() as a function of
as a function of ![]() if no vertical line intersects the graph more than once’ and, second, `the graph represents
if no vertical line intersects the graph more than once’ and, second, `the graph represents ![]() as a function of
as a function of ![]() only if no vertical line intersects the graph more than once’.
only if no vertical line intersects the graph more than once’.
Logically, these statements are saying two different things. The first says that if no vertical line crosses the graph more than once, then the graph represents ![]() as a function of
as a function of ![]() . But the question remains: could a graph represent
. But the question remains: could a graph represent ![]() as a function of
as a function of ![]() and yet there be a vertical line that intersects the graph more than once? The answer to this is `no’ because the second statement says that the only way the graph represents
and yet there be a vertical line that intersects the graph more than once? The answer to this is `no’ because the second statement says that the only way the graph represents ![]() as a function of
as a function of ![]() is the case when no vertical line intersects the graph more than once.
is the case when no vertical line intersects the graph more than once.
Applying the Vertical Line Test to the graph given in Example 1.2.4, we see below that all of the vertical lines meet the graph at most once (several are shown for illustration) showing ![]() is a function of
is a function of ![]() . Notice that some of the lines (
. Notice that some of the lines (![]() and
and ![]() , for example) don’t hit the graph at all. This is fine because the Vertical Line Test is looking for lines that hit the graph more than once. It does not say exactly once so missing the graph altogether is permitted.
, for example) don’t hit the graph at all. This is fine because the Vertical Line Test is looking for lines that hit the graph more than once. It does not say exactly once so missing the graph altogether is permitted.
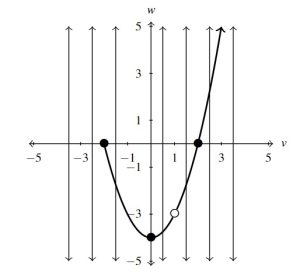
There is also a geometric test to determine if the graph above represents ![]() as a function of
as a function of ![]() . We introduce this aptly-named Horizontal Line Test in Exercise 57 and revisit it in Sections 5.1.
. We introduce this aptly-named Horizontal Line Test in Exercise 57 and revisit it in Sections 5.1.
Our next example revisits the function ![]() from Example 1.2.2 from a graphical perspective.
from Example 1.2.2 from a graphical perspective.
Example 1.2.5
Example 1.2.5
Using the graph of ![]() below, state the domain, range, any absolute extrema, and the intervals where
below, state the domain, range, any absolute extrema, and the intervals where ![]() is increasing, decreasing, or constant, if any exist.
is increasing, decreasing, or constant, if any exist.
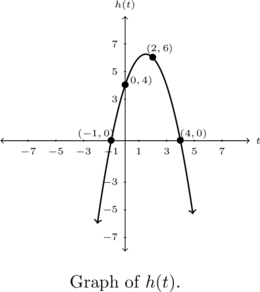
Solution:
The dependent variable wasn’t specified so we use the default `![]() ‘ label for the vertical axis and set about graphing
‘ label for the vertical axis and set about graphing ![]() . From our work in Example 1.2.2, we already know
. From our work in Example 1.2.2, we already know ![]() ,
, ![]() ,
, ![]() and
and ![]() . These give us the points
. These give us the points ![]() ,
, ![]() ,
, ![]() and
and ![]() , respectively.
, respectively.
Using these as a guide, we produce the graph above.[21]
As nice as the graph is, it is still technically incomplete. There is no restriction stated on the independent variable ![]() so the domain of
so the domain of ![]() is all real numbers. However, the graph as presented shows only the behavior of
is all real numbers. However, the graph as presented shows only the behavior of ![]() between roughly
between roughly ![]() and
and ![]() . The arrows at the ends of our graph indicate the graph extends downwards indefinitely.
. The arrows at the ends of our graph indicate the graph extends downwards indefinitely.
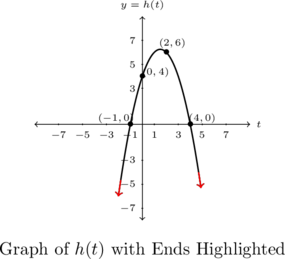
Using projections below, we note that the domain is ![]() and the range is
and the range is ![]() .
.
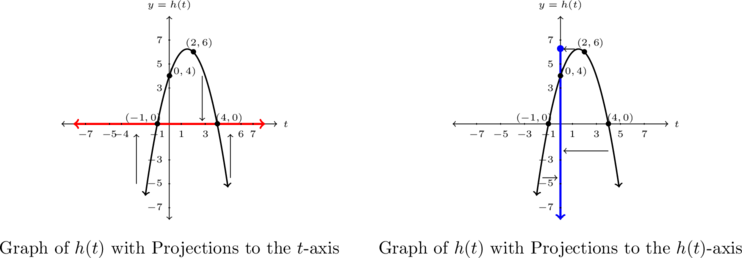
There is no minimum, but the maximum of ![]() is
is ![]() and it occurs at
and it occurs at ![]() . The point
. The point ![]() is shown on the graph.
is shown on the graph.

![]() is increasing on the interval
is increasing on the interval ![]() and
and ![]() is decreasing on the interval
is decreasing on the interval ![]() .
. ![]() is not constant on any interval.
is not constant on any interval.

Our last example of the section uses the interplay between algebraic and graphical representations of a function to solve a real-world problem.
Example 1.2.6
Example 1.2.6a
The United States Postal Service mandates that when shipping parcels using `Parcel Select’ service, the sum of the length (the longest dimension) and the girth (the distance around the thickest part of the parcel perpendicular to the length) must not exceed 130 inches.[22] Suppose we wish to ship a rectangular box whose girth forms a square measuring ![]() inches per side as shown below.
inches per side as shown below.
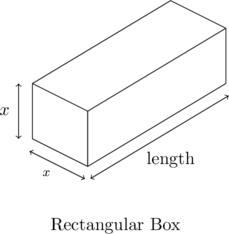
It turns out[23] that the volume of a box, ![]() , measured in cubic inches, whose length plus girth is exactly 130 inches is given by the formula:
, measured in cubic inches, whose length plus girth is exactly 130 inches is given by the formula: ![]() for
for ![]() .
.
Compute and interpret ![]() .
.
Solution:
Compute and interpret ![]() .
.
To compute ![]() , we substitute
, we substitute ![]() into the expression
into the expression ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} V(5) &=& (5)^2 (130-4(5)) \\ &=& 25(110)\\ &=& 2750. \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-34a9ca51dda96aac1a2015be69c87353_l3.png)
Our result means that when the length and width of the square measure ![]() inches, the volume of the resulting box is
inches, the volume of the resulting box is ![]() cubic inches.[24]
cubic inches.[24]
Example 1.2.6b
The United States Postal Service mandates that when shipping parcels using `Parcel Select’ service, the sum of the length (the longest dimension) and the girth (the distance around the thickest part of the parcel perpendicular to the length) must not exceed 130 inches. Suppose we wish to ship a rectangular box whose girth forms a square measuring ![]() inches per side as shown below.
inches per side as shown below.

It turns out that the volume of a box, ![]() , measured in cubic inches, whose length plus girth is exactly 130 inches is given by the formula:
, measured in cubic inches, whose length plus girth is exactly 130 inches is given by the formula: ![]() for
for ![]() .
.
Make a table of values and use these to sketch a graph ![]() .
.
Solution:
Make a table of values and use these to sketch a graph ![]() .
.
The domain of ![]() is specified by the inequality
is specified by the inequality ![]() , so we can begin graphing
, so we can begin graphing ![]() by sampling
by sampling ![]() at finitely many
at finitely many ![]() -values in this interval to help us get a sense of the range of
-values in this interval to help us get a sense of the range of ![]() . This, in turn, will help us determine an adequate viewing window on our graphing utility when the time comes.
. This, in turn, will help us determine an adequate viewing window on our graphing utility when the time comes.
It seems natural to start with what’s happening near ![]() . Even though the expression
. Even though the expression ![]() is defined when we substitute
is defined when we substitute ![]() (it reduces very quickly to
(it reduces very quickly to ![]() ), it would be incorrect to state
), it would be incorrect to state ![]() because
because ![]() is not in the domain of
is not in the domain of ![]() . However, there is nothing stopping us from evaluating
. However, there is nothing stopping us from evaluating ![]() at values
at values ![]() `very close’ to
`very close’ to ![]() . A table of such values is given below.
. A table of such values is given below.
![Rendered by QuickLaTeX.com \[ \begin{array}{||l|l||} \hline x & V(x) \\ \hline 0.1 & 1.296 \\ \hline 0.01 & 0.012996 \\ \hline 0.001 & 0.000129996 \\ \hline 10^{-23} & \approx 1.3 \times 10^{-44} \\ \hline \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5ee3a6e74cf4462f01d6b16da2d7537f_l3.png)
There is no such thing as a `smallest’ positive number,[25] so we will have points on the graph of ![]() to the right of
to the right of ![]() leading to the point
leading to the point ![]() . We indicate this behavior by putting a hole at
. We indicate this behavior by putting a hole at ![]() .[26]
.[26]
Moving forward, we start with ![]() and sample
and sample ![]() at steps of
at steps of ![]() in its domain. Our goal is to graph
in its domain. Our goal is to graph ![]() , so we plot our points
, so we plot our points ![]() using the domain as a guide to help us set the horizontal bounds (i.e., the bounds on
using the domain as a guide to help us set the horizontal bounds (i.e., the bounds on ![]() ) and the sample values from the range to help us set the vertical bounds (i.e., the bounds on
) and the sample values from the range to help us set the vertical bounds (i.e., the bounds on ![]() ).
).
![Rendered by QuickLaTeX.com \[\begin{array}{|r||c|c|} \hline x & V(x) & (x,V(x)) \\ \hline \approx 0 & \approx 0 & \text{hole at $(0,0)$} \\ \hline 5 & 2750 & (5, 2750) \\ \hline 10 & 9000 & (10, 9000) \\ \hline 15 & 15, \! 750 & ( 15, 15750) \\ \hline 20 & 20, \! 000 & ( 20 , 20000) \\ \hline 25 & 18, \! 750 & ( 25, 18750) \\ \hline 26 & 17, \! 576 & (26,17576) \\ \hline \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a0eb512b307d2353431d4583607f3396_l3.png)
The right endpoint, ![]() , is included in the domain
, is included in the domain ![]() so we finish the graph by plotting the point
so we finish the graph by plotting the point ![]() .
.

Example 1.2.6c
The United States Postal Service mandates that when shipping parcels using `Parcel Select’ service, the sum of the length (the longest dimension) and the girth (the distance around the thickest part of the parcel perpendicular to the length) must not exceed 130 inches. Suppose we wish to ship a rectangular box whose girth forms a square measuring ![]() inches per side as shown below.
inches per side as shown below.

It turns out that the volume of a box, ![]() , measured in cubic inches, whose length plus girth is exactly 130 inches is given by the formula:
, measured in cubic inches, whose length plus girth is exactly 130 inches is given by the formula: ![]() for
for ![]() .
.
What is the largest volume box that can be shipped? What value of ![]() maximizes the volume? Round your answers to two decimal places.
maximizes the volume? Round your answers to two decimal places.
Solution:
What is the largest volume box that can be shipped? What value of ![]() maximizes the volume? Round your answers to two decimal places.
maximizes the volume? Round your answers to two decimal places.
The largest volume in this case refers to the maximum of ![]() . The biggest
. The biggest ![]() -value in our table of data is
-value in our table of data is ![]() cubic inches which occurs at
cubic inches which occurs at ![]() inches, but the graph produced by the graphing utility indicates that there are points on the graph of
inches, but the graph produced by the graphing utility indicates that there are points on the graph of ![]() with
with ![]() -values (hence
-values (hence ![]() values) greater than
values) greater than ![]() . Indeed, the graph continues to rise to the right of
. Indeed, the graph continues to rise to the right of ![]() and with the use of technology we can determine the maximum
and with the use of technology we can determine the maximum ![]() -value to be
-value to be ![]() when
when ![]() . (In Calculus we will learn an algebraic method for computing the exact maximum value of a function.) Rounding to two decimal places, we find the maximum volume obtainable under these conditions is about
. (In Calculus we will learn an algebraic method for computing the exact maximum value of a function.) Rounding to two decimal places, we find the maximum volume obtainable under these conditions is about ![]() cubic inches which occurs when the length and width of the square side of the box are approximately
cubic inches which occurs when the length and width of the square side of the box are approximately ![]() inches.[27]
inches.[27]

It is worth noting that while the function ![]() has a maximum, it did not have a minimum. Even though
has a maximum, it did not have a minimum. Even though ![]() for all
for all ![]() in its domain,[28] the presence of the hole at
in its domain,[28] the presence of the hole at ![]() means that
means that ![]() is not in the range of
is not in the range of ![]() . Hence, based on our model, we can never make a box with a `smallest’ volume.[29]
. Hence, based on our model, we can never make a box with a `smallest’ volume.[29]
Example 1.2.6 typifies the interplay between Algebra and Geometry which lies ahead. Both the algebraic description of ![]() :
: ![]() for
for ![]() , and the graph of
, and the graph of ![]() were useful in describing aspects of the physical situation at hand. Wherever possible, we’ll use the algebraic representations of functions to analytically produce exact answers to certain problems and use the graphical descriptions to check the reasonableness of our answers.
were useful in describing aspects of the physical situation at hand. Wherever possible, we’ll use the algebraic representations of functions to analytically produce exact answers to certain problems and use the graphical descriptions to check the reasonableness of our answers.
That being said, we’ll also encounter problems which we simply cannot answer analytically (such as determining the maximum volume in the previous example), so we will be forced to resort to using technology (specifically graphing technology) in order to find approximate solutions. The most important thing to keep in mind is that while technology may suggest a result, it is ultimately Mathematics that proves it.
We close this section with a summary of the different ways to represent functions.
Ways to Represent a Function
Suppose ![]() is a function with domain
is a function with domain ![]() . Then
. Then ![]() can be represented:
can be represented:
- verbally; that is, by describing how the inputs are matched with their outputs.
- using a mapping diagram.
- as a set of ordered pairs of the form (input, output):
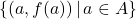 .
.
If ![]() is a function whose domain and range are subsets of real numbers, then
is a function whose domain and range are subsets of real numbers, then ![]() can be represented:
can be represented:
- algebraically as a formula for
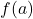 .
. - graphically by plotting the points
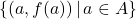 in the plane.
in the plane.
Note: An important consequence of the last bulleted item is that the point ![]() is on the graph of
is on the graph of ![]() if and only if
if and only if ![]()
1.2.4 Section Exercises
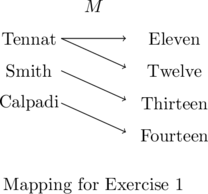
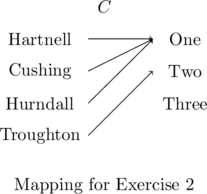
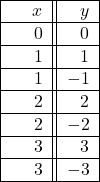
In Exercises 1 – 2, determine whether or not the mapping diagram represents a function. Explain your reasoning. If the mapping does represent a function, state the domain, range, and represent the function as a set of ordered pairs.
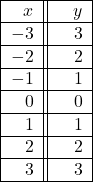
In Exercises 3 – 4, determine whether or not the data in the given table represents ![]() as a function of
as a function of ![]() . Explain your reasoning. If the mapping does represent a function, state the domain, range, and represent the function as a set of ordered pairs.
. Explain your reasoning. If the mapping does represent a function, state the domain, range, and represent the function as a set of ordered pairs.
-
- Suppose
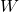 is the set of words in the English language and we set up a mapping from
is the set of words in the English language and we set up a mapping from 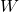 into the set of natural numbers
into the set of natural numbers 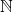 as follows: word
as follows: word  number of letters in the word. Explain why this mapping is a function. What would you need to know to determine the range of the function?
number of letters in the word. Explain why this mapping is a function. What would you need to know to determine the range of the function? - Suppose
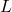 is the set of last names of all the people who have served or are currently serving as the President of the United States. Consider the mapping from
is the set of last names of all the people who have served or are currently serving as the President of the United States. Consider the mapping from 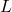 into
into 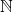 as follows: last name
as follows: last name  number of their presidency. For example, Washington
number of their presidency. For example, Washington 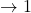 and Obama
and Obama 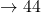 . Is this mapping a function? What if we use full names instead of just last names? (HINT: Research Grover Cleveland.)
. Is this mapping a function? What if we use full names instead of just last names? (HINT: Research Grover Cleveland.) - Under what conditions would the time of day be a function of the outdoor temperature?
For the functions ![]() described in Exercises 8 – 13, find
described in Exercises 8 – 13, find ![]() and find and simplify an expression for
and find and simplify an expression for ![]() that takes a real number
that takes a real number ![]() and performs the following three steps in the order given:
and performs the following three steps in the order given:
- (1) multiply by 2; (2) add 3; (3) divide by 4.
- (1) add 3; (2) multiply by 2; (3) divide by 4.
- (1) divide by 4; (2) add 3; (3) multiply by 2.
- (1) multiply by 2; (2) add 3; (3) take the square root.
- (1) add 3; (2) multiply by 2; (3) take the square root.
- (1) add 3; (2) take the square root; (3) multiply by 2.
In Exercises 14 – 19, use the given function ![]() to find and simplify the following:
to find and simplify the following:
In Exercises 20 – 25, use the given function ![]() to find and simplify the following:
to find and simplify the following:
In Exercises 26 – 29, use the given function ![]() to find
to find ![]() and solve
and solve ![]() .
.
In Exercises 30 – 44, determine whether or not the equation represents ![]() as a function of
as a function of ![]() .
.
Exercises 45 – 56 give a set of points in the ![]() -plane. Determine if
-plane. Determine if ![]() is a function of
is a function of ![]() . If so, state the domain and range.
. If so, state the domain and range.
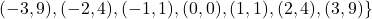
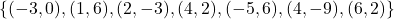
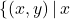 is an odd integer, and
is an odd integer, and  is an even integer
is an even integer
- \{
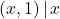 is an irrational number\}
is an irrational number\} 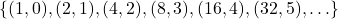
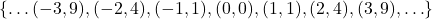
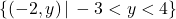
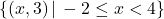
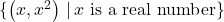
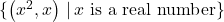
- The Vertical Line Test is a quick way to determine from a graph if the vertical axis variable is a function of the horizontal axis variable. If we are given a graph and asked to determine if the horizontal axis variable is a function of the vertical axis variable, we can use horizontal lines instead of vertical lines to check. Using Theorem 1.2 as a guide, formulate a `Horizontal Line Test.’ (We’ll refer back to this exercise in Section 5.1.)
In Exercises 58 – 61, determine whether or not the graph suggests ![]() is a function of
is a function of ![]() . For the ones which do, state the domain and range.
. For the ones which do, state the domain and range.
-
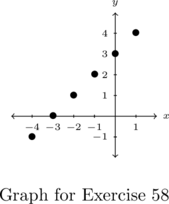
-
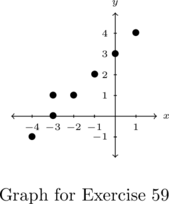
-
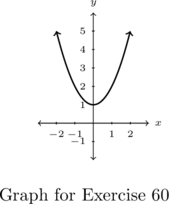
-
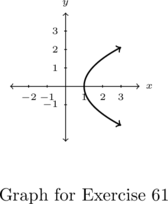
- Determine which, if any, of the graphs in numbers 58 – 61 represent
 as a function of
as a function of  . For the ones which do, state the domain and range. (Feel free to use Exercise 57.)
. For the ones which do, state the domain and range. (Feel free to use Exercise 57.)
In Exercises 63 – 66, determine whether or not the graph suggests ![]() is a function of
is a function of ![]() . For the ones which do, state the domain and range.
. For the ones which do, state the domain and range.
-
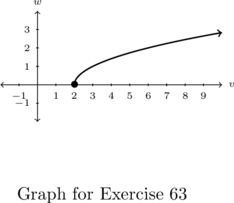
-
-
-

- Determine which, if any, of the graphs in numbers 63 – 66 represent
 as a function of
as a function of  . For the ones which do, state the domain and range. (Feel free to use Exercise 57.)
. For the ones which do, state the domain and range. (Feel free to use Exercise 57.)
In Exercises 68 – 71, determine whether or not the graph suggests ![]() is a function of
is a function of ![]() . For the ones which do, state the domain and range.
. For the ones which do, state the domain and range.
-
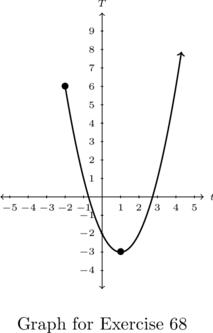
-
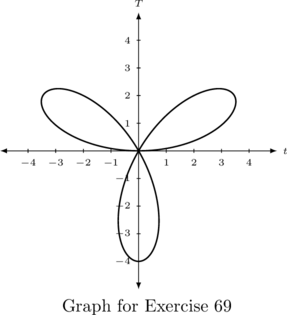
-

-
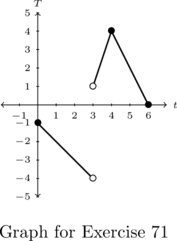
- Determine which, if any, of the graphs in numbers 68 – 71 represent
 as a function of
as a function of  . For the ones which do, state the domain and range. (Feel free to use Exercise 57.)
. For the ones which do, state the domain and range. (Feel free to use Exercise 57.)
In Exercises 73 – 76, determine whether or not the graph suggests ![]() is a function of
is a function of ![]() . For the ones which do, state the domain and range.
. For the ones which do, state the domain and range.
-
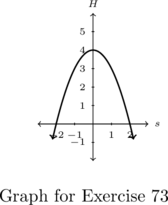
-
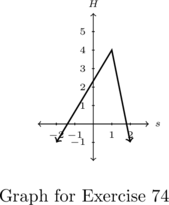
-
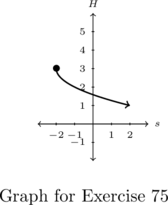
-
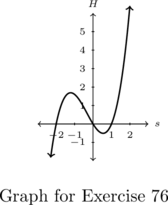
- Determine which, if any, of the graphs in numbers 73 – 76 represent
 as a function of
as a function of  . For the ones which do, state the domain and range. (Feel free to use Exercise 57.)
. For the ones which do, state the domain and range. (Feel free to use Exercise 57.)
In Exercises 78 – 81, determine whether or not the graph suggests ![]() is a function of
is a function of ![]() . For the ones which do, state the domain and range.
. For the ones which do, state the domain and range.
-

-
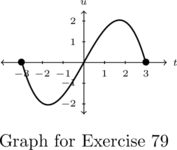
-
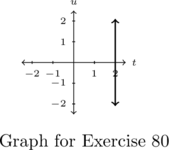
-
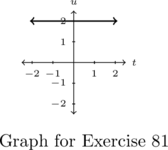
- Determine which, if any, of the graphs in numbers 78 – 81 represent
 as a function of
as a function of 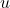 . For the ones which do, state the domain and range. (Feel free to use Exercise 57.)
. For the ones which do, state the domain and range. (Feel free to use Exercise 57.)
In Exercises 83 – 92, use the graphs of ![]() and
and ![]() below to find the indicated values.
below to find the indicated values.
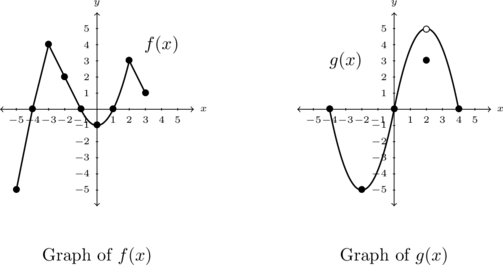
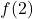
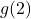
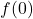
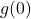
- Solve
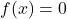 .
. - Solve
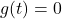 .
. - State the domain and range of
 .
. - State the domain and range of
 .
.
In Exercises 93 – 104, graph each function by making a table and plotting points. Use the independent variable as the horizontal axis label and the default `![]() ‘ label for the vertical axis label. State the domain and range of each function.
‘ label for the vertical axis label. State the domain and range of each function.
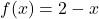
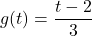
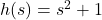
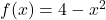
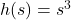
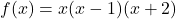
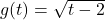
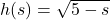
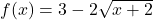
![Rendered by QuickLaTeX.com g(t) = \sqrt[3]{t}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7c7e24d89d18511552e695969d277dde_l3.png)
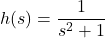
- Consider the function
 described below:
described below:
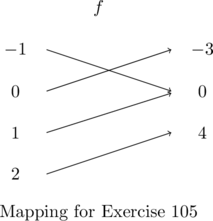
- State the domain and range of
 .
. - Find
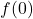 and solve
and solve 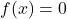 .
. - Write
 as a set of ordered pairs.
as a set of ordered pairs. - Graph
 .
.
- State the domain and range of
- Let
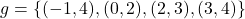
- State the domain and range of
 .
. - Create a mapping diagram for
 .
. - Find
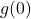 and solve
and solve 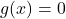 .
. - Graph
 .
.
- State the domain and range of
- Let
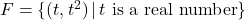 . Find
. Find 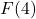 and solve
and solve 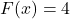 .
.
HINT: Elements of are of the form
are of the form 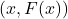 .
. - Let
 . Find
. Find  and solve
and solve  .
.
HINT: Elements of are of the form
are of the form 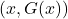 .
. - The area enclosed by a square, in square inches, is a function of the length of one of its sides
 , when measured in inches. This function is represented by the formula
, when measured in inches. This function is represented by the formula 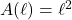 for
for 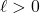 . Find
. Find 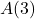 and solve
and solve 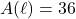 . Interpret your answers to each. Why is
. Interpret your answers to each. Why is 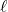 restricted to
restricted to 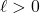 ?
? - The area enclosed by a circle, in square meters, is a function of its radius
 , when measured in meters. This function is represented by the formula
, when measured in meters. This function is represented by the formula 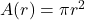 for
for  . Find
. Find 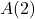 and solve
and solve 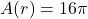 . Interpret your answers to each. Why is
. Interpret your answers to each. Why is  restricted to
restricted to 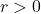 ?
? - The volume enclosed by a cube, in cubic centimeters, is a function of the length of one of its sides
 , when measured in centimeters. This function is represented by the formula
, when measured in centimeters. This function is represented by the formula 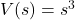 for
for 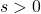 . Find
. Find 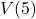 and solve
and solve 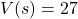 . Interpret your answers to each. Why is
. Interpret your answers to each. Why is  restricted to
restricted to 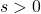 ?
? - The volume enclosed by a sphere, in cubic feet, is a function of the radius of the sphere
 , when measured in feet. This function is represented by the formula
, when measured in feet. This function is represented by the formula 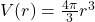 for
for 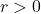 . Find
. Find 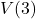 and solve
and solve 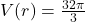 . Interpret your answers to each. Why is
. Interpret your answers to each. Why is  restricted to
restricted to  ?
? - The height of an object dropped from the roof of an eight story building is modeled by the function:
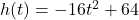 ,
, 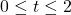 . Here,
. Here, 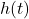 is the height of the object off the ground, in feet,
is the height of the object off the ground, in feet,  seconds after the object is dropped. Find
seconds after the object is dropped. Find 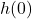 and solve
and solve 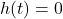 . Interpret your answers to each. Why is
. Interpret your answers to each. Why is  restricted to
restricted to 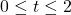 ?
? - The temperature in degrees Fahrenheit
 hours after 6 AM is given by
hours after 6 AM is given by 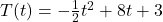 for
for 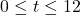 . Find and interpret
. Find and interpret 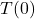 ,
, 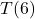 and
and 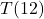 .
. - The function
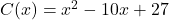 models the cost, in hundreds of dollars, to produce
models the cost, in hundreds of dollars, to produce  thousand pens. Find and interpret
thousand pens. Find and interpret  ,
, 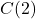 and
and 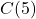 .
. - Using data from the Bureau of Transportation Statistics, the average fuel economy in miles per gallon for passenger cars in the US can be modeled by
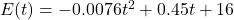 ,
,  , where
, where  is the number of years since
is the number of years since 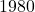 . Use a calculator to find
. Use a calculator to find 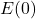 ,
, 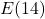 and
and 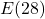 . Round your answers to two decimal places and interpret your answers to each.
. Round your answers to two decimal places and interpret your answers to each. - The perimeter of a square, in centimeters, is four times the length of one if its sides, also measured in centimeters. Represent the function
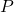 which takes as its input the length of the side of a square in centimeters,
which takes as its input the length of the side of a square in centimeters,  and returns the perimeter of the square in inches,
and returns the perimeter of the square in inches, 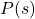 using a formula.
using a formula. - The circumference of a circle, in feet, is
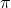 times the diameter of the circle, also measured in feet. Represent the function
times the diameter of the circle, also measured in feet. Represent the function 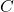 which takes as its input the length of the diameter of a circle in feet,
which takes as its input the length of the diameter of a circle in feet, 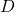 and returns the circumference of a circle in inches,
and returns the circumference of a circle in inches, 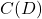 using a formula.
using a formula. - Suppose
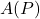 gives the amount of money in a retirement account (in dollars) after 30 years as a function of the amount of the monthly payment (in dollars),
gives the amount of money in a retirement account (in dollars) after 30 years as a function of the amount of the monthly payment (in dollars), 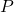 .
.
- What does
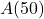 mean?
mean? - What is the significance of the solution to the equation
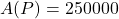 ?
? - Explain what each of the following expressions mean:
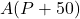 ,
, 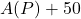 , and
, and 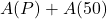 .
.
- What does
- Suppose
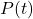 gives the chance of precipitation (in percent)
gives the chance of precipitation (in percent)  hours after 8 AM.
hours after 8 AM.
- Write an expression which gives the chance of precipitation at noon.
- Write an inequality which determines when the chance of precipitation is more than
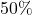 .
.
- Explain why the graph in Exercise 63 suggests that not only is
 as a function of
as a function of 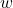 but also
but also 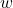 is a function of
is a function of  . Suppose
. Suppose 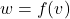 and
and 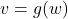 . That is,
. That is,  is the name of the function which takes
is the name of the function which takes  values as inputs and returns
values as inputs and returns  values as outputs and
values as outputs and  is the name of the function which does vice-versa. Find the domain and range of
is the name of the function which does vice-versa. Find the domain and range of  and compare these to the domain and range of
and compare these to the domain and range of  .
. - Sketch the graph of a function with domain
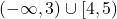 with range
with range 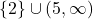 .
.
Section 1.2 Exercise Answers can be found in the Appendix … Coming soon
- Please refer to Section 0.4 for a review of this terminology. ↵
- Please refer to Section 0.4 for a review of the terminology used in these definitions. ↵
- For purposes of completeness, the set
 is called the codomain of
is called the codomain of  . For us, the concepts of domain and range suffice as our codomain will most always be the set of real numbers,
. For us, the concepts of domain and range suffice as our codomain will most always be the set of real numbers,  . ↵
. ↵ - If instead of mapping
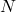 into
into 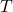 , we could have mapped
, we could have mapped 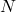 into
into 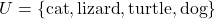 in which case the range of
in which case the range of  would not have been the entire codomain
would not have been the entire codomain 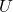 . ↵
. ↵ - These adjectives stem from the fact that the value of
 depends entirely on our (independent) choice of
depends entirely on our (independent) choice of 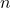 . ↵
. ↵ - Specifically,
 is a function so it requires and domain, a range and a rule of assignment whereas
is a function so it requires and domain, a range and a rule of assignment whereas  is simply the output from
is simply the output from  . ↵
. ↵ - In fact, it is not uncommon to see the name of the function as the same as the dependent variable. For example, writing `
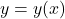 ' would be a way to communicate the idea that `
' would be a way to communicate the idea that ` is a function of
is a function of  '. ↵
'. ↵ - You may be wondering why one would ever compute these quantities. Rest assured that we will use expressions like these in examples throughout the text. For now, it suffices just to know that they are different. ↵
- also called the `global' minimum ↵
- also called the `global' maximum ↵
- also called the `global' extrema or the `extreme values' ↵
- You may need to review Section 0.3. ↵
- As was mentioned before, we will give meanings to the these quantities in other examples throughout the text. ↵
- Said differently,
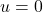 is not in the domain of the function represented by the equation
is not in the domain of the function represented by the equation 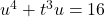 . ↵
. ↵ - Try it for yourself! ↵
- One major use of Calculus is to optimize functions analytically - that is, without a graph. ↵
- Roughly speaking, a continuous variable is a variable which takes on values over an interval of real numbers as opposed to values in a discrete list. In this case we would think of time as a `continuum' - an interval of real numbers as opposed to
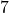 or so isolated times. A continuous function is a function which takes an interval of real numbers and maps it in such a way that its graph is a connected curve with no holes or gaps. This is technically a Calculus idea, but we'll need to discuss the notion of continuity a few times in the text. ↵
or so isolated times. A continuous function is a function which takes an interval of real numbers and maps it in such a way that its graph is a connected curve with no holes or gaps. This is technically a Calculus idea, but we'll need to discuss the notion of continuity a few times in the text. ↵ - Please consult Section 0.4 for a review of interval notation if need be. ↵
- For all we know, it could be
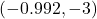 . ↵
. ↵ - That is, the horizontal axis is labeled with `
 ' and the vertical axis is labeled with `
' and the vertical axis is labeled with ` '. ↵
'. ↵ - The curve in this example is called a `parabola'. In Section 2.1, we'll learn how to graph these accurately by hand. ↵
- See here. ↵
- We'll skip the explanation for now because we want to focus on just the different representations of the function. Rest assured, you'll be asked to construct this very model in an Exercise in Section 2.2. ↵
- Note that we have
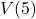 and
and 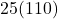 in the same string of equality. The first set of parentheses is function notation and directs us to substitute
in the same string of equality. The first set of parentheses is function notation and directs us to substitute 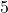 for
for  in the expression
in the expression 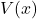 while the second indicates multiplying
while the second indicates multiplying 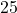 by
by 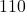 . Context is key! ↵
. Context is key! ↵ - If
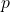 is any positive real number,
is any positive real number, 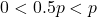 , so we can always find a smaller positive real number. ↵
, so we can always find a smaller positive real number. ↵ - What's really needed here is the precise definition of `closeness' discussed in Calculus. This hand-waving will do for now. ↵
- We could also find the length of the box in this case as well. The sum of length and girth is 130 inches so the length is 130 minus the girth, or
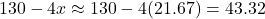 inches. ↵
inches. ↵ - said differently, the values of
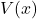 are bounded below by
are bounded below by  . ↵
. ↵ - How realistic is this? ↵
A process by which elements of one set are matched with elements from another set.
A process by which each element from one set is matched with one and only one element from another set.
The domain of a function is the set of inputs for the function.
The range of a function is the set of outputs of the function.
The smallest value in the range, such that all other values are greater than or equal to that value.
The largest value in the range of a function, such that all other range values are less than or equal to value.
The absolute minimum or absolute maximum for a function.
A function is increasing on an interval if as the inputs increase, the outputs increase.
A function is decreasing on an interval if as the inputs increase, the outputs decrease.
A function is constant on an interval if it has the same output value for all inputs in the interval.
A function is even if the value of the function is the same for both x and -x.
A function is odd if the value of the function at -x is opposite the value of the function at x.