1.5 Function Arithmetic
1.5.1 Function Arithmetic
In this section, we begin our study of what can be considered as the algebra of functions by defining function arithmetic.
Given two real numbers, we have four primary arithmetic operations available to us: addition, subtraction, multiplication, and division (provided we don’t divide by ![]() .) As the functions we study in this text have ranges which are sets of real numbers, it makes sense we can extend these arithmetic notions to functions.
.) As the functions we study in this text have ranges which are sets of real numbers, it makes sense we can extend these arithmetic notions to functions.
For example, to add two functions means we add their outputs; to subtract two functions, we subtract their outputs, and so on and so forth. More formally, given two functions ![]() and
and ![]() , we define a new function
, we define a new function ![]() whose rule is determined by adding the outputs of
whose rule is determined by adding the outputs of ![]() and
and ![]() . That is
. That is ![]() . While this looks suspiciously like some kind of distributive property, it is nothing of the sort. The `
. While this looks suspiciously like some kind of distributive property, it is nothing of the sort. The `![]() ‘ sign in the expression `
‘ sign in the expression `![]() ‘ is part of the name of the function we are defining,[1] whereas the plus sign `
‘ is part of the name of the function we are defining,[1] whereas the plus sign `![]() ‘ sign in the expression
‘ sign in the expression ![]() represents real number addition: we are adding the output from
represents real number addition: we are adding the output from ![]() ,
, ![]() with the output from
with the output from ![]() ,
, ![]() to determine the output from the sum function,
to determine the output from the sum function, ![]() .
.
Of course, in order to define ![]() by the formula
by the formula ![]() , both
, both ![]() and
and ![]() need to be defined in the first place; that is,
need to be defined in the first place; that is, ![]() must be in the domain of
must be in the domain of ![]() and the domain of
and the domain of ![]() . You’ll recall[2] this means
. You’ll recall[2] this means ![]() must be in the intersection of the domains of
must be in the intersection of the domains of ![]() and
and ![]() . We define the following.
. We define the following.
Definition 1.13
Suppose ![]() and
and ![]() are functions and
are functions and ![]() is in both the domain of
is in both the domain of ![]() and the domain of
and the domain of ![]() .
.
- The sum of
 and
and  , denoted
, denoted 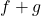 , is the function defined by the formula
, is the function defined by the formula
![Rendered by QuickLaTeX.com \[(f+g)(x) = f(x) + g(x)\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-37af130c48993951bd8d65f64254f767_l3.png)
- The difference of
 and
and  , denoted
, denoted  , is the function defined by the formula
, is the function defined by the formula
![Rendered by QuickLaTeX.com \[(f-g)(x) = f(x) - g(x)\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-003ebc14d71750695b705811dd08a9ac_l3.png)
- The product of
 and
and  , denoted
, denoted 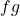 , is the function defined by the formula
, is the function defined by the formula
![Rendered by QuickLaTeX.com \[(fg)(x) = f(x)g(x)\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-ae1736ea46272a6638d9e7c737f06632_l3.png)
- The quotient of
 and
and  , denoted
, denoted 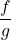 , is the function defined by the formula
, is the function defined by the formula
![Rendered by QuickLaTeX.com \[\left(\dfrac{f}{g}\right)(x) = \dfrac{f(x)}{g(x)}, \text{ provided } g(x) \neq 0.\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7ad379642e48d371c0729470febfc9fe_l3.png)
We put these definitions to work for us in the next example.
Example 1.5.1
Example 1.5.1.1a
Consider the following functions:
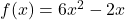
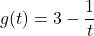 ,
, 
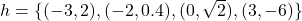
 whose graph is given below:
whose graph is given below:
Compute and simplify the following function values:
![]()
Solution:
Compute and simplify ![]() .
.
By definition, ![]() .
.
We find ![]() and
and ![]() .
.
So we get
![]()
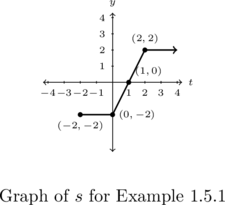
Example 1.5.1.1b
Consider the following functions:
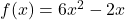
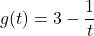 ,
, 
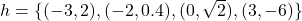
 whose graph is given below:
whose graph is given below:

Compute and simplify the following function values:
![]()
Solution:
Compute and simplify ![]() .
.
To find ![]() , we need both
, we need both ![]() and
and ![]() .
.
To get ![]() , we look to the graph of
, we look to the graph of ![]() and look for the
and look for the ![]() -coordinate of the point on the graph with the
-coordinate of the point on the graph with the ![]() -coordinate of
-coordinate of ![]() . While not labeled directly, we infer the point
. While not labeled directly, we infer the point ![]() is on the graph which means
is on the graph which means ![]() .
.
For ![]() , we compute:
, we compute: ![]() .
.
Putting it all together, we get
![]()
Example 1.5.1.1c
Consider the following functions:
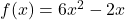
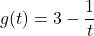 ,
, 
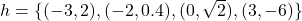
 whose graph is given below:
whose graph is given below:

Compute and simplify the following function values:
![]()
Solution:
Compute and simplify ![]() .
.
Because ![]() , we first compute
, we first compute ![]() and
and ![]() .
.
We find ![]() and
and ![]() .
.
So
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} (fg)(2) &=& f(2) g(2) \\ &=& (20)\left(\frac{5}{2}\right) \\ &=& 50. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9829b6939bcb13cc1d9817ccb3f2c136_l3.png)
Example 1.5.1.1d
Consider the following functions:
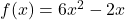
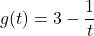 ,
, 
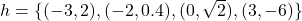
 whose graph is given below:
whose graph is given below:

Compute and simplify the following function values:
![]()
Solution:
Compute and simplify ![]() .
.
By definition, ![]() .
.
As ![]() is on the graph of
is on the graph of ![]() , we know
, we know ![]() .
.
Likewise, the ordered pair ![]() , so
, so ![]() .
.
We get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \left( \frac{s}{h} \right)(0) &=& \frac{s(0)}{h(0)} \\ &=& \frac{-2}{\sqrt{2}} \\ &=& -\sqrt{2}. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-8e4c968170908bac4534a68862853316_l3.png)
Example 1.5.1.1e
Consider the following functions:
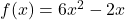
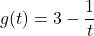 ,
, 
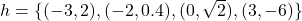
 whose graph is given below:
whose graph is given below:

Compute and simplify the following function values:
![]()
Solution:
Compute and simplify ![]() .
.
The expression ![]() involves three functions. Fortunately, they are grouped so that we can apply Definition 1.13 by first considering the sum of the two functions
involves three functions. Fortunately, they are grouped so that we can apply Definition 1.13 by first considering the sum of the two functions ![]() and
and ![]() , then to the sum of the two functions
, then to the sum of the two functions ![]() and
and ![]() :
: ![]() .
.
To get ![]() , we look to the graph of
, we look to the graph of ![]() . We infer the point
. We infer the point ![]() is on the graph of
is on the graph of ![]() , so
, so ![]() .
.
We compute ![]() .
.
To find ![]() , we note
, we note ![]() , so
, so ![]() .
.
Hence,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} ((s+g)+h)(3) &=& (s+g)(3)+h(3) \\ &=& (s(3)+g(3))+h(3) \\ &=& \left(2+\frac{8}{3}\right) + (-6) \\ &=& -\frac{4}{3}. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-12a4ae1f055928abc5e20a91de8ba0b0_l3.png)
Example 1.5.1.1f
Consider the following functions:
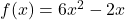
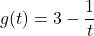 ,
, 
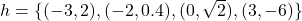
 whose graph is given below:
whose graph is given below:

Compute and simplify the following function values:
![]()
Solution:
Compute and simplify ![]() .
.
The expression ![]() is very similar to the previous problem,
is very similar to the previous problem, ![]() except that the
except that the ![]() and
and ![]() are grouped together here instead of the
are grouped together here instead of the ![]() and
and ![]() .
.
We proceed as above applying Definition 1.13 twice and find ![]() .
.
Substituting the values for ![]() ,
, ![]() and
and ![]() , we get
, we get ![]() , which, not surprisingly, matches our answer to the previous problem.
, which, not surprisingly, matches our answer to the previous problem.
Example 1.5.1.1g
Consider the following functions:
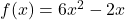
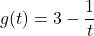 ,
, 
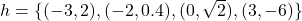
 whose graph is given below:
whose graph is given below:

Compute and simplify the following function values:
![]()
Solution:
Compute and simplify ![]() .
.
Once again, we find the expression ![]() has more than two functions involved. As with all fractions, we treat `
has more than two functions involved. As with all fractions, we treat `![]() ‘ as a grouping symbol and interpret
‘ as a grouping symbol and interpret ![]() .
.
We compute ![]() and have
and have ![]() and
and ![]() from above.
from above.
Hence,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl}\left(\frac{f+h}{s}\right)(3) &=& \frac{f(3)+h(3)}{s(3)} \\ &=& \frac{48+(-6)}{2}\\ &=& 21. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d43621d1de7d63770efd782c77ef8313_l3.png)
Example 1.5.1.1h
Consider the following functions:
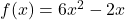
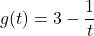 ,
, 
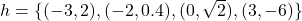
 whose graph is given below:
whose graph is given below:

Compute and simplify the following function values:
![]()
Solution:
Compute and simplify ![]() .
.
We need to need to exercise caution in parsing ![]() . In this context,
. In this context, ![]() ,
, ![]() , and
, and ![]() are all functions, so we interpret
are all functions, so we interpret ![]() as the function and
as the function and ![]() as the argument. We view the function
as the argument. We view the function ![]() as the product of
as the product of ![]() and the function
and the function ![]() .
.
Hence, ![]() .
.
We compute ![]() , and
, and ![]() . Because
. Because ![]() ,
, ![]() .
.
Putting this altogether, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} (f(g-h))(-2) &=& f(-2) [(g-h)(-2)] \\ &=& f(-2) [g(-2) - h(-2)] \\ &=& 28(3.5-0.4) \\ &=& 28(3.1)\\ &=& 86.8. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-966d7aa505b8bc7c51c418928ba9a654_l3.png)
Example 1.5.1.2a
Consider the following functions:
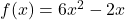
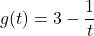 ,
, 
 whose graph is given below:
whose graph is given below:

State the domain of each of the following functions:
![]()
Solution:
State the domain of ![]() .
.
To find the domain of ![]() , we need to find the real numbers in both the domain of
, we need to find the real numbers in both the domain of ![]() and the domain of
and the domain of ![]() .
.
The domain of ![]() is
is ![]() and the domain of
and the domain of ![]() is
is ![]() so the only real number in common here is
so the only real number in common here is ![]() .
.
Hence, the domain of ![]() is
is ![]() , which may be small, but it’s better than nothing.[3]
, which may be small, but it’s better than nothing.[3]
Example 1.5.1.2b
Consider the following functions:
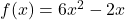
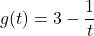 ,
, 
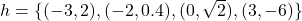
 whose graph is given below:
whose graph is given below:

State the domain of each of the following functions:
![]()
Solution:
State the domain of ![]() .
.
To find the domain of ![]() , we first note the domain of
, we first note the domain of ![]() is all real numbers, but that the domain of
is all real numbers, but that the domain of ![]() , based on the graph, is just
, based on the graph, is just ![]() .
.
Moreover, ![]() when
when ![]() , so we must exclude this value from the domain of
, so we must exclude this value from the domain of ![]() .
.
Hence, we are left with ![]() .
.
Example 1.5.1.3a
Consider the following functions:
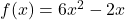
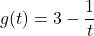 ,
, 
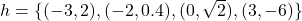
 whose graph is given below:
whose graph is given below:

Determine expressions for the functions below. State the domain for each.
![]()
Solution:
Determine an expression for ![]() . Then state the domain of the function.
. Then state the domain of the function.
By definition, ![]() .
.
We are given ![]() and
and ![]() so
so ![]() . Hence,
. Hence,
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} (fg)(x) & = & f(x)g(x) & \\ & = & \left( 6x^2-2x \right) \left( 3 - \dfrac{1}{x} \right) & \\ & = & 6x^2(3) - 6x^2 \left(\dfrac{1}{x}\right) - 2x(3) + 2x \left(\dfrac{1}{x}\right) & \text{distribute} \\ & = & 18x^2 - 6x - 6x + 2 & \\ & = & 18x^2 - 12x + 2 & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d6db83b719b82cce7b28b3f4ed73fa0f_l3.png)
To find the domain of ![]() , we note the domain of
, we note the domain of ![]() is all real numbers,
is all real numbers, ![]() whereas the domain of
whereas the domain of ![]() is restricted to
is restricted to ![]() .
.
Hence, the domain of ![]() is likewise restricted to
is likewise restricted to ![]() .
.
Note if we relied solely on the simplified formula for ![]() , we would have obtained the incorrect answer for the domains of
, we would have obtained the incorrect answer for the domains of ![]() .
.
Example 1.5.1.3b
Consider the following functions:
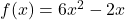
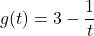 ,
, 
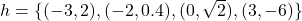
 whose graph is given below:
whose graph is given below:

Determine expressions for the functions below. State the domain for each.
![]()
Solution:
Determine an expression for ![]() . Then state the domain of the function.
. Then state the domain of the function.
To find an expression for ![]() we first note
we first note ![]() and
and ![]() .
.
Hence:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \left( \dfrac{g}{f}\right)(t) & = & \dfrac{g(t)}{f(t)} & \\ & = & \dfrac{3-\dfrac{1}{t}}{6t^2 - 2t} & \\[12pt] &=& \dfrac{3-\dfrac{1}{t}}{6t^2 - 2t} \cdot \dfrac{t}{t} & \text{simplify compound fractions} \\[12pt] & = & \dfrac{\left(3-\dfrac{1}{t}\right) t}{\left(6t^2 - 2t\right)t} & \\[12pt] &=& \dfrac{3t-1}{\left(6t^2 - 2t\right)t} & \\[12pt] & = & \dfrac{3t-1}{2t^2(3t-1)} & \\[12pt] &=& \dfrac{\cancelto{1}{(3t-1)}}{2t^2\cancel{(3t-1)}} & \text{factor and divide out} \\[12pt] & = & \dfrac{1}{2t^2} & \text{provided } t\neq \dfrac{1}{3} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-bedff4778c25119979871311f0ceb0af_l3.png)
A few remarks are in order. First, in number 1 parts 1e through 1h, we first encountered combinations of three functions despite Definition 1.13 only addressing combinations of two functions at a time. It turns out that function arithmetic inherits many of the same properties of real number arithmetic. For example, we showed above that ![]() . In general, given any three functions
. In general, given any three functions ![]() ,
, ![]() , and
, and ![]() ,
, ![]() that is, function addition is assocative. To see this, choose an element
that is, function addition is assocative. To see this, choose an element ![]() common to the domains of
common to the domains of ![]() ,
, ![]() , and
, and ![]() . Then
. Then
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} ((f+g)+h)(x) & = & (f+g)(x)+h(x) & \text{definiton of $((f+g)+h)(x)$} \\ & = & (f(x)+g(x))+h(x) & \text{definition of $(f+g)(x)$} \\ & = & f(x) + (g(x)+h(x)) & \text{associative property of real number addition} \\ & = & f(x) + (g+h)(x) & \text{definition of $(g+h)(x)$} \\ & = & (f+(g+h))(x) & \text{definition of $(f+(g+h))(x)$} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-04bfde649d0b1b233c17d8aafdc594f9_l3.png)
The key step to the argument is that ![]() which is true courtesy of the associative property of real number addition. And just like with real number addition, because function addition is associative, we may write
which is true courtesy of the associative property of real number addition. And just like with real number addition, because function addition is associative, we may write ![]() instead of
instead of ![]() or
or ![]() even though, when it comes down to computations, we can only add two things together at a time.[4]
even though, when it comes down to computations, we can only add two things together at a time.[4]
For completeness, we summarize the properties of function arithmetic in the theorem below. The proofs of the properties all follow along the same lines as the proof of the associative property and are left to the reader. We investigate some additional properties in the exercises.
Theorem 1.5
Suppose ![]() ,
, ![]() and
and ![]() are functions.
are functions.
- Commutative Law of Addition:
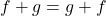
- Associative Law of Addition:
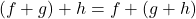
- Additive Identity: The function
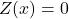 satisfies:
satisfies: 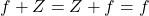 for all functions
for all functions  .
. - Additive Inverse: The function
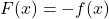 for all
for all  in the domain of
in the domain of  satisfies:
satisfies:
![Rendered by QuickLaTeX.com \[ f+F=F+f=Z.\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b6b8ce2223d276afd8d96ade646aea9e_l3.png)
- Commutative Law of Multiplication:
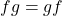
- Associative Law of Multiplication:
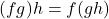
- Multiplicative Identity: The function
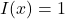 satisfies:
satisfies: 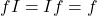 for all functions
for all functions  .
. - Multiplicative Inverse: If
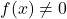 for all
for all  in the domain of
in the domain of  , then
, then 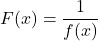 satisfies:
satisfies:
![Rendered by QuickLaTeX.com \[ fF=Ff = I\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-8884fdba81a0751869e6f73d3a52c608_l3.png)
- Distributive Law of Multiplication over Addition:
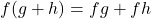
In the next example, we decompose given functions into sums, differences, products and/or quotients of other functions. Note that there are infinitely many different ways to do this, including some trivial ones. For example, suppose we were instructed to decompose ![]() into a sum or difference of functions. We could write
into a sum or difference of functions. We could write ![]() where
where ![]() and
and ![]() or we could choose
or we could choose ![]() and
and ![]() . More simply, we could write
. More simply, we could write ![]() where
where ![]() and
and ![]() . We’ll call this last decomposition a `trivial’ decomposition. Likewise, if we ask for a decomposition of
. We’ll call this last decomposition a `trivial’ decomposition. Likewise, if we ask for a decomposition of ![]() as a product, a nontrivial solution would be
as a product, a nontrivial solution would be ![]() where
where ![]() and
and ![]() whereas a trivial solution would be
whereas a trivial solution would be ![]() and
and ![]() . In general, non-trivial solutions to decomposition problems avoid using the additive identity,
. In general, non-trivial solutions to decomposition problems avoid using the additive identity, ![]() , for sums and differences and the multiplicative identity,
, for sums and differences and the multiplicative identity, ![]() , for products and quotients.
, for products and quotients.
Example 1.5.2
Example 1.5.2.1a
For ![]() , find functions
, find functions ![]() ,
, ![]() and
and ![]() to decompose
to decompose ![]() nontrivially as:
nontrivially as:
![]()
Solution:
Decompose ![]() .
.
To decompose ![]() , we need functions
, we need functions ![]() and
and ![]() so
so ![]() .
.
Given ![]() , one option is to let
, one option is to let ![]() and
and ![]() .
.
To check, we find ![]() as required. In addition to checking the formulas match up, we also need to check domains.
as required. In addition to checking the formulas match up, we also need to check domains.
There isn’t much work here as the domains of ![]() and
and ![]() are all real numbers which combine to give the domain of
are all real numbers which combine to give the domain of ![]() which is all real numbers.
which is all real numbers.
Example 1.5.2.1b
For ![]() , find functions
, find functions ![]() ,
, ![]() and
and ![]() to decompose
to decompose ![]() nontrivially as:
nontrivially as:
![]()
Solution:
Decompose ![]() .
.
In order to write ![]() , we need
, we need ![]() .
.
One way to accomplish this is to write ![]() and identify
and identify ![]() and
and ![]() .
.
To check, ![]() .
.
Again, the domains for both ![]() and
and ![]() are all real numbers which combine to give
are all real numbers which combine to give ![]() its domain of all real numbers.
its domain of all real numbers.
Example 1.5.2.1c
For ![]() , find functions
, find functions ![]() ,
, ![]() and
and ![]() to decompose
to decompose ![]() nontrivially as:
nontrivially as:
![]()
Solution:
Decompose ![]() .
.
To write ![]() , we require
, we require ![]() .
.
In other words, we need to factor ![]() . We find
. We find ![]() , so one choice is to select
, so one choice is to select ![]() and
and ![]() . Then
. Then ![]() as required.
as required.
As above, the domains of ![]() and
and ![]() are all real numbers which combine to give
are all real numbers which combine to give ![]() the correct domain of
the correct domain of ![]() .
.
Example 1.5.2.1d
For ![]() , find functions
, find functions ![]() ,
, ![]() and
and ![]() to decompose
to decompose ![]() nontrivially as:
nontrivially as:
![]()
Solution:
Decompose ![]() .
.
We need to be careful here interpreting the equation ![]() . What we have is an equality of functions so the parentheses here do not represent function notation here, but, rather function multiplication. The way to parse
. What we have is an equality of functions so the parentheses here do not represent function notation here, but, rather function multiplication. The way to parse ![]() , then, is the function
, then, is the function ![]() times the function
times the function ![]() . Hence, we seek functions
. Hence, we seek functions ![]() ,
, ![]() , and
, and ![]() so that
so that ![]() .
.
From the previous example, we know we can rewrite ![]() , so one option is to set
, so one option is to set ![]() and
and ![]() so that
so that
![]()
as required.
As above, the domain of all constituent functions is ![]() which matches the domain of
which matches the domain of ![]() .
.
Example 1.5.2.2a
For ![]() , find functions
, find functions ![]() ,
, ![]() and
and ![]() to decompose
to decompose ![]() nontrivially as:
nontrivially as:
![]()
Solution:
Decompose ![]() .
.
To write ![]() , we need
, we need ![]() and
and ![]() so
so ![]() .
.
We choose ![]() and
and ![]() . Sure enough,
. Sure enough, ![]() as required.
as required.
When it comes to the domain of ![]() , owing to the square root, we require
, owing to the square root, we require ![]() . We have a denominator as well, therefore we require
. We have a denominator as well, therefore we require ![]() . The former requirement is the same restriction on
. The former requirement is the same restriction on ![]() , and the latter requirement comes from Definition 1.13. Starting with the domain of
, and the latter requirement comes from Definition 1.13. Starting with the domain of ![]() , all real numbers, and working through the details, we arrive at the correct domain of
, all real numbers, and working through the details, we arrive at the correct domain of ![]() ,
, ![]() .
.
Example 1.5.2.2b
For ![]() , find functions
, find functions ![]() ,
, ![]() and
and ![]() to decompose
to decompose ![]() nontrivially as:
nontrivially as:
![]()
Solution:
Decompose ![]() .
.
Next, we are asked to find functions ![]() and
and ![]() so
so ![]() . This means we need to rewrite the expression for
. This means we need to rewrite the expression for ![]() as a product. One way to do this is to convert radical notation to exponent notation:
as a product. One way to do this is to convert radical notation to exponent notation:
![]()
Choosing ![]() and
and ![]() , we see
, we see ![]() as required.
as required.
The domain restrictions on ![]() stem from the presence of the square root in the denominator – both are addressed when finding the domain of
stem from the presence of the square root in the denominator – both are addressed when finding the domain of ![]() . Hence, we obtain the correct domain of
. Hence, we obtain the correct domain of ![]() as
as ![]() .
.
Example 1.5.2.2c
For ![]() , find functions
, find functions ![]() ,
, ![]() and
and ![]() to decompose
to decompose ![]() nontrivially as:
nontrivially as:
![]()
Solution:
Decompose ![]() .
.
To express ![]() as a sum of functions
as a sum of functions ![]() and
and ![]() , we could rewrite
, we could rewrite
![]()
so that ![]() and
and ![]() .
.
Indeed, ![]() , as required.
, as required.
Moreover, the domain restrictions for ![]() are the same for both
are the same for both ![]() and
and ![]() , so we get agreement on the domain being
, so we get agreement on the domain being ![]() .
.
Example 1.5.2.2d
For ![]() , find functions
, find functions ![]() ,
, ![]() and
and ![]() to decompose
to decompose ![]() nontrivially as:
nontrivially as:
![]()
Solution:
Decompose ![]() .
.
Last, but not least, to write ![]() , we require
, we require ![]() .
.
Identifying ![]() ,
, ![]() , and
, and ![]() , we get
, we get
![]()
Concerning domains, the domain of both ![]() and
and ![]() are all real numbers, but the domain of
are all real numbers, but the domain of ![]() is restricted to
is restricted to ![]() . Coupled with the restriction stated in Definition 1.13 that
. Coupled with the restriction stated in Definition 1.13 that ![]() , we recover the domain of
, we recover the domain of ![]() ,
, ![]() .
.
1.5.2 Function Composition
We just saw how the arithmetic of real numbers carried over into an arithmetic of functions. In this section, we discuss another way to combine functions which is unique to functions and isn’t shared with real numbers – function composition.
Definition 1.14
Let ![]() and
and ![]() be functions where the real number
be functions where the real number ![]() is in the domain of
is in the domain of ![]() and the real number
and the real number ![]() is in the domain of
is in the domain of ![]() . The composite of
. The composite of ![]() with
with ![]() , denoted
, denoted ![]() , and read `
, and read `![]() composed with
composed with ![]() ‘ is defined by the formula:
‘ is defined by the formula: ![]() .
.
To compute ![]() , we use the formula given in Defintion 1.14:
, we use the formula given in Defintion 1.14: ![]() . However, from a procedural viewpoint, Defintion 1.14 tells us the output from
. However, from a procedural viewpoint, Defintion 1.14 tells us the output from ![]() is found by taking the output from
is found by taking the output from ![]() ,
, ![]() , and then making that the input to
, and then making that the input to ![]() . From this perspective, we see
. From this perspective, we see ![]() as a two step process taking an input
as a two step process taking an input ![]() and first applying the procedure
and first applying the procedure ![]() then applying the procedure
then applying the procedure ![]() . Abstractly, we have
. Abstractly, we have
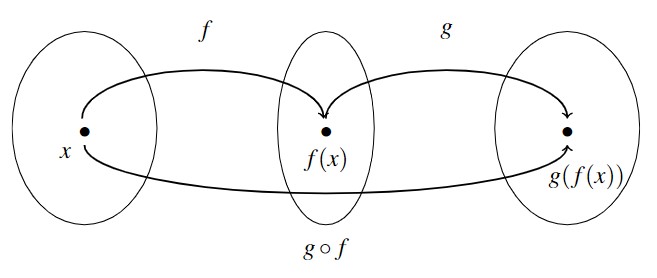
In the expression ![]() , the function
, the function ![]() is often called the `inside’ function while
is often called the `inside’ function while ![]() is often called the `outside’ function. When evaluating composite function values we present two methods in the example below: the `inside out’ and `outside in’ methods.
is often called the `outside’ function. When evaluating composite function values we present two methods in the example below: the `inside out’ and `outside in’ methods.
Example 1.5.3
Example 1.5.3.1
Let ![]() ,
, ![]() , and
, and ![]() .
.
Compute the indicated function value:
![]()
Solution:
Compute ![]() .
.
Using Definition 1.14, ![]() .
.
To start ![]() .
.
Then ![]() , so we have
, so we have
![Rendered by QuickLaTeX.com \[\begin{array}{rcl} (g \circ f)(1) &=& g(f(1)) \\ &=& g(-3) \\ &=& 2. \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-996079e0ffb06cb5eebb17990e168daa_l3.png)
Example 1.5.3.2
Let ![]() ,
, ![]() , and
, and ![]() .
.
Compute the indicated function value:
![]()
Solution:
Compute ![]() .
.
By definition, ![]() .
.
We find ![]() , and
, and
![]() , so
, so
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} (f \circ g)(1) &=& f(g(1)) \\ &=& f(0) \\ &=& 0. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-0e5ca893e7b9df9e9e9626b99981f6ee_l3.png)
Comparing this with our answer to the last problem, we see that ![]() which tells us function composition is not commutative,[5]
which tells us function composition is not commutative,[5]
Example 1.5.3.3
Let ![]() ,
, ![]() , and
, and ![]() .
.
Compute the indicated function value:
![]()
Solution:
Compute ![]() .
.
We note ![]() , and thus we `iterate’ the process
, and thus we `iterate’ the process ![]() : that is, we apply the process
: that is, we apply the process ![]() to
to ![]() , then apply the process
, then apply the process ![]() again.
again.
We find ![]() , and
, and
![]() , so
, so
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} (g \circ g)(6) &=& g(g(6)) \\ &=& g(-1) \\ &=& 2-\sqrt{2}. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5fcf7389c2a2b3878cdf431006d5d61e_l3.png)
Example 1.5.3.4
Let ![]() ,
, ![]() , and
, and ![]() .
.
Determine and simplify the indicated composite functions. State the domain of each.
![]()
Solution:
Determine and simplify ![]() .
.
By definition, ![]() . We now illustrate two ways to approach this problem.
. We now illustrate two ways to approach this problem.
- inside out: We substitute
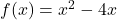 in for
in for  in the expression
in the expression 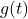 and get
and get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} (g \circ f)(x) &=& g(f(x)) \\ &=& g\left(x^2-4x\right) \\ &=& 2 - \sqrt{\left(x^2-4x\right)+3} \\ &=& 2 - \sqrt{x^2-4x+3} \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d1b3624d6336e7a71845d5e85301f728_l3.png)
Hence,
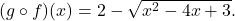
- outside in: We use the formula for
 first to get
first to get
![Rendered by QuickLaTeX.com \[\begin{array}{rcl} (g \circ f)(x) &=& g(f(x)) \\ &=& 2 - \sqrt{f(x)+3} \\ &=& 2 - \sqrt{\left(x^2-4x\right)+3} \\ &=& 2 - \sqrt{x^2-4x+3} \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-282b9d233236718b5b28bad1cd5ad90b_l3.png)
We get the same answer as before,
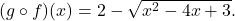
To find the domain of ![]() , we need to find the elements in the domain of
, we need to find the elements in the domain of ![]() whose outputs
whose outputs ![]() are in the domain of
are in the domain of ![]() .
.
To find the domain of ![]() , we need to find the elements in the domain of
, we need to find the elements in the domain of ![]() whose outputs
whose outputs ![]() are in the domain of
are in the domain of ![]() .
.
The domain of ![]() is all real numbers, allowing us to focus on finding the range elements compatible with
is all real numbers, allowing us to focus on finding the range elements compatible with ![]() . Owing to the presence of the square root in the formula
. Owing to the presence of the square root in the formula ![]() we require
we require ![]() .
.
Hence, we need ![]() or
or ![]() . To solve this inequality we rewrite as
. To solve this inequality we rewrite as ![]() and use a sign diagram. Letting
and use a sign diagram. Letting ![]() , we find the zeros of
, we find the zeros of ![]() to be
to be ![]() and
and ![]() and obtain
and obtain
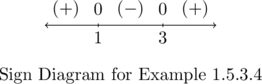
Our solution to ![]() , and hence the domain of
, and hence the domain of ![]() , is
, is ![]() .
.
Example 1.5.3.5
Let ![]() ,
, ![]() , and
, and ![]() .
.
Determine and simplify the indicated composite functions. State the domain of each.
![]()
Solution:
Determine and simplify ![]() .
.
To find ![]() , we find
, we find ![]() .
.
- inside out: We substitute the expression
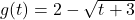 in for
in for  in the formula
in the formula  and get
and get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} (f \circ g)(t) & = & f(g(t)) \\ &=& f\left(2-\sqrt{t+3}\right) \\ [2pt] & = & \left(2-\sqrt{t+3}\right)^2 - 4\left(2-\sqrt{t+3}\right) \\[2pt] & = & 4 - 4\sqrt{t+3} + \left(\sqrt{t+3}\right)^2 - 8 + 4 \sqrt{t+3} \\ [2pt] & = & 4 + t+3 - 8 \\ & = & t-1 \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-10ab2edc6df6193d5b704959d3e93893_l3.png)
- outside in: We use the formula for
 first to get
first to get
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} (f \circ g)(t) & = & f(g(t)) & \\ &=& \left(g(t)\right)^2 - 4\left(g(t)\right) & \\ [2pt] & = & \left(2-\sqrt{t+3}\right)^2 - 4\left(2-\sqrt{t+3}\right) & \\[2pt] & = & t-1 & \text{same algebra as before} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-48019bc2d828e23446d8a6bfb8526aa1_l3.png)
Thus we get ![]() .
.
To find the domain of ![]() , we look for the elements
, we look for the elements ![]() in the domain of
in the domain of ![]() whose outputs,
whose outputs, ![]() are in the domain of
are in the domain of ![]() . As mentioned previously, the domain of
. As mentioned previously, the domain of ![]() is limited by the presence of the square root to
is limited by the presence of the square root to ![]() , while the domain of
, while the domain of ![]() is all real numbers.
is all real numbers.
Hence, the domain of ![]() is restricted only by the domain of
is restricted only by the domain of ![]() and is
and is ![]() or, using interval notation,
or, using interval notation, ![]() .
.
Note that as with Example 1.5.1 of this section, had we used the simplified formula for ![]() to determine domain, we would have arrived at the incorrect answer.
to determine domain, we would have arrived at the incorrect answer.
Example 1.5.3.6
Let ![]() ,
, ![]() , and
, and ![]() .
.
Determine and simplify the indicated composite functions. State the domain of each.
![]()
Solution:
Determine and simplify ![]() .
.
To find ![]() , we compute
, we compute ![]() .
.
- inside out: We substitute
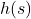 in for
in for  in the expression
in the expression 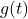 to get
to get
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} (g \circ h)(s) & = & g(h(s)) & \\ &=& g\left(\dfrac{2s}{s+1}\right) & \\ [12pt] & = & 2 - \sqrt{\left(\dfrac{2s}{s+1}\right)+3} & \\[12pt] & = & 2 - \sqrt{\dfrac{2s}{s+1} + \dfrac{3(s+1)}{s+1}} & \text{get common denominators}\\ [12pt] & = & 2 - \sqrt{\dfrac{5s+3}{s+1}} & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a040e1d45a7bf67f1410500b4ea73040_l3.png)
- outside in: We use the formula for
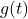 first to get
first to get
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} (g \circ h)(s) & = & g(h(s)) & \\ &=& 2 - \sqrt{h(s)+3}& \\ [2pt] & = & 2 - \sqrt{\left(\dfrac{2s}{s+1}\right)+3} & \\[12pt] & = & 2 - \sqrt{\dfrac{5s+3}{s+1}} & \text{get common denominators as before}\\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-414c5929e2181c5825707d659557473c_l3.png)
To find the domain of ![]() , we need the elements in the domain of
, we need the elements in the domain of ![]() so that
so that ![]() is in the domain of
is in the domain of ![]() .
.
Owing to the ![]() in the denominator of the expression
in the denominator of the expression ![]() , we require
, we require ![]() . Once again, because of the square root in
. Once again, because of the square root in ![]() , we need
, we need ![]() or, in this case
or, in this case ![]() . We rearrange this inequality:
. We rearrange this inequality:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{2s}{s+1} & \geq & -3 & \\ [10pt] \dfrac{2s}{s+1} +3 & \geq & 0 & \\ [10pt] \dfrac{5s+3}{s+1} & \geq & 0 & \text{get common denominators as before} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d3bada617523dcb477e8d52038cc79ed_l3.png)
Defining ![]() , we see
, we see ![]() is undefined at
is undefined at ![]() (a carry over from the domain restriction of
(a carry over from the domain restriction of ![]() ) and
) and ![]() at
at ![]() . Our sign diagram is
. Our sign diagram is
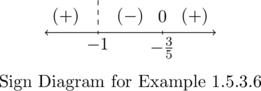
hence our domain is ![]() .
.
Example 1.5.3.7
Let ![]() ,
, ![]() , and
, and ![]() .
.
Determine and simplify the indicated composite functions. State the domain of each.
![]()
Solution:
Determine and simplify ![]() .
.
We find ![]() by finding
by finding ![]() .
.
- inside out: We substitute the expression
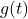 for
for  in the formula
in the formula 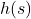
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} (h \circ g)(t) & = & h(g(t)) \\ &=& h\left(2-\sqrt{t+3}\right)\\[2pt] & = & \dfrac{2 \left(2-\sqrt{t+3} \right)}{\left(2-\sqrt{t+3}\right)+1} \\[12pt] & = & \dfrac{4-2\sqrt{t+3}}{3-\sqrt{t+3}}\\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f9936969ed7a3488eb108910a87704e0_l3.png)
- outside in: We use the formula for
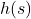 first to get
first to get
![Rendered by QuickLaTeX.com \[\begin{array}{rcl} (h \circ g)(t) & = & h(g(t)) \\ &=& \dfrac{2 \left(g(t)\right)}{\left( g(t)\right) + 1}\\ [12pt] & = & \dfrac{2 \left(2-\sqrt{t+3} \right)}{\left(2-\sqrt{t+3}\right)+1}\\[12pt] & = & \dfrac{4-2\sqrt{t+3}}{3-\sqrt{t+3}} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-1192e1af719252abd3ee559574ccf4f9_l3.png)
To find the domain of ![]() , we need the elements of the domain of
, we need the elements of the domain of ![]() so that
so that ![]() is in the domain of
is in the domain of ![]() . As we’ve seen already, for
. As we’ve seen already, for ![]() to be in the domain of
to be in the domain of ![]() ,
, ![]() . For
. For ![]() to be in the domain of
to be in the domain of ![]() ,
, ![]() , so we require
, so we require ![]() .
.
Hence, we solve ![]() with the intent of excluding these solutions. Isolating the radical expression gives
with the intent of excluding these solutions. Isolating the radical expression gives ![]() or
or ![]() . Sure enough, we check
. Sure enough, we check ![]() , so we exclude
, so we exclude ![]() from the domain of
from the domain of ![]() .
.
Our final answer is ![]() .
.
Example 1.5.3.8
Let ![]() ,
, ![]() , and
, and ![]() .
.
Determine and simplify the indicated composite functions. State the domain of each.
![]()
Solution:
Determine and simplify ![]() .
.
To find ![]() we find
we find ![]() :
:
- inside out: We substitute the expression
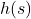 for
for  in the expression
in the expression 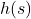 into
into  to get
to get
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} (h \circ h)(s) & = & h(h(s)) & \\[8pt] &=& h\left(\dfrac{2s}{s+1}\right) & \\ [15pt] &=& \dfrac{2\left(\dfrac{2s}{s+1}\right)}{\left(\dfrac{2s}{s+1}\right)+1} & \\ [25pt] & = & \dfrac{\dfrac{4s}{s+1}}{\dfrac{2s}{s+1}+1} \cdot \dfrac{(s+1)}{(s+1)} & \\ [25pt] & = & \dfrac{\dfrac{4s}{s+1} \cdot (s+1)}{\left(\dfrac{2s}{s+1}\right)\cdot(s+1)+1\cdot(s+1)} & \\ [25pt] & = & \dfrac{\dfrac{4s}{\cancelto{1}{(s+1})} \cdot \cancel{(s+1)}}{\dfrac{2s}{\cancelto{1}{(s+1)}}\cdot\cancel{(s+1)}+s+1} & \\ [25pt] & = & \dfrac{4s}{3s+1} & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d98d89693bad0f6bdb43138ec4f5b5e5_l3.png)
- outside in: This approach yields
![Rendered by QuickLaTeX.com \[\begin{array}{rclr} (h \circ h)(s) & = & h(h(s)) & \\[8pt] &=& \dfrac{2 (h(s))}{h(s) + 1} & \\ [.25in] & = & \dfrac{2\left(\dfrac{2s}{s+1}\right)}{\left(\dfrac{2s}{s+1}\right)+1} & \\[.35in] & = & \dfrac{4s}{3s+1} & \text{same algebra as before}\\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-8d735e795a990071ce490a0ba0058838_l3.png)
To find the domain of ![]() , we need to find the elements in the domain of
, we need to find the elements in the domain of ![]() so that the outputs,
so that the outputs, ![]() are also in the domain of
are also in the domain of ![]() .
.
The only domain restriction for ![]() comes from the denominator:
comes from the denominator: ![]() , so in addition to this, we also need
, so in addition to this, we also need ![]() . To this end, we solve
. To this end, we solve ![]() and exclude the answers. Solving
and exclude the answers. Solving ![]() gives
gives ![]() .
.
The domain of ![]() is
is ![]() .
.
Example 1.5.3.9
Let ![]() ,
, ![]() , and
, and ![]() .
.
Determine and simplify the indicated composite functions. State the domain of each.
![]()
Solution:
Determine and simplify ![]() ..
..
The expression ![]() indicates that we first find the composite,
indicates that we first find the composite, ![]() and then compose the function
and then compose the function ![]() with the result.
with the result.
We know from number 4 that ![]() with domain
with domain ![]() . We now proceed as usual.
. We now proceed as usual.
- inside out: We substitute the expression
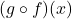 for
for  in the expression
in the expression 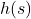 first to get
first to get
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} (h \circ (g \circ f))(x) & = & h((g \circ f)(x)) & \\ &=& h\left(2 - \sqrt{x^2-4x+3}\right) & \\ [5pt] & = & \dfrac{2 \left(2 - \sqrt{x^2-4x+3}\right)}{\left(2 - \sqrt{x^2-4x+3}\right)+1} & \\ [20pt] & = & \dfrac{4 - 2\sqrt{x^2-4x+3}}{3 - \sqrt{x^2-4x+3}} & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-cc72b32cdff5021bc560bbdb977f4e34_l3.png)
- outside in: We use the formula for
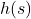 first to get
first to get
![Rendered by QuickLaTeX.com \[\begin{array}{rclr} (h \circ (g \circ f))(x) & = & h((g \circ f)(x)) & \\ &=& \dfrac{2 \left( (g \circ f)(x)\right)}{ \left( (g \circ f)(x)\right) + 1} & \\ [15pt] & = & \dfrac{2 \left(2 - \sqrt{x^2-4x+3}\right)}{\left(2 - \sqrt{x^2-4x+3}\right)+1} & \\ [20pt] & = & \dfrac{4 - 2\sqrt{x^2-4x+3}}{3 - \sqrt{x^2-4x+3}} & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d1ba16850faab9005a4b339dd1941c6f_l3.png)
To find the domain of ![]() , we need the domain elements of
, we need the domain elements of ![]() ,
, ![]() , so that
, so that ![]() is in the domain of
is in the domain of ![]() .
.
As we’ve seen several times already, the only domain restriction for ![]() is
is ![]() , so we set
, so we set ![]() and exclude the solutions. We get
and exclude the solutions. We get ![]() , and, after squaring both sides, we have
, and, after squaring both sides, we have ![]() . We solve
. We solve ![]() using the quadratic formula and obtain
using the quadratic formula and obtain ![]() . The reader is encouraged to check that both of these numbers satisfy the original equation,
. The reader is encouraged to check that both of these numbers satisfy the original equation, ![]() and also belong to the domain of
and also belong to the domain of ![]() ,
, ![]() , and so must be excluded from our final answer.[6]
, and so must be excluded from our final answer.[6]
Our final domain for ![]() is
is ![]() .
.
Example 1.5.3.10
Let ![]() ,
, ![]() , and
, and ![]() .
.
Determine and simplify the indicated composite functions. State the domain of each.
![]()
Solution:
Determine and simplify ![]() .
.
The expression ![]() indicates that we first find the composite
indicates that we first find the composite ![]() and then compose that with
and then compose that with ![]() . From number 7, we have
. From number 7, we have
![]()
with domain ![]() .
.
We know from number 4 that ![]() with domain
with domain ![]() . We now proceed as usual.
. We now proceed as usual.
- inside out: We substitute the expression
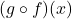 for
for  in the expression
in the expression 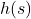 first to get
first to get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} ((h \circ g) \circ f)(x) & = & (h \circ g)(f(x)) \\ &=& (h \circ g)\left(x^2-4x\right) \\ [2pt] & = & \dfrac{4-2\sqrt{\left(x^2-4x\right)+3}}{3-\sqrt{\left(x^2-4x\right)+3}} \\ [20pt] & = & \dfrac{4 - 2\sqrt{x^2-4x+3}}{3 - \sqrt{x^2-4x+3}} \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-92fa43964c9dfcd2cd5df3748e323ee0_l3.png)
- outside in: We use the formula for
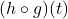 first to get
first to get
![Rendered by QuickLaTeX.com \[\begin{array}{rcl} ((h \circ g) \circ f)(x) & = & (h \circ g)(f(x)) \\ &=& \dfrac{4-2\sqrt{(f(x))+3}}{3-\sqrt{f(x))+3}} \\ [20pt] & = & \dfrac{4 - 2\sqrt{\left(x^2-4x\right)+3}}{3 - \sqrt{\left(x^2-4x\right)+3}} \\[20pt] & = & \dfrac{4 - 2\sqrt{x^2-4x+3}}{3 - \sqrt{x^2-4x+3}} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-250a3b68148c52ed18111ff90733c57f_l3.png)
The domain of ![]() is all real numbers, thus the challenge here in computing the domain of
is all real numbers, thus the challenge here in computing the domain of ![]() is to determine the values
is to determine the values ![]() which are in the domain of
which are in the domain of ![]() ,
, ![]() .
.
At first glance, it appears as if we have two (or three!) inequalities to solve: ![]() and
and ![]() . Alternatively, we could solve
. Alternatively, we could solve ![]() and exclude the solutions to
and exclude the solutions to ![]() which is not only easier from a procedural point of view, but also easier because we’ve already done both calculations. In number 4, we solved
which is not only easier from a procedural point of view, but also easier because we’ve already done both calculations. In number 4, we solved ![]() and obtained the solution
and obtained the solution ![]() and in number 9, we solved
and in number 9, we solved ![]() and obtained
and obtained ![]() .
.
As previously mentioned, it should be clear from Example 1.5.3 that, in general, ![]() , in other words, function composition is not commutative. However, numbers 9 and 10 demonstrate the associative property of function composition. That is, when composing three (or more) functions, as long as we keep the order the same, it doesn’t matter which two functions we compose first. We summarize the important properties of function composition in the theorem below.
, in other words, function composition is not commutative. However, numbers 9 and 10 demonstrate the associative property of function composition. That is, when composing three (or more) functions, as long as we keep the order the same, it doesn’t matter which two functions we compose first. We summarize the important properties of function composition in the theorem below.
Theorem 1.6: Properties of Function Composition
Suppose ![]() ,
, ![]() , and
, and ![]() are functions
are functions
- Associative Law of Composition:
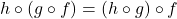 , provided the composite functions are defined.
, provided the composite functions are defined. - Composition Identity: The function
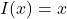 satisfies:
satisfies: 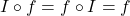 for all functions,
for all functions,  .
.
By repeated applications of Definition 1.14, we find ![]() . Similarly,
. Similarly, ![]() . This establishes that the formulas for the two functions are the same. We leave it to the reader to think about why the domains of these two functions are identical, too. These two facts establish the equality
. This establishes that the formulas for the two functions are the same. We leave it to the reader to think about why the domains of these two functions are identical, too. These two facts establish the equality ![]() . A consequence of the associativity of function composition is that there is no need for parentheses when we write
. A consequence of the associativity of function composition is that there is no need for parentheses when we write ![]() . The second property can also be verified using Definition 1.14. Recall that the function
. The second property can also be verified using Definition 1.14. Recall that the function ![]() is called the identity function and was introduced in Exercise 76 in Section 1.3. If we compose the function
is called the identity function and was introduced in Exercise 76 in Section 1.3. If we compose the function ![]() with a function
with a function ![]() , then we have
, then we have ![]() , and a similar computation shows
, and a similar computation shows ![]() . This establishes that we have an identity for function composition much in the same way the function
. This establishes that we have an identity for function composition much in the same way the function ![]() is an identity for function multiplication.
is an identity for function multiplication.
As we know, not all functions are described by formulas, and, moreover, not all functions are described by just one formula. The next example applies the concept of function composition to functions represented in various and sundry ways.
Example 1.5.4
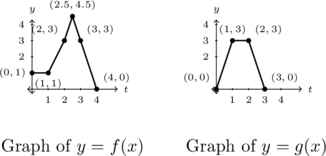
Example 1.5.4.1a
Consider the following functions:
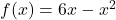
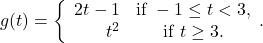
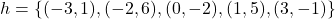
 whose graph is given below:
whose graph is given below:

Compute and simplify the following function values:
![]()
Solution:
Compute and simplify ![]() .
.
To find ![]() , we first find
, we first find ![]() .
.
Considering ![]() , we use the rule
, we use the rule ![]() so
so ![]() .
.
Hence, ![]() .
.
Example 1.5.4.1b
Consider the following functions:
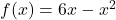
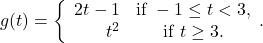
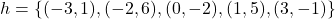
 whose graph is given below:
whose graph is given below:

Compute and simplify the following function values:
![]()
Solution:
Compute and simplify ![]() .
.
As ![]() , we first need
, we first need ![]() .
.
Given ![]() , we use the rule
, we use the rule ![]() and find
and find ![]() .
.
Next, we need ![]() . As
. As ![]() , we have that
, we have that ![]() .
.
Putting this all together, we find ![]() .
.
Example 1.5.4.1c
Consider the following functions:
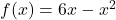
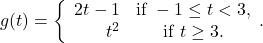
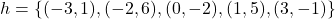
 whose graph is given below:
whose graph is given below:

Compute and simplify the following function values:
![]()
Solution:
Compute and simplify ![]() .
.
To find ![]() , we first need
, we first need ![]() .
.
We see the point ![]() is on the graph of
is on the graph of ![]() , so
, so ![]() .
.
Next, we see ![]() , so
, so ![]() .
.
Hence, ![]() .
.
Example 1.5.4.1d
Consider the following functions:
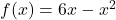
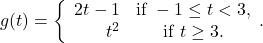
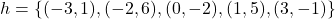
 whose graph is given below:
whose graph is given below:

Compute and simplify the following function values:
![]()
Solution:
Compute and simplify ![]() .
.
To find ![]() , we infer from the graph of
, we infer from the graph of ![]() that it contains the point
that it contains the point ![]() , so
, so ![]() .
.
Then ![]() .
.
Thus we have ![]() .
.
Example 1.5.4.2
Consider the following functions:
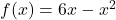
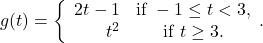
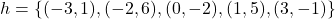
 whose graph is given below:
whose graph is given below:

Determine and simplify a formula for ![]() .
.
Solution:
Determine and simplify a formula for ![]() .
.
To determine a formula for ![]() , we substitute
, we substitute ![]() in for
in for ![]() in the formula for
in the formula for ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} (g \circ f)(x) &=& g(f(x)) \\[3pt] &=& g(6x-x^2) \\[12pt] &=& \left\{ \begin{array}{rc} 2(6x-x^2) -1 & \text{if } -1 \leq 6x-x^2 < 3, \\[8pt] (6x-x^2)^2 & \text{if }6x-x^2 \geq 3. \\ \end{array} \right. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c585f1ac734a714cc7491a07adec1534_l3.png)
Simplifying each expression, we get ![]() for the first piece and
for the first piece and ![]() for the second piece.
for the second piece.
The real challenge comes in solving the inequalities ![]() and
and ![]() . While we could solve each individually using a sign diagram, a graphical approach works best here. We graph the parabola
. While we could solve each individually using a sign diagram, a graphical approach works best here. We graph the parabola ![]() , identifying the vertex is
, identifying the vertex is ![]() with intercepts
with intercepts ![]() and
and ![]() along with the horizontal lines
along with the horizontal lines ![]() and
and ![]() below.
below.
We determine the intersection points by solving ![]() and
and ![]() .
.
Using the quadratic formula, we find the solutions to each equation are ![]() and
and ![]() , respectively.
, respectively.
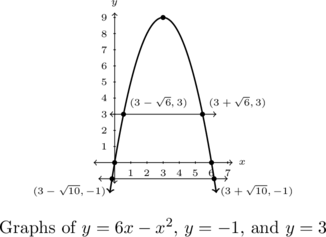
From the graph, we see the parabola ![]() is between the lines
is between the lines ![]() and
and ![]() from
from ![]() to
to ![]() and again from
and again from ![]() to
to ![]() . Hence the solution to
. Hence the solution to ![]() is
is ![]() .
.
We also note ![]() is above the line
is above the line ![]() for all
for all ![]() between
between ![]() and
and ![]() . Hence, the solution to
. Hence, the solution to ![]() is
is ![]() .
.
Hence,
![Rendered by QuickLaTeX.com \[ (g \circ f)(x) = \left\{ \begin{array}{rc} -2x^2+12x-1 & \text{if } x \in [3- \sqrt{10}, 3 - \sqrt{6}) \cup (3+\sqrt{6}, 3+\sqrt{10}], \\[8pt] x^4 - 12x^3 +36x^2 & \text{if } x \in [3-\sqrt{6}, 3+\sqrt{6}]. \\ \end{array} \right.}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9d045b1661d9fbe6e67bd9fb658e0c1d_l3.png)
Example 1.5.4.3
Consider the following functions:
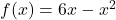
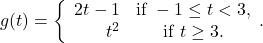
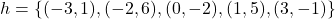
 whose graph is given below:
whose graph is given below:

Write ![]() as a set of ordered pairs.
as a set of ordered pairs.
Solution:
Write ![]() as a set of ordered pairs.
as a set of ordered pairs.
Last but not least, we are tasked with representing ![]() as a set of ordered pairs.
as a set of ordered pairs.
![]() is described by the discrete set of points,
is described by the discrete set of points, ![]() , so we will find
, so we will find ![]() point by point. We keep the graph of
point by point. We keep the graph of ![]() handy and construct the table below to help us organize our work.
handy and construct the table below to help us organize our work.
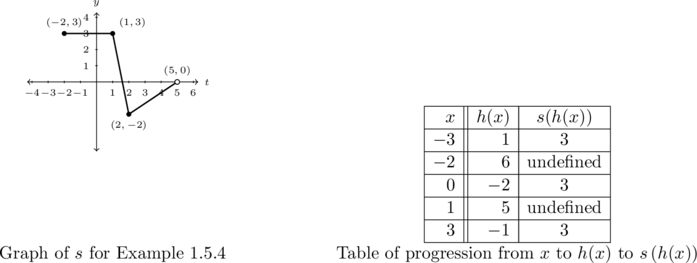
Neither ![]() nor
nor ![]() are in the domain of
are in the domain of ![]() , therefore
, therefore ![]() and
and ![]() are not in the domain of
are not in the domain of ![]() .
.
Hence, we get ![]() .
.
A useful skill in Calculus is to be able to take a complicated function and break it down into a composition of easier functions which our last example illustrates. As with Example 1.52, we want to avoid trivial decompositions, which, when it comes to function composition, are those involving the identity function ![]() as described in Theorem 1.6.
as described in Theorem 1.6.
Example 1.5.5
Example 1.5.5.1a
Write each of the following functions as a composition of two or more (non-identity) functions. Check your answer by performing the function composition.
![]()
Solution:
There are many approaches to this kind of problem, and we showcase a different methodology in each of the solutions below.
Write ![]() as a composition of two or more functions.
as a composition of two or more functions.
Our goal is to express the function ![]() as
as ![]() for functions
for functions ![]() and
and ![]() .
.
From Definition 1.14, we know ![]() , and we can think of
, and we can think of ![]() as being the `inside’ function and
as being the `inside’ function and ![]() as being the `outside’ function.
as being the `outside’ function.
Looking at ![]() from an `inside versus outside’ perspective, we can think of
from an `inside versus outside’ perspective, we can think of ![]() being inside the absolute value symbols. Taking this cue, we define
being inside the absolute value symbols. Taking this cue, we define ![]() .
.
At this point, we have ![]() . What is the outside function? The function which takes the absolute value of its input,
. What is the outside function? The function which takes the absolute value of its input, ![]() .
.
Sure enough, this checks:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} (g \circ f)(x) &=& g(f(x)) \\ &=& |f(x)| \\ &=& |3x-1| \\ &=& F(x). \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5f3916fa903a96fa0578bfb5aff59e27_l3.png)
Example 1.5.5.1b
Write each of the following functions as a composition of two or more (non-identity) functions. Check your answer by performing the function composition.
![]()
Solution:
There are many approaches to this kind of problem, and we showcase a different methodology in each of the solutions below.
Write ![]() as a composition of two or more functions.
as a composition of two or more functions.
We attack deconstructing ![]() from an operational approach.
from an operational approach.
Given an input ![]() , the first step is to square
, the first step is to square ![]() , then add
, then add ![]() , then divide the result into
, then divide the result into ![]() . We will assign each of these steps a function so as to write
. We will assign each of these steps a function so as to write ![]() as a composite of three functions:
as a composite of three functions: ![]() ,
, ![]() and
and ![]() .
.
Our first function, ![]() , is the function that squares its input,
, is the function that squares its input, ![]() .
.
The next function is the function that adds ![]() to its input,
to its input, ![]() .
.
Our last function takes its input and divides it into ![]() ,
, ![]() .
.
The claim is that ![]() which checks:
which checks:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} (h \circ g \circ f)(t) &=& h(g(f(t))) \\[4pt] &=& h(g\left(t^2\right)) \\[4pt] &=& h\left(t^2+1\right) \\[4pt] &=& \frac{2}{t^2+1} \\[4pt] &=& G(x). \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-35b5ccf70297c78d723168c06f113b46_l3.png)
Example 1.5.5.1c
Write each of the following functions as a composition of two or more (non-identity) functions. Check your answer by performing the function composition.
![]()
Solution:
There are many approaches to this kind of problem, and we showcase a different methodology in each of the solutions below.
Write ![]() as a composition of two or more functions.
as a composition of two or more functions.
If we look ![]() with an eye towards building a complicated function from simpler functions, we see the expression
with an eye towards building a complicated function from simpler functions, we see the expression ![]() is a simple piece of the larger function.
is a simple piece of the larger function.
If we define ![]() , we have
, we have ![]() .
.
If we want to decompose ![]() , then we can glean the formula for
, then we can glean the formula for ![]() by looking at what is being done to
by looking at what is being done to ![]() .
.
We take ![]() , and check below:
, and check below:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} (g \circ f)(s) &=& g(f(s)) \\[4pt] &=& \frac{f(s)+1}{f(s)-1} \\[4pt] &=& \frac{\sqrt{s}+1}{\sqrt{s}-1} \\[4pt] &=& H(s). \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-eaa9fff397b47fe0fd478ead4434d079_l3.png)
Example 1.5.5.2
For ![]() , find functions
, find functions ![]() ,
, ![]() , and
, and ![]() to decompose
to decompose ![]() nontrivially as
nontrivially as ![]() .
.
Solution:
For ![]() , find functions
, find functions ![]() ,
, ![]() , and
, and ![]() to decompose
to decompose ![]() nontrivially as
nontrivially as ![]() .
.
To write ![]() means
means
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} F(x) &=& \sqrt{\dfrac{2x-1}{x^2+4}} \\[8pt] &=& \left( f \circ \left(\dfrac{g}{h} \right) \right)(x) \\[8pt] &=& f \left( \left(\dfrac{g}{h} \right)(x) \right) \\[8pt] &=& f \left( \dfrac{g(x)}{h(x)} \right). \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-79bca42bb69dacaf1eee06220be038ed_l3.png)
Working from the inside out, we have a rational expression with numerator ![]() and denominator
and denominator ![]() .
.
Looking at the formula for ![]() , one choice is
, one choice is ![]() and
and ![]() . Making these identifications, we have
. Making these identifications, we have
![Rendered by QuickLaTeX.com \[ F(x) = \sqrt{\dfrac{2x-1}{x^2+4}} = \sqrt{\dfrac{g(x)}{h(x)}}.\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-315ccbea5d583e7b01a97fab80d2f321_l3.png)
![]() takes the square root of
takes the square root of ![]() , which tells us that our last function,
, which tells us that our last function, ![]() , is the function that takes the square root of its input, i.e.,
, is the function that takes the square root of its input, i.e., ![]() .
.
We leave it to the reader to check that, indeed, ![]() .
.
We close this section of a real-world application of function composition.
Example 1.5.6
Example 1.5.6
The surface area of a sphere is a function of its radius ![]() and is given by the formula
and is given by the formula ![]() . Suppose the sphere is being inflated so that the radius of the sphere is increasing according to the formula
. Suppose the sphere is being inflated so that the radius of the sphere is increasing according to the formula ![]() , where
, where ![]() is measured in seconds,
is measured in seconds, ![]() , and
, and ![]() is measured in inches. Find and interpret
is measured in inches. Find and interpret ![]() .
.
Solution:
If we look at the functions ![]() and
and ![]() individually, we see the former gives the surface area of a sphere of a given radius while the latter gives the radius at a given time.
individually, we see the former gives the surface area of a sphere of a given radius while the latter gives the radius at a given time.
So, given a specific time, ![]() , we could find the radius at that time,
, we could find the radius at that time, ![]() and feed that into
and feed that into ![]() to compute the surface area at that time.
to compute the surface area at that time.
From this we see that the surface area ![]() is ultimately a function of time
is ultimately a function of time ![]() and we conclude
and we conclude
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} (S \circ r)(t) &=& S(r(t)) \\ &=& 4 \pi (r(t))^2 \\ &=& 4 \pi \left(3t^2\right)^2 \\ &=& 36 \pi t^{4}. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5f051e7c78581bb768cc0ce9f9fee00f_l3.png)
This formula allows us to compute the surface area directly given the time without going through the `intermediary variable’ ![]() .
.
1.5.3 Section Exercises
In Exercises 1 – 10, use the pair of functions ![]() and
and ![]() to find the following values if they exist.
to find the following values if they exist.
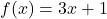 and
and 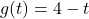
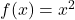 and
and 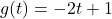
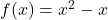 and
and 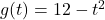
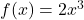 and
and 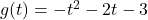
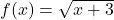 and
and 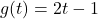
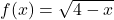 and
and 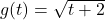
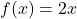 and
and 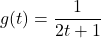
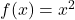 and
and 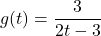
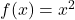 and
and 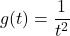
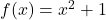 and
and 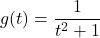
Exercises 11 – 20 refer to the functions ![]() and
and ![]() whose graphs are below.
whose graphs are below.
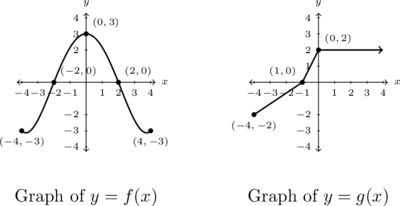
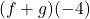
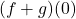
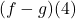
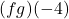
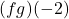
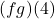
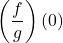
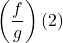
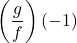
- Compute the domains of
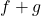 ,
,  ,
, 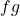 ,
, 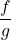 and
and 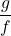 .
.
In Exercises 21 – 32, let ![]() be the function defined by
be the function defined by
![]()
and let ![]() be the function defined by
be the function defined by
![]()
Compute the indicated value if it exists.
In Exercises 33 – 42, use the pair of functions ![]() and
and ![]() to find the domain of the indicated function then find and simplify an expression for it.
to find the domain of the indicated function then find and simplify an expression for it.
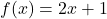 and
and 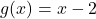
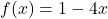 and
and 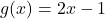
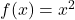 and
and 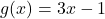
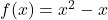 and
and 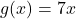
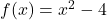 and
and 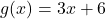
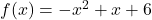 and
and 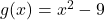
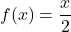 and
and 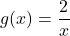
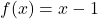 and
and 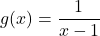
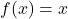 and
and 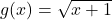
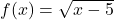 and
and 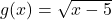
In Exercises 43 – 47, write the given function as a nontrivial decomposition of functions as directed.
- For
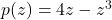 , find functions
, find functions  and
and  so that
so that 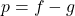 .
. - For
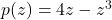 , find functions
, find functions  and
and  so that
so that 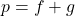 .
. - For
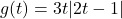 , find functions
, find functions  and
and  so that
so that 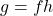 .
. - For
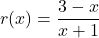 , find functions
, find functions  and
and  so
so 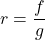 .
. - For
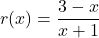 , find functions
, find functions  and
and  so
so 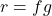 .
. - Can
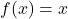 be decomposed as
be decomposed as 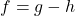 where
where 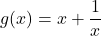 and
and 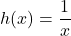 ?
?
In Exercises 49 – 60, use the given pair of functions to find the following values if they exist.
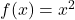 and
and 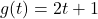
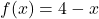 and
and 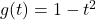
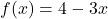 and
and 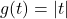
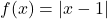 and
and 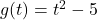
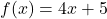 and
and 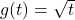
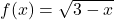 and
and 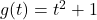
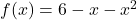 and
and 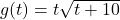
![Rendered by QuickLaTeX.com f(x) = \sqrt[3]{x+1}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-34dc0cf05ce03581ca11f0d69b51fcdf_l3.png) and
and 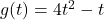
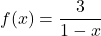 and
and 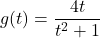
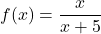 and
and 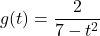
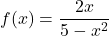 and
and 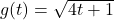
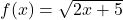 and
and 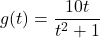
In Exercises 61 – 72, use the given pair of functions to find and simplify expressions for the following functions and state the domain of each using interval notation.
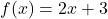 and
and 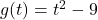
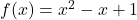 and
and 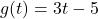
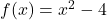 and
and 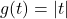
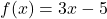 and
and 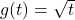
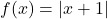 and
and 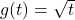
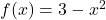 and
and 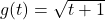
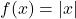 and
and 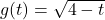
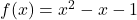 and
and 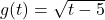
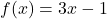 and
and 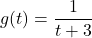
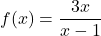 and
and 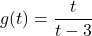
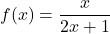 and
and 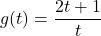
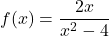 and
and 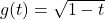
In Exercises 73 – 78, use ![]() ,
, ![]() and
and ![]() to find and simplify expressions for the following functions and state the domain of each using interval notation.
to find and simplify expressions for the following functions and state the domain of each using interval notation.
In Exercises 79 – 91, let ![]() be the function defined by
be the function defined by
![]()
and let ![]() be the function defined by
be the function defined by
![]()
Find the following, if it exists.
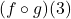
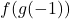
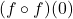
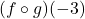
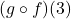
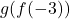
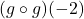
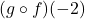
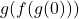
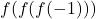
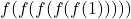
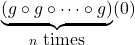
- Find the domain and range of
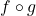 and
and 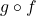 .
.
In Exercises 92 – 98, use the graphs of ![]() and
and ![]() below to find the following if it exists.
below to find the following if it exists.
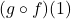
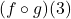
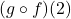
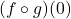
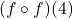
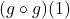
- Find the domain and range of
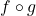 and
and 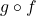 .
.
In Exercises 99 – 108, write the given function as a composition of two or more non-identity functions. (There are several correct answers, so check your answer using function composition.)
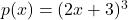
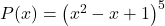
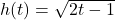
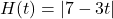
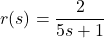
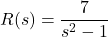
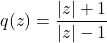
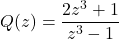
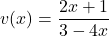
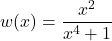
- Write the function
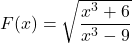 as a composition of three or more non-identity functions.
as a composition of three or more non-identity functions. - Let
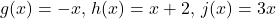 and
and 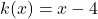 . In what order must these functions be composed with
. In what order must these functions be composed with 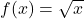 to create
to create 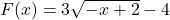 ?
? - What linear functions could be used to transform
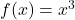 into
into 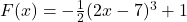 ? What is the proper order of composition?
? What is the proper order of composition? - Let
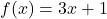 and let
and let 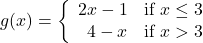 . Find expressions for
. Find expressions for 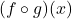 and
and 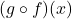 .
. - The volume
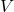 of a cube is a function of its side length
of a cube is a function of its side length  . Let’s assume that
. Let’s assume that 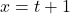 is also a function of time
is also a function of time  , where
, where  is measured in inches and
is measured in inches and  is measured in minutes. Find a formula for
is measured in minutes. Find a formula for 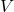 as a function of
as a function of  .
. - Suppose a local vendor charges
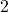 per hot dog and that the number of hot dogs sold per hour
per hot dog and that the number of hot dogs sold per hour  is given by
is given by 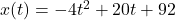 , where
, where  is the number of hours since
is the number of hours since 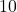 AM,
AM, 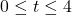 .
.
- Find an expression for the revenue per hour
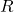 as a function of
as a function of  .
. - Find and simplify
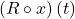 . What does this represent?
. What does this represent? - What is the revenue per hour at noon?
- Find an expression for the revenue per hour
Section 1.5 Exercise Answers can be found in the Appendix … Coming soon
- We could have just as easily called this new function
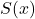 for `sum' of
for `sum' of  and
and  and defined
and defined  by
by 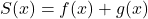 . ↵
. ↵ - see Section 0.4. ↵
- Due to the fact that
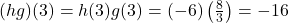 , we can write
, we can write 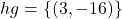 . ↵
. ↵ - Addition is a `binary' operation - meaning it is defined only on two objects at once. Even though we write
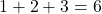 , mentally, we add just two of numbers together at any given time to get our answer: for example,
, mentally, we add just two of numbers together at any given time to get our answer: for example, 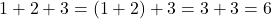 . ↵
. ↵ - That is, in general,
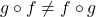 . This shouldn't be too surprising, because, in general, the order of processes matters: adding eggs to a cake batter then baking the cake batter has a much different outcome than baking the cake batter then adding eggs. ↵
. This shouldn't be too surprising, because, in general, the order of processes matters: adding eggs to a cake batter then baking the cake batter has a much different outcome than baking the cake batter then adding eggs. ↵ - We can approximate
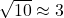 so
so 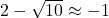 and
and 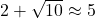 . ↵
. ↵
Given two functions f and g, where the real number x is in the domain of g and the real number g(x) is in the domain of f, f composed with g is defined by replacing all x in the function f with the function g.

