2.1 Quadratic Functions
2.1.1 Graphs of Quadratic Functions
You may recall studying quadratic equations in a previous Algebra course. If not, you may wish to refer to Section 0.5.5 to revisit this topic. In this section, we review those equations in the context of our next family of functions: the quadratic functions.
Definition 2.1
A quadratic function is a function of the form
![]()
where ![]() ,
, ![]() and
and ![]() are real numbers with
are real numbers with ![]() .
.
The domain of a quadratic function is ![]() .
.
As in Definitions 1.9 and 1.10, the independent variable in Definition 2.1 is ![]() while the values
while the values ![]() ,
, ![]() and
and ![]() are parameters. Note that
are parameters. Note that ![]() – otherwise we would have a linear function (see Definition 1.10).
– otherwise we would have a linear function (see Definition 1.10).
The most basic quadratic function is ![]() , the squaring function, whose graph appears below along with a corresponding table of values. Its shape may look familiar from your previous studies in Algebra — it is called a parabola. The point
, the squaring function, whose graph appears below along with a corresponding table of values. Its shape may look familiar from your previous studies in Algebra — it is called a parabola. The point ![]() is called the vertex of the parabola because it is the sole point where the function obtains its extreme value, in this case, a minimum of
is called the vertex of the parabola because it is the sole point where the function obtains its extreme value, in this case, a minimum of ![]() when
when ![]() .
.
Indeed, the range of ![]() appears to be
appears to be ![]() from the graph. We can substantiate this algebraically because for all
from the graph. We can substantiate this algebraically because for all ![]() ,
, ![]() . This tells us that the range of
. This tells us that the range of ![]() is a subset of
is a subset of ![]() . To show that the range of
. To show that the range of ![]() actually equals
actually equals ![]() , we need to show that every real number
, we need to show that every real number ![]() in
in ![]() is in the range of
is in the range of ![]() . That is, for every
. That is, for every ![]() , we have to show
, we have to show ![]() is an output from
is an output from ![]() . In other words, we have to show there is a real number
. In other words, we have to show there is a real number ![]() so that
so that ![]() . Choosing
. Choosing ![]() , we find
, we find ![]() , as required.[1]
, as required.[1]
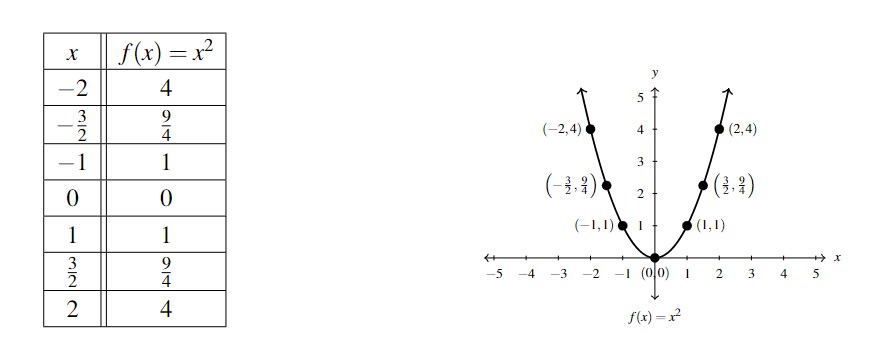
The techniques we used to graph many of the absolute value functions in Section 1.4 can be applied to quadratic functions, too. In fact, knowing the graph of ![]() enables us to graph every quadratic function, but there’s some extra work involved. We start with the following theorem:
enables us to graph every quadratic function, but there’s some extra work involved. We start with the following theorem:
Theorem 2.1
For real numbers ![]() ,
, ![]() and
and ![]() with
with ![]() , the graph of
, the graph of ![]() is a parabola with vertex
is a parabola with vertex ![]() .
.
- If
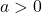 , the graph resembles `
, the graph resembles ` .’
.’ - If
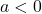 , the graph resembles `
, the graph resembles ` .’
.’
Moreover, the vertical line ![]() is the axis of symmetry of the graph of
is the axis of symmetry of the graph of ![]() .
.
To prove Theorem 2.1 the reader is encouraged to revisit the discussion following the proof of Theorem 1.4, replacing every occurrence of absolute value notation with the squared exponent.[2] Alternatively, the reader can skip ahead and read the statement and proof of Theorem 2.2 in Section 2.2. In the meantime we put Theorem 2.1 to good use in the next example.
Example 2.1.1
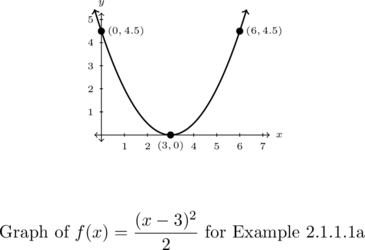
Example 2.1.1.1a
Graph the following functions using Theorem 2.1. Determine the vertex, zeros and axis-intercepts (if any exist). Identify the extrema and then list the intervals over which the function is increasing, decreasing or constant.
![]()
Solution:
Graph ![]() .
.
For ![]() , we identify
, we identify ![]() ,
, ![]() and
and ![]() .
.
Thus the vertex is ![]() and the parabola opens upwards.
and the parabola opens upwards.
The only ![]() -intercept is
-intercept is ![]() .
.
Our ![]() -intercept is
-intercept is ![]() , because
, because ![]() .
.
To help us graph the function, it would be nice to have a third point and we’ll use symmetry to find it. The ![]() -value three units to the left of the vertex is
-value three units to the left of the vertex is ![]() , so the
, so the ![]() -value must be
-value must be ![]() three units to the right of the vertex as well. Hence, we have our third point:
three units to the right of the vertex as well. Hence, we have our third point: ![]() .
.
From the graph, we identify that the range is ![]() and see that
and see that ![]() has the minimum value of
has the minimum value of ![]() at
at ![]() and no maximum.
and no maximum.
Also, ![]() is decreasing on
is decreasing on ![]() and increasing on
and increasing on ![]() .
.
The graph is below.
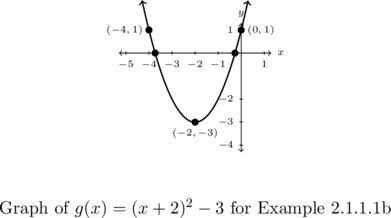
Example 2.1.1.1b
Graph the following functions using Theorem 2.1. Determine the vertex, zeros and axis-intercepts (if any exist). Identify the extrema and then list the intervals over which the function is increasing, decreasing or constant.
![]()
Solution:
Graph ![]() .
.
For ![]() , we identify
, we identify ![]() ,
, ![]() and
and ![]() .
.
This means that the vertex is ![]() and the parabola opens upwards.
and the parabola opens upwards.
Thus we have two ![]() -intercepts. To find them, we set
-intercepts. To find them, we set ![]() and solve. Doing so yields the equation
and solve. Doing so yields the equation ![]() , or
, or ![]() . Extracting square roots gives us the two zeros of
. Extracting square roots gives us the two zeros of ![]() :
: ![]() , or
, or ![]() . Our
. Our ![]() -intercepts are
-intercepts are ![]() and
and ![]() .
.
We find ![]() so our
so our ![]() -intercept is
-intercept is ![]() .
.
Using symmetry, we get ![]() as another point to help us graph.
as another point to help us graph.
The range of ![]() is
is ![]() . The minimum of
. The minimum of ![]() is
is ![]() at
at ![]() , and
, and ![]() has no maximum.
has no maximum.
Moreover, ![]() is decreasing on
is decreasing on ![]() and
and ![]() is increasing on
is increasing on ![]() .
.
The graph is below.
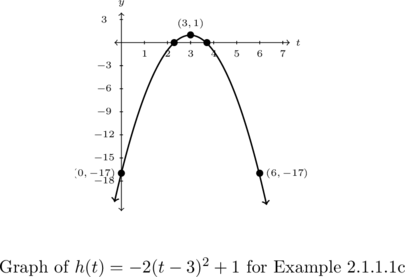
Example 2.1.1.1c
Graph the following functions using Theorem 2.1. Determine the vertex, zeros and axis-intercepts (if any exist). Identify the extrema and then list the intervals over which the function is increasing, decreasing or constant.
![]()
Solution:
Graph ![]() .
.
Given ![]() , we identify
, we identify ![]() ,
, ![]() and
and ![]() .
.
Hence the vertex of the graph is ![]() and the parabola opens downwards.
and the parabola opens downwards.
Solving ![]() gives
gives ![]() . Extracting square roots\footnote{and rationalizing denominators!} gives
. Extracting square roots\footnote{and rationalizing denominators!} gives ![]() , so that when we add
, so that when we add ![]() to each side,[3] we get
to each side,[3] we get ![]() . Hence, our
. Hence, our ![]() -intercepts are
-intercepts are ![]() and
and ![]() .
.
To find the ![]() -intercept, we compute
-intercept, we compute ![]() . Thus the
. Thus the ![]() -intercept is
-intercept is ![]() .
.
Using symmetry, we also know ![]() is on the graph.
is on the graph.
The range of ![]() is
is ![]() . The maximum of
. The maximum of ![]() is
is ![]() at
at ![]() , and
, and ![]() has no minimum.
has no minimum.
Moreover, ![]() is increasing on
is increasing on ![]() and
and ![]() is increasing on
is increasing on ![]() .
.
The graph is below.
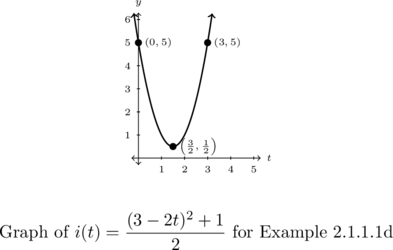
Example 2.1.1.1d
Graph the following functions using Theorem 2.1. Determine the vertex, zeros and axis-intercepts (if any exist). Identify the extrema and then list the intervals over which the function is increasing, decreasing or constant.
![]()
Solution:
Graph ![]() .
.
We have some work ahead of us to put ![]() into a form we can use to exploit Theorem 2.1:
into a form we can use to exploit Theorem 2.1:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} i(t) &=& \dfrac{(3 - 2t)^2 + 1}{2} \\[8pt] & = & \frac{1}{2} (-2t + 3)^2 + \frac{1}{2} \\[8pt] & = & \frac{1}{2} \left[ -2 \left(t - \frac{3}{2}\right) \right]^2 + \frac{1}{2} \\ [8pt] & = & \frac{1}{2} (-2)^2 \left(t - \frac{3}{2}\right)^2 + \frac{1}{2} \\[8pt] & = & 2\left(t - \frac{3}{2}\right)^2 + \frac{1}{2} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-2bed0cb76c47a20c30f61b6feba53ca0_l3.png)
We identify ![]() ,
, ![]() and
and ![]() .
.
Hence our vertex is ![]() and the parabola opens upwards, meaning there are no
and the parabola opens upwards, meaning there are no ![]() -intercepts.
-intercepts.
By computing ![]() , we get
, we get ![]() as the
as the ![]() -intercept.
-intercept.
Using symmetry, this means we also have ![]() on the graph.
on the graph.
The range is ![]() with the minimum of
with the minimum of ![]() ,
, ![]() , occurring when
, occurring when ![]() .
.
Also, ![]() is decreasing on
is decreasing on ![]() and increasing on
and increasing on ![]() .
.
The graph is given next.
Example 2.1.1.2
Use Theorem 2.1 to write a possible formula for ![]() whose graph is given below:
whose graph is given below:
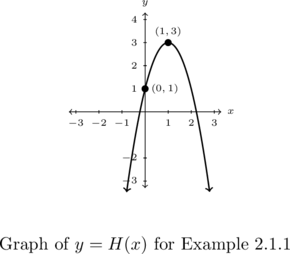
Solution:
Use Theorem 2.1 to write a possible formula for ![]() whose graph is given.
whose graph is given.
We are instructed to use Theorem 2.1, so we know ![]() for some choice of parameters
for some choice of parameters ![]() ,
, ![]() and
and ![]() .
.
The vertex is ![]() so we know
so we know ![]() and
and ![]() , and hence
, and hence ![]() .
.
To determine the value of ![]() , we use the fact that the
, we use the fact that the ![]() -intercept, as labeled, is
-intercept, as labeled, is ![]() . This means
. This means ![]() , or
, or ![]() . This reduces to
. This reduces to ![]() or
or ![]() .
.
Our final answer[4] is ![]() .
.
A few remarks about Example 2.1.1 are in order. First note that none of the functions are in the form of Definition 2.1. However, if we took the time to perform the indicated operations and simplify, we’d determine:
While the ![]() -intercepts of the graphs of the each of the functions are easier to see when the formulas for the functions are written in the form of Definition 2.1, the vertex is not. For this reason, the form of the functions presented in Theorem 2.1 are given a special name.
-intercepts of the graphs of the each of the functions are easier to see when the formulas for the functions are written in the form of Definition 2.1, the vertex is not. For this reason, the form of the functions presented in Theorem 2.1 are given a special name.
Definition 2.2 Standard and General Form of Quadratic Functions
- The general form of the quadratic function
 is
is 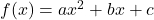 , where
, where  ,
,  and
and  are real numbers with
are real numbers with 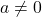 .
. - The standard form of the quadratic function
 is
is 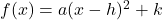 , where
, where  ,
,  and
and 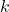 are real numbers with
are real numbers with 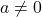 . The standard form is often called the vertex form.
. The standard form is often called the vertex form.
If we proceed as in the remarks following Example 2.1.1, we can convert any quadratic function given to us in standard form and convert to general form by performing the indicated operation and simplifying:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f(x) & = & a(x-h)^2 + k \\ &= & a \left(x^2 -2hx + h^2 \right) + k \\ & = & ax^2 - 2ahx + ah^2 + k \\ & = & a x^2 + (-2ah)x + (ah^2+k). \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e4b387734047ef03892dbf2f28b9f49d_l3.png)
With the identifications ![]() and
and ![]() , we have written
, we have written ![]() in the form
in the form ![]() . Likewise, through a process known as `completing the square’, we can take any quadratic function written in general form and rewrite it in standard form. We briefly review this technique in the following example — for a more thorough review the reader should see Section 0.5.5.
. Likewise, through a process known as `completing the square’, we can take any quadratic function written in general form and rewrite it in standard form. We briefly review this technique in the following example — for a more thorough review the reader should see Section 0.5.5.
Example 2.1.2
Example 2.1.2.1
Graph the following functions. Determine the vertex, zeros and axis-intercepts, if any exist. Identify the extrema and then list the intervals over which the function is increasing, decreasing or constant.
![]()
Solution:
Graph ![]() . Determine the vertex, zeros and axis-intercepts, if any exist. Identify the extrema and then list the intervals over which the function is increasing, decreasing or constant.
. Determine the vertex, zeros and axis-intercepts, if any exist. Identify the extrema and then list the intervals over which the function is increasing, decreasing or constant.
We follow the procedure for completing the square in Section 0.5.5. The only difference here is instead of the quadratic equation being set to ![]() , it is equal to
, it is equal to ![]() . This means when we are finished completing the square, we need to solve for
. This means when we are finished completing the square, we need to solve for ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} f(x) & = & x^2 - 4x+3 & \\ [4pt] f(x) - 3 & = & x^2-4x & \text{Subtract $3$ from both sides.} \\ [4pt] f(x) - 3 + (-2)^2 & = & x^2-4x+(-2)^2 & \text{Add $\left(\frac{1}{2}(-4)\right)^2$ to both sides.} \\ [4pt] f(x) + 1 & = & (x-2)^2 & \text{Factor the perfect square trinomial.} \\ [4pt] f(x) & = & (x-2)^2 - 1 & \text{Solve for $f(x)$.} \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c87f64366a50e587b46aaaa463de5384_l3.png)
The reader is encouraged to start with ![]() , perform the indicated operations and simplify the result to
, perform the indicated operations and simplify the result to ![]() .
.
From the standard form, ![]() , we see that the vertex is
, we see that the vertex is ![]() and that the parabola opens upwards.
and that the parabola opens upwards.
To find the zeros of ![]() , we set
, we set ![]() .
.
We have two equivalent expressions for ![]() so we could use either the general form or standard form. We solve the former and leave it to the reader to solve the latter to see that we get the same results either way. To solve
so we could use either the general form or standard form. We solve the former and leave it to the reader to solve the latter to see that we get the same results either way. To solve ![]() , we factor:
, we factor: ![]() and obtain
and obtain ![]() and
and ![]() . We get two
. We get two ![]() -intercepts,
-intercepts, ![]() and
and ![]() .
.
To find the ![]() -intercept, we need
-intercept, we need ![]() . Again, we could use either form of
. Again, we could use either form of ![]() for this and we choose the general form and find that the
for this and we choose the general form and find that the ![]() -intercept is
-intercept is ![]() .
.
From symmetry, we know the point ![]() is also on the graph.
is also on the graph.
We see that the range of ![]() is
is ![]() with the minimum
with the minimum ![]() at
at ![]() .
.
Finally, ![]() is decreasing on
is decreasing on ![]() and increasing from
and increasing from ![]() .
.
The graph is below.
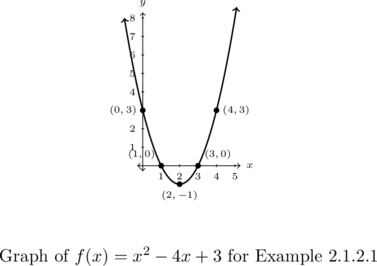
Example 2.1.2.2
Graph the following functions. Determine the vertex, zeros and axis-intercepts, if any exist. Identify the extrema and then list the intervals over which the function is increasing, decreasing or constant.
![]()
Solution:
Graph ![]() . Determine the vertex, zeros and axis-intercepts, if any exist. Identify the extrema and then list the intervals over which the function is increasing, decreasing or constant.
. Determine the vertex, zeros and axis-intercepts, if any exist. Identify the extrema and then list the intervals over which the function is increasing, decreasing or constant.
We first rewrite ![]() as
as ![]() . As with the previous example, once we complete the square, we solve for
. As with the previous example, once we complete the square, we solve for ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} g(t) & = & -2t^2-4t+6 & \\ [6pt] g(t) - 6 & = & -2t^2-4t & \text{Subtract $6$ from both sides.} \\ [6pt] \dfrac{g(t) - 6}{-2} & = & \dfrac{ -2t^2-4t }{-2} & \text{Divide both sides by $-2$.}\\ [10pt] \dfrac{g(t) - 6}{-2} + (1)^2 & = & t^2+2t +(1)^2 & \text{Add $\left( \frac{1}{2} (2) \right)^2$ to both sides.} \\ [10pt] \dfrac{g(t) - 6}{-2} + 1 & = & (t+1)^2 & \text{Factor the prefect square trinomial.} \\ [10pt] \dfrac{g(t) - 6}{-2} & = & (t+1)^2 - 1 & \\ [10pt] g(t) - 6 & = & -2 \left[ (t+1)^2-1 \right] & \\ [6pt] g(t) & = & -2(t+1)^2 + 2 + 6 & \\ [6pt] g(t) & = & -2(t+1)^2+8 \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4f4a3b616a76ad01be199f159e08a820_l3.png)
We can check our answer by expanding ![]() and show that it simplifies to
and show that it simplifies to ![]() .
.
From the standard form, we identify the vertex is ![]() and that the parabola opens downwards.
and that the parabola opens downwards.
Setting ![]() , we factor to get
, we factor to get ![]() so
so ![]() and
and ![]() . Hence, our two
. Hence, our two ![]() -intercepts are
-intercepts are ![]() and
and ![]() .
.
The ![]() -intercept is
-intercept is ![]() , as
, as ![]() .
.
Using symmetry, we also have the point ![]() on the graph.
on the graph.
The range is ![]() with a maximum of
with a maximum of ![]() when
when ![]() .
.
Finally we note that ![]() is increasing on
is increasing on ![]() and decreasing on
and decreasing on ![]() .
.
We now generalize the procedure demonstrated in Example 2.1.2. Let ![]() for
for ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} f(x) & = & ax^2 + bx +c \\ [5pt] f(x) - c & = & ax^2 + bx & \text{Subtract $c$ from both sides.}\\ [5pt] \dfrac{f(x)-c}{a} & = & \dfrac{ax^2 + bx}{a} & \text{Divide both sides by $a \neq 0$.} \\ [10pt] \dfrac{f(x)-c}{a} & = & x^2 + \dfrac{b}{a} x & \\ [10pt] \dfrac{f(x)-c}{a} + \left(\dfrac{b}{2a}\right)^2 & = & x^2 + \dfrac{b}{a} x + \left(\dfrac{b}{2a}\right)^2 & \text{Add $ \left(\dfrac{b}{2a}\right)^2 $ to both sides.}\\ [10pt] \dfrac{f(x)-c}{a} + \dfrac{b^2}{4a^2} & = & \left(x + \dfrac{b}{2a}\right)^2 & \text{Factor the perfect square trinomial.} \\ [10pt] \dfrac{f(x)-c}{a} & = & \left(x + \dfrac{b}{2a}\right)^2 - \dfrac{b^2}{4a^2} & \text{Solve for $f(x)$.}\\ [10pt] f(x)-c & = & a \left[ \left(x + \dfrac{b}{2a}\right)^2 - \dfrac{b^2}{4a^2}\right] & \\ [10pt] f(x)-c & = & a\left(x + \dfrac{b}{2a}\right)^2 - a\dfrac{b^2}{4a^2} & \\ [10pt] f(x) & = & a\left(x + \dfrac{b}{2a}\right)^2 - \dfrac{b^2}{4a} + c & \\ [10pt] f(x) & = & a\left(x + \dfrac{b}{2a}\right)^2 + \dfrac{4ac - b^2}{4a} & \text{Get a common denominator.} \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7f8327c7c8cbb22265096c2aeea825b6_l3.png)
By setting ![]() and
and ![]() , we have written the function in the form
, we have written the function in the form ![]() . This establishes the fact that every quadratic function can be written in standard form. Moreover, writing a quadratic function in standard form allows us to identify the vertex rather quickly, and so our work also shows us that the vertex of
. This establishes the fact that every quadratic function can be written in standard form. Moreover, writing a quadratic function in standard form allows us to identify the vertex rather quickly, and so our work also shows us that the vertex of ![]() is
is ![]() . It is not worth memorizing the expression
. It is not worth memorizing the expression ![]() due to the fact that we can write this as
due to the fact that we can write this as ![]() .
.
We summarize the information detailed above in the following box:
Equation 2.1 Vertex Formulas for Quadratic Functions
Suppose ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() are real numbers where
are real numbers where ![]() .
.
- If
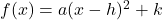 , then the vertex of the graph of
, then the vertex of the graph of 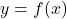 is the point
is the point 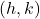 .
. - If
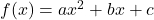 , then the vertex of the graph of
, then the vertex of the graph of 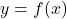 is the point
is the point 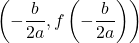 .
.
Completing the square is also the means by which we may derive the celebrated Quadratic Formula, a formula which returns the solutions to ![]() for
for ![]() . Before we state it here for reference, we wish to encourage the reader to pause a moment and read the derivation if the Quadratic Formula found in Section 0.5.5. The work presented in this section transforms the general form of a quadratic function into the standard form whereas the work in Section 0.5.5 finds a formula to solve an equation. There is great value in understanding the similarities and differences between the two approaches.
. Before we state it here for reference, we wish to encourage the reader to pause a moment and read the derivation if the Quadratic Formula found in Section 0.5.5. The work presented in this section transforms the general form of a quadratic function into the standard form whereas the work in Section 0.5.5 finds a formula to solve an equation. There is great value in understanding the similarities and differences between the two approaches.
It is worth pointing out the symmetry inherent in Equation 2.2. We may rewrite the zeros as:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} x &=& \dfrac{-b \pm \sqrt{b^2-4ac}}{2a} \\[8pt] &=& -\dfrac{b}{2a} \pm \dfrac{\sqrt{b^2-4ac}}{2a}, \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-2495cf534da5d2907b4b27aa8c267829_l3.png)
so that, if there are real zeros, they (like the rest of the parabola) are symmetric about the line ![]() . Another way to view this symmetry is that the
. Another way to view this symmetry is that the ![]() -coordinate of the vertex is the average of the zeros. We encourage the reader to verify this fact in all of the preceding examples, where applicable.
-coordinate of the vertex is the average of the zeros. We encourage the reader to verify this fact in all of the preceding examples, where applicable.
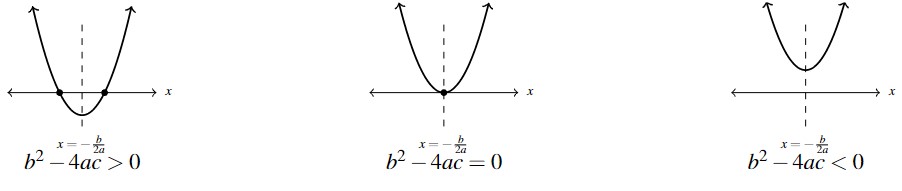
Next, recall that if the quantity ![]() is strictly negative then we do not have any real zeros. This quantity is called the discriminant and is useful in determining the number and nature of solutions to a quadratic equation. We remind the reader of this below.
is strictly negative then we do not have any real zeros. This quantity is called the discriminant and is useful in determining the number and nature of solutions to a quadratic equation. We remind the reader of this below.
Equation 2.3 The Discriminant of a Quadratic Function
Given a quadratic function in general form ![]() , the discriminant is the quantity
, the discriminant is the quantity ![]() .
.
- If
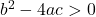 then
then  has two unequal (distinct) real zeros.
has two unequal (distinct) real zeros. - If
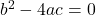 then
then  has one (repeated) real zero.
has one (repeated) real zero. - If If
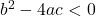 then
then  has two unequal (distinct) non-real zeros.
has two unequal (distinct) non-real zeros.
We’ll talk more about what we mean by a `repeated’ zero and how to compute `non-real’ zeros in Chapter 2. For us, the discriminant has the graphical implication that if ![]() then we have two
then we have two ![]() -intercepts; if
-intercepts; if ![]() then we have just one
then we have just one ![]() -intercept, namely, the vertex; and if
-intercept, namely, the vertex; and if ![]() then we have no
then we have no ![]() -intercepts because the parabola lies entirely above or below the
-intercepts because the parabola lies entirely above or below the ![]() -axis. We sketch each of these scenarios below assuming
-axis. We sketch each of these scenarios below assuming ![]() . (The sketches for
. (The sketches for ![]() are similar.)
are similar.)
We now revisit the economic scenario first described in Examples 1.3.8 and 1.3.9 where we were producing and selling PortaBoy game systems. Recall that the cost to produce ![]() PortaBoys is denoted by
PortaBoys is denoted by ![]() and the price-demand function, that is, the price to charge in order to sell
and the price-demand function, that is, the price to charge in order to sell ![]() systems is denoted by
systems is denoted by ![]() . We introduce two more related functions below: the revenue and profit functions.
. We introduce two more related functions below: the revenue and profit functions.
Definition 2.3 Revenue and Profit
Suppose ![]() represents the cost to produce
represents the cost to produce ![]() units and
units and ![]() is the associated price-demand function. Under the assumption that we are producing the same number of units as are being sold:
is the associated price-demand function. Under the assumption that we are producing the same number of units as are being sold:
- The revenue obtained by selling
 units is
units is 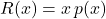 .
.
That is, revenue = (number of items sold) (price per item).
(price per item). - The profit made by selling
 units is
units is 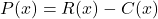 .
.
That is, profit = (revenue) – (cost).
Said differently, the revenue is the amount of money collected by selling ![]() items whereas the profit is how much money is left over after the costs are paid.
items whereas the profit is how much money is left over after the costs are paid.
Example 2.1.3
Example 2.1.3.1
In Example 1.3.8 the cost to produce ![]() PortaBoy game systems for a local retailer was given by
PortaBoy game systems for a local retailer was given by ![]() for
for ![]() and in Example 1.3.9 the price-demand function was found to be
and in Example 1.3.9 the price-demand function was found to be ![]() , for
, for ![]() .
.
Write formulas for the associated revenue and profit functions; include the domain of each.
Solution:
Write formulas for the associated revenue and profit functions, including the domain of each.
The formula for the revenue function is
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} R(x) &=& x \, p(x) \\ &=& x(-1.5x+250) \\ &=& -1.5x^2 + 250x. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-30cd4983538807b8cda3d1a5e372f9c9_l3.png)
The domain of ![]() is restricted to
is restricted to ![]() , and thus the domain of
, and thus the domain of ![]() .
.
To find the profit function ![]() , we subtract
, we subtract
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} P(x) &=& R(x) - C(x) \\ &=& \left(-1.5x^2+250x\right) - \left(80x + 150\right) \\ &=& -1.5x^2+170x-150. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-8a1347b7b6907f35f43d02828847bfa9_l3.png)
The cost function formula is valid for ![]() , but the revenue function is valid when
, but the revenue function is valid when ![]() . Hence, the domain of
. Hence, the domain of ![]() is likewise restricted to
is likewise restricted to ![]() .
.
Example 2.1.3.2
In Example 1.3.8 the cost to produce ![]() PortaBoy game systems for a local retailer was given by
PortaBoy game systems for a local retailer was given by ![]() for
for ![]() and in Example 1.3.9 the price-demand function was found to be
and in Example 1.3.9 the price-demand function was found to be ![]() , for
, for ![]() .
.
Compute and interpret ![]() .
.
Solution:
Compute and interpret ![]() .
.
We find
![]()
This means that if we produce and sell 0 PortaBoy game systems, we have a profit of ![]() 150 dollars.
150 dollars.
As profit = (revenue) ![]() (cost), this means our costs exceed our revenue by 150 dollars. This makes perfect sense, we don’t sell any systems and our revenue is 0 dollars, but our fixed costs (see Example 1.3.8) are 150 dollars.
(cost), this means our costs exceed our revenue by 150 dollars. This makes perfect sense, we don’t sell any systems and our revenue is 0 dollars, but our fixed costs (see Example 1.3.8) are 150 dollars.
Example 2.1.3.3
In Example 1.3.8 the cost to produce ![]() PortaBoy game systems for a local retailer was given by
PortaBoy game systems for a local retailer was given by ![]() for
for ![]() and in Example 1.3.9 the price-demand function was found to be
and in Example 1.3.9 the price-demand function was found to be ![]() , for
, for ![]() .
.
Compute and interpret the zeros of ![]() .
.
Solution:
Compute and interpret the zeros of ![]() .
.
To find the zeros of ![]() , we set
, we set ![]() and solve
and solve ![]() . Factoring here would be challenging to say the least, so we use the Quadratic Formula, Equation 2.2. Identifying
. Factoring here would be challenging to say the least, so we use the Quadratic Formula, Equation 2.2. Identifying ![]() ,
, ![]() and
and ![]() , we obtain
, we obtain
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} x & = & \dfrac{-b \pm \sqrt{b^2-4ac}}{2a} & \\ [10pt] & = & \dfrac{-170 \pm \sqrt{170^2 - 4(-1.5)(-150)}}{2(-1.5)} & \\ [10pt] \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-acd387ab51f74f5719884ff314f47dc2_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} x & = & \dfrac{-170 \pm \sqrt{28000}}{-3} & \\ [10pt] & = & \dfrac{170 \pm 20 \sqrt{70}}{3} & \\ [10pt] & \approx & 0.89, \, 112.44. \\ & & \phantom{\dfrac{-170 \pm \sqrt{170^2 - 4(-1.5)(-150)}}{2(-1.5)} }& \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e8c9e7cdd978a6e99e30b8fdfa0ba788_l3.png)
Given that profit = (revenue) ![]() (cost), if profit = 0, then revenue = cost. Hence, the zeros of
(cost), if profit = 0, then revenue = cost. Hence, the zeros of ![]() are called the `break-even’ points – where just enough product is sold to recover the cost spent to make the product. Also,
are called the `break-even’ points – where just enough product is sold to recover the cost spent to make the product. Also, ![]() represents a number of game systems, which is a whole number, so instead of using the exact values of the zeros, or even their approximations, we consider
represents a number of game systems, which is a whole number, so instead of using the exact values of the zeros, or even their approximations, we consider ![]() and
and ![]() along with
along with ![]() and
and ![]() .
.
We find ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
These data suggest that, in order to be profitable, at least 1 but not more than 112 systems should be produced and sold, as borne out in number 4.
Example 2.1.3.4
In Example 1.3.8 the cost to produce ![]() PortaBoy game systems for a local retailer was given by
PortaBoy game systems for a local retailer was given by ![]() for
for ![]() and in Example 1.3.9 the price-demand function was found to be
and in Example 1.3.9 the price-demand function was found to be ![]() , for
, for ![]() .
.
Graph ![]() . Find the vertex and axis intercepts.
. Find the vertex and axis intercepts.
Solution:
Graph ![]() . Find the vertex and axis intercepts.
. Find the vertex and axis intercepts.
Knowing the zeros of ![]() , we have two
, we have two ![]() -intercepts:
-intercepts: ![]() and
and ![]() .
.
As ![]() , we get the
, we get the ![]() -intercept is
-intercept is ![]() .
.
To find the vertex, we appeal to Equation 2.1. Substituting ![]() and
and ![]() , we get
, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} x &=& -\frac{170}{2(-1.5)} \\[6pt] &=& \frac{170}{3} \\[6pt] &=& 56.\overline{6} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-320c4d9f633331ed6c8cde83735b7402_l3.png)
To find the ![]() -coordinate of the vertex, we compute
-coordinate of the vertex, we compute
![]()
Hence, the vertex is ![]() .
.
The domain is restricted ![]() and we find
and we find ![]() . Attempting to plot all of these points on the same graph to any sort of scale is challenging. Instead, we present a portion of the graph for
. Attempting to plot all of these points on the same graph to any sort of scale is challenging. Instead, we present a portion of the graph for ![]() . Even with this, the intercepts near the origin are crowded.
. Even with this, the intercepts near the origin are crowded.
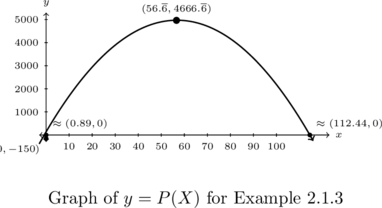
Example 2.1.3.5
In Example 1.3.8 the cost to produce ![]() PortaBoy game systems for a local retailer was given by
PortaBoy game systems for a local retailer was given by ![]() for
for ![]() and in Example 1.3.9 the price-demand function was found to be
and in Example 1.3.9 the price-demand function was found to be ![]() , for
, for ![]() .
.
Interpret the vertex of the graph of ![]() .
.
Solution:
Interpret the vertex of the graph of ![]() .
.
From the vertex, we see that the maximum of ![]() is
is ![]() when
when ![]() . As before,
. As before, ![]() represents the number of PortaBoy systems produced and sold, so we cannot produce and sell
represents the number of PortaBoy systems produced and sold, so we cannot produce and sell ![]() systems.
systems.
Hence, by comparing ![]() and
and ![]() , we conclude that we will make a maximum profit of 4666.50 dollars if we sell 57 game systems.
, we conclude that we will make a maximum profit of 4666.50 dollars if we sell 57 game systems.
Example 2.1.3.6
In Example 1.3.8 the cost to produce ![]() PortaBoy game systems for a local retailer was given by
PortaBoy game systems for a local retailer was given by ![]() for
for ![]() and in Example 1.3.9 the price-demand function was found to be
and in Example 1.3.9 the price-demand function was found to be ![]() , for
, for ![]() .
.
What should the price per system be in order to maximize profit?
Solution:
What should the price per system be in order to maximize profit?
We’ve determined that we need to sell 57 PortaBoys to maximize profit, so we substitute ![]() into the price-demand function to get
into the price-demand function to get ![]() .
.
In other words, to sell 57 systems, and thereby maximize the profit, we should set the price at 164.50 dollars per system.
Example 2.1.3.7
In Example 1.3.8 the cost to produce ![]() PortaBoy game systems for a local retailer was given by
PortaBoy game systems for a local retailer was given by ![]() for
for ![]() and in Example 1.3.9 the price-demand function was found to be
and in Example 1.3.9 the price-demand function was found to be ![]() , for
, for ![]() .
.
Compute and interpret the average rate of change of ![]() over the interval
over the interval ![]() .
.
Solution:
Compute and interpret the average rate of change of ![]() over the interval
over the interval ![]() .
.
To find the average rate of change of ![]() over
over ![]() , we compute
, we compute
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \dfrac{\Delta [P(x)]}{\Delta x} &=& \dfrac{P(57) - P(0)}{57-0} \\[8pt] &=& \dfrac{4666.5 - (-150)}{57} \\[8pt] &=& 84.5 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-85e6fad65a9212afa8b6367e4045eb3a_l3.png)
This means that as the number of systems produced and sold ranges from 0 to 57, the average profit per system is increasing at a rate of 84.50 dollars. In other words, for each additional system produced and sold, the profit increased by 84.50 dollars on average.
We hope Example 2.1.3 shows the value of using a continuous model to describe a discrete situation. True, we could have `run the numbers’ and computed ![]() to eventually determine the maximum profit, but the vertex formula made much quicker work of the problem.
to eventually determine the maximum profit, but the vertex formula made much quicker work of the problem.
Our next example is classic application of optimizing a quadratic function.
Example 2.1.4
Example 2.1.3.7
Much to Donnie’s surprise and delight, he inherits a large parcel of land in Ashtabula County from one of his (e)strange(d) relatives so the time is right for him to pursue his dream of raising alpaca. He wishes to build a rectangular pasture and estimates that he has enough money for 200 linear feet of fencing material. If he makes the pasture adjacent to a river (so that no fencing is required on that side), what are the dimensions of the pasture which maximize the area? What is the maximum area? If an average alpaca needs 25 square feet of grazing area, how many alpaca can Donnie keep in his pasture?
Solution:
We are asked to determine the dimensions of the pasture which would give a maximum area, so we begin by sketching the diagram seen below.

We let ![]() denote the width of the pasture and we let
denote the width of the pasture and we let ![]() denote the length of the pasture. The units given to us in the statement of the problem are feet, so we assume that
denote the length of the pasture. The units given to us in the statement of the problem are feet, so we assume that ![]() and
and ![]() are measured in feet. The area of the pasture, which we’ll call
are measured in feet. The area of the pasture, which we’ll call ![]() , is related to
, is related to ![]() and
and ![]() by the equation
by the equation ![]() . Given
. Given ![]() and
and ![]() are both measured in feet,
are both measured in feet, ![]() has units of
has units of ![]() , or square feet.
, or square feet.
We are also told that the total amount of fencing available is ![]() feet, which means
feet, which means ![]() , or,
, or, ![]() .
.
We now have two equations, ![]() and
and ![]() .
.
In order to use the tools given to us in this section to maximize ![]() , we need to use the information given to write
, we need to use the information given to write ![]() as a function of just one variable, either
as a function of just one variable, either ![]() or
or ![]() . This is where we use the equation
. This is where we use the equation ![]() . Solving for
. Solving for ![]() , we find
, we find ![]() , and we substitute this into our equation for
, and we substitute this into our equation for ![]() . We get
. We get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} A &=& w \ell \\ &=& w(200-2w) \\ &=& 200w-2w^2 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d4a392605d5a0fbdce2b1e6ae9d05d7d_l3.png)
We now have ![]() as a function of
as a function of ![]() ,
,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} A &=& f(w) \\ &=& 200w-2w^2 \\ &=& -2w^2+200w \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-77a233e19f2e8548e1ac64e9df5e770f_l3.png)
Before we go any further, we need to find the applied domain of ![]() so that we know what values of
so that we know what values of ![]() make sense in this situation.[5] Given that
make sense in this situation.[5] Given that ![]() represents the width of the pasture we need
represents the width of the pasture we need ![]() .
.
Likewise, ![]() represents the length of the pasture, so
represents the length of the pasture, so ![]() . Solving this latter inequality yields
. Solving this latter inequality yields ![]() .
.
Hence, the function we wish to maximize is ![]() for
for ![]() . We know two things about the quadratic function
. We know two things about the quadratic function ![]() : the graph of
: the graph of ![]() is a parabola and (with the coefficient of
is a parabola and (with the coefficient of ![]() being
being ![]() ) the parabola opens downwards.
) the parabola opens downwards.

This means that there is a maximum value to be found, and we know it occurs at the vertex. Using the vertex formula, we find
![]()
and
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} A &=& f(50) \\ &=& -2(50)^2 + 200(50)\\ &=& 5000 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-eaee9160b0d4861f770b35cc8cc40b16_l3.png)
![]() lies in the applied domain,
lies in the applied domain, ![]() , thus we have that the area of the pasture is maximized when the width is
, thus we have that the area of the pasture is maximized when the width is ![]() feet.
feet.
To find the length, we use ![]() and find
and find ![]() , so the length of the pasture is
, so the length of the pasture is ![]() feet.
feet.
The maximum area is ![]() , or
, or ![]() square feet. If an average alpaca requires 25 square feet of pasture, Donnie can raise
square feet. If an average alpaca requires 25 square feet of pasture, Donnie can raise ![]() average alpaca.
average alpaca.
The function ![]() in Example 2.1.4 is called the objective function for this problem – it’s the function we’re trying to optimize. In the case above, we were trying to maximize
in Example 2.1.4 is called the objective function for this problem – it’s the function we’re trying to optimize. In the case above, we were trying to maximize ![]() . The equation
. The equation ![]() along with the inequalities
along with the inequalities ![]() and
and ![]() are called the constraints. As we saw in this example, and as we’ll see again and again, the constraint equation is used to rewrite the objective function in terms of just one of the variables where constraint inequalities, if any, help determine the applied domain.
are called the constraints. As we saw in this example, and as we’ll see again and again, the constraint equation is used to rewrite the objective function in terms of just one of the variables where constraint inequalities, if any, help determine the applied domain.
2.1.2 Section Exercises
In Exercises 1 – 9, graph the quadratic function. Determine the vertex and axis intercepts of each graph, if they exist. State the domain and range, identify the maximum or minimum, and list the intervals over which the function is increasing or decreasing. If the function is given in general form, convert it into standard form; if it is given in standard form, convert it into general form.
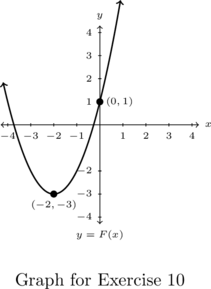
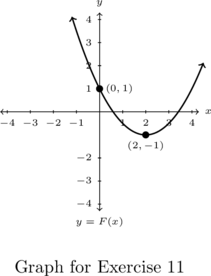
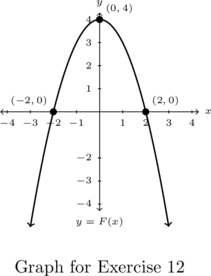
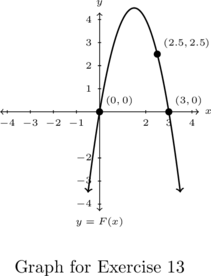
In Exercises 10 – 13, write a formula for each function below in the form ![]() .
.
In Exercises 14 – 18, cost and price-demand functions are given. For each scenario,
- Determine the profit function
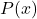 .
. - Compute the number of items which need to be sold in order to maximize profit.
- Calculate the maximum profit.
- Calculate the price to charge per item in order to maximize profit.
- Identify and interpret break-even points.
- The cost, in dollars, to produce
 “I’d rather be a Sasquatch” T-Shirts is
“I’d rather be a Sasquatch” T-Shirts is 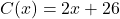 ,
, 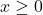 and the price-demand function, in dollars per shirt, is
and the price-demand function, in dollars per shirt, is 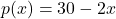 , for
, for 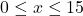 .
. - The cost, in dollars, to produce
 bottles of
bottles of 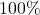 All-Natural Certified Free-Trade Organic Sasquatch Tonic is
All-Natural Certified Free-Trade Organic Sasquatch Tonic is 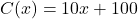 ,
, 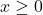 and the price-demand function, in dollars per bottle, is
and the price-demand function, in dollars per bottle, is 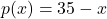 , for
, for 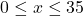 .
. - The cost, in cents, to produce
 cups of Mountain Thunder Lemonade at Junior’s Lemonade Stand is
cups of Mountain Thunder Lemonade at Junior’s Lemonade Stand is 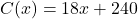 ,
, 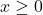 and the price-demand function, in cents per cup, is
and the price-demand function, in cents per cup, is 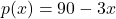 , for
, for 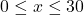 .
. - The daily cost, in dollars, to produce
 Sasquatch Berry Pies is
Sasquatch Berry Pies is 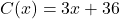 ,
, 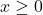 and the price-demand function, in dollars per pie, is
and the price-demand function, in dollars per pie, is 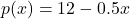 , for
, for 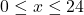 .
. - The monthly cost, in hundreds of dollars, to produce
 custom built electric scooters is
custom built electric scooters is 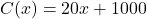 ,
, 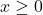 and the price-demand function, in hundreds of dollars per scooter, is
and the price-demand function, in hundreds of dollars per scooter, is 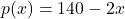 , for
, for 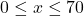 .
. - The International Silver Strings Submarine Band holds a bake sale each year to fund their trip to the National Sasquatch Convention. It has been determined that the cost in dollars of baking
 cookies is
cookies is 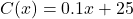 and that the demand function for their cookies is
and that the demand function for their cookies is 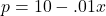 for
for  . How many cookies should they bake in order to maximize their profit?
. How many cookies should they bake in order to maximize their profit? - Using data from Bureau of Transportation Statistics, the average fuel economy
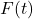 in miles per gallon for passenger cars in the US
in miles per gallon for passenger cars in the US  years after 1980 can be modeled by
years after 1980 can be modeled by 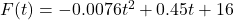 ,
, 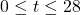 . Find and interpret the coordinates of the vertex of the graph of
. Find and interpret the coordinates of the vertex of the graph of 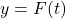 .
. - The temperature
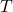 , in degrees Fahrenheit,
, in degrees Fahrenheit,  hours after 6 AM is given by:
hours after 6 AM is given by:
![Rendered by QuickLaTeX.com \[ T(t) = -\frac{1}{2} t^2 + 8t+32, \quad 0 \leq t \leq 12\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-66152fdb330bc508479760da9d9022f3_l3.png)
What is the warmest temperature of the day? When does this happen?
- Suppose
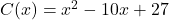 represents the costs, in hundreds, to produce
represents the costs, in hundreds, to produce  thousand pens. How many pens should be produced to minimize the cost? What is this minimum cost?
thousand pens. How many pens should be produced to minimize the cost? What is this minimum cost? - Skippy wishes to plant a vegetable garden along one side of his house. In his garage, he found 32 linear feet of fencing. Due to the fact that one side of the garden will border the house, Skippy doesn’t need fencing along that side. What are the dimensions of the garden which will maximize the area of the garden? What is the maximum area of the garden?
- In the situation of Example 2.1.4, Donnie has a nightmare that one of his alpaca fell into the river. To avoid this, he wants to move his rectangular pasture away from the river so that all four sides of the pasture require fencing. If the total amount of fencing available is still 200 linear feet, what dimensions maximize the area of the pasture now? What is the maximum area? Assuming an average alpaca requires 25 square feet of pasture, how many alpaca can he raise now?
- What is the largest rectangular area one can enclose with 14 inches of string?
- The two towers of a suspension bridge are 400 feet apart. The parabolic cable[6] attached to the tops of the towers is 10 feet above the point on the bridge deck that is midway between the towers. If the towers are 100 feet tall, find the height of the cable directly above a point of the bridge deck that is 50 feet to the right of the left-hand tower.
In Exercises 27 – 32, solve the quadratic equation for the indicated variable.
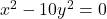 for
for 
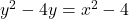 for
for 
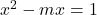 for
for 
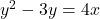 for
for 
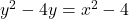 for
for 
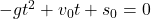 for
for  (Assume
(Assume 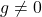 .)
.)- (This is a follow-up to Exercise 96 in Section 1.3.1.) The Lagrange Interpolate function
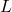 for three points
for three points 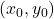 ,
, 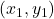 , and
, and 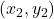 where
where 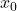 ,
, 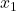 , and
, and 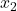 are three distinct real numbers is given by:
are three distinct real numbers is given by:
![Rendered by QuickLaTeX.com \[L(x) = y_{0} \dfrac{(x - x_{1}) (x - x_{2}) }{(x_{0} - x_{1})(x_{0} - x_{2})}+ y_{1} \dfrac{(x - x_{0}) (x - x_{2}) }{(x_{1} - x_{0})(x_{1} - x_{2})} + y_{2} \dfrac{(x - x_{0}) (x - x_{1}) }{(x_{2} - x_{0})(x_{2} - x_{1})}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-aa739c0dfbaca32bb85c4a2883653b0d_l3.png)
- For each of the following sets of points, find
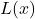 using the formula above and verify each of the points lies on the graph of
using the formula above and verify each of the points lies on the graph of 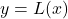 .
.
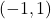 ,
, 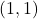 ,
, 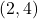
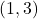 ,
, 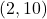 ,
, 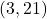
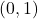 ,
, 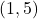 ,
, 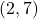
- Verify that, in general,
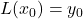 ,
, 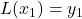 , and
, and 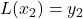 .
. - Find
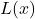 for the points
for the points 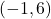 ,
, 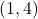 and
and 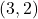 . What happens?
. What happens? - Under what conditions will
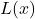 produce a quadratic function? Make a conjecture, test some cases, and prove your answer.
produce a quadratic function? Make a conjecture, test some cases, and prove your answer.
- For each of the following sets of points, find
Section 2.1 Exercise Answers can be found in the Appendix … Coming soon
- This assumes, of course,
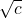 is a real number for all real numbers
is a real number for all real numbers 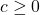 \ldots ↵
\ldots ↵ - i.e., replace
 with
with 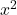 ,
, 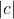 with
with 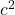 ,
, 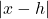 with
with 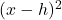 . ↵
. ↵ - and get common denominators! ↵
- The reader is encouraged to compare this example with number 2 of Example 1.4.2. ↵
- Donnie would be very upset if, for example, we told him the width of the pasture needs to be
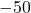 feet. ↵
feet. ↵ - The weight of the bridge deck forces the bridge cable into a parabola and a free hanging cable such as a power line does not form a parabola. We shall see in an exercise in Section 5.7 what shape a free hanging cable makes. ↵
A function of one variable with with the highest power is a two.
A function that is being optimized.
The inequalities which restrict or place conditions on the variables variables of an objective function.