2.3 Real Zeros of Polynomials
We now turn our attention to polynomial long division. Dividing two polynomials follows the same algorithm, in principle, as dividing two natural numbers so we review that process first. Suppose we wished to divide ![]() by
by ![]() . The standard division tableau is given below.
. The standard division tableau is given below.
![Rendered by QuickLaTeX.com \[ \begin{array}{cccccc} & & & & 3 & 2 \\ \hhline{~~|----} 7 & 9 \, \vline & \, 2 & 5 & 8 & 5 \\ & -& 2 & 3 & 7 & \downarrow \\ \hhline{~~---} & & & 2 & 1 & 5 \\ & & - & 1 & 5 & 8 \\ \hhline{~~~---} & & & & 5 & 7 \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b93ac7fd7d05c5a4ad9add3ca6b7fddb_l3.png)
In this case, ![]() is called the divisor, 2585 is called the dividend, 32 is called the quotient and
is called the divisor, 2585 is called the dividend, 32 is called the quotient and ![]() is called the remainder. We can check our answer by showing:
is called the remainder. We can check our answer by showing:
dividend = (divisor)(quotient) + remainder
or in this case, ![]() . We hope that the long division tableau evokes warm, fuzzy memories of your formative years as opposed to feelings of hopelessness and frustration. If you experience the latter, keep in mind that the Division Algorithm essentially is a two-step process, iterated over and over again. First, we guess the number of times the divisor goes into the dividend and then we subtract off our guess. We repeat those steps with what’s left over until what’s left over (the remainder) is less than what we started with (the divisor). That’s all there is to it!
. We hope that the long division tableau evokes warm, fuzzy memories of your formative years as opposed to feelings of hopelessness and frustration. If you experience the latter, keep in mind that the Division Algorithm essentially is a two-step process, iterated over and over again. First, we guess the number of times the divisor goes into the dividend and then we subtract off our guess. We repeat those steps with what’s left over until what’s left over (the remainder) is less than what we started with (the divisor). That’s all there is to it!
The division algorithm for polynomials has the same basic two steps but when we subtract polynomials, we must take care to subtract like terms only. As a transition to polynomial division, let’s write out our previous division tableau in expanded form.
![Rendered by QuickLaTeX.com \[ \begin{array}{cccccccccc} & & & & & & & 3 \cdot 10 & + & 2 \\ \hhline{~~~|-------} 7 \cdot 10 & + & 9 \, \vline& 2\cdot 10^3 & + & 5 \cdot 10^2 & + & 8 \cdot 10 & + & 5 \\ & & -& \left(2 \cdot 10^3 \right. & + & 3 \cdot 10^2 & + & \left. 7 \cdot 10 \right) & & \downarrow \\ \hhline{~~~-----~~} & & & & & 2 \cdot 10^2 & + & 1 \cdot 10 & + & 5 \\ & & & & - & \left(1 \cdot 10^2 \right. & + & 5 \cdot 10 & + &\left. 8 \right) \\ \hhline{~~~~~---~~} & & & & & & & 5 \cdot 10 & + & 7 \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-962a2060ebf5872b16e3c862c5c934ec_l3.png)
Written this way, we see that when we line up the digits we are really lining up the coefficients of the corresponding powers of ![]() – much like how we’ll have to keep the powers of
– much like how we’ll have to keep the powers of ![]() lined up in the same columns. The big difference between polynomial division and the division of natural numbers is that the value of
lined up in the same columns. The big difference between polynomial division and the division of natural numbers is that the value of ![]() is an unknown quantity. So unlike using the known value of
is an unknown quantity. So unlike using the known value of ![]() , when we subtract there can be no regrouping of coefficients as in our previous example. (The subtraction
, when we subtract there can be no regrouping of coefficients as in our previous example. (The subtraction ![]() requires us to `regroup’ or `borrow’ from the tens digit, then the hundreds digit.) This actually makes polynomial division easier.[1] Before we dive into examples, we first state a theorem telling us when we can divide two polynomials, and what to expect when we do so.
requires us to `regroup’ or `borrow’ from the tens digit, then the hundreds digit.) This actually makes polynomial division easier.[1] Before we dive into examples, we first state a theorem telling us when we can divide two polynomials, and what to expect when we do so.
Theorem 2.8 Polynomial Division
Suppose ![]() and
and ![]() are nonzero polynomial functions where the degree of
are nonzero polynomial functions where the degree of ![]() is greater than or equal to the degree of
is greater than or equal to the degree of ![]() . There exist two unique polynomial functions,
. There exist two unique polynomial functions, ![]() and
and ![]() , such that
, such that
![]()
where either ![]() or the degree of
or the degree of ![]() is strictly less than the degree of
is strictly less than the degree of ![]() .
.
Essentially, Theorem 2.8 tells us that we can divide polynomials whenever the degree of the divisor is less than or equal to the degree of the dividend. We know we’re done with the division when the polynomial left over (the remainder) has a degree strictly less than the divisor. It’s time to walk through a few examples.
Example 2.3.1
Example 2.3.1.1
Perform the indicated division.
![]()
Check your answer by showing
![]()
Solution:
Simplify ![]() .
.
o begin ![]() , we divide the first term in the dividend, namely
, we divide the first term in the dividend, namely ![]() , by the first term in the divisor, namely
, by the first term in the divisor, namely ![]() , and get
, and get ![]() . This then becomes the first term in the quotient. We proceed as in regular long division at this point: we multiply the entire divisor,
. This then becomes the first term in the quotient. We proceed as in regular long division at this point: we multiply the entire divisor, ![]() , by this first term in the quotient to get
, by this first term in the quotient to get ![]() . We then subtract this result from the dividend.
. We then subtract this result from the dividend.
![Rendered by QuickLaTeX.com \[ \begin{array}{cccccccccc} & & & & & x^2 & & & & \\ \hhline{~~~|-------} x & - & 2 \, \vline& x^3 & + & 4x^2 & - & 5x & - & 14 \\ & & -& \left(x^3 \right. & - & \left. 2x^2\right) & & \downarrow & & \\ \hhline{~~~---~~~~} & & & & & 6 x^2 & - & 5x & & \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c412358f495fe72680a96b6260c4641f_l3.png)
Now we `bring down’ the next term of the quotient, namely ![]() , and repeat the process. We divide
, and repeat the process. We divide ![]() , and add this to the quotient polynomial, multiply it by the divisor (which yields
, and add this to the quotient polynomial, multiply it by the divisor (which yields ![]() ) and subtract.
) and subtract.
![Rendered by QuickLaTeX.com \[ \begin{array}{cccccccccc} & & & & & x^2 & + & 6x & & \\ \hhline{~~~|-------} x & - & 2 \, \vline& x^3 & + & 4x^2 & - & 5x & - & 14 \\ & & -& \left(x^3 \right. & - & \left. 2x^2\right) & & & & \downarrow \\ \hhline{~~~---~~~~} & & & & & 6 x^2 & - & 5x & & \downarrow \\ & & & & - & \left(6 x^2 \right. & - & \left. 12x \right) & & \downarrow \\ \hhline{~~~~~---~~} & & & & & & & 7x & - & 14 \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-3e2f70656b6adeeb808523d80dddf222_l3.png)
Finally, we `bring down’ the last term of the dividend, namely ![]() , and repeat the process. We divide
, and repeat the process. We divide ![]() , add this to the quotient, multiply it by the divisor (which yields
, add this to the quotient, multiply it by the divisor (which yields ![]() ) and subtract.
) and subtract.
![Rendered by QuickLaTeX.com \[ \begin{array}{cccccccccc} & & & & & x^2 & + & 6x & + & 7 \\ \hhline{~~~|-------} x & - & 2 \, \vline& x^3 & + & 4x^2 & - & 5x & - & 14 \\ & & -& \left(x^3 \right. & - & \left. 2x^2\right) & & & & \\ \hhline{~~~---~~~~} & & & & & 6 x^2 & - & 5x & & \\ & & & & - & \left(6 x^2 \right. & - & \left. 12x \right) & & \\ \hhline{~~~~~---~~} & & & & & & & 7x & - & 14 \\ & & & & & & - & \left( 7x \right. & - & \left. 14 \right) \\ \hhline{~~~~~~~---} & & & & & & & & & 0 \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b0c640b3978cf60be9f7a35e9d0f02b8_l3.png)
In this case, we get a quotient of ![]() with a remainder of
with a remainder of ![]() .
.
To check our answer, we compute
![]()
Example 2.3.1.2
Perform the indicated division.
![]()
Check your answer by showing
![]()
Solution:
Simplify ![]() .
.
To compute ![]() , we start as before. We find
, we start as before. We find ![]() , so that becomes the first (and only) term in the quotient. We multiply the divisor
, so that becomes the first (and only) term in the quotient. We multiply the divisor ![]() by
by ![]() and get
and get ![]() . We subtract this from the divided and get
. We subtract this from the divided and get ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{cccccc} & & & & & \dfrac{2}{3} \\ \hhline{~~~|---} 3t & - & 4 \, \vline& 2t & + & 7 \\ & & -& \left(2t\vphantom{\dfrac{8}{3}} \right. & - & \left. \dfrac{8}{3}\right) \\ \hhline{~~~---} & & & & & \dfrac{29}{3} \vphantom{\sqrt{\dfrac{7}{7}}} \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-741c15fbd68c4c4834b00dd0dfdf88ce_l3.png)
Our answer is ![]() with a remainder of
with a remainder of ![]() .
.
To check our answer, we compute
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} (3t-4) \left(\frac{2}{3}\right) + \frac{29}{3} &=& 2t - \frac{8}{3} + \frac{29}{3} \\ &=& 2t + \frac{21}{3} \\ &=& 2t + 7 \, \checkmark \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5bbc9a4e73e61b772ed16fb23adb9084_l3.png)
Example 2.3.1.3
Perform the indicated division.
![]()
Check your answer by showing
![]()
Solution:
Simplify ![]() .
.
When we set-up the tableau for ![]() , we must first issue a `placeholder’ for the `missing’
, we must first issue a `placeholder’ for the `missing’ ![]() -term in the dividend,
-term in the dividend, ![]() . We then proceed as before.
. We then proceed as before. ![]() , thus
, thus ![]() is the first term in our quotient. We multiply
is the first term in our quotient. We multiply ![]() times
times ![]() and subtract it from the dividend. We bring down the
and subtract it from the dividend. We bring down the ![]() , and repeat.
, and repeat.
![Rendered by QuickLaTeX.com \[ \begin{array}{cccccccc} & & & & & 3y & - & \dfrac{15}{2} \\ \hhline{~~~|-----} 2y& + & 5 \, \vline& 6y^2 & + & 0y & - & 1 \\ & & -& \left(6y^2 \right. & + & \left. 15y\right) & & \downarrow \\ \hhline{~~~---~~} & & & & & -15y & - & 1 \\ & & & & - & \left(-15y\vphantom{\dfrac{75}{2}} \right. & - & \left. \dfrac{75}{2} \right) \\ \hhline{~~~~~---} & & & & & & & \dfrac{73}{2} \vphantom{\sqrt{\dfrac{73}{2}}}\\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-530ab659ee2c14454e8f4812c2354026_l3.png)
Our answer is ![]() with a remainder of
with a remainder of ![]() .
.
To check our answer, we compute:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} (2y + 5)\left(3y - \dfrac{15}{2}\right) + \dfrac{73}{2} &=& 6y^2 - 15y + 15y - \dfrac{75}{2} + \dfrac{73}{2} \\ &=& 6y^2 - 1 \, \checkmark \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7c437942453dea3a42979d7e2fc061e0_l3.png)
Example 2.3.1.4
Perform the indicated division.
![]()
Check your answer by showing
![]()
Solution:
Simplify ![]() .
.
For our last example, we need `placeholders’ for both the divisor ![]() and the dividend
and the dividend ![]() . The first term in the quotient is
. The first term in the quotient is ![]() , and when we multiply and subtract this from the dividend, we’re left with just
, and when we multiply and subtract this from the dividend, we’re left with just ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{cccccccccccc} & & & & & & & & & w & & \\ \hhline{~~~~~|-------} w^2 & + & 0w & - & \sqrt{2} \, \vline & w^3 & + & 0w^2 & + & 0w & + & 0 \\ & & & & -&\left(w^3\vphantom{w\sqrt{2}} \right. & + & 0w^2 & - & \left. w\sqrt{2} \right) & & \downarrow \\ \hhline{~~~~~-----~~} & & & & & & & 0w^2 & + & w\sqrt{2} & + & 0\\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b67dfd91c9588e5c51f026eb7db57a6c_l3.png)
The degree of ![]() (which is
(which is ![]() ) is less than the degree of the divisor (which is
) is less than the degree of the divisor (which is ![]() ), therefore we are done.[2]
), therefore we are done.[2]
Our answer is ![]() with a remainder of
with a remainder of ![]() .
.
To check, we compute:
![]()
As you may recall, all of the polynomials in Theorem 2.8 have special names. The polynomial ![]() is called the dividend;
is called the dividend; ![]() is the divisor;
is the divisor; ![]() is the quotient;
is the quotient; ![]() is the remainder. If
is the remainder. If ![]() then
then ![]() is called a factor of
is called a factor of ![]() . The word `unique’ here is critical in that it guarantees there is only one quotient and remainder for each division problem.[3] The proof of Theorem 2.8 is usually relegated to a course in Abstract Algebra, but we can still use the result to establish two important facts which are the basis of the rest of the section.
. The word `unique’ here is critical in that it guarantees there is only one quotient and remainder for each division problem.[3] The proof of Theorem 2.8 is usually relegated to a course in Abstract Algebra, but we can still use the result to establish two important facts which are the basis of the rest of the section.
Theorem 2.9 The Remainder Theorem
Suppose ![]() is a polynomial function of degree at least
is a polynomial function of degree at least ![]() and
and ![]() is a real number. When
is a real number. When ![]() is divided by
is divided by ![]() the remainder is
the remainder is ![]() . Said differently, there is a polynomial function
. Said differently, there is a polynomial function ![]() such that:
such that:
![]()
The proof of Theorem 2.9 is a direct consequence of Theorem 2.8. Due to the fact that ![]() has degree
has degree ![]() , when a polynomial function is divided by
, when a polynomial function is divided by ![]() , the remainder is either
, the remainder is either ![]() or degree
or degree ![]() (i.e., a nonzero constant.) In either case,
(i.e., a nonzero constant.) In either case, ![]() , where
, where ![]() , the remainder, is a real number, possibly
, the remainder, is a real number, possibly ![]() . It follows that
. It follows that ![]() , so we get
, so we get ![]() as required. There is one last `low hanging fruit’ to collect which we present below.
as required. There is one last `low hanging fruit’ to collect which we present below.
Theorem 2.10 The Factor Theorem
Suppose ![]() is a nonzero polynomial function. The real number
is a nonzero polynomial function. The real number ![]() is a zero of
is a zero of ![]() if and only if
if and only if ![]() is a factor of
is a factor of ![]() .
.
Once again, we see the phrase `if and only if’ which means there are really two things being said in The Factor Theorem: if ![]() is a factor of
is a factor of ![]() , then
, then ![]() is a zero of
is a zero of ![]() and the only way
and the only way ![]() is a zero of
is a zero of ![]() is if
is if ![]() is a factor of
is a factor of ![]() . We argue the Factor Theorem as follows: if
. We argue the Factor Theorem as follows: if ![]() is a factor of
is a factor of ![]() , then
, then ![]() for some polynomial
for some polynomial ![]() . Hence,
. Hence, ![]() , so
, so ![]() is a zero of
is a zero of ![]() . Conversely, suppose
. Conversely, suppose ![]() is a zero of
is a zero of ![]() , so
, so ![]() . The Remainder Theorem tells us
. The Remainder Theorem tells us ![]() . Hence,
. Hence, ![]() is a factor of
is a factor of ![]() .
.
We have enough theory to explain why the concept of multiplicity (Definition 2.9) is well-defined. If ![]() is a zero of
is a zero of ![]() , then The Factor Theorem tells us there is a polynomial function
, then The Factor Theorem tells us there is a polynomial function ![]() so that
so that ![]() . If
. If ![]() , then we apply the Factor Theorem to
, then we apply the Factor Theorem to ![]() and find a polynomial
and find a polynomial ![]() so that
so that ![]() . Hence, we have
. Hence, we have
![]()
We now `rinse and repeat’ this process. The degree of ![]() is a finite number, so this process has to end at some point. That is we arrive at a factorization
is a finite number, so this process has to end at some point. That is we arrive at a factorization ![]() where
where ![]() . Suppose we arrive at a different factorization of
. Suppose we arrive at a different factorization of ![]() using other methods. That is, we find
using other methods. That is, we find ![]() , where
, where ![]() is a polynomial function with
is a polynomial function with ![]() . Then we have
. Then we have ![]() . If
. If ![]() , then either
, then either ![]() or
or ![]() . Assuming the former, then we may divide both sides by
. Assuming the former, then we may divide both sides by ![]() to get:
to get: ![]() . Because
. Because ![]() ,
, ![]() and we would have
and we would have ![]() , a contradiction as we are assuming
, a contradiction as we are assuming ![]() . The assumption that
. The assumption that ![]() likewise ends in a contradiction. Therefore, we have
likewise ends in a contradiction. Therefore, we have ![]() , so
, so ![]() . By the uniqueness guaranteed in Theorem 2.8, we must have that
. By the uniqueness guaranteed in Theorem 2.8, we must have that ![]() . Hence, we have shown the number
. Hence, we have shown the number ![]() , as well as the quotient polynomial
, as well as the quotient polynomial ![]() are unique. The process outlined above, in which we coax out factors of
are unique. The process outlined above, in which we coax out factors of ![]() one at a time until we have all of them serves as a template for our work to come.
one at a time until we have all of them serves as a template for our work to come.
Of the things The Factor Theorem tells us, the most pragmatic is that we had better find a more efficient way to divide polynomial functions by quantities of the form ![]() . Fortunately, people like Ruffini and Horner have already blazed this trail. Let’s take a closer look at the long division we performed at the beginning of the section and try to streamline it. First off, let’s change all of the subtractions into additions by distributing through the
. Fortunately, people like Ruffini and Horner have already blazed this trail. Let’s take a closer look at the long division we performed at the beginning of the section and try to streamline it. First off, let’s change all of the subtractions into additions by distributing through the ![]() s.
s.
![Rendered by QuickLaTeX.com \[ \begin{array}{cccccccccc} & & & & & x^2 & + & 6x & + & 7 \\ \hhline{~~~|-------} x & - & 2 \, \vline& x^3 & + & 4x^2 & - & 5x & - & 14 \\ & & & -x^3 & + & 2x^2 & & & & \\ \hhline{~~~---~~~~} & & & & & 6 x^2 & - & 5x & & \\ & & & & &-6 x^2 & + & 12x & & \\ \hhline{~~~~~---~~} & & & & & & & 7x & - & 14 \\ & & & & & & & - 7x & + & 14 \\ \hhline{~~~~~~~---} & & & & & & & & & 0 \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c597450232d68b0d21d80f4f1fe0a356_l3.png)
Next, observe that the terms ![]() ,
, ![]() and
and ![]() are the exact opposite of the terms above them. The algorithm we use ensures this is always the case, so we can omit them without losing any information. Also note that the terms we `bring down’ (namely the
are the exact opposite of the terms above them. The algorithm we use ensures this is always the case, so we can omit them without losing any information. Also note that the terms we `bring down’ (namely the ![]() and
and ![]() ) aren’t really necessary to recopy, so we omit them, too.
) aren’t really necessary to recopy, so we omit them, too.
![Rendered by QuickLaTeX.com \[ \begin{array}{cccccccccc} & & & & & x^2 & + & 6x & + & 7 \\ \hhline{~~~|-------} x & - & 2 \, \vline& \, \, x^3 & + & 4x^2 & - & 5x & - & 14 \\ & & & & & 2x^2 & & & & \\ \hhline{~~~---~~~~} & & & & & 6 x^2 & & & & \\ & & & & & & & 12x & & \\ \hhline{~~~~~---~~} & & & & & & & 7x & & \\ & & & & & & & & & 14 \\ \hhline{~~~~~~~---} & & & & & & & & & 0 \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a17fcc15b0b19f26e20149b2037c5908_l3.png)
Let’s move terms up a bit and copy the ![]() into the last row.
into the last row.
![Rendered by QuickLaTeX.com \[ \begin{array}{cccccccccc} & & & & & x^2 & + & 6x & + & 7 \\ \hhline{~~~|-------} x & - & 2 \, \vline& \, \, x^3 & + & 4x^2 & - & 5x & - & 14 \\ & & & & & 2x^2 & & 12x & & 14 \\ \hhline{~~~-------} & & & x^3 & & 6 x^2 & & 7x & &0 \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-58c26c69ed12213221b9e9b423719a5c_l3.png)
Note that by arranging things in this manner, each term in the last row is obtained by adding the two terms above it. Notice also that the quotient polynomial can be obtained by dividing each of the first three terms in the last row by ![]() and adding the results.
and adding the results.
2.3.1 Section Exercises
In Exercises 1 – 12, perform the indicated division. Check your answer by showing
![]()
In Exercises 13 – 26, use long division to perform the following polynomial divisions. Identify the quotient and remainder. Write the dividend, quotient and remainder in the form given in Theorem 2.8.
In Exercises 27 – 36, you are given a polynomial function and one of its zeros. Use long division to compute the quotient, then factor the quotient to determine the remaining real zeros, if possible.
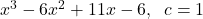
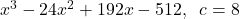
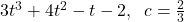
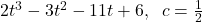
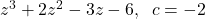
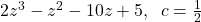
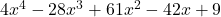 ,
, 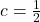 is a zero of multiplicity 2
is a zero of multiplicity 2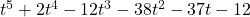 ,
, 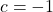 is a zero of multiplicity 3
is a zero of multiplicity 3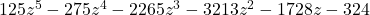 ,
, 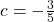 is a zero of multiplicity 3
is a zero of multiplicity 3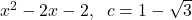
Section 2.3 Exercise Answers can be found in the Appendix … Coming soon

