3.3 Graphs of Rational Functions
In Section 3.2, we learned about the types of behaviors to expect from graphs of rational functions: vertical asymptotes, holes in graph, horizontal and slant asymptotes. Moreover, Theorems 3.2, 3.3, and 3.4 tell us exactly when and where these behaviors will occur. We used rough sketches extensively in the last section to help us verify results. In this section, we delve more deeply into graphing rational functions with the goal of sketching relatively accurate graphs without the aid of a graphing utility. Your instructor will ultimately communicate the level of detail expected out of you when it comes to producing graphs of rational functions; what we provide here is an attempt to glean as much information about the graph as possible given the analytical tools at our disposal.
One of the standard tools we will use is the sign diagram which was first introduced in Section 1.5.1, and then revisited in Section 2.1. In these sections, to construct a sign diagram for a function ![]() , we first found the zeros of
, we first found the zeros of ![]() . The zeros broke the domain of
. The zeros broke the domain of ![]() into a series of intervals. We determined the sign of
into a series of intervals. We determined the sign of ![]() over the entire interval by finding the sign of
over the entire interval by finding the sign of ![]() for just one test value per interval. The theorem that justified this approach was the Intermediate Value Theorem, which says that continuous functions cannot change their sign between two values unless there is a zero between those two values.
for just one test value per interval. The theorem that justified this approach was the Intermediate Value Theorem, which says that continuous functions cannot change their sign between two values unless there is a zero between those two values.
This strategy fails in general with rational functions. Indeed, the very first function we studied in Section 3.2, ![]() changes sign between
changes sign between ![]() and
and ![]() , but there is no zero between these two values – instead, the graph changes sign across a vertical asymptote. We could also well imagine the graph of a rational function having a hole where an
, but there is no zero between these two values – instead, the graph changes sign across a vertical asymptote. We could also well imagine the graph of a rational function having a hole where an ![]() -intercept should be.[1] It turns out that with Calculus we can show rational functions are continuous on their domains. What this means for us is when we construct sign diagrams, we need to choose test values on either side of values excluded from the domain in addition to checking around zeros.[2]
-intercept should be.[1] It turns out that with Calculus we can show rational functions are continuous on their domains. What this means for us is when we construct sign diagrams, we need to choose test values on either side of values excluded from the domain in addition to checking around zeros.[2]
Steps for Constructing a Sign Diagram for a Rational Function
Suppose ![]() is a rational function.
is a rational function.
- Determine the domain of
 .
. - Identify holes and vertical asymptotes for the graph of
 . Indicate any holes in the graph by placing them on the number line with a capital H above them and any vertical asymptotes with a vertical dashed line above them.
. Indicate any holes in the graph by placing them on the number line with a capital H above them and any vertical asymptotes with a vertical dashed line above them. - Determine the zeros of
 and place them on the number line with the number
and place them on the number line with the number  above them.
above them. - Choose a test value in each of the intervals determined in steps 1 and 2.
- Determine and record the sign of
 for each test value in step 3.
for each test value in step 3.
We now present our procedure for graphing rational functions and apply it to a few exhaustive examples. Please note that we decrease the amount of detail given in the explanations as we move through the examples. The reader should be able to fill in any details in those steps which we have abbreviated.
Steps for Graphing Rational Functions
Suppose ![]() is a rational function.
is a rational function.
- Determine the domain of
 .
. - Reduce
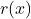 to lowest terms, if applicable.
to lowest terms, if applicable. - Determine the location of any vertical asymptotes or holes in the graph, if they exist.
- Identify the axis intercepts, if they exist.
- Analyze the end behavior of
 . Find the horizontal or slant asymptote, if one exists.
. Find the horizontal or slant asymptote, if one exists. - Use a sign diagram and plot additional points, as needed, to sketch the graph.[3]
Example 3.3.1
Example 3.3.1
Sketch a detailed graph of ![]() .
.
Solution:
We follow the six step procedure outlined above.
- Determine the domain.
To find the domain, we first find the excluded values. To that end, we solve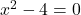 and find
and find 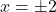 .
.
Our domain is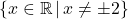 , or, using interval notation,
, or, using interval notation, 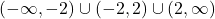 .
. - Reduce
 to lowest terms.
to lowest terms.
We check if is in lowest terms by factoring:
is in lowest terms by factoring:
![Rendered by QuickLaTeX.com \[f(x) = \frac{3x}{(x-2)(x+2)}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-daed22dd1f10326da25370aad28f1d42_l3.png)
There are no common factors which means
 is already in lowest terms.
is already in lowest terms. - Determine the location of any vertical asymptotes or holes in the graph, if they exist.
Per Theorem 3.2, vertical asymptotes and holes in the graph come from values excluded from the domain of .
.
The two numbers excluded from the domain of are
are 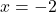 and
and 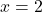 ,
,  didn’t reduce, thus Theorem 3.2 tells us
didn’t reduce, thus Theorem 3.2 tells us 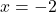 and
and 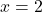 are vertical asymptotes of the graph.
are vertical asymptotes of the graph.
We can actually go a step further at this point and determine exactly how the graph approaches the asymptote near each of these values. Though not absolutely necessary,[4] it is good practice for those heading off to Calculus. For the discussion that follows, we use the factored form of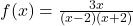 .
.
- The behavior of
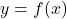 as
as 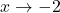 : Suppose
: Suppose 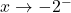 . If we were to build a table of values, we’d use
. If we were to build a table of values, we’d use  -values a little less than
-values a little less than 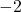 , say
, say 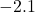 ,
, 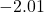 and
and 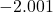 . While there is no harm in actually building a table like we did in Section 3.2, we want to develop a `number sense’ here. Let’s think about each factor in the formula of
. While there is no harm in actually building a table like we did in Section 3.2, we want to develop a `number sense’ here. Let’s think about each factor in the formula of  as we imagine substituting a number like
as we imagine substituting a number like 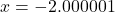 into
into  . The quantity
. The quantity 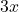 would be very close to
would be very close to 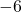 , the quantity
, the quantity 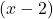 would be very close to
would be very close to 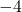 , and the factor
, and the factor 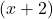 would be very close to
would be very close to  . More specifically,
. More specifically, 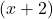 would be a little less than
would be a little less than  , in this case,
, in this case, 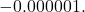 We will call such a number a `very small
We will call such a number a `very small  ‘, `very small’ meaning close to zero in absolute value. So, mentally, as
‘, `very small’ meaning close to zero in absolute value. So, mentally, as 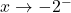 ,
,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f(x) &=& \dfrac{3x}{(x-2)(x+2)} \\[8pt] &\approx& \dfrac{-6}{(-4)\left( \text{very small } (-)\right)} \\[8pt] &=& \dfrac{3}{2 \left( \text{very small } (-)\right)} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-75d212b049226b6f6580783b2b8e4915_l3.png)
Now, the closer
 gets to
gets to 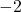 , the smaller
, the smaller 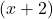 will become, so even though we are multiplying our `very small
will become, so even though we are multiplying our `very small 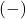 ‘ by
‘ by 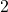 , the denominator will continue to get smaller and smaller, and remain negative. The result is a fraction whose numerator is positive, but whose denominator is very small and negative. Mentally,
, the denominator will continue to get smaller and smaller, and remain negative. The result is a fraction whose numerator is positive, but whose denominator is very small and negative. Mentally,![Rendered by QuickLaTeX.com \[\begin{array}{rcl} f(x) &\approx& \dfrac{3}{2 \left( \text{very small } (-)\right)} \\[8pt] &\approx& \dfrac{3}{\text{very small } (-)} \\[8pt] &\approx& \text{very big } (-) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f3e49d7096a8db8991027a45f03b2f30_l3.png)
The term `very big
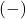 ‘ means a number with a large absolute value which is negative.[5]
‘ means a number with a large absolute value which is negative.[5]
What all of this means is that as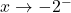 ,
, 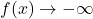 .
.
Now suppose we wanted to determine the behavior of as
as 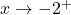 . If we imagine substituting something a little larger than
. If we imagine substituting something a little larger than 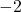 in for
in for  , say
, say 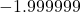 , we mentally estimate
, we mentally estimate![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f(x) &\approx& \dfrac{-6}{(-4)\left( \text{very small } (+) \right)} \\[8pt] &=& \dfrac{3}{2 \left( \text{very small } (+) \right)} \\[8pt] &\approx& \dfrac{3}{\text{very small } (+)} \\[8pt] &\approx & \text{very big } (+) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-90dc7dc6497078d7195736c9a075dc72_l3.png)
We conclude that as
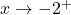 ,
, 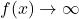 .
. - The behavior of
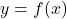 as
as 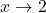 : Consider
: Consider 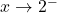 . We imagine substituting
. We imagine substituting 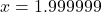 . Approximating
. Approximating  as we did above, we get
as we did above, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f(x) & \approx & \dfrac{6}{\left( \text{very small } (-) \right)(4)} \\[8pt] &=& \dfrac{3}{2 \left( \text{very small } (-) \right)} \\[8pt] &\approx & \dfrac{3}{\text{very small } (-)} \\[8pt] &\approx & \text{very big } (-) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5ba4c2874578f29ba7f41d2bd2c62d4e_l3.png)
We conclude that as
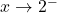 ,
, 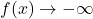 .
.
Similarly, as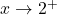 , we imagine substituting
, we imagine substituting 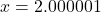 to get
to get![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f(x) & \approx & \frac{3}{\text{\scriptsize very small } (+)} \\[8pt] &\approx & \text{very big } (+) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a9c1f3682d9ea6ff05ad8ca71ea00aff_l3.png)
So as
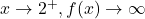 .
.
We interpret this graphically below.
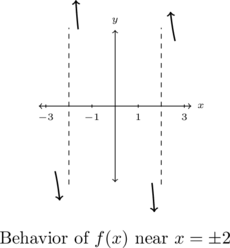
- The behavior of
- Identify the axis intercepts, if they exist.
To find the -intercepts of the graph, we set
-intercepts of the graph, we set 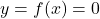 . Solving
. Solving 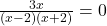 results in
results in 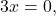 thus
thus 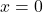 . Because
. Because 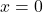 is in our domain,
is in our domain, 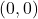 is the
is the  -intercept.
-intercept.
This is also the -intercept,[6] as we can quickly verify with
-intercept,[6] as we can quickly verify with 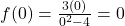 .
. - Analyze the end behavior of
 . Find the horizontal or slant asymptote, if one exists.Next, we determine the end behavior of the graph of
. Find the horizontal or slant asymptote, if one exists.Next, we determine the end behavior of the graph of 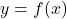 . The degree of the numerator is
. The degree of the numerator is 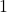 , and the degree of the denominator is
, and the degree of the denominator is 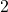 , and so Theorem 3.3 tells us that
, and so Theorem 3.3 tells us that 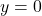 is the horizontal asymptote. As with the vertical asymptotes, we can glean more detailed information using `number sense’. For the discussion below, we use the formula
is the horizontal asymptote. As with the vertical asymptotes, we can glean more detailed information using `number sense’. For the discussion below, we use the formula 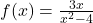 .
.
- The behavior of
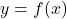 as
as 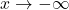 : If we were to make a table of values to discuss the behavior of
: If we were to make a table of values to discuss the behavior of  as
as 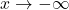 , we would substitute very `large’ negative numbers in for
, we would substitute very `large’ negative numbers in for  , say for example,
, say for example, 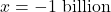 . The numerator
. The numerator 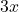 would then be
would then be 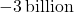 , whereas the denominator
, whereas the denominator 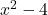 would be
would be 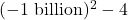 , which is pretty much the same as
, which is pretty much the same as 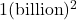 . Hence,
. Hence,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f\left( -1 \text{ billion}\right) &\approx& \dfrac{-3 \text{ billion}}{1(\text{billion})^2} \\[8pt] &\approx& - \dfrac{3}{\text{billion}} \\[8pt] &\approx& \text{very small } (-) \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-669190aea1607706f31bcec15f2e60e8_l3.png)
Notice that if we substituted in
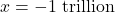 , essentially the same kind of division would occur, and we would be left with an even `smaller’ negative number. This not only confirms the fact that as
, essentially the same kind of division would occur, and we would be left with an even `smaller’ negative number. This not only confirms the fact that as 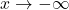 ,
, 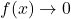 , it tells us that
, it tells us that 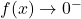 .
.
In other words, the graph of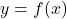 is a little bit below the
is a little bit below the  -axis as we move to the far left.
-axis as we move to the far left. - The behavior of
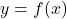 as
as 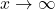 : On the flip side, we can imagine substituting very large positive numbers in for
: On the flip side, we can imagine substituting very large positive numbers in for  and looking at the behavior of
and looking at the behavior of  . For example, let
. For example, let 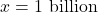 . Proceeding as before, we get
. Proceeding as before, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f\left(\text{1 billion}\right) &\approx& \dfrac{3 \, \text{billion}}{1(\text{billion})^2} \\[8pt] &\approx & \dfrac{3}{\text{billion}} \\[8pt] &\approx& \text{very small } (+) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9e469fed4d3cba7144663dba99d901de_l3.png)
The larger the number we put in, the smaller the positive number we would get out. In other words, as
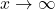 ,
, 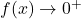 , so the graph of
, so the graph of 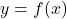 is a little bit above the
is a little bit above the  -axis as we look toward the far right.
-axis as we look toward the far right.
We interpret these findings graphically below.

- The behavior of
- Use a sign diagram and plot additional points, as needed, to sketch the graph.
Lastly, we construct a sign diagram for . The
. The  -values excluded from the domain of
-values excluded from the domain of  are
are 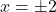 , and the only zero of
, and the only zero of  is
is 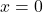 .
.
Displaying these appropriately on the number line gives us four test intervals, and we choose the test values[7]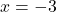 ,
, 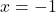 ,
, 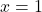 and
and 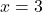 . We find
. We find 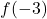 is
is 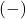 ,
, 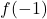 is
is 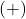 ,
, 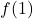 is
is 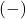 and
and 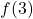 is
is 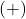 .
.
As we begin our sketch, it certainly appears as if the graph could be symmetric about the origin. Taking a moment to check for symmetry, we find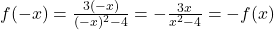 . Hence,
. Hence,  is odd and the graph of
is odd and the graph of  is symmetric about the origin.
is symmetric about the origin.
Putting all of our work together, we get the graph below.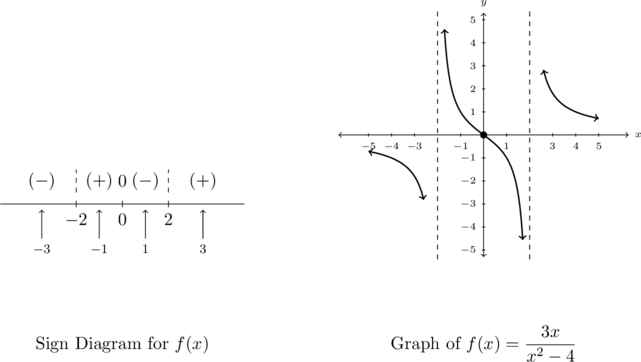
Something important to note about the above example is that while ![]() is the horizontal asymptote, the graph of
is the horizontal asymptote, the graph of ![]() actually crosses the
actually crosses the ![]() -axis at
-axis at ![]() . The myth that graphs of rational functions can’t cross their horizontal asymptotes is completely false,[8] as we shall see again in our next example.
. The myth that graphs of rational functions can’t cross their horizontal asymptotes is completely false,[8] as we shall see again in our next example.
Example 3.3.2
Example 3.3.2
Sketch a detailed graph of ![]() .
.
Solution:
- Determine the domain.
To find the values excluded from the domain of , we solve
, we solve  and find
and find 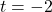 and
and 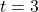 .
.
Hence, our domain is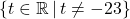 , or using interval notation:
, or using interval notation: 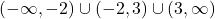 .
. - Reduce
 to lowest terms.
to lowest terms.
To check if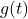 is in lowest terms, we factor:
is in lowest terms, we factor:
![Rendered by QuickLaTeX.com \[g(t) = \frac{(2t-5)(t+1)}{(t-3)(t+2)}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b6504986b1e9caf04cb2eec46b6fb60e_l3.png)
There is no cancellation, so
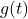 is in lowest terms.
is in lowest terms. - Determine the location of any vertical asymptotes or holes in the graph, if they exist.
Due to the fact that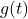 was given to us in lowest terms, we have, once again by Theorem 3.2 vertical asymptotes
was given to us in lowest terms, we have, once again by Theorem 3.2 vertical asymptotes 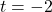 and
and 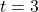 .
.
Keeping in mind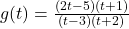 , we proceed to our analysis near each of these values.
, we proceed to our analysis near each of these values.
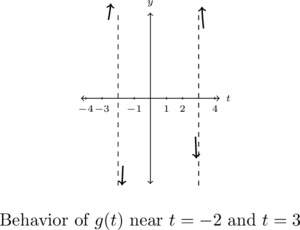
- The behavior of
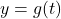 as
as 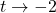 :} As
:} As 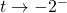 , we imagine substituting a number a little bit less than
, we imagine substituting a number a little bit less than 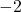 . We have
. We have
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(t) &\approx& \frac{(-9)(-1)}{(-5)(\text{very small } (-))} \\[8pt] &\approx& \frac{9}{\text{very small } (+)} \\[8pt] &\approx& \text{very big } (+) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-ea7cd3701fb92bbca6e386628bb578a3_l3.png)
so as
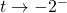 ,
, 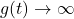 .
.
On the flip side, as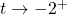 , we get
, we get ![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(t) &\approx& \frac{9}{\text{ very small } (-)} \\[8pt] &\approx & \text{very big } (-) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d1a08ef726f20582b9faaa9ee1a9a8e9_l3.png)
so as
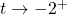 ,
, 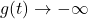 .
. - The behavior of
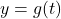 as
as 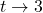 : As
: As 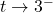 , we imagine plugging in a number just shy of
, we imagine plugging in a number just shy of 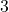 . We have
. We have
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(t) &\approx & \frac{(1)(4)}{(\text{ very small } (-)) (5)} \\[8pt] &\approx & \frac{4}{\text{very small } (-)} \\[8pt] &\approx & \text{very big } (-) \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-af87084ce0dc574ed02ccf26b592aaac_l3.png)
Hence, as
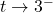 ,
, 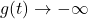 .
.
As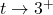 , we get
, we get ![Rendered by QuickLaTeX.com \[\begin{array}{rcl} g(t) &\approx& \frac{4}{\text{ very small } (+)} \\[8pt] &\approx& \text{very big } (+) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-81eee7198428be9f34dc7c8c70b38692_l3.png)
so as
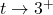 ,
, 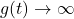 .
.
We interpret this analysis graphically below.
- The behavior of
- Identify the axis intercepts, if they exist.
To find the -intercepts we set
-intercepts we set 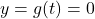 . Using the factored form of
. Using the factored form of 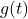 above, we find the zeros to be the solutions of
above, we find the zeros to be the solutions of 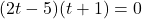 . We obtain
. We obtain 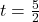 and
and 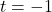 . Both of these numbers are in the domain of
. Both of these numbers are in the domain of  , therefore we have two
, therefore we have two  -intercepts,
-intercepts, 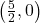 and
and 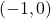 .
.
To find the -intercept, we find
-intercept, we find 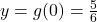 , so our
, so our  -intercept is
-intercept is 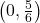 .
. - Analyze the end behavior of
 . Find the horizontal or slant asymptote, if one exists.
. Find the horizontal or slant asymptote, if one exists.
As the degrees of the numerator and denominator of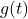 are the same, we know from Theorem 3.3 that we can find the horizontal asymptote of the graph of
are the same, we know from Theorem 3.3 that we can find the horizontal asymptote of the graph of  by taking the ratio of the leading terms coefficients,
by taking the ratio of the leading terms coefficients, 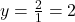 .
.
However, if we take the time to do a more detailed analysis, we will be able to reveal some `hidden’ behavior which would be lost otherwise. Using long division, we may rewrite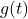 as
as 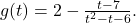 We focus our attention on the term
We focus our attention on the term 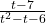 .
.
- The behavior of
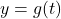 as
as 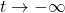 : If imagine substituting
: If imagine substituting 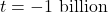 into
into 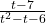 , we estimate
, we estimate
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \frac{t-7}{t^2-t-6} &\approx& \frac{-1 \text{\scriptsize billion}}{1 \text{\scriptsize billion}^2} \\[8pt] &=& \frac{-1}{\text{\scriptsize billion}} \\[8pt] &\approx& \text{very small } (-) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-45d8f7953e7821211887127d646ed54c_l3.png)
[9]
Hence,![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(t) &=& 2 - \frac{t-7}{t^2-t-6} \\[8pt] &\approx & 2 - \text{very small } (-) \\ &=& 2 + \text{very small } (+) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-1489a6b2e786cb624cccafac301c88c5_l3.png)
Hence, as
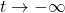 , the graph is a little bit above the line
, the graph is a little bit above the line 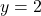 .
. - The behavior of
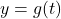 as
as 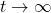 . To consider
. To consider 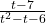 as
as 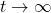 , we imagine substituting
, we imagine substituting 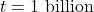 and, going through the usual mental routine, find
and, going through the usual mental routine, find
![Rendered by QuickLaTeX.com \[\frac{t-7}{t^2-t-6} \approx \text{very small } (+) \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-43c0884f49661ce9293a70c8bfb14325_l3.png)
Hence,
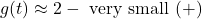 , so the graph is just below the line
, so the graph is just below the line 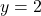 as
as 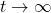 .
.
- The behavior of
We sketch the end behavior below.

- Use a sign diagram and plot additional points, as needed, to sketch the graph.
Finally we construct our sign diagram. We place an dashed line above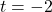 and
and 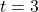 , and a `
, and a ` ‘ above
‘ above 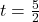 and
and 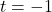 .Choosing test values in the test intervals gives us
.Choosing test values in the test intervals gives us 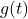 is
is 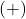 on the intervals
on the intervals 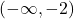 ,
, 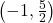 and
and 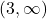 , and
, and 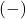 on the intervals
on the intervals 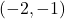 and
and 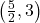 .As we piece together all of the information, it stands to reason the graph must cross the horizontal asymptote at some point after
.As we piece together all of the information, it stands to reason the graph must cross the horizontal asymptote at some point after 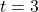 in order for it to approach
in order for it to approach 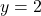 from underneath.[10]To find where
from underneath.[10]To find where 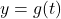 intersects
intersects 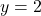 , we solve
, we solve 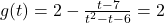 and get
and get 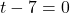 , or
, or 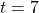 . Note that
. Note that 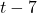 is the remainder when
is the remainder when 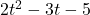 is divided by
is divided by 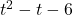 , so it makes sense that for
, so it makes sense that for 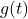 to equal the quotient
to equal the quotient 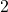 , the remainder from the division must be
, the remainder from the division must be  . Sure enough, we find
. Sure enough, we find 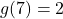 .The location of the
.The location of the  -intercepts alone dashes all hope of the function being even or odd (do you see why?) so we skip the symmetry check in this case.
-intercepts alone dashes all hope of the function being even or odd (do you see why?) so we skip the symmetry check in this case.
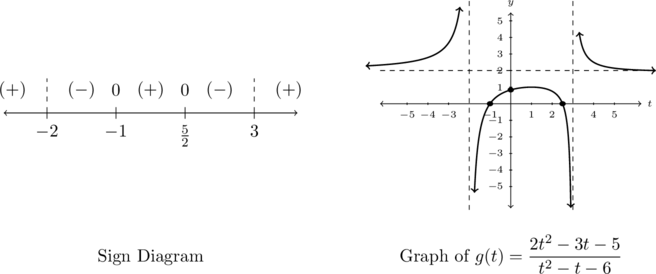
More can be said about the graph of ![]() . It stands to reason that
. It stands to reason that ![]() must attain a local minimum at some point past
must attain a local minimum at some point past ![]() because the graph of
because the graph of ![]() crosses through
crosses through ![]() at
at ![]() but approaches
but approaches ![]() from below as
from below as ![]() . Calculus verifies a local minimum at
. Calculus verifies a local minimum at ![]() . We invite the reader to verify this claim using a graphing utility.
. We invite the reader to verify this claim using a graphing utility.
Example 3.3.3
Example 3.3.3
Sketch a detailed graph of ![]() .
.
Solution:
- Determine the domain.
Solving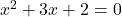 gives
gives 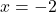 and
and 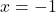 as our excluded values.
as our excluded values.
Hence, the domain is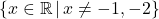 or, using interval notation,
or, using interval notation, 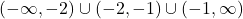 .
. - Reduce
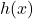 to lowest terms.
to lowest terms.
To reduce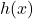 , we need to factor the numerator and denominator. To factor the numerator, we use the techniques[11] set forth in Section 0.3 and get
, we need to factor the numerator and denominator. To factor the numerator, we use the techniques[11] set forth in Section 0.3 and get
![Rendered by QuickLaTeX.com \[\begin{array}{rcl} h(x) &=& \dfrac{2x^3+5x^2+4x+1}{x^2+3x+2} \\[10pt] &=& \dfrac{(2x+1)(x+1)^2}{(x+2)(x+1)} \\[8pt] &=& \dfrac{ (2x+1) (x+1)^{\cancelto{1}{2}} }{(x+2)\cancel{(x+1)}} \\[10pt] &=& \dfrac{(2x+1)(x+1)}{x+2}\end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b7ea4f53ccc8427819a05b2a6c954d0e_l3.png)
Note we can use this formula for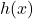 in our analysis of the graph of
in our analysis of the graph of  as long as we are not substituting
as long as we are not substituting 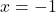 . To make this exclusion specific, we write
. To make this exclusion specific, we write
![Rendered by QuickLaTeX.com \[ h(x) = \dfrac{(2x+1)(x+1)}{x+2}, \; \; x \neq -1 \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9b6c8a9a94df64d6f12051a174aad76e_l3.png)
- Determine the location of any vertical asymptotes or holes in the graph, if they exist.
From Theorem 3.2, we know that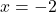 is a zero of the denominator of the reduced form of
is a zero of the denominator of the reduced form of 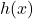 , thus we have a vertical asymptote there.
, thus we have a vertical asymptote there.
As for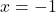 , the factor
, the factor 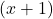 was divided from the denominator when we reduced
was divided from the denominator when we reduced 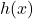 , so there will be a hole when
, so there will be a hole when 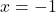 . To find the
. To find the  -coordinate of the hole, we substitute
-coordinate of the hole, we substitute 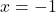 into
into 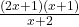 , per Theorem 3.2 and get
, per Theorem 3.2 and get  . Hence, we have a hole on the
. Hence, we have a hole on the  -axis at
-axis at 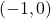 .It should make you uncomfortable plugging
.It should make you uncomfortable plugging 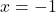 into the reduced formula for
into the reduced formula for 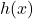 , especially because we’ve made such a big deal about the stipulation `
, especially because we’ve made such a big deal about the stipulation `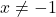 ‘ that goes along with that formula. What we are really doing is taking a Calculus short-cut to the more detailed kind of analysis near
‘ that goes along with that formula. What we are really doing is taking a Calculus short-cut to the more detailed kind of analysis near 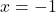 which we will show below.
which we will show below.
- The behavior of
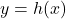 as
as 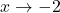 : As
: As 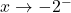 , we imagine substituting a number a little bit less than
, we imagine substituting a number a little bit less than 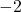 . We have
. We have
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} h(x) &\approx & \frac{(-3)(-1)}{(\text{\scriptsize very small } (-))} \\[8pt] &\approx & \frac{3}{(\text{\scriptsize very small } (-))} \\[8pt] &\approx & \text{very big } (-) \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e33b12150ce9f2e5e875a7552f818fd4_l3.png)
thus as
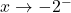 ,
, 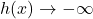 .
.
On the other side of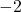 , as
, as 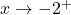 , we find that
, we find that![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} h(x) &\approx & \frac{3}{\text{ very small } (+)} \\[8pt] &\approx & \text{very big } (+) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4c71d396175ee4937487d5231566358b_l3.png)
so
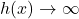 .
. - The behavior of
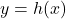 as
as 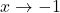 : As
: As 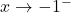 , we imagine plugging in a number a bit less than
, we imagine plugging in a number a bit less than 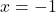 . We have
. We have
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} h(x) &\approx & \frac{(-1)(\text{ very small } (-))}{1} \\[8pt] &=& \text{very small } (+) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-3ab3c09cd8b794bc363f8c5e588b7586_l3.png)
Hence, as
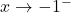 ,
, 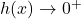 . This means that as
. This means that as 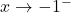 , the graph is a bit above the point
, the graph is a bit above the point 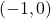 .As
.As 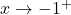 , we get
, we get ![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} h(x) &\approx & \frac{(-1)(\text{\scriptsize very small }(+))}{1} \\[8pt] &=& \text{very small } (-) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7a2391df5a3741b55820c02a48454bb6_l3.png)
This gives us that as
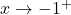 ,
, 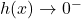 , so the graph is a little bit lower than
, so the graph is a little bit lower than 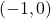 here.
here.
We interpret this graphically below.

- The behavior of
- Identify the axis intercepts, if they exist.
To find the -intercepts, as usual, we set
-intercepts, as usual, we set 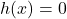 and solve. Solving
and solve. Solving 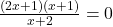 yields
yields 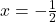 and
and 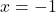 .The latter isn’t in the domain of
.The latter isn’t in the domain of  , in fact, we know there is a hole at
, in fact, we know there is a hole at 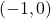 , so we exclude it. Our only
, so we exclude it. Our only  -intercept is
-intercept is 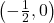 .To find the
.To find the  -intercept, we set
-intercept, we set 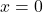 . Due to the fact that
. Due to the fact that 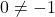 , we can use the reduced formula for
, we can use the reduced formula for 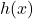 and we get
and we get 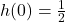 for a
for a  -intercept of
-intercept of 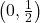 .
. - Analyze the end behavior of
 . Find the horizontal or slant asymptote, if one exists.
. Find the horizontal or slant asymptote, if one exists.
For end behavior, we note that the degree of the numerator of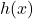 ,
, 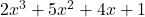 , is
, is 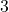 and the degree of the denominator,
and the degree of the denominator, 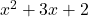 , is
, is 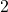 so by Theorem 3.4, the graph of
so by Theorem 3.4, the graph of 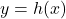 has a slant asymptote.
has a slant asymptote.
For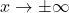 , we are far enough away from
, we are far enough away from 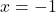 to use the reduced formula,
to use the reduced formula, 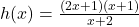 ,
, 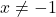 .To perform long division, we multiply out the numerator and get
.To perform long division, we multiply out the numerator and get 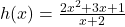 ,
, 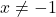 , and rewrite
, and rewrite 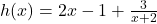 ,
, 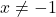 .By Theorem 3.4, the slant asymptote is
.By Theorem 3.4, the slant asymptote is 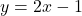 , and to better see how the graph approaches the asymptote, we focus our attention on the term generated from the remainder,
, and to better see how the graph approaches the asymptote, we focus our attention on the term generated from the remainder, 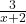 .
.
- The behavior of
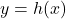 as
as 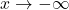 : Substituting
: Substituting 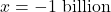 into
into 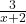 , we get the estimate
, we get the estimate
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \frac{3}{-1 \text{\scriptsize billion}} &\approx& \text{very small } (-) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-95f9a308c60a11bce4c2f5585d148e66_l3.png)
Hence,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} h(x) &=& 2x-1+\frac{3}{x+2} \\[8pt] &\approx& 2x-1 + \text{very small } (-) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4f701e515aa577104509c4772a2f65dc_l3.png)
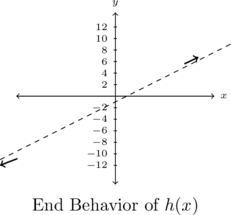
This means the graph of
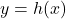 is a little bit below the line
is a little bit below the line 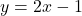 as
as 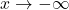 .
. - The behavior of
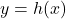 as
as 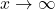 : If
: If 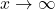 , then
, then
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \frac{3}{x+2} &\approx& \text{very small } (+) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-dfb5b20ecd486dce447061241daf05ca_l3.png)
This means
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} h(x) &\approx& 2x-1 + \text{very small } (+) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7c07fb2809be0e53205a568334f9f411_l3.png)
or that the graph of
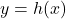 is a little bit above the line
is a little bit above the line 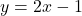 as
as 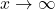 .
.
We sketch the end behavior below.
- The behavior of
- Use a sign diagram and plot additional points, as needed, to sketch the graph.
To make our sign diagram, we place a dashed line above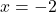 and an `H’ above
and an `H’ above 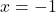 and a `
and a ` ‘ above
‘ above 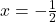 .On our four test intervals, we find
.On our four test intervals, we find 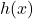 is
is 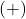 on
on 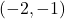 and
and 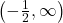 and
and 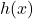 is
is 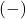 on
on 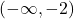 and
and 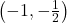 .Putting all of our work together yields the graph below.
.Putting all of our work together yields the graph below.

To find if the graph of
 ever crosses the slant asymptote, we solve
ever crosses the slant asymptote, we solve 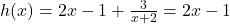 . This results in
. This results in 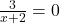 , which has no solution.[12] Hence, the graph of
, which has no solution.[12] Hence, the graph of  never crosses its slant asymptote.[13]
never crosses its slant asymptote.[13]
Our last graphing example is challenging in that our six step process provides us little information to work with.
Example 3.3.4
Example 3.3.4
Sketch a detailed graph of ![]() .
.
Solution:
- Determine the domain.
The denominator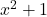 is never zero which means there are no excluded values.The domain is
is never zero which means there are no excluded values.The domain is 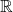 , or using interval notation,
, or using interval notation,  .
. - Reduce
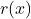 to lowest terms. <br>With no real zeros in the denominator,
to lowest terms. <br>With no real zeros in the denominator, 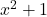 is an irreducible quadratic. Our only hope of reducing
is an irreducible quadratic. Our only hope of reducing 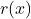 is if
is if 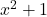 is a factor of
is a factor of 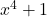 . Performing long division gives us
. Performing long division gives us
![Rendered by QuickLaTeX.com \[\frac{x^4+1}{x^2+1} = x^2-1+\frac{2}{x^2+1}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-dce2cf08e7b1ad420a3db6a235d6d0cf_l3.png)
The remainder is not zero so
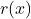 is already reduced.
is already reduced. - Determine the location of any vertical asymptotes or holes in the graph, if they exist. <br>There are no numbers excluded from the domain of
 , so there are no vertical asymptotes or holes in the graph of
, so there are no vertical asymptotes or holes in the graph of  .
. - Identify the axis intercepts, if they exist. <br>To find the
 -intercept, we’d set
-intercept, we’d set 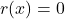 . As there are no real solutions to
. As there are no real solutions to 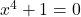 , we have no
, we have no  -intercepts.<br>
-intercepts.<br>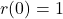 , thus we do get
, thus we do get 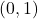 as the
as the  -intercept.
-intercept. - Analyze the end behavior of
 . Find the horizontal or slant asymptote, if one exists.<br>For end behavior, we note that because the degree of the numerator is exactly two more than the degree of the denominator, neither Theorems 3.3 nor 3.4 apply.<br>We know from our attempt to reduce
. Find the horizontal or slant asymptote, if one exists.<br>For end behavior, we note that because the degree of the numerator is exactly two more than the degree of the denominator, neither Theorems 3.3 nor 3.4 apply.<br>We know from our attempt to reduce 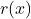 that we can rewrite
that we can rewrite 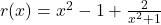 , so we focus our attention on the term corresponding to the remainder,
, so we focus our attention on the term corresponding to the remainder, 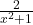 It should be clear that as
It should be clear that as 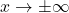 ,
,
![Rendered by QuickLaTeX.com \[ \frac{2}{x^2+1} \approx \text{very small } (+) \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-066b0a110fb9d027fe290755e2a39c19_l3.png)
which means
![Rendered by QuickLaTeX.com \[ r(x) \approx x^2-1 + \text{very small } (+) \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-908b2dbb01367cd737c8cbf53bba0fd4_l3.png)
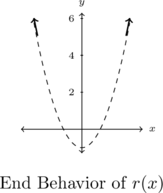
So the graph
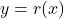 is a little bit above the graph of the parabola
is a little bit above the graph of the parabola 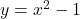 as
as 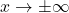 .
.
- Use a sign diagram and plot additional points, as needed, to sketch the graph.<br>There isn’t much work to do for a sign diagram for
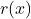 , because its domain is all real numbers and it has no zeros. Our sole test interval is
, because its domain is all real numbers and it has no zeros. Our sole test interval is  , and we know
, and we know 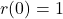 , so we conclude
, so we conclude 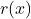 is
is 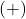 for all real numbers.<br>We check for symmetry, and find
for all real numbers.<br>We check for symmetry, and find 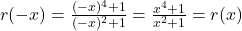 , so
, so  is even and, hence, the graph is symmetric about the
is even and, hence, the graph is symmetric about the  -axis. It may be tempting at this point to call it quits, reach for a graphing utility, or ask someone who knows Calculus.[14] It turns out, we can do a little bit better. Recall from Section 2.2.1, that when
-axis. It may be tempting at this point to call it quits, reach for a graphing utility, or ask someone who knows Calculus.[14] It turns out, we can do a little bit better. Recall from Section 2.2.1, that when 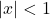 but
but 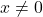 ,
, 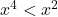 , hence
, hence 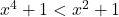 . This means for
. This means for 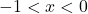 and
and 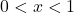 ,
, 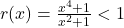 .<br>Because
.<br>Because 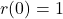 , the graph of
, the graph of 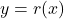 must fall to either side before heading off to
must fall to either side before heading off to 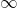 . This means
. This means 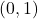 is a local maximum and, moreover, there are at least two local minimums, one on either side of
is a local maximum and, moreover, there are at least two local minimums, one on either side of 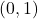 .<br>We invite the reader to confirm this using a graphing utility.
.<br>We invite the reader to confirm this using a graphing utility.
Our last example turns the tables and invites us to write formulas for rational function given their graphs.
Example 3.3.5
Example 3.3.5
Write formulas for rational functions ![]() and
and ![]() given their graphs below:
given their graphs below:
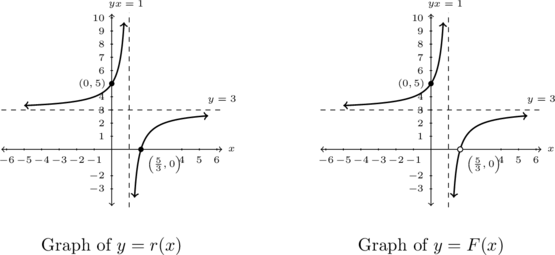
Solution:
The good news is the graph of ![]() closely resembles the graph of
closely resembles the graph of ![]() , so once we know an expression for
, so once we know an expression for ![]() , we should be able to modify it to obtain
, we should be able to modify it to obtain ![]() .
.
We are told ![]() is a rational function, so we know there are polynomial functions
is a rational function, so we know there are polynomial functions ![]() and
and ![]() so that
so that ![]() . We can factor
. We can factor ![]() and
and ![]() completely in terms of their leading coefficients and their zeros. For simplicity’s sake, we assume neither
completely in terms of their leading coefficients and their zeros. For simplicity’s sake, we assume neither ![]() nor
nor ![]() has any non-real zeros.
has any non-real zeros.
We focus our attention first on finding an expression for ![]() . When finding the
. When finding the ![]() -intercepts, we look for the zeros of
-intercepts, we look for the zeros of ![]() by solving
by solving ![]() . This equation quickly reduces to solving
. This equation quickly reduces to solving ![]() .
.
As ![]() is an
is an ![]() -intercept of the graph, we know
-intercept of the graph, we know ![]() is a zero of
is a zero of ![]() , and, hence, a zero of
, and, hence, a zero of ![]() . Due to the fact that we are shown no other
. Due to the fact that we are shown no other ![]() -intercepts, we assume
-intercepts, we assume ![]() , hence
, hence ![]() , have no other real zeros (and no non-real zeros by our assumption.) Definition 2.9 gives
, have no other real zeros (and no non-real zeros by our assumption.) Definition 2.9 gives ![]() where
where ![]() is the leading coefficient of
is the leading coefficient of ![]() and
and ![]() is the multiplicity of the zero
is the multiplicity of the zero ![]() . The graph of
. The graph of ![]() crosses through the
crosses through the ![]() -axis in what appears to be a fairly linear fashion at
-axis in what appears to be a fairly linear fashion at ![]() , so it seems reasonable to set
, so it seems reasonable to set ![]() . Hence,
. Hence, ![]() .
.
Next, we focus our attention on finding ![]() . Theorem 3.2 says
. Theorem 3.2 says ![]() comes from a factor of
comes from a factor of ![]() in the denominator of
in the denominator of ![]() . This means
. This means ![]() is a factor of
is a factor of ![]() . Because there are no other vertical asymptotes or holes in the graph,
. Because there are no other vertical asymptotes or holes in the graph, ![]() is the only real zero, hence (per our assumption) the only zero of
is the only real zero, hence (per our assumption) the only zero of ![]() . At this point, we have
. At this point, we have ![]() where
where ![]() is the leading coefficient of
is the leading coefficient of ![]() and
and ![]() is the multiplicity of the zero
is the multiplicity of the zero ![]() . As the graph of
. As the graph of ![]() has the horizontal asymptote
has the horizontal asymptote ![]() ,Theorem 3.4 tells us two things: first, degree of
,Theorem 3.4 tells us two things: first, degree of ![]() must match the degree of
must match the degree of ![]() ; second, the ratio
; second, the ratio ![]() . Hence, the degree of
. Hence, the degree of ![]() is
is ![]() so that:
so that:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} r(x) & = & \dfrac{a \left(x - \frac{5}{3}\right)}{b(x-1)} \\ & = & \dfrac{a}{b} \left(\dfrac{x - \frac{5}{3}}{x-1}\right) \\ & = & 3 \left(\dfrac{x - \frac{5}{3}}{x-1}\right) \\ & = & \dfrac{3x-5}{x-1}. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-dc9fdccf5d3876bd24bbca4fd18e670e_l3.png)
We have yet to use the ![]() -intercept,
-intercept, ![]() . In this case, we use it as a partial check:
. In this case, we use it as a partial check: ![]() , as required. We can sketch
, as required. We can sketch ![]() by hand, to give a better check of our work.
by hand, to give a better check of our work.
Now it is time to find a formula for ![]() . The graphs of
. The graphs of ![]() and
and ![]() look identical except the graph of
look identical except the graph of ![]() has a hole at
has a hole at ![]() instead of an
instead of an ![]() -intercept. Theorem 3.2 tells us this happens because a factor of
-intercept. Theorem 3.2 tells us this happens because a factor of ![]() divides out from the denominator when the formula for
divides out from the denominator when the formula for ![]() is reduced. Hence, we reverse this process and multiply the numerator and denominator of our expression for
is reduced. Hence, we reverse this process and multiply the numerator and denominator of our expression for ![]() by
by ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} F(x) & = & r(x) \cdot \dfrac{\left(x - \frac{5}{3} \right)}{\left(x - \frac{5}{3} \right)} & \\[8pt] & = & \dfrac{3x-5}{x-1} \cdot \dfrac{\left(x - \frac{5}{3} \right)}{\left(x - \frac{5}{3} \right)} & \\[10pt] & = & \dfrac{3x^2-10x+\frac{25}{3}}{x^2 - \frac{8}{3} x + \frac{5}{3}} & \text{expand}\\[10pt] & = & \dfrac{9x^2-30x+25}{3x^2-8x+5} & \text{multiply by } 1 = \frac{3}{3} \text{ to reduce complex fractions.}\\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9899347ba84b84a25295e099b9ae983f_l3.png)
Again, we can check our answer by applying the six step method to this function or, for a quick verification, we can use a graphing utility.[15]
Another way to approach Example 3.3.5 is to take a cue from Theorem 3.1. The graph of ![]() certainly appears to be the result of moving around the graph of
certainly appears to be the result of moving around the graph of ![]() . To that end, suppose
. To that end, suppose ![]() . As the vertical asymptote is
. As the vertical asymptote is ![]() and the horizontal asymptote is
and the horizontal asymptote is ![]() , we get
, we get ![]() and
and ![]() . At this point, we have
. At this point, we have ![]() . We can determine
. We can determine ![]() by using the
by using the ![]() -intercept,
-intercept, ![]() :
: ![]() gives us
gives us ![]() so
so ![]() . Hence,
. Hence, ![]() . At this point we could check the
. At this point we could check the ![]() -intercept
-intercept ![]() is on the graph, check our answer using a graphing utility, or even better, get common denominators and write
is on the graph, check our answer using a graphing utility, or even better, get common denominators and write ![]() as a single rational expression to compare with our answer in the above example.
as a single rational expression to compare with our answer in the above example.
As usual, the authors offer no apologies for what may be construed as `pedantry’ in this section. We feel that the detail presented in this section is necessary to obtain a firm grasp of the concepts presented here and it also serves as an introduction to the methods employed in Calculus. In the end, your instructor will decide how much, if any, of the kinds of details presented here are `mission critical’ to your understanding of Precalculus. Without further delay, we present you with this section’s Exercises.
3.3.1 Section Exercises
In Exercises 1 – 16, use the six-step procedure to graph the rational function. Be sure to draw any asymptotes as dashed lines.
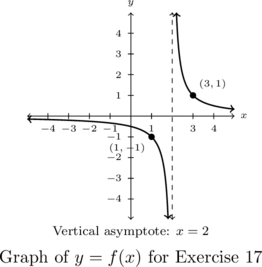
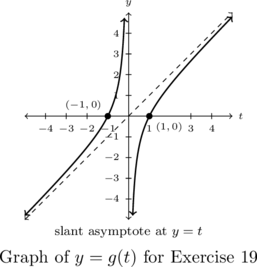
In Exercises 17 – 20, write a possible formula for the function whose graph is given.
Section 3.3 Exercise Answers can be found in the Appendix … Coming soon
- Take
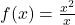 , for instance. ↵
, for instance. ↵ - As excluded values are zeros of the denominator, we can think of this as really just generalizing what we already do. ↵
- It doesn't hurt to check for symmetry at this point, if convenient. ↵
- The sign diagram in step 6 will also determine the behavior near the vertical asymptotes. ↵
- The actual retail value of
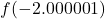 is approximately
is approximately 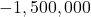 . ↵
. ↵ - Per Exercise 77, functions can have at most one
 -intercept.
-intercept. 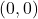 is on the graph, thus it is the
is on the graph, thus it is the  -intercept. ↵
-intercept. ↵ - In this particular case, we don't need test values because our analysis of the behavior of
 near the vertical asymptotes and our end behavior analysis have given us the signs on each of the test intervals. In general, however, this won't always be the case, so for demonstration purposes, we continue with our usual construction. ↵
near the vertical asymptotes and our end behavior analysis have given us the signs on each of the test intervals. In general, however, this won't always be the case, so for demonstration purposes, we continue with our usual construction. ↵ - That's why we called it a MYTH! ↵
- We are once again using the fact that for polynomials, end behavior is determined by the leading term, so in the denominator, the
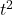 term dominates the
term dominates the  and constant terms. ↵
and constant terms. ↵ - This subtlety would have been missed had we skipped the long division and subsequent end behavior analysis. ↵
- Bet you never thought you'd never see that stuff again before the Final Exam! ↵
- Alternatively, the remainder after the long division was
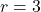 which is never
which is never  . ↵
. ↵ - But rest assured, some graphs do! ↵
- This is exactly what the authors did in the Third Edition. Special thanks go to Erik Boczko from Ohio University for showing us that, in fact, we could do more with this example algebraically. ↵
- Be warned, however, a graphing utility may not show the hole at
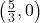 . ↵
. ↵