4.4 Solving Nonlinear Inequalities
4.4.1 Inequalities involving Quadratic Functions
We now turn our attention to solving inequalities involving quadratic functions. Consider the inequality ![]() . We could use the fact that the square root is increasing[1] to get:
. We could use the fact that the square root is increasing[1] to get: ![]() , or
, or ![]() . This reduces to
. This reduces to ![]() or, using interval notation,
or, using interval notation, ![]() . If, however, we had to solve
. If, however, we had to solve ![]() , things are more complicated. One approach is to complete the square:
, things are more complicated. One approach is to complete the square:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} x^2 & \leq & x+6 \\ x^2 - x & \leq & 6 \\ x^2 - x + \frac{1}{4} & \leq & 6 + \frac{1}{4} \\ [3pt] \left(x - \frac{1}{2} \right)^2 & \leq & \frac{25}{4} \\ [3pt] \sqrt{\left(x - \frac{1}{2} \right)^2} & \leq & \sqrt{\frac{25}{4}} \\ [3pt] \left| x - \frac{1}{2} \right| & \leq & \frac{5}{2} \\ -\frac{5}{2} \quad \leq & x - \frac{1}{2} & \leq \quad \frac{5}{2} \\ -2 \quad & \leq x \leq & 3 \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-dc4c4b05c28ec19f1cd2758802fe5a48_l3.png)
We get the solution ![]() . While there is nothing wrong with this approach, we seek methods here that will generalize to higher degree polynomials such as those seen in Chapter 2.
. While there is nothing wrong with this approach, we seek methods here that will generalize to higher degree polynomials such as those seen in Chapter 2.
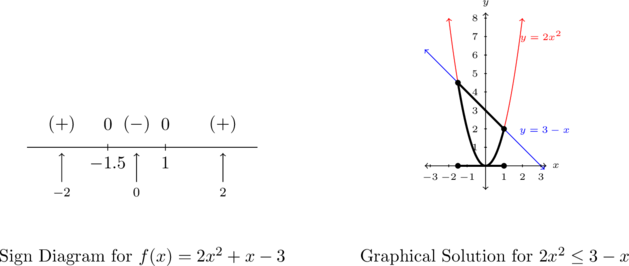
To that end, we look at the inequality ![]() graphically. Identifying
graphically. Identifying ![]() and
and ![]() , we graph
, we graph ![]() and
and ![]() on the same set of axes below on the left and look for where the graph of
on the same set of axes below on the left and look for where the graph of ![]() (the parabola) meets or is below the graph of
(the parabola) meets or is below the graph of ![]() (the line). There are two points of intersection which we determine by solving
(the line). There are two points of intersection which we determine by solving ![]() or
or ![]() . As usual, we rewrite this equation as
. As usual, we rewrite this equation as ![]() in order to use the primary tools we’ve developed to handle these types[2] of quadratic equations: factoring, or failing that, the Quadratic Formula. We find
in order to use the primary tools we’ve developed to handle these types[2] of quadratic equations: factoring, or failing that, the Quadratic Formula. We find ![]() so we get two solutions to
so we get two solutions to ![]() , namely
, namely ![]() and
and ![]() . Putting these together with the graph, we obtain the same solution:
. Putting these together with the graph, we obtain the same solution: ![]() .
.

Yet a third way to attack ![]() is to rewrite the inequality as
is to rewrite the inequality as ![]() . Here, we graph
. Here, we graph ![]() to look for where the graph meets or is below the graph of
to look for where the graph meets or is below the graph of ![]() , a.k.a. the
, a.k.a. the ![]() -axis. Doing so requires us to find the zeros of
-axis. Doing so requires us to find the zeros of ![]() , that is, solve
, that is, solve ![]() from which we obtain
from which we obtain ![]() and
and ![]() as before. We find the same solution,
as before. We find the same solution, ![]() as is showcased in the graph above on the right.
as is showcased in the graph above on the right.
One advantage to using this last approach is that we are essentially concerned with one function and its zeros. This approach can be generalized to all functions – not just quadratics, so we take the time to develop this method more thoroughly now.
Consider the graph of ![]() below. The zeros of
below. The zeros of ![]() are
are ![]() and
and ![]() and they divide the domain (the
and they divide the domain (the ![]() -axis) into three intervals:
-axis) into three intervals: ![]() ,
, ![]() and
and ![]() . For every number in
. For every number in ![]() , the graph of
, the graph of ![]() is above the
is above the ![]() -axis; in other words,
-axis; in other words, ![]() for all
for all ![]() in
in ![]() . Similarly,
. Similarly, ![]() for all
for all ![]() in
in ![]() , and
, and ![]() for all
for all ![]() in
in ![]() . We represent this schematically with the sign diagram below.
. We represent this schematically with the sign diagram below.

The ![]() above a portion of the number line indicates
above a portion of the number line indicates ![]() for those values of
for those values of ![]() and the
and the ![]() indicates
indicates ![]() there. The numbers labeled on the number line are the zeros of
there. The numbers labeled on the number line are the zeros of ![]() , so we place
, so we place ![]() above them. For the inequality
above them. For the inequality ![]() , we read from the sign diagram that the solution is
, we read from the sign diagram that the solution is ![]() .
.
Our next goal is to establish a procedure by which we can generate the sign diagram without graphing the function. While parabolas aren’t that bad to graph knowing what we know, our sights are set on more general functions whose graphs are more complicated.
An important property of parabolas is that a parabola can’t be above the ![]() -axis at one point and below the
-axis at one point and below the ![]() -axis at another point without crossing the
-axis at another point without crossing the ![]() -axis at some point in between. Said differently, if the function is positive at one point and negative at another, the function must have at least one zero in between. This property is a consequence of quadratic functions being continuous. A precise definition of `continuous’ requires the language of Calculus, but it suffices for us to know that the graph of a continuous function has no gaps or holes. This allows us to determine the sign of all of the function values on a given interval by testing the function at just one value in the interval.
-axis at some point in between. Said differently, if the function is positive at one point and negative at another, the function must have at least one zero in between. This property is a consequence of quadratic functions being continuous. A precise definition of `continuous’ requires the language of Calculus, but it suffices for us to know that the graph of a continuous function has no gaps or holes. This allows us to determine the sign of all of the function values on a given interval by testing the function at just one value in the interval.
The result below applies to all continuous functions defined on an interval of real numbers, but we restrict our attention to quadratic functions for the time being,
Steps for Creating A Sign Diagram for A Quadratic Function
Suppose ![]() is a quadratic function.
is a quadratic function.
- Compute the zeros of
 and place them on the number line with the number
and place them on the number line with the number  above them.
above them. - Choose a real number, called a test value, in each of the intervals determined in step 1.
- Determine and record the sign of
 for each test value in step 2.
for each test value in step 2.
To use a sign diagram to solve an inequality, we must always remember to compare the function to ![]() .
.
Solving Inequalities using Sign Diagrams
To solve an inequality using a sign diagram:
- Rewrite the inequality so some function
 is being compared to `
is being compared to ` .’
.’ - Make a sign diagram for
 .
. - Record the solution.
We practice this approach in the following example.
Example 4.4.1
Example 4.4.1.1
Solve the following inequalities analytically[3] and check your solutions graphically.
![]()
Solution:
Solve ![]() .
.
To solve ![]() , we rewrite it as
, we rewrite it as ![]() .
.
We find the zeros of ![]() by solving
by solving ![]() . Factoring gives
. Factoring gives ![]() , so
, so ![]() or
or ![]() .
.
We place these values on the number line with ![]() above them and choose test values in the intervals
above them and choose test values in the intervals ![]() ,
, ![]() and
and ![]() .
.
For the interval ![]() , we choose[4]
, we choose[4] ![]() ; for
; for ![]() , we pick
, we pick ![]() ; and for
; and for ![]() ,
, ![]() .
.
Evaluating the function at the three test values gives us ![]() , so we place
, so we place ![]() above
above ![]() ;
; ![]() , so
, so ![]() goes above the interval
goes above the interval ![]() ; and,
; and, ![]() , which means
, which means ![]() is placed above
is placed above ![]() .
.
We are solving ![]() , so we need solutions to
, so we need solutions to ![]() as well as solutions for
as well as solutions for ![]() . For
. For ![]() , we need the intervals which we have a
, we need the intervals which we have a ![]() above them.
above them.
The sign diagram shows only one: ![]() . Also, we know
. Also, we know ![]() when
when ![]() and
and ![]() , so our final answer is
, so our final answer is ![]() .
.
To verify our solution graphically, we refer to the original inequality, ![]() . We let
. We let ![]() and
and ![]() . We are looking for the
. We are looking for the ![]() values where the graph of
values where the graph of ![]() (in red) is below that of
(in red) is below that of ![]() (in blue) (the solution to
(in blue) (the solution to ![]() ) as well as the points of intersection (the solutions to
) as well as the points of intersection (the solutions to ![]() ). The graphs of
). The graphs of ![]() and
and ![]() are given on the right with the sign chart on the left.
are given on the right with the sign chart on the left.
Example 4.4.1.2
Solve the following inequalities analytically[5] and check your solutions graphically.
![]()
Solution:
Solve ![]() .
.
Once again, we re-write ![]() as
as ![]() and we identify
and we identify ![]() .
.
When we go to find the zeros of ![]() , we find, to our chagrin, that the quadratic
, we find, to our chagrin, that the quadratic ![]() doesn’t factor nicely. Hence, we resort to the Quadratic Formula and find
doesn’t factor nicely. Hence, we resort to the Quadratic Formula and find ![]() .
.
As before, these zeros divide the number line into three pieces. To help us decide on test values, we approximate ![]() and
and ![]() .
.
We choose ![]() ,
, ![]() and
and ![]() as our test values and find
as our test values and find ![]() , which is
, which is ![]() ;
; ![]() which is
which is ![]() ; and
; and ![]() which is
which is ![]() again.
again.
Our solution to ![]() is where we have
is where we have ![]() , so, in interval notation
, so, in interval notation ![]() .
.
To check the inequality ![]() graphically, we set
graphically, we set ![]() and
and ![]() . We are looking for the
. We are looking for the ![]() values where the graph of
values where the graph of ![]() (in red) is above the graph of
(in red) is above the graph of ![]() (in blue). As before we present the graphs on the right and the sign chart on the left.
(in blue). As before we present the graphs on the right and the sign chart on the left.

Example 4.4.1.3
Solve the following inequalities analytically[6] and check your solutions graphically.
![]()
Solution:
Solve ![]() .
.
To solve ![]() , as before, we solve
, as before, we solve ![]() .
.
Setting ![]() , we find only one zero of
, we find only one zero of ![]() :
: ![]() .
.
This one ![]() value divides the number line into two intervals, from which we choose
value divides the number line into two intervals, from which we choose ![]() and
and ![]() as test values. We find
as test values. We find ![]() and
and ![]() .
.
Because we are looking for solutions to ![]() , we are looking for
, we are looking for ![]() values where
values where ![]() as well as where
as well as where ![]() . Looking at our sign diagram, there are no places where
. Looking at our sign diagram, there are no places where ![]() (there are no
(there are no ![]() ), so our solution is only
), so our solution is only ![]() (where
(where ![]() ). We write this as
). We write this as ![]() .
.
Graphically, we solve ![]() by graphing
by graphing ![]() and
and ![]() . We are looking for the
. We are looking for the ![]() values where the graph of
values where the graph of ![]() (in red) is below the graph of
(in red) is below the graph of ![]() (in blue), for
(in blue), for ![]() , and/or where the two graphs intersect (
, and/or where the two graphs intersect (![]() ). Notice that the line and the parabola touch at
). Notice that the line and the parabola touch at ![]() , but the parabola is always above the line otherwise.[7]
, but the parabola is always above the line otherwise.[7]

Example 4.4.1.4
Solve the following inequalities analytically[8] and check your solutions graphically.
![]()
Solution:
Solve ![]() .
.
To solve ![]() analytically we first rewrite the absolute value using cases.
analytically we first rewrite the absolute value using cases.
For ![]() ,
, ![]() , so we get
, so we get ![]() which simplifies to
which simplifies to ![]() .
.
Finding the zeros of ![]() , we get
, we get ![]() and
and ![]() .
.
However, we are concerned only with the portion of the number line where ![]() , so the only zero that we deal with is
, so the only zero that we deal with is ![]() . This divides the interval
. This divides the interval ![]() into two intervals:
into two intervals: ![]() and
and ![]() .
.
We choose ![]() and
and ![]() as our test values. We find
as our test values. We find ![]() and
and ![]() .
.
Hence, our solution to ![]() for
for ![]() is
is ![]() .
.
Next, we turn our attention to the case ![]() . Here,
. Here, ![]() , so our original inequality becomes
, so our original inequality becomes ![]() , or
, or ![]() .
.
Setting ![]() , we find the zeros of
, we find the zeros of ![]() to be
to be ![]() and
and ![]() .
.
Of these, only ![]() lies in the region
lies in the region ![]() , so we ignore
, so we ignore ![]() . Our test intervals are now
. Our test intervals are now ![]() and
and ![]() . We choose
. We choose ![]() and
and ![]() as our test values and find
as our test values and find ![]() and
and ![]() .
.
Hence, our solution to ![]() , in this region is
, in this region is ![]() .
.
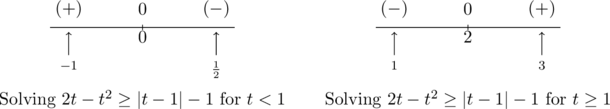
Combining these into one sign diagram, we have that our solution is ![]() .
.
Graphically, to check ![]() , we set
, we set ![]() (in red) and
(in red) and ![]() (in blue) and look for the
(in blue) and look for the ![]() values where the graph of
values where the graph of ![]() intersects or is above the the graph of
intersects or is above the the graph of ![]() . The combined sign chart is given on the left and the graphs are on the right.
. The combined sign chart is given on the left and the graphs are on the right.

We continue this section with an example that combines quadratic inequalities with piecewise functions.
Example 4.4.2
Example 4.4.2
Rewrite ![]() as a piecewise function and graph.
as a piecewise function and graph.
Solution:
Using the definition of absolute value, Definition 1.12 and the sign diagram we constructed for ![]() near the beginning of the subsection, we get:
near the beginning of the subsection, we get:
![Rendered by QuickLaTeX.com \[ \begin{array}{ccc} g(x) = |x^2-x-6| & = & \left\{ \begin{array}{cc} -(x^2-x-6) & \text{if } (x^2-x-6) < 0 \\ (x^2-x-6) & \text{if } (x^2-x-6) \geq 0 \\ \end{array} \right. \\[8pt] & = & \left\{ \begin{array}{cc} -x^2+x+6 & \text{if } -2 < x < 3 \\ x^2-x-6 & \text{if } x \leq -2 \text{ or } x \geq 3 \\ \end{array} \right. \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-bba825c2d992a901c820676fb10f7a55_l3.png)
Going through the usual machinations results on the graph on the right. Compare it to the graph on the left. Notice anything?
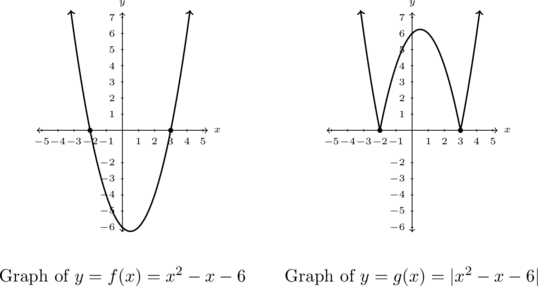
If we take a step back and look at the graphs of ![]() and
and ![]() , we notice that to obtain the graph of
, we notice that to obtain the graph of ![]() from the graph of
from the graph of ![]() , we reflect a portion of the graph of
, we reflect a portion of the graph of ![]() about the
about the ![]() -axis. In general, if
-axis. In general, if ![]() , then:
, then:
![]()
The function ![]() is defined so that when
is defined so that when ![]() is negative (i.e., when its graph is below the
is negative (i.e., when its graph is below the ![]() -axis), the graph of
-axis), the graph of ![]() is the reflection of the graph of
is the reflection of the graph of ![]() across the
across the ![]() -axis. This is a general method to graph functions of the form
-axis. This is a general method to graph functions of the form ![]() . Indeed, the graph of
. Indeed, the graph of ![]() can be obtained by reflection the portion of the line
can be obtained by reflection the portion of the line ![]() which is below the
which is below the ![]() -axis back above the
-axis back above the ![]() -axis creating the characteristic `
-axis creating the characteristic `![]() ‘ shape.[9]
‘ shape.[9]
4.4.2 Inequalities Involving Rational Functions and Applications
In this subsection, we solve equations and inequalities involving rational functions and explore associated application problems. Our first example showcases the critical difference in procedure between solving equations and inequalities.
Example 4.4.3
Example 4.4.3.1
Solve ![]() .
.
Solution:
Solve ![]() .
.
To solve the equation, we clear denominators
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{x^3-2x+1}{x-1} & = & \dfrac{1}{2}x-1 & \\ [10pt] \left(\dfrac{x^3-2x+1}{x-1}\right) \cdot 2(x-1) & = & \left( \dfrac{1}{2}x-1 \right) \cdot 2(x-1) & \\ [10pt] 2x^3 - 4x + 2 & = & x^2-3x+2 & \text{expand} \\ 2x^3 -x^2 - x & = & 0 & \\ x(2x+1)(x-1) & = & 0 & \text{factor}\\ x & = & -\frac{1}{2}, \, 0, \, 1 & \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-176ec96e16010eea8998b44bca4c594f_l3.png)
Due to the fact that we cleared denominators, we need to check for extraneous solutions. Sure enough, we see that ![]() does not satisfy the original equation, so our only solutions are
does not satisfy the original equation, so our only solutions are ![]() and
and ![]() .
.
Example 4.4.3.2
Solve ![]() .
.
Solution:
Solve ![]() .
.
To solve the inequality, it may be tempting to begin as we did with the equation ![]() namely by multiplying both sides by the quantity
namely by multiplying both sides by the quantity ![]() . The problem is that, depending on
. The problem is that, depending on ![]() ,
, ![]() may be positive (which doesn’t affect the inequality) or
may be positive (which doesn’t affect the inequality) or ![]() could be negative (which would reverse the inequality). Instead of working by cases, we collect all of the terms on one side of the inequality with 0 on the other and make a sign diagram using the technique given in Section 3.3.
could be negative (which would reverse the inequality). Instead of working by cases, we collect all of the terms on one side of the inequality with 0 on the other and make a sign diagram using the technique given in Section 3.3.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{x^3-2x+1}{x-1} & \geq & \dfrac{1}{2}x-1 & \\ [10pt] \dfrac{x^3-2x+1}{x-1} - \dfrac{1}{2} x + 1& \geq & 0& \\ [10pt] \dfrac{2 \left(x^3-2x+1\right)}{2(x-1)} - \dfrac{x(x-1)}{2(x-1)} + \dfrac{2(x-1)}{2(x-1)}& \geq & 0&\text{get a common denominator} \\ [10pt] \dfrac{2\left(x^3-2x+1\right)-x(x-1)+2(x-1)}{2(x-1)} & \geq & 0 & \\ [10pt] \dfrac{2x^3-x^2-x}{2x-2} & \geq & 0 & \text{expand} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-50e87024ca71e8db821baca40054d423_l3.png)
Viewing the left hand side as a rational function ![]() we make a sign diagram.
we make a sign diagram.
The only value excluded from the domain of ![]() is
is ![]() which is the solution to
which is the solution to ![]() . The zeros of
. The zeros of ![]() are the solutions to
are the solutions to ![]() , which we have already found to be
, which we have already found to be ![]() ,
, ![]() and
and ![]() , the latter was discounted as a zero because it is not in the domain.
, the latter was discounted as a zero because it is not in the domain.
Choosing test values in each test interval, we construct the sign diagram below.
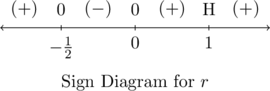
We are interested in where ![]() . We see
. We see ![]() , or
, or ![]() , on the intervals
, on the intervals ![]() ,
, ![]() and
and ![]() . We know
. We know ![]() when
when ![]() and
and ![]() .
.
Hence, ![]() on
on ![]() .
.
Example 4.4.3.3
Verify your solutions to 1 and 2 using a graph.
Solution:
To check our answers graphically, let ![]() and
and ![]() .
.
The solutions to ![]() are the
are the ![]() -coordinates of the points where the graphs of
-coordinates of the points where the graphs of ![]() and
and ![]() intersect. We graph both
intersect. We graph both ![]() (red) and
(red) and ![]() (blue) below.
(blue) below.
We find only two intersection points, ![]() and
and ![]() which correspond to our solutions
which correspond to our solutions ![]() and
and ![]() .
.
The solution to ![]() represents not only where the graphs meet, but the intervals over which the graph of
represents not only where the graphs meet, but the intervals over which the graph of ![]() is above (
is above (![]() ) the graph of
) the graph of ![]() . From the graph, this appears to happen on
. From the graph, this appears to happen on ![]() which almost matches the answer we found analytically.
which almost matches the answer we found analytically.
We have to remember that ![]() is not defined at
is not defined at ![]() , so it cannot be included in our solution.[10]
, so it cannot be included in our solution.[10]

The important take-away from Example 4.4.3 is not to clear fractions when working with an inequality unless you know for certain the sign of the denominators. We offer another example.
Example 4.4.4
Example 4.4.4
Solve: ![]() . Check your answer using a graph.
. Check your answer using a graph.
Solution:
We begin by rewriting the terms with negative exponents as fractions and gathering all nonzero terms to one side of the inequality:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 2t (3t-2)^{-1} & \leq & 3t^2 (3t-2)^{-2}& \\ [6pt] \dfrac{2t}{3t-2} & \leq & \dfrac{3t^2}{(3t-2)^2} & \\ [10pt] \dfrac{2t}{3t-2} - \dfrac{3t^2}{(3t-2)^2} & \leq & 0 & \\ [10pt] \dfrac{2t(3t-2)}{(3t-2)^2} - \dfrac{3t^2}{(3t-2)^2} & \leq & 0 & \text{get a common denominator} \\ [10pt] \dfrac{2t(3t-2) - 3t^2}{(3t-2)^2} & \leq & 0 &\\ [10pt] \dfrac{3t^2-4t}{(3t-2)^2} & \leq & 0 & \text{expand} \\ [10pt] \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-726a7e03ec6fedcd6a076d6855de6d14_l3.png)
We define ![]() and set about constructing a sign diagram for
and set about constructing a sign diagram for ![]() .
.
Solving ![]() gives
gives ![]() as our sole excluded value. To find the zeros of
as our sole excluded value. To find the zeros of ![]() , we set
, we set ![]() and solve
and solve ![]() . Factoring gives
. Factoring gives ![]() so our solutions are
so our solutions are ![]() and
and ![]() .
.
After choosing test values, we get the sign diagram below on the left. We are looking for where ![]() , we are looking for where
, we are looking for where ![]() is
is ![]() or
or ![]() .
.
Hence, our final answer is ![]() .
.
Below on the right, we graph ![]() and
and ![]() . Sure enough, the graph of
. Sure enough, the graph of ![]() intersects the graph of
intersects the graph of ![]() when
when ![]() and
and ![]() . Moreover, the graph of
. Moreover, the graph of ![]() is below the graph of
is below the graph of ![]() everywhere they are defined between these values, in accordance with our algebraic solution.
everywhere they are defined between these values, in accordance with our algebraic solution.

One thing to note about Example 4.4.4 is that the quantity ![]() for all values of
for all values of ![]() . Hence, as long as we remember
. Hence, as long as we remember ![]() is excluded from consideration, we could actually multiply both sides of the inequality in Example 4.4.4 by
is excluded from consideration, we could actually multiply both sides of the inequality in Example 4.4.4 by ![]() to obtain
to obtain ![]() . We could then solve this (slightly easier) inequality using the methods of Section 2.1 as long as we remember to exclude
. We could then solve this (slightly easier) inequality using the methods of Section 2.1 as long as we remember to exclude ![]() from our solution. Once again, the more you understand, the less you have to memorize. If you know the `why‘ behind an algorithm instead of just the `how,’ you will know when you can short-cut it.
from our solution. Once again, the more you understand, the less you have to memorize. If you know the `why‘ behind an algorithm instead of just the `how,’ you will know when you can short-cut it.
Our next example is an application of average cost. Recall from Definition 3.7 if ![]() represents the cost to make
represents the cost to make ![]() items then the average cost per item is given by
items then the average cost per item is given by ![]() , for
, for ![]() .
.
Example 4.4.5
Example 4.4.5.1
Recall from Example 1.3.8 that the cost, ![]() , in dollars, to produce
, in dollars, to produce ![]() PortaBoy game systems for a local retailer is
PortaBoy game systems for a local retailer is ![]() ,
, ![]() .
.
Write an expression for the average cost function, ![]() .
.
Solution:
Write an expression for the average cost function, ![]() .
.
From ![]() , we obtain
, we obtain ![]() .
.
The domain of ![]() is
is ![]() , but remember
, but remember ![]() causes problems for
causes problems for ![]() , so we get our domain to be
, so we get our domain to be ![]() , or
, or ![]() .
.
Example 4.4.5.2
Recall from Example 1.3.8 that the cost, ![]() , in dollars, to produce
, in dollars, to produce ![]() PortaBoy game systems for a local retailer is
PortaBoy game systems for a local retailer is ![]() ,
, ![]() .
.
Solve ![]() and interpret.
and interpret.
Solution:
Solve ![]() and interpret.
and interpret.
Solving ![]() means we solve
means we solve ![]() . We proceed as in the previous example.
. We proceed as in the previous example.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{80x+150}{x} & < & 100 & \\ [10pt] \dfrac{80x+150}{x} - 100 & < & 0 & \\ [10pt] \dfrac{80x + 150 - 100x}{x} & < & 0 & \text{common denominator} \\ [10pt] \dfrac{150 - 20x}{x} & < & 0 & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a4daa75199f96ff976aad038134ef1ad_l3.png)
If we take the left hand side to be a rational function ![]() , we need to keep in mind that the applied domain of the problem is
, we need to keep in mind that the applied domain of the problem is ![]() . This means we consider only the positive half of the number line for our sign diagram. On
. This means we consider only the positive half of the number line for our sign diagram. On ![]() ,
, ![]() is defined everywhere so we need only look for zeros of
is defined everywhere so we need only look for zeros of ![]() . Setting
. Setting ![]() gives
gives ![]() , so that
, so that ![]() . The test intervals on our domain are
. The test intervals on our domain are ![]() and
and ![]() . We find
. We find ![]() on
on ![]() .
.

In the context of the problem, ![]() represents the number of PortaBoy games systems produced and
represents the number of PortaBoy games systems produced and ![]() is the average cost to produce each system. Solving
is the average cost to produce each system. Solving ![]() means we are trying to find how many systems we need to produce so that the average cost is less than 100 dollars per system. Our solution,
means we are trying to find how many systems we need to produce so that the average cost is less than 100 dollars per system. Our solution, ![]() tells us that we need to produce more than
tells us that we need to produce more than ![]() systems to achieve this. Because it doesn’t make sense to produce half a system, our final answer is
systems to achieve this. Because it doesn’t make sense to produce half a system, our final answer is ![]() .
.
Example 4.4.5.3
Recall from Example 1.3.8 that the cost, ![]() , in dollars, to produce
, in dollars, to produce ![]() PortaBoy game systems for a local retailer is
PortaBoy game systems for a local retailer is ![]() ,
, ![]() .
.
Determine the behavior of ![]() as
as ![]() and interpret.
and interpret.
Solution:
Determine the behavior of ![]() as
as ![]() and interpret.
and interpret.
When we apply Theorem 3.3 to ![]() we find that
we find that ![]() is a horizontal asymptote to the graph of
is a horizontal asymptote to the graph of ![]() . To more precisely determine the behavior of
. To more precisely determine the behavior of ![]() as
as ![]() , we first use long division[11] and rewrite
, we first use long division[11] and rewrite ![]()
As ![]() ,
, ![]() , which means
, which means
![]()
Thus the average cost per system is getting closer to 80 dollars per system.
If we set ![]() , we get
, we get ![]() , which is impossible, so we conclude that
, which is impossible, so we conclude that ![]() for all
for all ![]() . This means that the average cost per system is always greater than 80 dollars per system, but the average cost is approaching this amount as more and more systems are produced. Looking back at Example 1.3.8 we realize 80 dollars is the variable cost per system
. This means that the average cost per system is always greater than 80 dollars per system, but the average cost is approaching this amount as more and more systems are produced. Looking back at Example 1.3.8 we realize 80 dollars is the variable cost per system ![]() the cost per system above and beyond the fixed initial cost of 150 dollars. Another way to interpret our answer is that `infinitely’ many systems would need to be produced to effectively `zero out’ the fixed cost.
the cost per system above and beyond the fixed initial cost of 150 dollars. Another way to interpret our answer is that `infinitely’ many systems would need to be produced to effectively `zero out’ the fixed cost.
Note that number 2 in Example 4.4.5 is another opportunity to short-cut the standard algorithm and obtain the solution more quickly if we take stock of the situation. The applied domain is ![]() , so we can multiply through the inequality
, so we can multiply through the inequality ![]() by
by ![]() without worrying about changing the sense of the inequality. This reduces the problem to
without worrying about changing the sense of the inequality. This reduces the problem to ![]() , a basic linear inequality whose solution is readily seen to be
, a basic linear inequality whose solution is readily seen to be ![]() . It is absolutely critical here that
. It is absolutely critical here that ![]() . Indeed, any time you decide to multiply an inequality by a variable expression, it is necessary to justify why the inequality is preserved. Our next example is another classic `box with no top’ problem. The reader is encouraged to compare and contrast this problem with Example 2.2.4 in Section 2.2.
. Indeed, any time you decide to multiply an inequality by a variable expression, it is necessary to justify why the inequality is preserved. Our next example is another classic `box with no top’ problem. The reader is encouraged to compare and contrast this problem with Example 2.2.4 in Section 2.2.
Example 4.4.6
Example 4.4.6.1
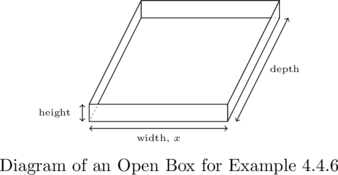
A box with a square base and no top is to be constructed so that it has a volume of ![]() cubic centimeters. Let
cubic centimeters. Let ![]() denote the width of the box, in centimeters as seen below.
denote the width of the box, in centimeters as seen below.
Explain why the height of the box (in centimeters) is a function of the width ![]() . Call this function
. Call this function ![]() and write an expression for
and write an expression for ![]() , complete with an appropriate applied domain.
, complete with an appropriate applied domain.
Solution:
Explain why the height of the box (in centimeters) is a function of the width ![]() . Call this function
. Call this function ![]() and write an expression for
and write an expression for ![]() , complete with an appropriate applied domain.
, complete with an appropriate applied domain.
We are told that the volume of the box is ![]() cubic centimeters and that
cubic centimeters and that ![]() represents the width, in centimeters. As
represents the width, in centimeters. As ![]() represents a physical dimension of a box, we have that
represents a physical dimension of a box, we have that ![]() . From geometry, we know
. From geometry, we know ![]() \times
\times![]() \times
\times![]() .
.
The base of the box is a square, so the width and the depth are both ![]() centimeters. Hence,
centimeters. Hence, ![]() . Solving for the height, we get
. Solving for the height, we get ![]() .
.
In other words, for each width ![]() , we are able to compute the[12] corresponding height using the formula
, we are able to compute the[12] corresponding height using the formula ![]() . Hence, the height is a function of
. Hence, the height is a function of ![]() .
.
Using function notation, we write ![]() . As mentioned before, our only restriction is
. As mentioned before, our only restriction is ![]() so the domain of
so the domain of ![]() is
is ![]() .
.
Example 4.4.6.2
A box with a square base and no top is to be constructed so that it has a volume of ![]() cubic centimeters. Let
cubic centimeters. Let ![]() denote the width of the box, in centimeters as seen below.
denote the width of the box, in centimeters as seen below.

Solve ![]() and interpret.
and interpret.
Solution:
Solve ![]() and interpret.
and interpret.
To solve ![]() , we proceed as before and collect all nonzero terms on one side of the inequality in order to use a sign diagram.
, we proceed as before and collect all nonzero terms on one side of the inequality in order to use a sign diagram.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} h(x) & \geq & x & \\ [10pt] \dfrac{1000}{x^2} & \geq & x & \\ [10pt] \dfrac{1000}{x^2} - x & \geq & 0 \\ [10pt] \dfrac{1000-x^3}{x^2} & \geq & 0 & \text{common denominator} \\[10pt] \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-bf5614b00ffc4ee956417dc18576c9e8_l3.png)
We consider the left hand side of the inequality as our rational function ![]() . We see immediately the only value excluded from the domain of
. We see immediately the only value excluded from the domain of ![]() is
is ![]() , but our applied domain is
, but our applied domain is ![]() , thus we restrict our attention to the interval
, thus we restrict our attention to the interval ![]() . The sole zero of
. The sole zero of ![]() comes when
comes when ![]() , or when
, or when ![]() .
.
Choosing test values in the intervals ![]() and
and ![]() gives the following:
gives the following:

We see ![]() on
on ![]() , and because
, and because ![]() at
at ![]() , our solution is
, our solution is ![]() .
.
In the context of the problem, ![]() represents the height of the box while
represents the height of the box while ![]() represents the width (and depth) of the box. Solving
represents the width (and depth) of the box. Solving ![]() is tantamount to finding the values of
is tantamount to finding the values of ![]() which result in a box where the height is at least as big as the width (and, in this case, depth.) Our answer tells us the width of the box can be at most
which result in a box where the height is at least as big as the width (and, in this case, depth.) Our answer tells us the width of the box can be at most ![]() centimeters for this to happen.[13]
centimeters for this to happen.[13]
Example 4.4.6.3
A box with a square base and no top is to be constructed so that it has a volume of ![]() cubic centimeters. Let
cubic centimeters. Let ![]() denote the width of the box, in centimeters as seen below.
denote the width of the box, in centimeters as seen below.

Determine and interpret the behavior of ![]() as
as ![]() and as
and as ![]() .
.
Solution:
Determine and interpret the behavior of ![]() as
as ![]() and as
and as ![]() .
.
As ![]() ,
, ![]() .
.
This means that the smaller the width ![]() (and, in this case, depth), the larger the height
(and, in this case, depth), the larger the height ![]() has to be in order to maintain a volume of 1000 cubic centimeters.
has to be in order to maintain a volume of 1000 cubic centimeters.
As ![]() , we find
, we find ![]() , which means that in order to maintain a volume of 1000 cubic centimeters, the width and depth must get bigger as the height becomes smaller.
, which means that in order to maintain a volume of 1000 cubic centimeters, the width and depth must get bigger as the height becomes smaller.
Example 4.4.6.4
A box with a square base and no top is to be constructed so that it has a volume of ![]() cubic centimeters. Let
cubic centimeters. Let ![]() denote the width of the box, in centimeters as seen below.
denote the width of the box, in centimeters as seen below.

Express the surface area of the box as a function of ![]() ,
, ![]() and state the applied domain.
and state the applied domain.
Solution:
Express the surface area of the box as a function of ![]() ,
, ![]() and state the applied domain.
and state the applied domain.
As a result of the box having no top, the surface area can be found by adding the area of each of the sides to the area of the base. The base is a square of dimensions ![]() by
by ![]() , and each side has dimensions
, and each side has dimensions ![]() by
by ![]() . We get the surface area,
. We get the surface area,
![]()
But ![]() , so we have
, so we have
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} S(x) & = & x^2+4x \left( \frac{1000}{x^2}\right) \\[6pt] & = & x^2 + \frac{4000}{x} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c4bf0b9ca661ceda504ef17f8bd354a7_l3.png)
The domain of ![]() is the same as
is the same as ![]() , namely
, namely ![]() , for the same reasons as above.
, for the same reasons as above.
Example 4.4.6.5
A box with a square base and no top is to be constructed so that it has a volume of ![]() cubic centimeters. Let
cubic centimeters. Let ![]() denote the width of the box, in centimeters as seen below.
denote the width of the box, in centimeters as seen below.

Use technology to approximate (to two decimal places) the dimensions of the box which minimize the surface area.
Solution:
Use technology to approximate (to two decimal places) the dimensions of the box which minimize the surface area.
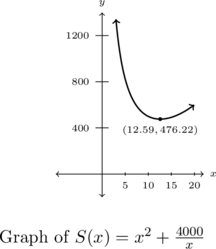
To graph ![]() , we create a table of values. Doing so, we find a local minimum when
, we create a table of values. Doing so, we find a local minimum when ![]() . As far as we can tell,[14] this is the only local extremum, so it is the (absolute) minimum as well. This means that the width and depth of the box should each measure approximately 12.60 centimeters. To determine the height, we find
. As far as we can tell,[14] this is the only local extremum, so it is the (absolute) minimum as well. This means that the width and depth of the box should each measure approximately 12.60 centimeters. To determine the height, we find ![]() , so the height of the box should be approximately
, so the height of the box should be approximately ![]() centimeters.[15]
centimeters.[15]
4.4.3 Inequalities Involving Power and Root Functions
Next, we move on to solving inequalities with power functions. As we’ve seen with other types of non-linear inequalities,[16] an invaluable tool for us is the Sign Diagram.
Steps for Constructing a Sign Diagram for an Algebraic Function
Suppose ![]() is an algebraic function.
is an algebraic function.
- Place any values excluded from the domain of
 on the number line with a dashed above them.
on the number line with a dashed above them. - Find the zeros of
 and place them on the number line with the number 0 above them.
and place them on the number line with the number 0 above them. - Choose a test value in each of the intervals determined in steps 1 and 2.
- Determine and record the sign of
 for each test value in step 3.
for each test value in step 3.
As you may recall, sign diagrams compare functions to 0, thus the first step in solving inequalities using a sign diagram is to gather all the nonzero terms one one side of the inequality. We demonstrate this technique in the following example.
Example 4.4.7
Example 4.4.7.1
Solve the following inequalities. Check your answers graphically.
![]()
Solution:
Solve ![]() .
.
To solve ![]() , it is tempting to rewrite this inequality as
, it is tempting to rewrite this inequality as ![]() and rid ourselves of the fourth root by raising both sides of this inequality to the fourth power. While this technique works sometimes, it doesn’t work all the time because raising both sides of an inequality to the fourth (more generally, to an even) power does not necessarily preserve inequalities.[17] For that reason, we solve this inequality using a sign diagram as this technique will always produce a correct solution.
and rid ourselves of the fourth root by raising both sides of this inequality to the fourth power. While this technique works sometimes, it doesn’t work all the time because raising both sides of an inequality to the fourth (more generally, to an even) power does not necessarily preserve inequalities.[17] For that reason, we solve this inequality using a sign diagram as this technique will always produce a correct solution.
We already have all the nonzero terms on one side of the inequality, so we let ![]() and proceed to make a sign diagram. Owing to the presence of the fourth root, we know
and proceed to make a sign diagram. Owing to the presence of the fourth root, we know ![]() or
or ![]() . Hence, we only concern ourselves with the portion of the number line representing
. Hence, we only concern ourselves with the portion of the number line representing ![]() .
.
Next, we find the zeros of ![]() by solving
by solving ![]() . We get
. We get ![]() , so
, so ![]() and we get
and we get ![]() . We find this solution checks in our original equation,[18] and proceed to construct the sign diagram below on the left. As we are looking for where
. We find this solution checks in our original equation,[18] and proceed to construct the sign diagram below on the left. As we are looking for where ![]() , we are looking for the zeros of
, we are looking for the zeros of ![]() along with the intervals over which
along with the intervals over which ![]() is
is ![]() .
.
We record our answer as ![]() .
.
Below is the graph of ![]() , and we can see that, indeed, the graph is above the
, and we can see that, indeed, the graph is above the ![]() -axis (
-axis (![]() ) from
) from ![]() and meets the
and meets the ![]() -axis at
-axis at ![]() , verifying our answer.
, verifying our answer.

Example 4.4.7.2
Solve the following inequalities. Check your answers graphically.
![]()
Solution:
Solve ![]() .
.
To solve ![]() , we first rewrite as
, we first rewrite as ![]() .
.
We set ![]() and note that the denominators in the exponents are
and note that the denominators in the exponents are ![]() , so they correspond to cube roots, which means the domain of
, so they correspond to cube roots, which means the domain of ![]() is
is ![]() .
.
To find the zeros for the sign diagram, we set ![]() and attempt to solve
and attempt to solve ![]() .
.
As a result of there being three terms, and the exponent on one of the variable terms, ![]() , is exactly twice that of the other,
, is exactly twice that of the other, ![]() , we have ourselves a `quadratic in disguise.’ If we let
, we have ourselves a `quadratic in disguise.’ If we let ![]() , then
, then ![]() , so in terms of
, so in terms of ![]() , we have
, we have ![]() .
.
Solving we get ![]() or
or ![]() , hence
, hence ![]() or
or ![]() .
.
In root-power notation, these are ![]() or
or ![]() . Cubing both sides of these equations results in
. Cubing both sides of these equations results in ![]() , which admits no real solution, or
, which admits no real solution, or ![]() , which gives
, which gives ![]() .
.
Using these zeros, we construct the sign diagram below on the left.
We find ![]() on
on ![]() .
.
To check our answer graphically, we set ![]() and
and ![]() . The solution to
. The solution to ![]() corresponds to the inequality
corresponds to the inequality ![]() , which means we are looking for the
, which means we are looking for the ![]() values for which the graph of
values for which the graph of ![]() is below the graph of
is below the graph of ![]() . On the graph below, we see the graph of
. On the graph below, we see the graph of ![]() is below the graph of
is below the graph of ![]() for
for ![]() and again for
and again for ![]() , which are the grapher’s approximations to
, which are the grapher’s approximations to ![]() .
.

Example 4.4.7.3
Solve the following inequalities. Check your answers graphically.
![]()
Solution:
Solve ![]() .
.
To solve ![]() , we first gather all the nonzero terms to one side and obtain
, we first gather all the nonzero terms to one side and obtain ![]() . Setting
. Setting ![]() , because the denominators of the rational exponents are odd, we have no domain concerns owing to even indexed roots. However, the negative exponent on the second term indicates a denominator. Rewriting
, because the denominators of the rational exponents are odd, we have no domain concerns owing to even indexed roots. However, the negative exponent on the second term indicates a denominator. Rewriting ![]() with positive exponents, we obtain
with positive exponents, we obtain
![]()
Setting the denominator equal to zero we get ![]() , which reduces to
, which reduces to ![]() , or
, or ![]() . Hence, the domain of
. Hence, the domain of ![]() is
is ![]() .
.
To find the zeros of ![]() , we set
, we set ![]() , so we set about solving
, so we set about solving
![]()
Clearing denominators, we get ![]() . As the denominators of the exponents are odd, we may use Theorem 4.3 to simplify this to
. As the denominators of the exponents are odd, we may use Theorem 4.3 to simplify this to ![]() , and obtain
, and obtain ![]() or
or ![]() . In order for us to be able to more easily determine the sign of
. In order for us to be able to more easily determine the sign of ![]() at the test values, we rewrite
at the test values, we rewrite ![]() as a single term.[19] There are two schools of thought on how to proceed, so we demonstrate both.
as a single term.[19] There are two schools of thought on how to proceed, so we demonstrate both.
- Factoring Approach: From
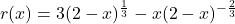 , we note that the quantity
, we note that the quantity  is common to both terms. When we factor out common factors, we factor out the quantity with the smaller exponent. In this case, we note
is common to both terms. When we factor out common factors, we factor out the quantity with the smaller exponent. In this case, we note 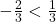 , so we factor
, so we factor 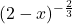 from both quantities. While it may seem odd to do so, we need to factor
from both quantities. While it may seem odd to do so, we need to factor 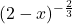 from
from 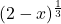 , which results in subtracting the exponent
, which results in subtracting the exponent 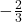 from
from 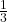 . We proceed using the usual properties of exponents.
. We proceed using the usual properties of exponents.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} r(x) & = & 3 (2-x)^{\frac{1}{3}} - x (2-x)^{-\frac{2}{3}} & \\ [3pt] & = & (2-x)^{-\frac{2}{3}} \left[ 3 (2-x)^{\frac{1}{3} - \left(-\frac{2}{3}\right)} - x\right] & \\ [6pt] & = & (2-x)^{-\frac{2}{3}}\left[3(2-x)^{\frac{3}{3}} - x\right] & \\ [3pt] & = & (2-x)^{-\frac{2}{3}}\left[3(2-x)^{1} - x\right] & \\ [3pt] & = & (2-x)^{-\frac{2}{3}}\left(6-4x\right) & \\ [3pt] & = & (2-x)^{-\frac{2}{3}}\left(6-4x\right) & \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-fd99d2827ade233ef7ac040f394bbd4a_l3.png)
Written without negative exponents, we have
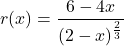 .
. - Common Denominator Approach: We rewrite
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} r(x) & = & 3 (2-x)^{\frac{1}{3}} - x (2-x)^{-\frac{2}{3}} & \\ [3pt] & = & 3 (2-x)^{\frac{1}{3}} - \dfrac{x}{(2-x)^{\frac{2}{3}}} & \\ [10pt] & = & \dfrac{3 (2-x)^{\frac{1}{3}}(2-x)^{\frac{2}{3}}}{(2-x)^{\frac{2}{3}}} - \dfrac{x}{(2-x)^{\frac{2}{3}}} & \text{common denominator} \\ [10pt] & = & \dfrac{3 (2-x)^{\frac{1}{3} + \frac{2}{3}}}{(2-x)^{\frac{2}{3}}} - \dfrac{x}{(2-x)^{\frac{2}{3}}} & \text{Theorem 4.3} \\ [10pt] & = & \dfrac{3 (2-x)^{\frac{3}{3}}}{(2-x)^{\frac{2}{3}}} - \dfrac{x}{(2-x)^{\frac{2}{3}}} & \\ [10pt] & = & \dfrac{3 (2-x)^1}{(2-x)^{\frac{2}{3}}} - \dfrac{x}{(2-x)^{\frac{2}{3}}} & \\ [10pt] & = & \dfrac{3 (2-x) - x}{(2-x)^{\frac{2}{3}}} & \\ [10pt] & = & \dfrac{6-4x}{(2-x)^{\frac{2}{3}}} & \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-1a3cbe661c3bfc69162032557bcfb2a0_l3.png)
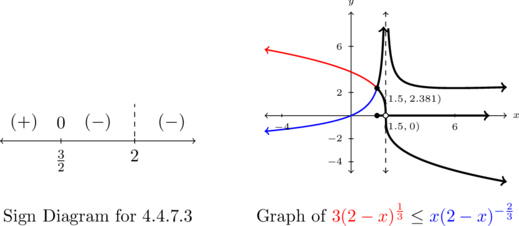
Using either approach, we end up with the same, simpler, expression for ![]() and we use that to create our sign diagram as shown below on the left. We find
and we use that to create our sign diagram as shown below on the left. We find ![]() on
on ![]() .
.
To check this graphically, we set ![]() and
and ![]() . We confirm that the graphs intersect at
. We confirm that the graphs intersect at ![]() and the graph of
and the graph of ![]() is below the graph of
is below the graph of ![]() for
for ![]() , with the exception of
, with the exception of ![]() where it appears the graph of
where it appears the graph of ![]() has a vertical asymptote.
has a vertical asymptote.
Example 4.4.7.4
Solve the following inequalities. Check your answers graphically.
![]()
Solution:
Solve ![]() .
.
While it may be tempting to begin solving our last inequality by clearing denominators, owing to the odd root, the quantity ![]() can be both positive and negative for different values of
can be both positive and negative for different values of ![]() . This means that if we chose to multiply both sides of our inequality by this quantity, we have no guarantee if the inequality would be preserved. Hence we proceed as usual by gathering all the nonzero terms to one side, and, with the ultimate goal of creating a sign diagram, get common denominators.
. This means that if we chose to multiply both sides of our inequality by this quantity, we have no guarantee if the inequality would be preserved. Hence we proceed as usual by gathering all the nonzero terms to one side, and, with the ultimate goal of creating a sign diagram, get common denominators.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} (t-4)^{\frac{2}{3}} & \geq & - \dfrac{2t}{3(t-4)^{\frac{1}{3}}} & \\ (t-4)^{\frac{2}{3}} + \dfrac{2t}{3(t-4)^{\frac{1}{3}}} & \geq & 0 \\ \dfrac{ (t-4)^{\frac{2}{3}} \cdot 3(t-4)^{\frac{1}{3}} }{3(t-4)^{\frac{1}{3}}} + \dfrac{2t}{3(t-4)^{\frac{1}{3}}} & \geq & 0 & \text{common denominator} \\ \dfrac{3(t-4)^{\frac{2}{3}+\frac{1}{3}}}{3(t-4)^{\frac{1}{3}}} + \dfrac{2t}{3(t-4)^{\frac{1}{3}}} & \geq & 0 & \text{Theorem 4.3} \\ \dfrac{3(t-4)^{1}}{3(t-4)^{\frac{1}{3}}} + \dfrac{2t}{3(t-4)^{\frac{1}{3}}} & \geq & 0 & \\ \dfrac{3(t-4) + 2t}{3(t-4)^{\frac{1}{3}}} & \geq & 0 & \\ \dfrac{5t-12}{3(t-4)^{\frac{1}{3}}} & \geq & 0 & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-eb9423ae9ba7dbfd0e47556a2e034d9b_l3.png)
We identify ![]() as the left hand side of the inequality and see right away we must exclude
as the left hand side of the inequality and see right away we must exclude ![]() from the domain owing to the quantity
from the domain owing to the quantity ![]() in the denominator.
in the denominator.
As we have already mentioned, the root here (![]() ) is odd, so we have no domain issues stemming from that. To find the zeros of
) is odd, so we have no domain issues stemming from that. To find the zeros of ![]() , we set
, we set ![]() which quickly reduces to solving
which quickly reduces to solving ![]() . We get
. We get ![]() .
.
From the sign diagram, we find ![]() on
on ![]() .
.
Graphing ![]() and
and ![]() , we see the graph of
, we see the graph of ![]() is above the graph of
is above the graph of ![]() for
for ![]() and again for
and again for ![]() , with an intersection point at
, with an intersection point at ![]() .
.

Note that in Example4.4.3 number 3, because ![]() is always positive for
is always positive for ![]() (owing to the squared exponent), we could have short-cut the sign diagram, choosing to clear denominators instead:
(owing to the squared exponent), we could have short-cut the sign diagram, choosing to clear denominators instead:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 3 (2-x)^{\frac{1}{3}} & \leq & x (2-x)^{-\frac{2}{3}} & \\ 3 (2-x)^{\frac{1}{3}} & \leq & \dfrac{x}{(2-x)^{\frac{2}{3}}} & \\ \left[3 (2-x)^{\frac{1}{3}} \right] \left[ (2-x)^{\frac{2}{3}}\right]& \leq & \dfrac{x}{(2-x)^{\frac{2}{3}}} \left[ (2-x)^{\frac{2}{3}}\right]& \text{provided } x \neq 2 \\ 3 (2-x)^{\frac{1}{3}} (2-x)^{\frac{2}{3}} & \leq & x& \\ 3 (2-x)^{\frac{1}{3}+\frac{2}{3}} & \leq & x& \\ 3(2-x) & \leq & x & \\ 6-3x & \leq & x &\\ x & \geq & \frac{3}{2} & \text{provided } x \neq 2 \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-8502cc19dc81bda0111d3a6fb9047425_l3.png)
This matches our solution ![]() . If, on the other hand, we tried this same manipulation with number 4, we would clear denominators, assuming
. If, on the other hand, we tried this same manipulation with number 4, we would clear denominators, assuming ![]() to obtain
to obtain ![]() or
or ![]() which is not the correct solution. The moral of the story is the more you understand, the less you need to rely on memorized processes and the more efficient your solution methodologies can become. The sign diagram algorithm is a fail-safe method, but, in some cases, may be far from the most efficient one. It’s always best to understand the why of a procedure as much as the how.
which is not the correct solution. The moral of the story is the more you understand, the less you need to rely on memorized processes and the more efficient your solution methodologies can become. The sign diagram algorithm is a fail-safe method, but, in some cases, may be far from the most efficient one. It’s always best to understand the why of a procedure as much as the how.
4.4.4 Section Exercises
In Exercises 1 – 16, solve the inequality. Write your answer using interval notation.
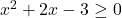
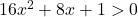
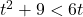
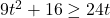
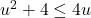
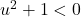
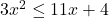
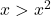
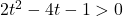
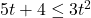
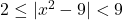
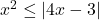
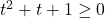
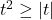
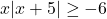
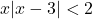
- The height of an object dropped from the roof of an eight story building is modeled by by the function
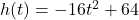 ,
, 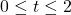 . Here,
. Here, 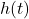 is the height of the object off the ground, in feet,
is the height of the object off the ground, in feet,  seconds after the object is dropped. How long before the object hits the ground?
seconds after the object is dropped. How long before the object hits the ground? - The height
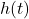 in feet of a model rocket above the ground
in feet of a model rocket above the ground  seconds after lift-off is given by the function
seconds after lift-off is given by the function 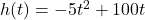 , for
, for 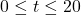 . When does the rocket reach its maximum height above the ground? What is its maximum height?
. When does the rocket reach its maximum height above the ground? What is its maximum height? - Carl’s friend Jason participates in the Highland Games. In one event, the hammer throw, the height
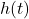 in feet of the hammer above the ground
in feet of the hammer above the ground  seconds after Jason lets it go is modeled by the function
seconds after Jason lets it go is modeled by the function 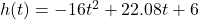 . What is the hammer’s maximum height? What is the hammer’s total time in the air? Round your answers to two decimal places.
. What is the hammer’s maximum height? What is the hammer’s total time in the air? Round your answers to two decimal places. - Assuming no air resistance or forces other than the Earth’s gravity, the height above the ground at time
 of a falling object is given by
of a falling object is given by 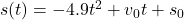 where
where  is in meters,
is in meters,  is in seconds,
is in seconds, 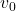 is the object’s initial velocity in meters per second and
is the object’s initial velocity in meters per second and 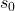 is its initial position in meters.
is its initial position in meters.
- What is the applied domain of this function?
- Discuss with your classmates what each of
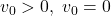 and
and  would mean.
would mean. - Come up with a scenario in which
 .
. - Let’s say a slingshot is used to shoot a marble straight up from the ground
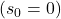 with an initial velocity of 15 meters per second. What is the marble’s maximum height above the ground? At what time will it hit the ground?
with an initial velocity of 15 meters per second. What is the marble’s maximum height above the ground? At what time will it hit the ground? - If the marble is shot from the top of a 25 meter tall tower, when does it hit the ground?
- What would the height function be if instead of shooting the marble up off of the tower, you were to shoot it straight DOWN from the top of the tower?
- Graph
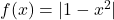
- Find all of the points on the line
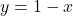 which are
which are 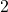 units from
units from 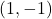 .
. - Let
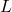 be the line
be the line 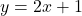 . Find a function
. Find a function 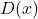 which measures the distance squared from a point on
which measures the distance squared from a point on 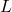 to
to 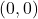 . Use this to find the point on
. Use this to find the point on 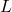 closest to
closest to 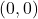 .
.
(Review of Solving Equations):[20] In Exercises 24 – 29, solve the rational equation. Be sure to check for extraneous solutions.
In Exercises 30 – 45, solve the rational inequality. Express your answer using interval notation.
In Exercises 46 – 51, use the the graph of the given rational function to solve the stated inequality.
- Solve
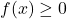 .
.
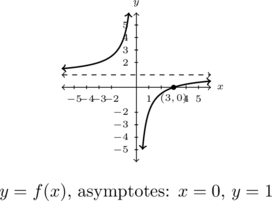
- Solve
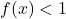 .
.

- Solve
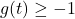 .
.
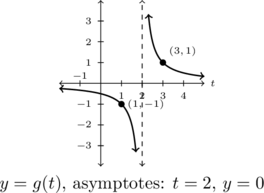
- Solve
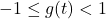 .
.

- Solve
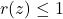

- Solve
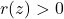 .
.
- In Exercise 55 in Section 2.2, the function
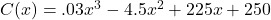 , for
, for 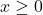 was used to model the cost (in dollars) to produce
was used to model the cost (in dollars) to produce  PortaBoy game systems. Using this cost function, find the number of PortaBoys which should be produced to minimize the average cost
PortaBoy game systems. Using this cost function, find the number of PortaBoys which should be produced to minimize the average cost  . Round your answer to the nearest number of systems.
. Round your answer to the nearest number of systems. - Suppose we are in the same situation as Example 4.4.6. If the volume of the box is to be
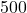 cubic centimeters, use a graphing utility to find the dimensions of the box which minimize the surface area. What is the minimum surface area? Round your answers to two decimal places.
cubic centimeters, use a graphing utility to find the dimensions of the box which minimize the surface area. What is the minimum surface area? Round your answers to two decimal places. - The box for the new Sasquatch-themed cereal, `Crypt-Os’, is to have a volume of
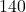 cubic inches. For aesthetic reasons, the height of the box needs to be
cubic inches. For aesthetic reasons, the height of the box needs to be 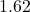 times the width of the base of the box.[21] Find the dimensions of the box which will minimize the surface area of the box. What is the minimum surface area? Round your answers to two decimal places.
times the width of the base of the box.[21] Find the dimensions of the box which will minimize the surface area of the box. What is the minimum surface area? Round your answers to two decimal places. - Sally is Skippy’s neighbor from Exercise 23 in Section 2.1. Sally also wants to plant a vegetable garden along the side of her home. She doesn’t have any fencing, but wants to keep the size of the garden to 100 square feet. What are the dimensions of the garden which will minimize the amount of fencing she needs to buy? What is the minimum amount of fencing she needs to buy? Round your answers to the nearest foot. (Note: Since one side of the garden will border the house, Sally doesn’t need fencing along that side.)
- Another Classic Problem: A can is made in the shape of a right circular cylinder and is to hold one pint. (For dry goods, one pint is equal to
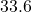 cubic inches.)[22]
cubic inches.)[22]
- Write an expression for the volume
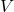 of the can in terms of the height
of the can in terms of the height  and the base radius
and the base radius  .
. - Write an expression for the surface area
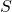 of the can in terms of the height
of the can in terms of the height  and the base radius
and the base radius  . (Hint: The top and bottom of the can are circles of radius
. (Hint: The top and bottom of the can are circles of radius  and the side of the can is really just a rectangle that has been bent into a cylinder.)
and the side of the can is really just a rectangle that has been bent into a cylinder.) - Using the fact that
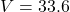 , write
, write 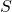 as a function of
as a function of  and state its applied domain.
and state its applied domain. - Use a graph to determine the dimensions of the can which has minimal surface area.
- Write an expression for the volume
- A right cylindrical drum is to hold 7.35 cubic feet of liquid. Find the dimensions (radius of the base and height) of the drum which would minimize the surface area. What is the minimum surface area? Round your answers to two decimal places.
- In Exercise 35 in Section 3.2, the population of Sasquatch in Portage County is modeled by
![Rendered by QuickLaTeX.com \[P(t) = \frac{150t}{t + 15}, \quad t \geq 0,\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-ece773db6efc45139713ca7501b6e3ea_l3.png)
where
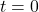 corresponds to the year 1803. According to this model, when were there fewer than 100 Sasquatch in Portage County?
corresponds to the year 1803. According to this model, when were there fewer than 100 Sasquatch in Portage County?
In Exercises 59 – 74, solve the inequalities and check your answer graphically.
- That is, if
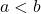 , then
, then 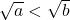 . ↵
. ↵ - Namely ones with a nonzero coefficient of `
 '. ↵
'. ↵ - By `solve analytically' we mean `algebraically' using a sign diagram. ↵
- We have to choose something in each interval. If you don't like our choices, please feel free to choose different numbers. You'll get the same sign chart. ↵
- By `solve analytically' we mean `algebraically' using a sign diagram. ↵
- By `solve analytically' we mean `algebraically' using a sign diagram. ↵
- In this case, we say the line
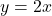 is tangent to
is tangent to 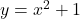 at
at 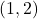 . Finding tangent lines to arbitrary functions is a fundamental problem solved, in general, with Calculus. ↵
. Finding tangent lines to arbitrary functions is a fundamental problem solved, in general, with Calculus. ↵ - By `solve analytically' we mean `algebraically' using a sign diagram. ↵
- See Exercise 11 in Section 1.4. ↵
- We invite the reader to show there is a hole in the graph of
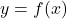 at
at 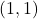 . ↵
. ↵ - In this case, long division amounts to term-by-term division. ↵
- that is, the one and only one ↵
- As with the previous example, knowing
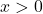 means
means 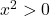 so we can clear denominators right away and solve
so we can clear denominators right away and solve 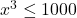 , or
, or 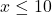 . Coupled with our applied domain,
. Coupled with our applied domain, 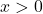 , we would arrive at the same solution,
, we would arrive at the same solution, ![Rendered by QuickLaTeX.com (0, 10]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d574aed930a8285f0c2cf2eee775e7cb_l3.png) . ↵
. ↵ - without Calculus, that is... ↵
- The
 -coordinate here, 476.22 means the minimum surface area possible is 476.22 square centimeters. Minimizing the surface area minimizes the material required to make the box, therein helping to reduce the cost of the box. ↵
-coordinate here, 476.22 means the minimum surface area possible is 476.22 square centimeters. Minimizing the surface area minimizes the material required to make the box, therein helping to reduce the cost of the box. ↵ - see subsections 4.4.1 and 4.4.2 ↵
- For instance,
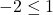 but
but 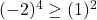 . We invite the reader to see what goes wrong if attempting to solve either of the following inequalities using this method:
. We invite the reader to see what goes wrong if attempting to solve either of the following inequalities using this method: ![Rendered by QuickLaTeX.com -2 \geq \sqrt[4]{x+3}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-6ba0822f5969318a520ee75e3a2035e7_l3.png) , which has no solution, or
, which has no solution, or ![Rendered by QuickLaTeX.com -2 \leq \sqrt[4]{x+3}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-fdfc9f7817363a86a8590443e61e87e4_l3.png) , whose solution is
, whose solution is 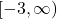 . ↵
. ↵ - Recall that raising both sides to an even power could produce extraneous solutions, so it is important we check here. ↵
- This also gives us a chance to review some good intermediate algebra! ↵
- For more review, see Section 3.1. ↵
- 1.62 is a crude approximation of the so-called `Golden Ratio'
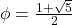 . ↵
. ↵ - According to www.dictionary.com, there are different values given for this conversion. We use
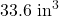 for this problem. ↵
for this problem. ↵

