5.1 Inverse Functions
In Section 1.2, we defined functions as processes. In this section, we seek to reverse, or `undo’ those processes. As in real life, we will find that some processes (like putting on socks and shoes) are reversible while some (like baking a cake) are not.
Consider the function ![]() . Starting with a real number input
. Starting with a real number input ![]() , we apply two steps in the following sequence: first we multiply the input by
, we apply two steps in the following sequence: first we multiply the input by ![]() and, second, we add
and, second, we add ![]() to the result.
to the result.
To reverse this process, we seek a function ![]() which will undo each of these steps and take the output from
which will undo each of these steps and take the output from ![]() ,
, ![]() , and return the input
, and return the input ![]() . If we think of the two-step process of first putting on socks then putting on shoes, to reverse the process, we first take off the shoes and then we take off the socks. In much the same way, the function
. If we think of the two-step process of first putting on socks then putting on shoes, to reverse the process, we first take off the shoes and then we take off the socks. In much the same way, the function ![]() should undo each step of
should undo each step of ![]() but in the opposite order. That is, the function
but in the opposite order. That is, the function ![]() should first subtract
should first subtract ![]() from the input
from the input ![]() then divide the result by
then divide the result by ![]() . This leads us to the formula
. This leads us to the formula ![]() .
.
Let’s check to see if the function ![]() does the job. If
does the job. If ![]() , then
, then ![]() . Taking the output 19 from
. Taking the output 19 from ![]() , we substitute it into
, we substitute it into ![]() to get
to get ![]() , which is our original input to
, which is our original input to ![]() . To check that
. To check that ![]() does the job for all
does the job for all ![]() in the domain of
in the domain of ![]() , we take the generic output from
, we take the generic output from ![]() ,
, ![]() , and substitute that into
, and substitute that into ![]() . That is, we simplify
. That is, we simplify ![]() , which is our original input to
, which is our original input to ![]() . If we carefully examine the arithmetic as we simplify
. If we carefully examine the arithmetic as we simplify ![]() , we actually see
, we actually see ![]() first `undoing’ the addition of
first `undoing’ the addition of ![]() , and then `undoing’ the multiplication by
, and then `undoing’ the multiplication by ![]() .
.
Not only does ![]() undo
undo ![]() , but
, but ![]() also undoes
also undoes ![]() . That is, if we take the output from
. That is, if we take the output from ![]() ,
, ![]() , and substitute that into
, and substitute that into ![]() , we get
, we get ![]() . Using the language of function composition developed in Section 1.5.2, the statements
. Using the language of function composition developed in Section 1.5.2, the statements ![]() and
and ![]() can be written as
can be written as ![]() and
and ![]() , respectively.[1] Abstractly, we can visualize the relationship between
, respectively.[1] Abstractly, we can visualize the relationship between ![]() and
and ![]() in the diagram below.
in the diagram below.
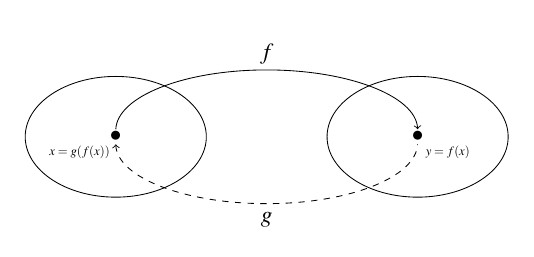
The main idea to get from the diagram is that ![]() takes the outputs from
takes the outputs from ![]() and returns them to their respective inputs, and conversely,
and returns them to their respective inputs, and conversely, ![]() takes outputs from
takes outputs from ![]() and returns them to their respective inputs. We now have enough background to state the central definition of the section.
and returns them to their respective inputs. We now have enough background to state the central definition of the section.
Definition 5.1
Suppose ![]() and
and ![]() are two functions such that
are two functions such that
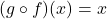 for all
for all  in the domain of
in the domain of  and
and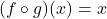 for all
for all  in the domain of
in the domain of 
then ![]() and
and ![]() are inverses of each other and the functions
are inverses of each other and the functions ![]() and
and ![]() are said to be invertible.
are said to be invertible.
If we abstract one step further, we can express the sentiment in Definition 5.1 by saying that ![]() and
and ![]() are inverses if and only if
are inverses if and only if ![]() and
and ![]() where
where ![]() is the identity function restricted[2] to the domain of
is the identity function restricted[2] to the domain of ![]() and
and ![]() is the identity function restricted to the domain of
is the identity function restricted to the domain of ![]() .
.
In other words, ![]() for all
for all ![]() in the domain of
in the domain of ![]() and
and ![]() for all
for all ![]() in the domain of
in the domain of ![]() . Using this description of inverses along with the properties of function composition listed in Theorem 1.6, we can show that function inverses are unique.[3]
. Using this description of inverses along with the properties of function composition listed in Theorem 1.6, we can show that function inverses are unique.[3]
Suppose ![]() and
and ![]() are both inverses of a function
are both inverses of a function ![]() . By Theorem 5.1, the domain of
. By Theorem 5.1, the domain of ![]() is equal to the domain of
is equal to the domain of ![]() , because both are the range of
, because both are the range of ![]() . This means the identity function
. This means the identity function ![]() applies both to the domain of
applies both to the domain of ![]() and the domain of
and the domain of ![]() Thus
Thus
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} h &=& h \circ I_{2} \\ &=& h \circ (f \circ g) \\ &=& (h \circ f) \circ g \\ &=& I_{1} \circ g \\ &=& g \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-6f3634e709ed18fc621d5df453ace689_l3.png)
as required.
We summarize the important properties of invertible functions in the following theorem. Apart from introducing notation, each of the results below are immediate consequences of the idea that inverse functions map the outputs from a function ![]() back to their corresponding inputs.
back to their corresponding inputs.
Theorem 5.1 Properties of Inverse Functions
Suppose ![]() is an invertible function.
is an invertible function.
- There is exactly one inverse function for
 , denoted
, denoted 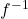 (read `
(read ` -inverse’)
-inverse’) - The range of
 is the domain of
is the domain of 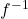 and the domain of
and the domain of  is the range of
is the range of 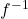
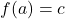 if and only if
if and only if 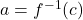
NOTE: In particular, for all in the range of
in the range of  , the solution to
, the solution to 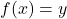 is
is 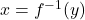
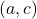 is on the graph of
is on the graph of  if and only if
if and only if 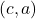 is on the graph of
is on the graph of 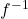
NOTE: This means graph of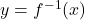 is the reflection of the graph of
is the reflection of the graph of 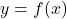 across
across 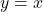 .[4]
.[4]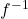 is an invertible function and
is an invertible function and 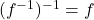
The notation ![]() is an unfortunate choice because you’ve been programmed since Algebra I to think of this as
is an unfortunate choice because you’ve been programmed since Algebra I to think of this as ![]() . This is most definitely not the case, for instance,
. This is most definitely not the case, for instance, ![]() has as its inverse
has as its inverse ![]() , which is certainly different than
, which is certainly different than ![]()
Why does this confusing notation persist? As we mentioned in Section 1.5.2, the identity function ![]() is to function composition what the real number
is to function composition what the real number ![]() is to real number multiplication. The choice of notation
is to real number multiplication. The choice of notation ![]() alludes to the property that
alludes to the property that ![]() and
and ![]() , in much the same way as
, in much the same way as ![]() and
and ![]() .
.
Before we embark on an example, we demonstrate the pertinent parts of Theorem 5.1 to the inverse pair ![]() and
and ![]() . Suppose we wanted to solve
. Suppose we wanted to solve ![]() . Going through the usual machinations, we obtain
. Going through the usual machinations, we obtain ![]() .
.
If we view this equation as ![]() , however, then we are looking for the input
, however, then we are looking for the input ![]() corresponding to the output
corresponding to the output ![]() . This is exactly the question
. This is exactly the question ![]() was built to answer. In other words, the solution to
was built to answer. In other words, the solution to ![]() is
is ![]() . In other words, the formula
. In other words, the formula ![]() encodes all of the algebra required to `undo’ what the formula
encodes all of the algebra required to `undo’ what the formula ![]() does to
does to ![]() . More generally, any time you have ever solved an equation, you have really been working through an inverse problem.
. More generally, any time you have ever solved an equation, you have really been working through an inverse problem.
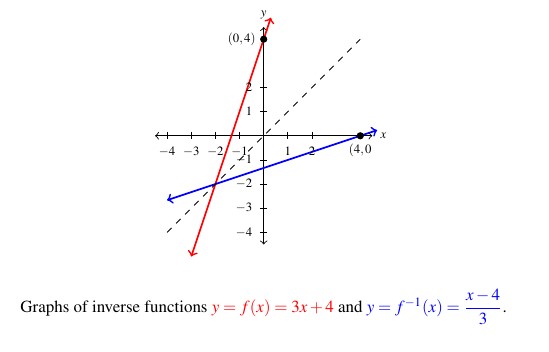
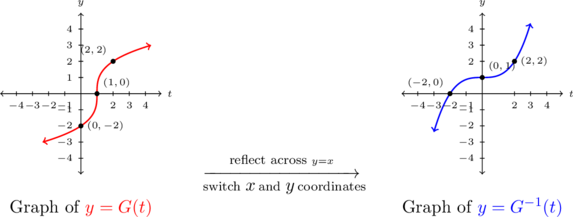
We also note the graphs of ![]() and
and ![]() are easily seen to be reflections across the line
are easily seen to be reflections across the line ![]() , as seen below. In particular, note that the
, as seen below. In particular, note that the ![]() -intercept
-intercept ![]() on the graph of
on the graph of ![]() corresponds to the
corresponds to the ![]() -intercept on the graph of
-intercept on the graph of ![]() . Indeed, the point
. Indeed, the point ![]() on the graph of
on the graph of ![]() can be interpreted as
can be interpreted as ![]() just as the point
just as the point ![]() on the graph of
on the graph of ![]() can be interpreted as
can be interpreted as ![]() .
.
Example 5.1.1
Example 5.1.1.1
For each pair of functions ![]() and
and ![]() below:
below:
![]() and
and ![]()
- Verify each pair of functions
 and
and  are inverses: (a) algebraically and (b) graphically.
are inverses: (a) algebraically and (b) graphically. - Use the fact
 and
and  are inverses to solve
are inverses to solve 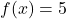 and
and 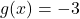
Solution:
Solution for ![]() and
and ![]() .
.
-
- (a) To verify
![Rendered by QuickLaTeX.com f(x) = \sqrt[3]{x-1} + 2](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-65f05cefea62582f8010fa7c250868fa_l3.png) and
and 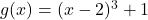 are inverses, we appeal to Definition 5.1 and show
are inverses, we appeal to Definition 5.1 and show 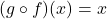 and
and 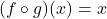 for all real numbers,
for all real numbers,  .
.
![Rendered by QuickLaTeX.com \[\begin{array}{lcl} \begin{array}{rcl} (g \circ f)(x) & = & g(f(x)) \\ & = & g(\sqrt[3]{x-1} + 2) \\ & = & [ (\sqrt[3]{x-1} + 2)-2]^3 + 1 \\ & = & (\sqrt[3]{x-1})^3 + 1 \\ & = & x-1+1 \\ & = & x \, \, \checkmark \\ \end{array} & \qquad & \begin{array}{rcl} (f \circ g)(x) & = & f(g(x)) \\ & = & f((x-2)^3+1) \\ & = & \sqrt[3]{[(x-2)^3+1] -1}+2 \\ & = & \sqrt[3]{(x-2)^3} +2\\ & = & x-4+4 \\ & = & x \, \, \checkmark \\ \end{array} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-316c2600610482ec83d0a1fcfd981cf8_l3.png)
As the root here,
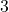 , is odd, Theorem 4.2 gives
, is odd, Theorem 4.2 gives ![Rendered by QuickLaTeX.com (\sqrt[3]{x-1})^3 = x-1](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-0d68fbf4e37c56a1af2ca0ebdd1bfe60_l3.png) and
and ![Rendered by QuickLaTeX.com \sqrt[3]{(x-2)^3} = x-2](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e5f9bf12cb72eb389522a64676daa3d9_l3.png) .
.
(b) To show and
and  are inverses graphically, we graph
are inverses graphically, we graph 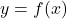 and
and 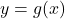 on the same set of axes and check to see if they are reflections about the line
on the same set of axes and check to see if they are reflections about the line 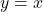 .
.
The graph of![Rendered by QuickLaTeX.com y = f(x) = \sqrt[3]{x-1} + 2](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-af5303b82e63871942f90c554a00e6d0_l3.png) appears below on the left courtesy of Theorem 4.1 in Section 4.1. The graph of
appears below on the left courtesy of Theorem 4.1 in Section 4.1. The graph of 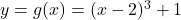 appears below in the middle thanks to Theorem 2.2 in Section 2.2.
appears below in the middle thanks to Theorem 2.2 in Section 2.2.
We can immediately see three pairs of corresponding points: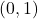 and
and 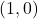 ,
, 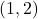 and
and 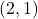 ,
, 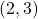 and
and 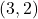 . When graphed on the same pair of axes, the two graphs certainly appear to be symmetric about the line
. When graphed on the same pair of axes, the two graphs certainly appear to be symmetric about the line 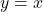 , as required.
, as required.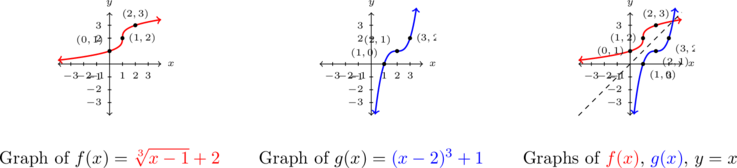
 and
and  are inverses, so the solution to
are inverses, so the solution to 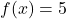 is
is 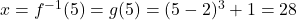 . To check, we find
. To check, we find ![Rendered by QuickLaTeX.com f(28) = \sqrt[3]{28-1}+2 = \sqrt[3]{27} + 2 = 3+2 = 5](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-8546a3ab884ee6a4964666ae9dd573da_l3.png) , as required.
, as required.
Likewise, the solution to is
is ![Rendered by QuickLaTeX.com x = g^{-1}(-3) = f(-3) = \sqrt[3]{(-3)-1} + 2 = 2 - \sqrt[3]{4}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-156643bbca0a956ddfebc1cf110f9a21_l3.png) . Once again, to check, we find
. Once again, to check, we find ![Rendered by QuickLaTeX.com g(2 - \sqrt[3]{4}) = (2 - \sqrt[3]{4}-2)^3 + 1 = (-\sqrt[3]{4})^3 +1 = -4+1 = -3](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-6d523b408a8aec7a6ac378f0e5081ed3_l3.png) .
.
- (a) To verify
Example 5.1.1.2
For each pair of functions ![]() and
and ![]() below:
below:
![]() and
and ![]()
- Verify each pair of functions
 and
and  are inverses: (a) algebraically and (b) graphically.
are inverses: (a) algebraically and (b) graphically. - Use the fact
 and
and  are inverses to solve
are inverses to solve 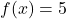 and
and 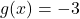
Solution:
Solution for ![]() and
and ![]() .
.
- (a) Note the domain of
 excludes
excludes 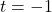 and the domain of
and the domain of  excludes
excludes 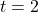 . Hence, when simplifying
. Hence, when simplifying 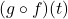 and
and 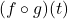 , we tacitly assume
, we tacitly assume 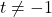 and
and 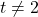 , respectively.
, respectively.
![Rendered by QuickLaTeX.com \[\begin{array}{ccc} \begin{array}{rcl} (g \circ f)(t) & = & g(f(t)) \\ [6pt] & = & g \left(\dfrac{2t}{t+1} \right) \\ [10pt] & = & \dfrac{\dfrac{2t}{t+1} }{2 - \dfrac{2t}{t+1}} \\ [25pt] & = & \dfrac{\dfrac{2t}{t+1} }{2 - \dfrac{2t}{t+1}} \cdot \dfrac{(t+1)}{(t+1)} \\ [25pt] & = & \dfrac{2t}{2(t+1) - 2t} \\ [10pt] & = & \dfrac{2t}{2t+2-2t} \\ [8pt] & = & \dfrac{2t}{2} \\ [8pt] & = & t \, \, \checkmark \\ \end{array} & \qquad & \begin{array}{rcl} (g \circ f)(t) & = & g(f(t)) \\ [6pt] & = & g \left(\dfrac{2t}{t+1} \right) \\ [10pt] & = & \dfrac{\dfrac{2t}{t+1} }{2 - \dfrac{2t}{t+1}} \\ [25pt] & = & \dfrac{\dfrac{2t}{t+1} }{2 - \dfrac{2t}{t+1}} \cdot \dfrac{(t+1)}{(t+1)} \\ [25pt] & = & \dfrac{2t}{2(t+1) - 2t} \\ [10pt] & = & \dfrac{2t}{2t+2-2t} \\ [8pt] & = & \dfrac{2t}{2} \\ [8pt] & = & t \, \, \checkmark \\ \end{array} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9fc2ccb071628dedeae9b988e8b4e97a_l3.png)
(b) We graph
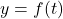 and
and 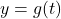 using the techniques discussed in Sections 3.2 and 3.3.
using the techniques discussed in Sections 3.2 and 3.3.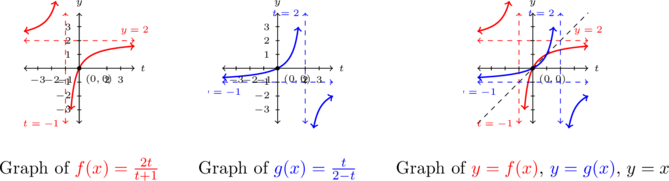
We find the graph of
 has a vertical asymptote
has a vertical asymptote  and a horizontal asymptote
and a horizontal asymptote 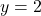 . Corresponding to the vertical asymptote
. Corresponding to the vertical asymptote 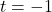 on the graph of
on the graph of  , we find the graph of
, we find the graph of  has a horizontal asymptote
has a horizontal asymptote 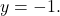
Likewise, the horizontal asymptote
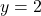 on the graph of
on the graph of  corresponds to the vertical asymptote
corresponds to the vertical asymptote 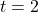 on the graph of
on the graph of  . Both graphs share the intercept
. Both graphs share the intercept 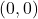 . When graphed together on the same set of axes, the graphs of
. When graphed together on the same set of axes, the graphs of  and
and  do appear to be symmetric about the line
do appear to be symmetric about the line 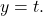
- Don’t let the fact that
 and
and  in this case were defined using the independent variable, `
in this case were defined using the independent variable, ` ‘ instead of `
‘ instead of ` ‘ deter you in your efforts to solve
‘ deter you in your efforts to solve 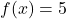 . Remember that, ultimately, the function
. Remember that, ultimately, the function  here is the process represented by the formula
here is the process represented by the formula 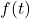 , and is the same process (with the same inverse!) regardless of the letter used as the independent variable. Hence, the solution to
, and is the same process (with the same inverse!) regardless of the letter used as the independent variable. Hence, the solution to 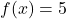 is
is 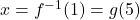 . We get
. We get 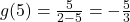 .
.
To check, we find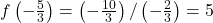 . Similarly, we solve
. Similarly, we solve 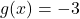 by finding
by finding 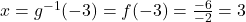 . Sure enough, we find
. Sure enough, we find 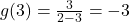 .
.
We now investigate under what circumstances a function is invertible. As a way to motivate the discussion, we consider ![]() . A likely candidate for the inverse is the function
. A likely candidate for the inverse is the function ![]() . However,
. However, ![]() , which is not equal to
, which is not equal to ![]() unless
unless ![]() . For example, when
. For example, when ![]() ,
, ![]() , but
, but ![]() . That is,
. That is, ![]() failed to return the input
failed to return the input ![]() from its output
from its output ![]() . Instead,
. Instead, ![]() matches the output
matches the output ![]() to a different input, namely
to a different input, namely ![]() , which satisfies
, which satisfies ![]() . Schematically:
. Schematically:
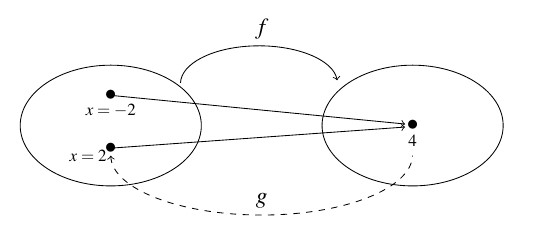
We see from the diagram that both ![]() and
and ![]() are
are ![]() , thus it is impossible to construct a function which takes
, thus it is impossible to construct a function which takes ![]() back to both
back to both ![]() and
and ![]() . Recall that by definition, a function can match
. Recall that by definition, a function can match ![]() with only one number.
with only one number.
In general, in order for a function to be invertible, each output can come from only one input. By definition, a function matches up each input to only one output, thus invertible functions have the property that they match one input to one output and vice-versa. We formalize this concept below.
Definition 5.2
A function ![]() is said to be one-to-one if whenever
is said to be one-to-one if whenever ![]() , then
, then ![]()
Note that an equivalent way to state Definition 5.2 is that a function is one-to-one if different inputs go to different outputs. That is, if ![]() , then
, then ![]()
Before we solidify the connection between invertible functions and one-to-one functions, we take a moment to see what goes wrong graphically when trying to find the inverse of ![]() .
.
Per Theorem 5.1, the graph of ![]() , if it exists, is obtained from the graph of
, if it exists, is obtained from the graph of ![]() by reflecting
by reflecting ![]() about the line
about the line ![]() . Procedurally, this is accomplished by interchanging the
. Procedurally, this is accomplished by interchanging the ![]() and
and ![]() coordinates of each point on the graph of
coordinates of each point on the graph of ![]() . Algebraically, we are swapping the variables `
. Algebraically, we are swapping the variables `![]() ‘ and `
‘ and `![]() ‘ which results in the equation
‘ which results in the equation ![]() whose graph is below on the right.
whose graph is below on the right.

We see immediately the graph of ![]() fails the Vertical Line Test, Theorem 1.2. In particular, the vertical line
fails the Vertical Line Test, Theorem 1.2. In particular, the vertical line ![]() intersects the graph at two points,
intersects the graph at two points, ![]() and
and ![]() meaning the relation described by
meaning the relation described by ![]() matches the
matches the ![]() -value
-value ![]() with two different
with two different ![]() -values,
-values, ![]() and
and ![]() .
.
Note that the vertical line ![]() and the points
and the points ![]() on the graph of
on the graph of ![]() correspond to the horizontal line
correspond to the horizontal line ![]() and the points
and the points ![]() on the graph of
on the graph of ![]() which brings us right back to the concept of one-to-one. The fact that both
which brings us right back to the concept of one-to-one. The fact that both ![]() and
and ![]() are on the graph of
are on the graph of ![]() means
means ![]() . Hence,
. Hence, ![]() takes different inputs,
takes different inputs, ![]() and
and ![]() , to the same output,
, to the same output, ![]() , so
, so ![]() is not one-to-one.
is not one-to-one.
Recall the Horizontal Line Test from Exercise57 in Section 1.2. Applying that result to the graph of ![]() we say the graph of
we say the graph of ![]() `fails’ the Horizontal Line Test because the horizontal line
`fails’ the Horizontal Line Test because the horizontal line ![]() intersects the graph of
intersects the graph of ![]() more than once. This means that the equation
more than once. This means that the equation ![]() does not represent
does not represent ![]() as a function of
as a function of ![]() .
.
Said differently, the Horizontal Line Test detects when there is at least one ![]() -value (
-value (![]() ) which is matched to more than one
) which is matched to more than one ![]() -value (
-value (![]() ). In other words, the Horizontal Line Test can be used to detect whether or not a function is one-to-one.
). In other words, the Horizontal Line Test can be used to detect whether or not a function is one-to-one.
So, to review, ![]() is not invertible, not one-to-one, and its graph fails the Horizontal Line Test. It turns out that these three attributes: being invertible, one-to-one, and having a graph that passes the Horizontal Line Test are mathematically equivalent. That is to say if one if these things is true about a function, then they all are; it also means that, as in this case, if one of these things isn’t true about a function, then none of them are. We summarize this result in the following theorem.
is not invertible, not one-to-one, and its graph fails the Horizontal Line Test. It turns out that these three attributes: being invertible, one-to-one, and having a graph that passes the Horizontal Line Test are mathematically equivalent. That is to say if one if these things is true about a function, then they all are; it also means that, as in this case, if one of these things isn’t true about a function, then none of them are. We summarize this result in the following theorem.
Theorem 5.2 Equivalent Conditions for Invertibility
For a function ![]() , either all of the following statements are true or none of them are:
, either all of the following statements are true or none of them are:
 is invertible.
is invertible.- The graph of
 passes the Horizontal Line Test.[5]
passes the Horizontal Line Test.[5]
To prove Theorem 5.2, we first suppose ![]() is invertible. Then there is a function
is invertible. Then there is a function ![]() so that
so that ![]() for all
for all ![]() in the domain of
in the domain of ![]() . If
. If ![]() , then
, then ![]() . As a result of
. As a result of ![]() , the equation
, the equation ![]() reduces to
reduces to ![]() . We’ve shown that if
. We’ve shown that if ![]() , then
, then ![]() , proving
, proving ![]() is one-to-one.
is one-to-one.
Next, assume ![]() is one-to-one. Suppose a horizontal line
is one-to-one. Suppose a horizontal line ![]() intersects the graph of
intersects the graph of ![]() at the points
at the points ![]() and
and ![]() . This means
. This means ![]() and
and ![]() so
so ![]() . Because
. Because ![]() is one-to-one, means
is one-to-one, means ![]() so the points
so the points ![]() and
and ![]() are actually one in the same. This establishes that each horizontal line can intersect the graph of
are actually one in the same. This establishes that each horizontal line can intersect the graph of ![]() at most once, so the graph of
at most once, so the graph of ![]() passes the Horizontal Line Test.
passes the Horizontal Line Test.
Last, but not least, suppose the graph of ![]() passes the Horizontal Line Test. Let
passes the Horizontal Line Test. Let ![]() be a real number in the range of
be a real number in the range of ![]() . Then the horizontal line
. Then the horizontal line ![]() intersects the graph of
intersects the graph of ![]() just once, say at the point
just once, say at the point ![]() . Define the mapping
. Define the mapping ![]() so that
so that ![]() . The mapping
. The mapping ![]() is a function because each horizontal line
is a function because each horizontal line ![]() where
where ![]() is in the range of
is in the range of ![]() intersects the graph of
intersects the graph of ![]() only once. By construction, we have the domain of
only once. By construction, we have the domain of ![]() is the range of
is the range of ![]() and that for all
and that for all ![]() in the domain of
in the domain of ![]() ,
, ![]() . We leave it to the reader to show that for all
. We leave it to the reader to show that for all ![]() in the domain of
in the domain of ![]() ,
, ![]() , too.
, too.
Hence, we’ve shown: first, if ![]() invertible, then
invertible, then ![]() is one-to-one; second, if
is one-to-one; second, if ![]() is one-to-one, then the graph of
is one-to-one, then the graph of ![]() passes the Horizontal Line Test; and third, if
passes the Horizontal Line Test; and third, if ![]() passes the Horizontal Line Test, then
passes the Horizontal Line Test, then ![]() is invertible. Therefore if
is invertible. Therefore if ![]() is satisfies any one of these three conditions, then
is satisfies any one of these three conditions, then ![]() must satisfy the other two.[6]
must satisfy the other two.[6]
We put this result to work in the next example.
Example 5.1.2
Example 5.1.2.1
Determine if the following functions are one-to-one:
- analytically using Definition 5.2 and
- graphically using the Horizontal Line Test.
For the functions that are one-to-one, graph the inverse.
![]()
Solution:
Determine if ![]() is a one-to-one function.
is a one-to-one function.
- To determine whether or not
 is one-to-one analytically, we assume
is one-to-one analytically, we assume 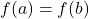 and work to see if we can deduce
and work to see if we can deduce 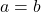 . As we work our way through the problem, we encounter a quadratic equation. We rewrite the equation so it equals
. As we work our way through the problem, we encounter a quadratic equation. We rewrite the equation so it equals  and factor by grouping. We get
and factor by grouping. We get 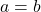 as one possibility, but we also get the possibility that
as one possibility, but we also get the possibility that 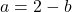 . This suggests that
. This suggests that  may not be one-to-one. Taking
may not be one-to-one. Taking 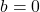 , we get
, we get 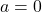 or
or 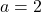 . We have two different inputs with the same output as
. We have two different inputs with the same output as 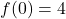 and
and 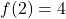 , proving
, proving  is neither one-to-one nor invertible.
is neither one-to-one nor invertible.
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f(a) & = & f(b) \\ a^2 - 2a+4 & = & b^2 - 2b+4 \\ a^2 - 2a & = & b^2 - 2b \\ a^2 - b^2 - 2a + 2b & = & 0 \\ (a+b)(a-b) - 2(a-b) & = & 0 \\ (a-b)((a+b) -2) & = & 0 \\ a-b = 0 & \text{or} & a+b -2 = 0 \\ a = b & \text{or} & a = 2-b \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5a93f67ca9b54ac071341e07ef467ad3_l3.png)
- We note that
 is a quadratic function and we graph
is a quadratic function and we graph 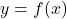 using the techniques presented in Section 2.1. We see the graph fails the Horizontal Line Test quite often – in particular, crossing the line
using the techniques presented in Section 2.1. We see the graph fails the Horizontal Line Test quite often – in particular, crossing the line 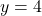 at the points
at the points 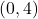 and
and 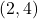 .
.

Example 5.1.2.2
Determine if the following functions are one-to-one:
- analytically using Definition 5.2 and
- graphically using the Horizontal Line Test.
For the functions that are one-to-one, graph the inverse.
![]()
Solution:
Determine if ![]() is a one-to-one function.
is a one-to-one function.
- We begin with the assumption that
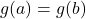 for
for  ,
,  in the domain of
in the domain of  (That is, we assume
(That is, we assume 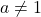 and
and 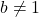 .) Through our work, we deduce
.) Through our work, we deduce 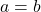 , proving
, proving  is one-to-one.
is one-to-one.
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(a) & = & g(b) \\ [3pt] \dfrac{2a}{1-a} & = & \dfrac{2b}{1-b} \\ [6pt] 2a(1-b) & = & 2b(1-a) \\ 2a - 2ab & = & 2b - 2ba \\ 2a & = & 2b \\ a & = & b \, \, \checkmark \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-073b399f2e885be83949c17759fbddc7_l3.png)
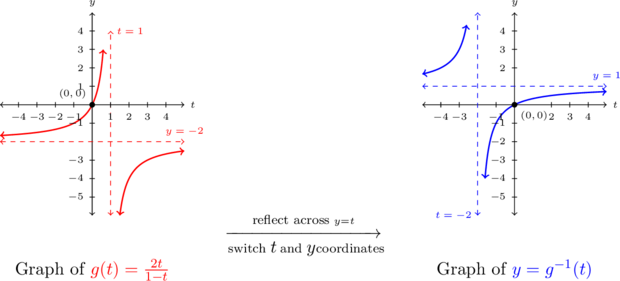
- We graph
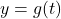 using the procedure outlined in Section 3.3. We find the sole intercept is
using the procedure outlined in Section 3.3. We find the sole intercept is 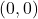 with asymptotes
with asymptotes 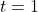 and
and 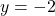 . Based on our graph, the graph of
. Based on our graph, the graph of  appears to pass the Horizontal Line Test, verifying
appears to pass the Horizontal Line Test, verifying  is one-to-one.
is one-to-one.
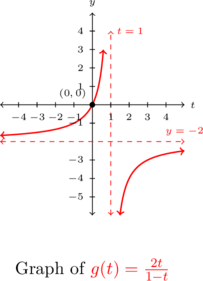
Because
 is one-to-one,
is one-to-one,  is invertible. Even though we do not have a formula for
is invertible. Even though we do not have a formula for 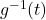 , we can nevertheless sketch the graph of
, we can nevertheless sketch the graph of 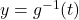 by reflecting the graph of
by reflecting the graph of 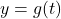 across
across 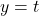 .
.Corresponding to the vertical asymptote
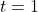 on the graph of
on the graph of  , the graph of
, the graph of 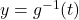 will have a horizontal asymptote
will have a horizontal asymptote 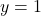 . Similarly, the horizontal asymptote
. Similarly, the horizontal asymptote 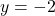 on the graph of
on the graph of  corresponds to a vertical asymptote
corresponds to a vertical asymptote 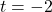 on the graph of
on the graph of 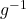 . The point
. The point 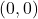 remains unchanged when we switch the
remains unchanged when we switch the  and
and  coordinates, so it is on both the graph of
coordinates, so it is on both the graph of  and
and 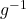 .
.
Example 5.1.2.3
Determine if the following functions are one-to-one:
- analytically using Definition 5.2 and
- graphically using the Horizontal Line Test.
For the functions that are one-to-one, graph the inverse.
![]()
Solution:
Determine if ![]() is a one-to-one function.
is a one-to-one function.
- The function
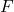 is given to us as a set of ordered pairs. Recall each ordered pair is of the form
is given to us as a set of ordered pairs. Recall each ordered pair is of the form 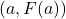 . As
. As 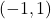 and
and 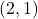 are both elements of
are both elements of 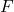 , this means
, this means 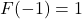 and
and 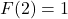 .
.
Hence, we have two distinct inputs,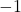 and
and 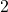 with the same output,
with the same output, 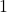 , thus
, thus 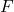 is not one-to-one and, hence, not invertible.
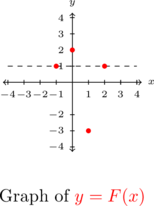
is not one-to-one and, hence, not invertible. - To graph
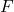 , we plot the points in
, we plot the points in 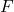 below on the left. We see the horizontal line
below on the left. We see the horizontal line 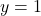 crosses the graph more than once. Hence, the graph of
crosses the graph more than once. Hence, the graph of 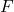 fails the Horizontal Line Test.
fails the Horizontal Line Test.
Example 5.1.2.4
Determine if the following functions are one-to-one:
- analytically using Definition 5.2 and
- graphically using the Horizontal Line Test.
For the functions that are one-to-one, graph the inverse.
![]()
Solution:
Determine if ![]() is a one-to-one function.
is a one-to-one function.
Like the function ![]() above, the function
above, the function ![]() is described as a set of ordered pairs. Before we set about determining whether or not
is described as a set of ordered pairs. Before we set about determining whether or not ![]() is one-to-one, we take a moment to show
is one-to-one, we take a moment to show ![]() is, in fact, a function. That is, we must show that each real number input to
is, in fact, a function. That is, we must show that each real number input to ![]() is matched to only one output.
is matched to only one output.
We are given ![]() . and we know that when represented in this way, each ordered pair is of the form (input, output). Hence, the inputs to
. and we know that when represented in this way, each ordered pair is of the form (input, output). Hence, the inputs to ![]() are of the form
are of the form ![]() and the outputs from
and the outputs from ![]() are of the form
are of the form ![]() . To establish
. To establish ![]() is a function, we must show that each input produces only one output. If it should happen that
is a function, we must show that each input produces only one output. If it should happen that ![]() , then we must show
, then we must show ![]() . The equation
. The equation ![]() gives
gives ![]() , or
, or ![]() . From this it follows that
. From this it follows that ![]() so
so ![]() is a function.
is a function.
- To show
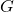 is one-to-one, we must show that if two outputs from
is one-to-one, we must show that if two outputs from 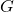 are the same, the corresponding inputs must also be the same. That is, we must show that if
are the same, the corresponding inputs must also be the same. That is, we must show that if 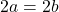 , then
, then 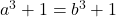 . We see almost immediately that if
. We see almost immediately that if 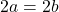 then
then 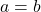 so
so 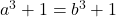 as required. This shows
as required. This shows 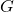 is one-to-one and, hence, invertible.
is one-to-one and, hence, invertible. - We graph
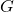 below on the left by plotting points in the default
below on the left by plotting points in the default 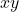 -plane by choosing different values for
-plane by choosing different values for  . For instance,
. For instance, 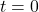 corresponds to the point
corresponds to the point 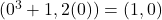 ,
, 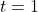 corresponds to the point
corresponds to the point 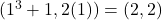 ,
, 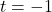 corresponds to the point
corresponds to the point 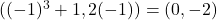 , etc. Our graph appears to pass the Horizontal Line Test, confirming
, etc. Our graph appears to pass the Horizontal Line Test, confirming 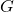 is one-to-one. We obtain the graph of
is one-to-one. We obtain the graph of 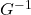 below on the right by reflecting the graph of
below on the right by reflecting the graph of 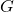 about the line
about the line 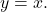
In Example 5.1.2, we showed the functions ![]() and
and ![]() are invertible and graphed their inverses. While graphs are perfectly fine representations of functions, we have seen where they aren’t the most accurate. Ideally, we would like to represent
are invertible and graphed their inverses. While graphs are perfectly fine representations of functions, we have seen where they aren’t the most accurate. Ideally, we would like to represent ![]() and
and ![]() in the same manner in which
in the same manner in which ![]() and
and ![]() are presented to us. The key to doing this is to recall that inverse functions take outputs back to their associated inputs.
are presented to us. The key to doing this is to recall that inverse functions take outputs back to their associated inputs.
Consider ![]() . As mentioned in Example 5.1.2, the ordered pairs which comprise
. As mentioned in Example 5.1.2, the ordered pairs which comprise ![]() are in the form (input, output). Hence to find a compatible description for
are in the form (input, output). Hence to find a compatible description for ![]() , we simply interchange the expressions in each of the coordinates to obtain
, we simply interchange the expressions in each of the coordinates to obtain ![]() .
.
The function ![]() was defined in terms of a formula, so we would like to find a formula representation for
was defined in terms of a formula, so we would like to find a formula representation for ![]() . We apply the same logic as above. Here, the input, represented by the independent variable
. We apply the same logic as above. Here, the input, represented by the independent variable ![]() , and the output, represented by the dependent variable
, and the output, represented by the dependent variable ![]() , are related by the equation
, are related by the equation ![]() . Hence, to exchange inputs and outputs, we interchange the `
. Hence, to exchange inputs and outputs, we interchange the `![]() ‘ and `
‘ and `![]() ‘ variables. Doing so, we obtain the equation
‘ variables. Doing so, we obtain the equation ![]() which is an implicit description for
which is an implicit description for ![]() . Solving for
. Solving for ![]() gives an explicit formula for
gives an explicit formula for ![]() , namely
, namely ![]() . We demonstrate this technique below.
. We demonstrate this technique below.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} y & = & g(t) & \\ [5pt] y & = & \dfrac{2t}{1-t} & \\ [7pt] t & = & \dfrac{2y}{1-y} & \text{interchange variables: } t \text{ and } y \\ [3pt] t(1-y) & = & 2y & \\ [3pt] t-ty & = & 2y & \\ [3pt] t & = & ty + 2y & \\ [3pt] t & = & y(t+2) & \text{factor}\\ [8pt] y & = & \dfrac{t}{t+2} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-254103ba34f9bc364e129d9b30983ccc_l3.png)
We claim ![]() , and leave the algebraic verification of this to the reader.
, and leave the algebraic verification of this to the reader.
We generalize this approach below. As always, we resort to the default `![]() ‘ and `
‘ and `![]() ‘ labels for the independent and dependent variables, respectively.
‘ labels for the independent and dependent variables, respectively.
Steps for finding a formula for the inverse of a one-to-one function
- Write
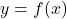
- Interchange
 and
and 
- Solve
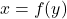 for
for  to obtain
to obtain 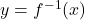
We now return to ![]() . We know that
. We know that ![]() is not one-to-one, and thus, is not invertible, but our goal here is to see what goes wrong algebraically.
is not one-to-one, and thus, is not invertible, but our goal here is to see what goes wrong algebraically.
If we attempt to follow the algorithm above to find a formula for ![]() , we start with the equation
, we start with the equation ![]() and interchange the variables `
and interchange the variables `![]() ‘ and `
‘ and `![]() ‘ to produce the equation
‘ to produce the equation ![]() . Solving for
. Solving for ![]() gives
gives ![]() It’s this `
It’s this `![]() ‘ which is causing the problem for us as this produces two
‘ which is causing the problem for us as this produces two ![]() -values for any
-values for any ![]()
Using the language of Section 1.2, the equation ![]() implicitly defines two functions,
implicitly defines two functions, ![]() and
and ![]() , each of which represents the top and bottom halves, respectively, of the graph of
, each of which represents the top and bottom halves, respectively, of the graph of ![]()
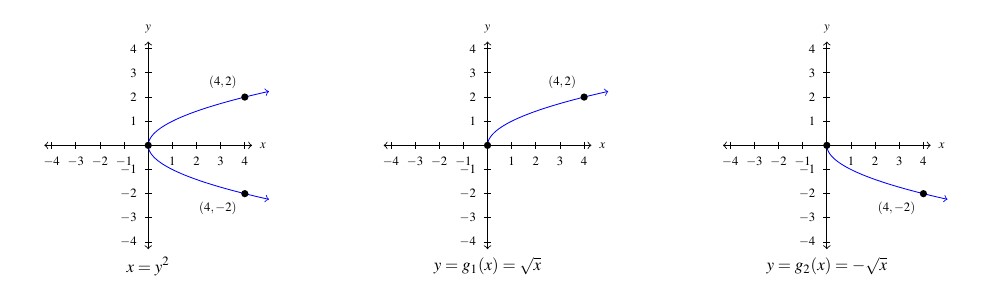
Hence, in some sense, we have two partial inverses for ![]() :
: ![]() returns the positive inputs from
returns the positive inputs from ![]() and
and ![]() returns the negative inputs to
returns the negative inputs to ![]() . In order to view each of these functions as strict inverses, however, we need to split
. In order to view each of these functions as strict inverses, however, we need to split ![]() into two parts:
into two parts: ![]() for
for ![]() and
and ![]() for
for ![]() .
.
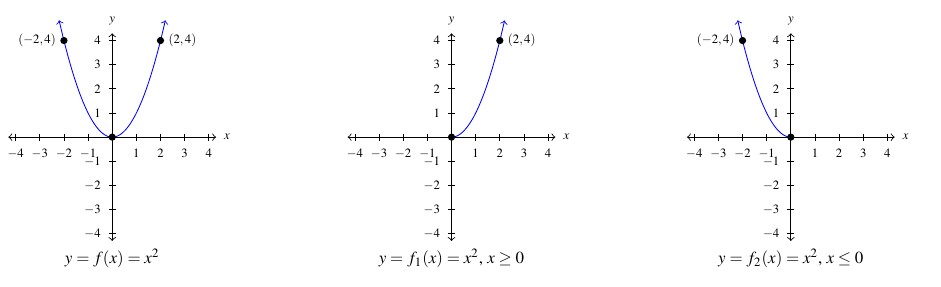
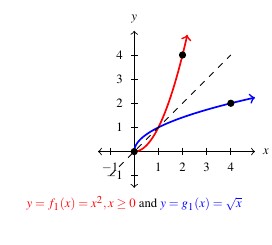
We claim that ![]() and
and ![]() are an inverse function pair as are
are an inverse function pair as are ![]() and
and ![]() . Indeed, we find:
. Indeed, we find:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \begin{array}{rcl} (g_{1} \circ f_{1})(x) & = & g_{1}(f_{1}(x)) \\ & = & g_{1}(x^2) \\ & = & \sqrt{x^2} \\ & = & |x| = x, \, \text{as $x \geq 0$.} \\ \end{array} & \qquad \qquad & \begin{array}{rcl} (f_{1} \circ g_{1})(x) & = & f_{1}(g_{1}(x)) \\ & = & f_{1}(\sqrt{x}) \\ & = & (\sqrt{x})^2 \\ & = & x \\ \end{array} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d86762f8d4a62b7eca6a9ceb69bdf157_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \begin{array}{rcl} (g_{2} \circ f_{2})(x) & = & g_{2}(f_{2}(x)) \\ & = & g_{2}(x^2) \\ & = & -\sqrt{x^2} \\ & = & - |x| \\ & = & -(-x) = x, \, \text{as $x \leq 0$.} \end{array} & \qquad \qquad & \begin{array}{rcl} (f_{2} \circ g_{2})(x) & = & f_{2}(g_{2}(x)) \\ & = & f_{2}(-\sqrt{x}) \\ & = & (-\sqrt{x})^2 \\ & = & (\sqrt{x})^2 \\ & = & x \\ \end{array} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-370b3168e7b1265d60ac4ea53e746856_l3.png)
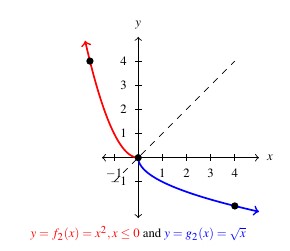
Hence, by restricting the domain of ![]() we are able to produce invertible functions. Said differently, because the equation
we are able to produce invertible functions. Said differently, because the equation ![]() implicitly describes a pair of functions, the equation
implicitly describes a pair of functions, the equation ![]() implicitly describes a pair of invertible functions.
implicitly describes a pair of invertible functions.
Our next example continues the theme of restricting the domain of a function to find inverse functions.
Example 5.1.3
Example 5.1.3.1
Graph the following functions to show they are one-to-one and determine their inverses. Check your answers analytically using function composition and graphically.
![]() ,
, ![]()
Solution:
Graph ![]() ,
, ![]() to show it is one-to-one and determine its inverse.
to show it is one-to-one and determine its inverse.
The function ![]() is a restriction of the function
is a restriction of the function ![]() from Example 5.1.2. The domain of
from Example 5.1.2. The domain of ![]() is restricted to
is restricted to ![]() , therefore we are selecting only the `left half’ of the parabola. Hence, the graph of
, therefore we are selecting only the `left half’ of the parabola. Hence, the graph of ![]() , seen below, passes the Horizontal Line Test and thus
, seen below, passes the Horizontal Line Test and thus ![]() is invertible.
is invertible.
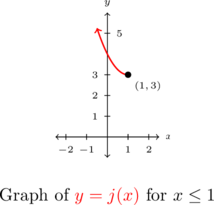
Next, we find an explicit formula for ![]() using our standard algorithm.[7]
using our standard algorithm.[7]
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} y & = & j(x) & \\ y & = & x^2-2x+4, \, \, \, x \leq 1 \\ x & = & y^2 - 2y+4, \, \, \, y \leq 1 & \text{switch } x \text{ and } y \\ 0 & = & y^2 - 2y + 4-x & \\ y & = & \dfrac{2 \pm \sqrt{(-2)^2-4(1)(4-x)}}{2(1)} & \text{quadratic formula, } c=4-x \\ [10pt] y & = & \dfrac{2 \pm \sqrt{4x-12}}{2} & \\ [6pt] y & = & \dfrac{2 \pm \sqrt{4(x-3)}}{2} & \\ [6pt] y & = & \dfrac{2 \pm 2\sqrt{x-3}}{2} & \\ [6pt] y & = & \dfrac{2\left(1 \pm \sqrt{x-3}\right)}{2} & \\ [6pt] y & = & 1 \pm \sqrt{x-3} & \\ y & = & 1 - \sqrt{x-3} & \text{due to the fact that } y \leq 1 \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-6e663ba1de2d9396d794126308441147_l3.png)
Hence, ![]() .
.
To check our answer algebraically, we simplify ![]() and
and ![]() Note the importance of the domain restriction
Note the importance of the domain restriction ![]() when simplifying
when simplifying ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \left(j^{-1} \circ j \right)(x) & = & j^{-1}(j(x)) \\ & = & j^{-1}\left(x^2-2x+4\right), \, \, \, x \leq 1 \\ & = & 1 - \sqrt{\left(x^2-2x+4\right)-3} \\ & = & 1 - \sqrt{x^2-2x+1} \\ & = & 1 - \sqrt{(x-1)^2} \\ & = & 1 - |x-1| \\ & = & 1 - (-(x-1)) \, \, \text{as $x \leq 1$}\\ & = & x \, \, \checkmark \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-1764791f8bde16c7c70a825a9d2d2531_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \left(j \circ j^{-1} \right)(x) & = & j\left(j^{-1}(x)\right) \\ & = & j\left(1 - \sqrt{x-3}\right) \\ & = & \left(1 - \sqrt{x-3}\right)^2-2\left(1 - \sqrt{x-3}\right)+4 \\ & = & 1 - 2\sqrt{x-3} + \left(\sqrt{x-3}\right)^2 -2 \\ & & + \, 2\sqrt{x-3}+4 \\ & = & 1+ x-3 -2 +4 \\ & = & x \, \, \checkmark \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f9fdc20e40c296d83d49351d07ea0140_l3.png)
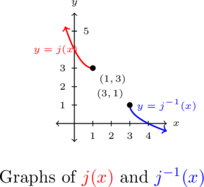
We graph both ![]() and
and ![]() on the axes below. They appear to be symmetric about the line
on the axes below. They appear to be symmetric about the line ![]() .
.
Example 5.1.3.2
Graph the following functions to show they are one-to-one 2nd determine their inverses. Check your answers analytically using function composition and graphically.
![]()
Solution:
Graph ![]() to show it is one-to-one and determine its inverse.
to show it is one-to-one and determine its inverse.
Graphing ![]() , we see
, we see ![]() is one-to-one,
is one-to-one,
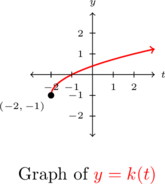
so we proceed to find an formula for ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} y & = & k(t) & \\ y & = & \sqrt{t+2}-1 & \\ t & = & \sqrt{y+2} - 1 & \text{switch $t$ and $y$} \\ t+1 & = & \sqrt{y+2} & \\ (t+1)^2 & = & \left(\sqrt{y+2}\right)^2 & \\ t^2 + 2t + 1 & = & y + 2 & \\ y & = & t^2 + 2t - 1 & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-84e7ce1207d89a744ae6fd6a1ea79dc1_l3.png)
We have ![]() . Based on our experience, we know something isn’t quite right. We determined
. Based on our experience, we know something isn’t quite right. We determined ![]() is a quadratic function, and we have seen several times in this section that these are not one-to-one unless their domains are suitably restricted.
is a quadratic function, and we have seen several times in this section that these are not one-to-one unless their domains are suitably restricted.
Theorem 5.1tells us that the domain of ![]() is the range of
is the range of ![]() . From the graph of
. From the graph of ![]() , we see that the range is
, we see that the range is ![]() , which means we restrict the domain of
, which means we restrict the domain of ![]() to
to ![]() .
.
We now check that this works in our compositions. Note the importance of the domain restriction, ![]() when simplifying
when simplifying ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \left(k^{-1} \circ k \right)(t) & = & k^{-1}(k(t)) \\ & = & k^{-1}\left(\sqrt{t+2}-1\right) \\ & = & \left(\sqrt{t+2}-1\right)^2 + 2\left(\sqrt{t+2}-1\right) - 1 \\ & = & \left(\sqrt{t+2}\right)^2 - 2\sqrt{t+2} + 1 \\ && + \, 2 \sqrt{t+2} - 2 - 1 \\ & = &t+2 -2 \\ & = & t \, \, \checkmark \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-99a467102e938d9a9c151674ebeb5011_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{rcl} \left(k \circ k^{-1} \right)(t) & = & k\left( t^2+2t-1 \right), \, \, \, t \geq -1 \\ & = & \sqrt{\left(t^2+2t-1\right)+2}-1 \\ & = & \sqrt{t^2+2t+1}-1 \\ & = & \sqrt{(t+1)^2}-1 \\ & = & |t+1| -1 \\ & = & t+1 -1, \, \, \text{as $t \geq -1$} \\ & = & t \, \, \checkmark \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-1a61689367baa9dfcf0020faf6db959f_l3.png)
Graphically, everything checks out, provided that we remember the domain restriction on ![]() means we take the right half of the parabola.
means we take the right half of the parabola.

Our last example of the section gives an application of inverse functions. Recall in Example 1.3.9 in Section 1.3.1, we modeled the demand for PortaBoy game systems as the price per system, ![]() as a function of the number of systems sold,
as a function of the number of systems sold, ![]() . In the following example, we find
. In the following example, we find ![]() and interpret what it means.
and interpret what it means.
Example 5.1.4
Example 5.1.4.1
Recall the price-demand function for PortaBoy game systems is modeled by the formula ![]() for
for ![]() where
where ![]() represents the number of systems sold (the demand) and
represents the number of systems sold (the demand) and ![]() is the price per system, in dollars.
is the price per system, in dollars.
Explain why ![]() is one-to-one and find a formula for
is one-to-one and find a formula for ![]() . State the restricted domain.
. State the restricted domain.
Solution:
Explain why ![]() is one-to-one and find a formula for
is one-to-one and find a formula for ![]() . State the restricted domain.
. State the restricted domain.
Recall the graph of ![]() ,
, ![]() , is a line segment from
, is a line segment from ![]() to
to ![]() , and as such passes the Horizontal Line Test. Hence,
, and as such passes the Horizontal Line Test. Hence, ![]() is one-to-one.
is one-to-one.
We determine the expression for ![]() as usual and get
as usual and get ![]()
The domain of ![]() should match the range of
should match the range of ![]() , which is
, which is ![]() , and as such, we restrict the domain of
, and as such, we restrict the domain of ![]() to
to ![]()
Example 5.1.4.2
Recall the price-demand function for PortaBoy game systems is modeled by the formula ![]() for
for ![]() where
where ![]() represents the number of systems sold (the demand) and
represents the number of systems sold (the demand) and ![]() is the price per system, in dollars.
is the price per system, in dollars.
Compute and interpret ![]() .
.
Solution:
Compute and interpret ![]() .
.
We find ![]() .
.
The function ![]() took as inputs the number of systems sold and returned the price per system as the output, thus
took as inputs the number of systems sold and returned the price per system as the output, thus ![]() takes the price per system as its input and returns the number of systems sold as its output.
takes the price per system as its input and returns the number of systems sold as its output.
Hence, ![]() means 20 systems will be sold if the price is set at 220 dollars per system.
means 20 systems will be sold if the price is set at 220 dollars per system.
Example 5.1.4.3
Recall the price-demand function for PortaBoy game systems is modeled by the formula ![]() for
for ![]() where
where ![]() represents the number of systems sold (the demand) and
represents the number of systems sold (the demand) and ![]() is the price per system, in dollars.
is the price per system, in dollars.
Recall from Section 2.1that the profit ![]() , in dollars, as a result of selling
, in dollars, as a result of selling ![]() systems is given by
systems is given by ![]() . Write and interpret
. Write and interpret ![]() .
.
Solution:
Write and interpret ![]() .
.
We compute
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \left( P \circ p^{-1}\right)(x) & = & P \left(p^{-1}(x)\right) \\ & = & P\left(\frac{500-2x}{3}\right) \\ & = & -1.5\left(\frac{500-2x}{3}\right)^2+170\left(\frac{500-2x}{3}\right)-150 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-ccfd9329030bb77df851c905f8dbef9d_l3.png)
After a hefty amount of algebra,[8] we obtain ![]() .
.
To understand what this means, recall that the original profit function ![]() gave us the profit as a function of the number of systems sold. The function
gave us the profit as a function of the number of systems sold. The function ![]() gives us the number of systems sold as a function of the price.
gives us the number of systems sold as a function of the price.
Hence, when we compute ![]() , we input a price per system,
, we input a price per system, ![]() into the function
into the function ![]() .
.
The number ![]() is the number of systems sold at that price. This number is then fed into
is the number of systems sold at that price. This number is then fed into ![]() to return the profit obtained by selling
to return the profit obtained by selling ![]() systems.
systems.
Hence, ![]() gives us the profit (in dollars) as a function of the price per system,
gives us the profit (in dollars) as a function of the price per system, ![]() .
.
Example 5.1.4.4
Recall the price-demand function for PortaBoy game systems is modeled by the formula ![]() for
for ![]() where
where ![]() represents the number of systems sold (the demand) and
represents the number of systems sold (the demand) and ![]() is the price per system, in dollars.
is the price per system, in dollars.
Use your answer to part 3 to determine the price per PortaBoy which would yield the maximum profit. Compare with Example 2.1.3.
Solution:
Use your answer to part 3 to determine the price per PortaBoy which would yield the maximum profit. Compare with Example 2.1.3.
We know from Section 2.1 that the graph of ![]() is a parabola opening downwards. The maximum profit is realized at the vertex. We are concerned only with the price per system, so we need only find the
is a parabola opening downwards. The maximum profit is realized at the vertex. We are concerned only with the price per system, so we need only find the ![]() -coordinate of the vertex.
-coordinate of the vertex.
Identifying ![]() and
and ![]() , we get, by the Vertex Formula, Equation 2.1,
, we get, by the Vertex Formula, Equation 2.1, ![]() .
.
Hence, the weekly profit is maximized if we set the price at 165 dollars per system. Comparing this with our answer from Example 2.1.3, there is a slight discrepancy to the tune of 50 cents. We leave it to the reader to balance the books appropriately.
5.1.1 Section Exercises
In Exercises 1 – 8, verify the given pairs of functions are inverses algebraically and graphically.
In Exercises 9 – 28, show that the given function is one-to-one and find its inverse. Check your answers algebraically and graphically. Verify the range of the function is the domain of its inverse and vice-versa.
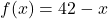
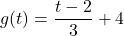
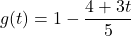
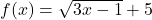
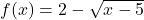
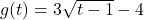
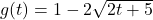
![Rendered by QuickLaTeX.com f(x) = \sqrt[5]{3x-1}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c0212e8c410768742802d1203f707166_l3.png)
![Rendered by QuickLaTeX.com f(x) = 3-\sqrt[3]{x-2}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f06b094672d281ba4818510956f1e474_l3.png)
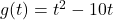 ,
, 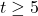
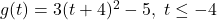
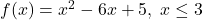
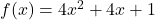 ,
, 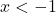
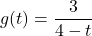
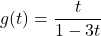
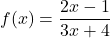
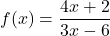
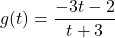
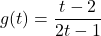
- Explain why each set of ordered pairs below represents a one-to-one function and find the inverse.
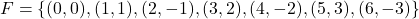
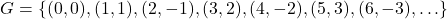 NOTE: The difference between
NOTE: The difference between  and
and  is the `
is the ` .’
.’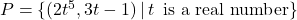
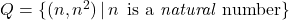 [9]
[9]
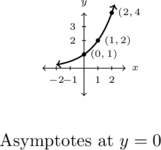
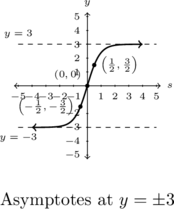
In Exercises 30 – 33, explain why each graph represents[10] a one-to-one function and graph its inverse.
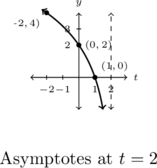
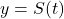
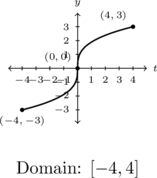
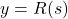
- The price of a dOpi media player, in dollars per dOpi, is given as a function of the weekly sales
 according to the formula
according to the formula 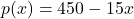 for
for 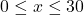 .
.
- Find
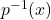 and state its domain.
and state its domain. - Compute and interpret
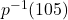 .
. - The profit (in dollars) made from producing and selling
 dOpis per week is given by the formula
dOpis per week is given by the formula 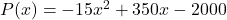 , for
, for 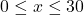 . Find
. Find 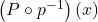 and determine what price per dOpi would yield the maximum profit. What is the maximum profit? How many dOpis need to be produced and sold to achieve the maximum profit?
and determine what price per dOpi would yield the maximum profit. What is the maximum profit? How many dOpis need to be produced and sold to achieve the maximum profit?
- Find
- Show that the Fahrenheit to Celsius conversion function found in Exercise 67 in Section1.3.3 is invertible and that its inverse is the Celsius to Fahrenheit conversion function.
- Analytically show that the function
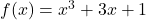 is one-to-one. Use Theorem 5.1 to help you compute
is one-to-one. Use Theorem 5.1 to help you compute 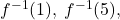 and
and 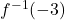 . What happens when you attempt to find a formula for
. What happens when you attempt to find a formula for 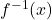 ?
? - Let
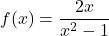 .
.
- Graph
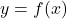 using the techniques in Section 3.3. Check your answer using a graphing utility.
using the techniques in Section 3.3. Check your answer using a graphing utility. - Verify that
 is one-to-one on the interval
is one-to-one on the interval 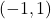 .
. - Use the procedure outlined in this section to find the formula for
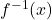 for
for 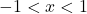 .
. - Because
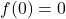 , it should be the case that
, it should be the case that 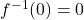 . What goes wrong when you attempt to substitute
. What goes wrong when you attempt to substitute 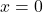 into
into 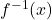 ? Discuss with your classmates how this problem arose and possible remedies.
? Discuss with your classmates how this problem arose and possible remedies.
- Graph
- The function given in number 4 is an example of a function which is its own inverse.
- Algebraically verify every function of the form:
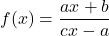 is its own inverse.What assumptions do you need to make about the values of
is its own inverse.What assumptions do you need to make about the values of  ,
,  , and
, and  ?
? - Under what conditions is
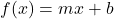 ,
, 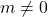 its own inverse? Prove your answer.
its own inverse? Prove your answer.
- Algebraically verify every function of the form:
Section 5.1 Exercise Answers can be found in the Appendix … Coming soon
- At the level of functions,
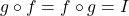 , where
, where 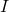 is the identity function as defined as
is the identity function as defined as 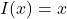 for all real numbers,
for all real numbers,  . ↵
. ↵ - The identity function
 , first introduced in Exercise 76 in Section 1.3.1 and mentioned in Theorem 1.6, has a domain of all real numbers. As the domains of
, first introduced in Exercise 76 in Section 1.3.1 and mentioned in Theorem 1.6, has a domain of all real numbers. As the domains of  and
and  may not be all real numbers, we need the restrictions listed here. ↵
may not be all real numbers, we need the restrictions listed here. ↵ - In other words, invertible functions have exactly one inverse. ↵
- See Example 1.1.5 in Section 1.1 and Example 1.35 in Section 1.3.1. ↵
- i.e., no horizontal line intersects the graph more than once. ↵
- For example, if we know
 is one-to-one, we showed the graph of
is one-to-one, we showed the graph of  passes the HLT which, in turn, guarantees
passes the HLT which, in turn, guarantees  is invertible. ↵
is invertible. ↵ - Here, we use the Quadratic Formula to solve for
 . For `completeness,' we note you can (and should!) also consider solving for
. For `completeness,' we note you can (and should!) also consider solving for  by `completing' the square. ↵
by `completing' the square. ↵ - It is good review to actually do this! ↵
- Recall this means
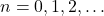 ↵
↵ - or, more precisely, appears to represent
 ↵
↵
Two functions are inverses if their compositions are both true for all x.
A function is invertible if the function has an inverse.
A function is one-to-one if whenever f(a)=f(b), then a=b.

