5.2 Properties and Graphs of Exponential Functions
Of all of the functions we study in this text, exponential functions are possibly the ones which impact everyday life the most. This section introduces us to these functions while the rest of the chapter will more thoroughly explore their properties.
Up to this point, we have dealt with functions which involve terms like ![]() ,
, ![]() , or
, or ![]() – in other words, terms of the form
– in other words, terms of the form ![]() where the base of the term,
where the base of the term, ![]() , varies but the exponent of each term,
, varies but the exponent of each term, ![]() , remains constant.
, remains constant.
In this chapter, we study functions of the form ![]() where the base
where the base ![]() is a constant and the exponent
is a constant and the exponent ![]() is the variable. We start our exploration of these functions with the time-honored classic,
is the variable. We start our exploration of these functions with the time-honored classic, ![]() .
.
We make a table of function values, plot enough points until we are more or less confident with the shape of the curve, and connect the dots in a pleasing fashion.

A few remarks about the graph of ![]() are in order. As
are in order. As ![]() and takes on values like
and takes on values like ![]() or
or ![]() , the function
, the function ![]() takes on values like
takes on values like ![]() or
or ![]()
In other words, as ![]() ,
, ![]()
That is, as ![]() ,
, ![]() . This produces the
. This produces the ![]() -axis,
-axis, ![]() as a horizontal asymptote to the graph as
as a horizontal asymptote to the graph as ![]()
On the flip side, as ![]() , we find
, we find ![]() ,
, ![]() , and so on, thus
, and so on, thus ![]()
We note that by `connecting the dots in a pleasing fashion,’ we are implicitly using the fact that ![]() is not only defined for all real numbers,[1] but is also continuous. Moreover, we are assuming
is not only defined for all real numbers,[1] but is also continuous. Moreover, we are assuming ![]() is increasing: that is, if
is increasing: that is, if ![]() , then
, then ![]() . While these facts are true, the proofs of these properties are best left to Calculus. For us, we assume these properties in order to state the domain of
. While these facts are true, the proofs of these properties are best left to Calculus. For us, we assume these properties in order to state the domain of ![]() is
is ![]() , the range of
, the range of ![]() is
is ![]() and,
and, ![]() is increasing, do
is increasing, do ![]() is one-to-one, hence invertible.
is one-to-one, hence invertible.
Suppose we wish to study the family of functions ![]() . Which bases
. Which bases ![]() make sense to study? We find that we run into difficulty if
make sense to study? We find that we run into difficulty if ![]() . For example, if
. For example, if ![]() , then the function
, then the function ![]() has trouble, for instance, at
has trouble, for instance, at ![]() because
because ![]() is not a real number. In general, if
is not a real number. In general, if ![]() is any rational number with an even denominator,[2] then
is any rational number with an even denominator,[2] then ![]() is not defined, so we must restrict our attention to bases
is not defined, so we must restrict our attention to bases ![]() .
.
What about ![]() ? The function
? The function ![]() is undefined for
is undefined for ![]() because we cannot divide by
because we cannot divide by ![]() and
and ![]() is an indeterminant form. For
is an indeterminant form. For ![]() ,
, ![]() so the function
so the function ![]() is the same as the function
is the same as the function ![]() ,
, ![]() . As we know everything about this function, we ignore this case.
. As we know everything about this function, we ignore this case.
The only other base we exclude is ![]() , because the function
, because the function ![]() for all real numbers
for all real numbers ![]() . We are now ready for our definition of exponential functions.
. We are now ready for our definition of exponential functions.
Definition 5.3
An exponential function is the function of the form
![]()
where ![]() is a real number,
is a real number, ![]() ,
, ![]() . The domain of an exponential function
. The domain of an exponential function ![]() .
.
NOTE: More specifically, ![]() is called the `base
is called the `base ![]() exponential function.’
exponential function.’
We leave it to the reader to verify[3] that if ![]() , then the exponential function
, then the exponential function ![]() will share the same basic shape and characteristics as
will share the same basic shape and characteristics as ![]()
What if ![]() ? Consider
? Consider ![]() . We could certainly build a table of values and connect the points, or we could take a step back and note that
. We could certainly build a table of values and connect the points, or we could take a step back and note that
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(x) & = & \left(\frac{1}{2}\right)^{x} \\ & = & \left(2^{-1}\right)^{x} \\ & = & 2^{-x} \\ & = & f(-x) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e93e97e47ddddb2f89b3217054bfec43_l3.png)
where ![]() . Per Section 1.6, the graph of
. Per Section 1.6, the graph of ![]() is obtained from the graph of
is obtained from the graph of ![]() by reflecting it across the
by reflecting it across the ![]() -axis.
-axis.

We see that the domain and range of ![]() match that of
match that of ![]() , namely
, namely ![]() and
and ![]() , respectively. Like
, respectively. Like ![]() ,
, ![]() is also one-to-one. Whereas
is also one-to-one. Whereas ![]() is always increasing,
is always increasing, ![]() is always decreasing. As a result, as
is always decreasing. As a result, as ![]() ,
, ![]() , and on the flip side, as
, and on the flip side, as ![]() ,
, ![]() . It shouldn’t be too surprising that for all choices of the base
. It shouldn’t be too surprising that for all choices of the base ![]() , the graph of
, the graph of ![]() behaves similarly to the graph of
behaves similarly to the graph of ![]()
We summarize the basic properties of exponential functions in the following theorem.
Theorem 5.3 Properties of Exponential Functions
Suppose ![]() .
.
- The domain of
 is
is  and the range of
and the range of  is
is 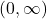 .
. 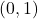 is on the graph of
is on the graph of  and
and 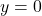 is a horizontal asymptote to the graph of
is a horizontal asymptote to the graph of  .
. is one-to-one, continuous and smooth[4]
is one-to-one, continuous and smooth[4]- If
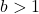 :
:
 is always increasing
is always increasing- As
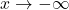 ,
, 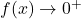
- As
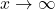 ,
, 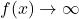
- The graph of
 resembles:
resembles:
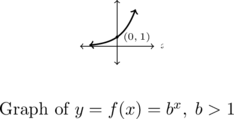
- If
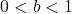 :
:
 is always decreasing
is always decreasing- As
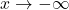 ,
, 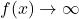
- As
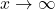 ,
, 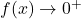
- The graph of
 resembles:
resembles:
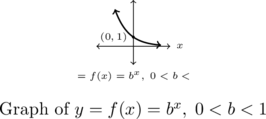
Exponential functions also inherit the basic properties of exponents from Theorem 4.3. We formalize these below and use them as needed in the coming examples.
Theorem 5.4 Algebraic Properties of Exponential Functions
Let ![]() be an exponential function (
be an exponential function (![]() ,
, ![]() ) and let
) and let ![]() and
and ![]() be real numbers.
be real numbers.
- Product Rule:
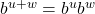
- Quotient Rule:
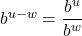
- Power Rule:
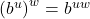
In addition to base ![]() which is important to computer scientists,[5] two other bases are used more often than not in scientific and economic circles. The first is base 10. Base 10 is called the `common base‘ and is important in the study of intensity (sound intensity, earthquake intensity, acidity, etc.)
which is important to computer scientists,[5] two other bases are used more often than not in scientific and economic circles. The first is base 10. Base 10 is called the `common base‘ and is important in the study of intensity (sound intensity, earthquake intensity, acidity, etc.)
The second base is an irrational number, ![]() . Like
. Like ![]() or
or ![]() , the decimal expansion of
, the decimal expansion of ![]() neither terminates nor repeats, so we represent this number by the letter `
neither terminates nor repeats, so we represent this number by the letter `![]() .’ A decimal approximation of
.’ A decimal approximation of ![]() is
is ![]() , so the function
, so the function ![]() is an increasing exponential function.
is an increasing exponential function.
The number ![]() is called the `natural base‘ for lots of reasons, one of which is that it `naturally’ arises in the study of growth functions in Calculus. We will more formally discuss the origins of
is called the `natural base‘ for lots of reasons, one of which is that it `naturally’ arises in the study of growth functions in Calculus. We will more formally discuss the origins of ![]() in Section 5.7.
in Section 5.7.
It is time for an example.
Example 5.2.1
Example 5.2.1.1a
Graph the following functions by starting with a basic exponential function and using transformations, Theorem 1.12. Track at least three points and the horizontal asymptote through the transformations.
![]()
Solution:
Graph ![]() .
.
The base of the exponent in ![]() is
is ![]() , so we start with the graph of
, so we start with the graph of ![]() .
.
To use Theorem 1.12, we first need to choose some `control points’ on the graph of ![]() . Because we are instructed to track three points (and the horizontal asymptote,
. Because we are instructed to track three points (and the horizontal asymptote, ![]() ) through the transformations, we choose the points corresponding to
) through the transformations, we choose the points corresponding to ![]() ,
, ![]() , and
, and ![]() :
: ![]() ,
, ![]() , and
, and ![]() , respectively.
, respectively.
Next, we need determine how to modify ![]() to obtain
to obtain ![]() . The key is to recognize the argument, or `inside’ of the function is the exponent and the `outside’ is anything outside the base of
. The key is to recognize the argument, or `inside’ of the function is the exponent and the `outside’ is anything outside the base of ![]() . Using these principles as a guide, we find
. Using these principles as a guide, we find ![]() .
.
Per Theorem 1.12, we first add ![]() to the
to the ![]() -coordinates of the points on the graph of
-coordinates of the points on the graph of ![]() , shifting the graph to the right
, shifting the graph to the right ![]() unit. Next, multiply the
unit. Next, multiply the ![]() -coordinates of each point on this new graph by
-coordinates of each point on this new graph by ![]() , vertically stretching the graph by a factor of
, vertically stretching the graph by a factor of ![]() .
.
Looking point by point, we have ![]() ,
, ![]() , and
, and ![]() .
.
The horizontal asymptote, ![]() remains unchanged under the horizontal shift and the vertical stretch because
remains unchanged under the horizontal shift and the vertical stretch because ![]() .
.
Below we graph ![]() on the left
on the left ![]() on the right.
on the right.
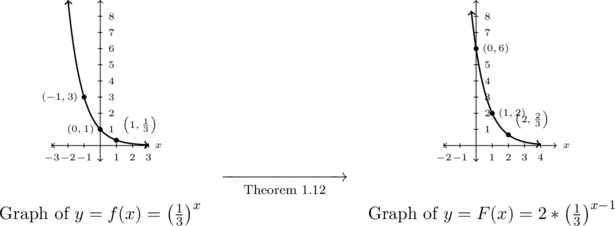
As always we can check our answer by verifying each of the points ![]() ,
, ![]() ,
, ![]() is on the graph of
is on the graph of ![]() by checking
by checking ![]() ,
, ![]() , and
, and ![]() .
.
We can check the end behavior as well, that is, as ![]() ,
, ![]() and as
and as ![]() ,
, ![]() . We leave these calculations to the reader.
. We leave these calculations to the reader.
Example 5.2.1.1b
Graph the following functions by starting with a basic exponential function and using transformations, Theorem 1.12. Track at least three points and the horizontal asymptote through the transformations.
![]()
Solution:
Graph ![]() .
.
The base of the exponential in ![]() is
is ![]() , so we start with the graph of
, so we start with the graph of ![]() .
.
Note that as ![]() is an irrational number, we will use the approximation
is an irrational number, we will use the approximation ![]() when plotting points. However, when it comes to tracking and labeling said points, we do so with exact coordinates, that is, in terms of
when plotting points. However, when it comes to tracking and labeling said points, we do so with exact coordinates, that is, in terms of ![]()
We choose points corresponding to ![]() ,
, ![]() , and
, and ![]() :
: ![]() ,
, ![]() , and
, and ![]() , respectively.
, respectively.
Next, we need to determine how the formula for ![]() can be obtained from the formula
can be obtained from the formula ![]() . Rewriting
. Rewriting ![]() , we find
, we find ![]()
Following Theorem 1.12, we first multiply the ![]() -coordinates of the graph of
-coordinates of the graph of ![]() by
by ![]() , effecting a reflection across the
, effecting a reflection across the ![]() -axis. Next, we multiply each of the
-axis. Next, we multiply each of the ![]() -coordinates by
-coordinates by ![]() which reflects the graph about the
which reflects the graph about the ![]() -axis. Finally, we add
-axis. Finally, we add ![]() to each of the
to each of the ![]() -coordinates of the graph from the second step which shifts the graph up
-coordinates of the graph from the second step which shifts the graph up ![]() units.
units.
Tracking points, we have ![]() ,
, ![]() , and
, and ![]()
The horizontal asymptote is unchanged by the reflections, but is shifted up ![]() units
units ![]()
We graph ![]() below on the left and the transformed function
below on the left and the transformed function ![]() below on the right. As usual, we can check our answer by verifying the indicated points do, in fact, lie on the graph of
below on the right. As usual, we can check our answer by verifying the indicated points do, in fact, lie on the graph of ![]() along with checking end behavior. We leave these details to the reader.
along with checking end behavior. We leave these details to the reader.
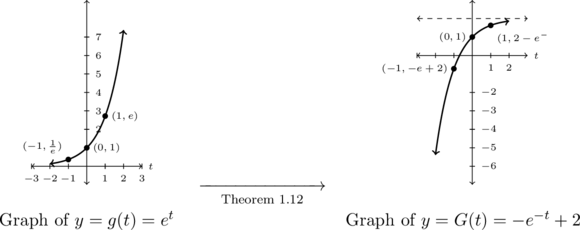
Example 5.2.1.2
Write a formula for the graph of the function below. Assume the base of the exponential is ![]() .
.
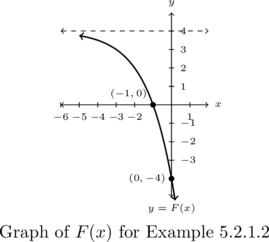
Solution:
Write a formula for the graph of the function above. Assume the base of the exponential is ![]() .
.
We are told to assume the base of the exponential function is ![]() , thus we assume the function
, thus we assume the function ![]() is the result of the transforming the graph of
is the result of the transforming the graph of ![]() using Theorem 1.12. This means we are tasked with finding values for
using Theorem 1.12. This means we are tasked with finding values for ![]() ,
, ![]() ,
, ![]() , and
, and ![]() so that
so that ![]()
Because the horizontal asymptote to the graph of ![]() is
is ![]() and the horizontal asymptote to the graph
and the horizontal asymptote to the graph ![]() is
is ![]() , we know the vertical shift is
, we know the vertical shift is ![]() units up, so
units up, so ![]() .
.
Next, looking at how the graph of ![]() approaches the vertical asymptote, it stands to reason the graph of
approaches the vertical asymptote, it stands to reason the graph of ![]() undergoes a reflection across
undergoes a reflection across ![]() -axis, meaning
-axis, meaning ![]() . For simplicity, we assume
. For simplicity, we assume ![]() and see if we can find values for
and see if we can find values for ![]() and
and ![]() that go along with this choice.
that go along with this choice.
Because ![]() and
and ![]() on the graph of
on the graph of ![]() , we know
, we know ![]() and
and ![]() . From
. From ![]() , we have
, we have ![]() or
or ![]() . Hence,
. Hence, ![]() is one solution.[6]
is one solution.[6]
Next, using ![]() , we get
, we get ![]() or
or ![]() . From this, we have
. From this, we have ![]() so
so ![]() . Putting this together with
. Putting this together with ![]() , we get
, we get ![]() so
so ![]() .
.
Hence, one solution to the problem is ![]() .
.
To check our answer, we leave it to the reader verify ![]() ,
, ![]() , as
, as ![]() ,
, ![]() and as
and as ![]() ,
, ![]() .
.
Because we made a simplifying assumption (![]() ), we may well wonder if our solution is the only solution. Indeed, we started with what amounts to three pieces of information and set out to determine the value of four constants. We leave this for a thoughtful discussion in Exercise 14.
), we may well wonder if our solution is the only solution. Indeed, we started with what amounts to three pieces of information and set out to determine the value of four constants. We leave this for a thoughtful discussion in Exercise 14.
Our next example showcases an important application of exponential functions: economic depreciation.
Example 5.2.2
Example 5.2.2.1
The value of a car can be modeled by ![]() , where
, where ![]() is number of years the car is owned and
is number of years the car is owned and ![]() is the value in thousands of dollars.
is the value in thousands of dollars.
Calculate and interpret ![]() ,
, ![]() , and
, and ![]() .
.
Solution:
Calculate and interpret ![]() ,
, ![]() , and
, and ![]() .
.
We find ![]() ,
, ![]() and
and ![]() .
.
![]() represents the number of years the car has been owned, so
represents the number of years the car has been owned, so ![]() corresponds to the purchase price of the car.
corresponds to the purchase price of the car. ![]() returns the value of the car in thousands of dollars, so
returns the value of the car in thousands of dollars, so ![]() means the car is worth 25,000 dollars when first purchased. Likewise,
means the car is worth 25,000 dollars when first purchased. Likewise, ![]() and
and ![]() means the car is worth 20, 000 dollars after one year of ownership and 16,000 dollars after two years, respectively.
means the car is worth 20, 000 dollars after one year of ownership and 16,000 dollars after two years, respectively.
Example 5.2.2.2
The value of a car can be modeled by ![]() , where
, where ![]() is number of years the car is owned and
is number of years the car is owned and ![]() is the value in thousands of dollars.
is the value in thousands of dollars.
Compute and interpret the average rate of change of ![]() over the intervals
over the intervals ![]() and
and ![]() and
and ![]() .
.
Solution:
Compute and interpret the average rate of change of ![]() over the intervals
over the intervals ![]() and
and ![]() and
and ![]() .
.
Recall to find the average rate of change of ![]() over an interval
over an interval ![]() , we compute:
, we compute: ![]() .
.
For the interval ![]() , we find
, we find
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \frac{V(1) - V(0)}{1-0} &=& \frac{20-25}{1} \\[6pt] &=& -5 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-2e244dfb3c1c0c36bd91d5347138b172_l3.png)
which means over the course of the first year of ownership, the value of the car depreciated, on average, at a rate of 5000 dollars per year.
For the interval ![]() , we compute
, we compute
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \frac{V(2) - V(0)}{2-0} &=& \frac{16-25}{2} \\[6pt] &=& -4.5 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b7ac48c18eecd1dd85ec00acad399df0_l3.png)
which means over the course of the first two years of ownership, the car lost, on average, 4500 dollars per year in value.
Finally, we find for the interval ![]() ,
,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \frac{V(2) - V(1)}{2-1} &=& \frac{16-20}{1} \\[6pt] &=& -4 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c954358ccdc8cce331aa9fadb2325c87_l3.png)
meaning the car lost, on average, 4000 dollars in value per year between the first and second years.
Notice that the car lost more value over the first year (5000 dollars) than it did the second year (4000 dollars), and these losses average out to the average yearly loss over the first two years (4500 dollars per year.)[7]
Example 5.2.2.3
The value of a car can be modeled by ![]() , where
, where ![]() is number of years the car is owned and
is number of years the car is owned and ![]() is the value in thousands of dollars.
is the value in thousands of dollars.
Determine and interpret ![]() ,
, ![]() and
and ![]() .
.
Solution:
Determine and interpret ![]() ,
, ![]() and
and ![]() .
.
We compute: ![]() ,
, ![]() , and
, and ![]() .
.
The ratio ![]() can be rewritten as
can be rewritten as ![]() which means that the value of the car after
which means that the value of the car after ![]() year,
year, ![]() is
is ![]() times, or
times, or ![]() the initial value of the car,
the initial value of the car, ![]() .
.
Similarly, the ratio ![]() rewritten as
rewritten as ![]() means the value of the car after 2 years,
means the value of the car after 2 years, ![]() is
is ![]() times, or
times, or ![]() the value of the car after one year,
the value of the car after one year, ![]() .
.
Finally, the ratio ![]() , or
, or ![]() means the value of the car after 2 years,
means the value of the car after 2 years, ![]() is
is ![]() times, or
times, or ![]() of the initial value of the car,
of the initial value of the car, ![]() .
.
Note that this last result tracks with the previous answers. Because ![]() and
and ![]() , we get
, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} V(2) &=& 0.8 V(1) \\ &=& 0.8 (0.8 V(0)) \\ &=& 0.64 V(0) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a25abfb5b0863615da239dca359af639_l3.png)
Also note it is no coincidence that the base of the exponential, ![]() has shown up in these calculations, as we’ll see in the next problem.
has shown up in these calculations, as we’ll see in the next problem.
Example 5.2.2.4
The value of a car can be modeled by ![]() , where
, where ![]() is number of years the car is owned and
is number of years the car is owned and ![]() is the value in thousands of dollars.
is the value in thousands of dollars.
For ![]() , find and interpret
, find and interpret ![]() and
and ![]() .
.
Solution:
For ![]() , find and interpret
, find and interpret ![]() and
and ![]() .
.
Using properties of exponents, we find
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \dfrac{V(t+1)}{V(t)} &=& \dfrac{25 (0.8)^{t+1}}{25 (0.8)^{t}} \\[6pt] &=& (0.8)^{t+1-t} \\ &=& 0.8 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4750e4779a4da50280c948cc4809b9bc_l3.png)
Rewriting, we have ![]() . This means after one year, the value of the car
. This means after one year, the value of the car ![]() is only
is only ![]() of the value it was a year ago,
of the value it was a year ago, ![]() .
.
Similarly, we find
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \dfrac{V(t+k)}{V(t)} &=& \dfrac{25 (0.8)^{t+k}}{25 (0.8)^{t}} \\[6pt] &=& (0.8)^{t+k-t} \\ &=& (0.8)^{k} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-ba07bd9808ba4c3f4d5d4d179cfb63a0_l3.png)
which, rewritten, says ![]() . This means in
. This means in ![]() years’ time, the value of the car
years’ time, the value of the car ![]() is only
is only ![]() times what it was worth
times what it was worth ![]() years ago,
years ago, ![]() .
.
These results shouldn’t be too surprising. Verbally, the function ![]() says to multiply
says to multiply ![]() by
by ![]() multiplied by itself
multiplied by itself ![]() times. Therefore, for each additional year, we are multiplying the value of the car by an additional factor of
times. Therefore, for each additional year, we are multiplying the value of the car by an additional factor of ![]() .
.
Example 5.2.2.5
The value of a car can be modeled by ![]() , where
, where ![]() is number of years the car is owned and
is number of years the car is owned and ![]() is the value in thousands of dollars.
is the value in thousands of dollars.
Compute and interpret ![]() ,
, ![]() , and
, and ![]() .
.
Solution:
Compute and interpret ![]() ,
, ![]() , and
, and ![]() .
.
We compute
![]()
![]()
and
![]()
The ratio ![]() computes the ratio of difference in the value of the car after the first year of ownership,
computes the ratio of difference in the value of the car after the first year of ownership, ![]() , to the initial value,
, to the initial value, ![]() . We find this to be
. We find this to be ![]() or a
or a ![]() decrease in value. This makes sense as we know from our answer to number 3, the value of the car after
decrease in value. This makes sense as we know from our answer to number 3, the value of the car after ![]() year,
year, ![]() is
is ![]() of the initial value,
of the initial value, ![]() . Indeed:
. Indeed:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \dfrac{V(1) - V(0)}{V(0)} & = & \dfrac{V(1)}{V(0)} - \dfrac{V(0)}{V(0)} \\[10pt] & = & \dfrac{V(1)}{V(0)} - 1 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-97aa47fa71de487ac8ad20a073760046_l3.png)
and because ![]() , we get
, we get
![]()
Likewise, the ratio ![]() means the value of the car has lost
means the value of the car has lost ![]() of its value over the course of the second year of ownership.
of its value over the course of the second year of ownership.
Finally, the ratio ![]() means that over the first two years of ownership, the car value has depreciated
means that over the first two years of ownership, the car value has depreciated ![]() of its initial purchase price. Again, this tracks with the result of number 3 which tells us that after two years, the car is only worth
of its initial purchase price. Again, this tracks with the result of number 3 which tells us that after two years, the car is only worth ![]() of its initial purchase price.
of its initial purchase price.
Example 5.2.2.6
The value of a car can be modeled by ![]() , where
, where ![]() is number of years the car is owned and
is number of years the car is owned and ![]() is the value in thousands of dollars.
is the value in thousands of dollars.
For ![]() , find and interpret
, find and interpret ![]() and
and ![]() .
.
Solution:
For ![]() , find and interpret
, find and interpret ![]() and
and ![]() .
.
Using properties of fractions and exponents, we get:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \dfrac{V(t+1) - V(t)}{V(t)} &=& \dfrac{25(0.8)^{t+1} - 25(0.8)^{t}}{25 (0.8)^{t}}\\[10pt] &=& \dfrac{25(0.8)^{t+1}}{25 (0.8)^{t}} - \dfrac{25 (0.8)^{t}}{25 (0.8)^{t}} \\[10pt] &=& 0.8 - 1 \\ &=& -0.2 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-ad91d49bba274641bd6bc2c9cb77c8c6_l3.png)
so after one year, the value of the car ![]() has lost
has lost ![]() of the value it was a year ago,
of the value it was a year ago, ![]() .
.
Similarly, we find:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \dfrac{V(t+k) - V(t)}{V(t)} &=& \dfrac{25(0.8)^{t+k} - 25(0.8)^{t}}{25 (0.8)^{t}} \\[10pt] &=& \dfrac{25(0.8)^{t+1}}{25 (0.8)^{t}} - \dfrac{25 (0.8)^{t}}{25 (0.8)^{t}} \\[10pt] &=& (0.8)^{k} - 1 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b5e78a2f59613e2a4263412511e7fb50_l3.png)
so after ![]() years’ time, the value of the car
years’ time, the value of the car ![]() has decreased by
has decreased by ![]() of the value
of the value ![]() years ago,
years ago, ![]() .
.
Example 5.2.2.7
The value of a car can be modeled by ![]() , where
, where ![]() is number of years the car is owned and
is number of years the car is owned and ![]() is the value in thousands of dollars.
is the value in thousands of dollars.
Graph ![]() starting with the graph of
starting with the graph of ![]() and using transformations.
and using transformations.
Solution:
Graph ![]() starting with the graph of
starting with the graph of ![]() and using transformations.
and using transformations.
To graph ![]() , we start with the basic exponential function
, we start with the basic exponential function ![]() .
.
The base ![]() satisfies
satisfies ![]() , therefore the graph of
, therefore the graph of ![]() is decreasing.
is decreasing.
We plot the ![]() -intercept
-intercept ![]() and two other points,
and two other points, ![]() and
and ![]() , and label the horizontal asymptote
, and label the horizontal asymptote ![]() .
.
To obtain the graph of ![]() , we multiply all of the
, we multiply all of the ![]() values in the graph by
values in the graph by ![]() (including the
(including the ![]() value of the horizontal asymptote) in accordance with Theorem 1.10 to obtain the points
value of the horizontal asymptote) in accordance with Theorem 1.10 to obtain the points ![]() ,
, ![]() and
and ![]() . The horizontal asymptote remains the same, (
. The horizontal asymptote remains the same, (![]() .) Finally, we restrict the domain to
.) Finally, we restrict the domain to ![]() to fit with the applied domain given to us.
to fit with the applied domain given to us.

Example 5.2.2.8
The value of a car can be modeled by ![]() , where
, where ![]() is number of years the car is owned and
is number of years the car is owned and ![]() is the value in thousands of dollars.
is the value in thousands of dollars.
Interpret the horizontal asymptote of the graph of ![]() .
.
Solution:
Interpret the horizontal asymptote of the graph of ![]() .
.
We see from the graph of ![]() that its horizontal asymptote is
that its horizontal asymptote is ![]() . This means as the car gets older, its value diminishes to
. This means as the car gets older, its value diminishes to ![]() .
.
Example 5.2.2.9
The value of a car can be modeled by ![]() , where
, where ![]() is number of years the car is owned and
is number of years the car is owned and ![]() is the value in thousands of dollars.
is the value in thousands of dollars.
Using technology and your graph, determine how long it takes for the car to depreciate to (a) one half its original value and (b) one quarter of its original value. Round your answers to the nearest hundredth.
Solution:
Using technology and your graph, determine how long it takes for the car to depreciate to (a) one half its original value and (b) one quarter of its original value. Round your answers to the nearest hundredth.
We know the value of the car, brand new, is 25,000 dollars so when we are asked to find when the car depreciates to one half and one quarter of this value, we are trying to find when the value of the car dips to 12,500 dollars and 6,125 dollars, respectively. ![]() is measured in thousands of dollars, so we this translates to solving the equations
is measured in thousands of dollars, so we this translates to solving the equations ![]() and
and ![]() .
.
Because we have yet to develop any analytic means to solve equations like ![]() (remember
(remember ![]() is in the exponent here), we are forced to approximate solutions to this equation numerically or use a graphing utility. Choosing the latter, we graph
is in the exponent here), we are forced to approximate solutions to this equation numerically or use a graphing utility. Choosing the latter, we graph ![]() along with the lines
along with the lines ![]() and
and ![]() and look for intersection points.
and look for intersection points.
We find ![]() and
and ![]() intersect at (approximately)
intersect at (approximately) ![]() which means the car depreciates to half its initial value in (approximately) 3.11 years. Similarly, we find the car depreciates to one-quarter its initial value after (approximately)
which means the car depreciates to half its initial value in (approximately) 3.11 years. Similarly, we find the car depreciates to one-quarter its initial value after (approximately) ![]() years.[8]
years.[8]
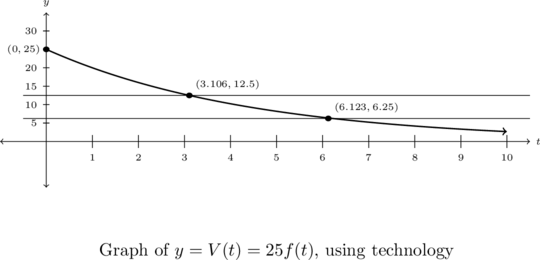
Some remarks about Example 5.2.2 are in order. First the function in the previous example is called a `decay curve’. Increasing exponential functions are used to model `growth curves’ and we shall see several different examples of those in Section 5.7.
Second, as seen in numbers 3 and 4, ![]() . That is to say, the function
. That is to say, the function ![]() has a constant unit multiplier, in this case,
has a constant unit multiplier, in this case, ![]() because to obtain the function value
because to obtain the function value ![]() , we multiply the function value
, we multiply the function value ![]() by
by ![]() . It is not coincidence that the multiplier here is the base of the exponential,
. It is not coincidence that the multiplier here is the base of the exponential, ![]() .
.
Indeed, exponential functions of the form ![]() have a constant unit multiplier,
have a constant unit multiplier, ![]() . To see this, note
. To see this, note
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \dfrac{f(x+1)}{f(x)} &=& \dfrac{a \cdot b^{x+1}}{ a \cdot b^{x}}\\[10pt] &=& b^{1} \\ &=& b \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d5f13581b2e9e88e846e4efc616d67f8_l3.png)
Hence ![]() . This will prove useful to us in Section 5.7 when making decisions about whether or not a data set represents exponential growth or decay.
. This will prove useful to us in Section 5.7 when making decisions about whether or not a data set represents exponential growth or decay.
We close this section with another important application of exponential functions, Newton’s Law of Cooling.
Example 5.2.3
Example 5.2.3.1
According to Newton’s Law of Cooling[9] the temperature of coffee ![]() (in degrees Fahrenheit)
(in degrees Fahrenheit) ![]() minutes after it is served can be modeled by
minutes after it is served can be modeled by ![]() .
.
Compute and interpret ![]() .
.
Solution:
Compute and interpret ![]() .
.
![]() , thus the temperature of the coffee when it is served is
, thus the temperature of the coffee when it is served is ![]() F.
F.
Example 5.2.3.2
According to Newton’s Law of Cooling[10] the temperature of coffee ![]() (in degrees Fahrenheit)
(in degrees Fahrenheit) ![]() minutes after it is served can be modeled by
minutes after it is served can be modeled by ![]() .
.
Sketch the graph of ![]() using transformations.
using transformations.
Solution:
Sketch the graph of ![]() using transformations.
using transformations.
To graph ![]() using transformations, we start with the basic function,
using transformations, we start with the basic function, ![]() . As in Example 5.2.1, we track the points
. As in Example 5.2.1, we track the points ![]() ,
, ![]() , and
, and ![]() , along with the horizontal asymptote
, along with the horizontal asymptote ![]() through each of transformations.
through each of transformations.
To use Theorem 1.12, we rewrite
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} T(t) &=& 70 + 90e^{-0.1t} \\ &=& 90e^{-0.1t}+70 \\ &=& 90 f(-0.1t)+70 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4f16e5eaa75a55ebf23a0ec4a0914a4a_l3.png)
Following Theorem 1.12, we first divide the ![]() -coordinates of each point on the graph of
-coordinates of each point on the graph of ![]() by
by ![]() which results in a horizontal expansion by a factor of
which results in a horizontal expansion by a factor of ![]() as well as a reflection about the
as well as a reflection about the ![]() -axis.
-axis.
Next, we multiply the ![]() -values of the points on this new graph by
-values of the points on this new graph by ![]() which effects a vertical stretch by a factor of
which effects a vertical stretch by a factor of ![]() . Last but not least, we add
. Last but not least, we add ![]() to all of the
to all of the ![]() -coordinates of the points on this second graph, which shifts the graph upwards
-coordinates of the points on this second graph, which shifts the graph upwards ![]() units.
units.
Tracking points, we have ![]() ,
, ![]() , and
, and ![]() . The horizontal asymptote
. The horizontal asymptote ![]() is unaffected by the horizontal expansion, reflection about the
is unaffected by the horizontal expansion, reflection about the ![]() -axis, and the vertical stretch, but the vertical shift moves the horizontal asymptote up
-axis, and the vertical stretch, but the vertical shift moves the horizontal asymptote up ![]() units,
units, ![]() . After restricting the domain to
. After restricting the domain to ![]() , we get the graph on the right.
, we get the graph on the right.
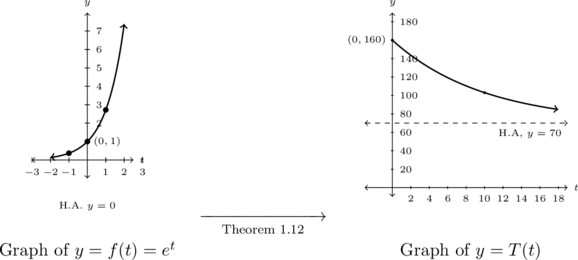
Example 5.2.3.3
According to Newton’s Law of Cooling[11] the temperature of coffee ![]() (in degrees Fahrenheit)
(in degrees Fahrenheit) ![]() minutes after it is served can be modeled by
minutes after it is served can be modeled by ![]() .
.
Determine and interpret the behavior of ![]() as
as ![]() .
.
Solution:
Determine and interpret the behavior of ![]() as
as ![]() .
.
We can determine the behavior of ![]() as
as ![]() two ways. First, we can employ the `number sense’ developed in Chapter 3.
two ways. First, we can employ the `number sense’ developed in Chapter 3.
That is, as ![]() , we get
, we get ![]() . As
. As ![]() ,
, ![]() . The larger
. The larger ![]() becomes, the smaller
becomes, the smaller ![]() becomes, so the term
becomes, so the term ![]() .
.
Hence, ![]() .
.
Alternatively, we can look to the graph of ![]() . We know the horizontal asymptote is
. We know the horizontal asymptote is ![]() which means as
which means as ![]() ,
, ![]() .
.
In either case, we find that as time goes by, the temperature of the coffee is cooling to ![]() Fahrenheit, ostensibly room temperature.
Fahrenheit, ostensibly room temperature.
5.2.1 Section Exercises
In Exercises 1 – 8, sketch the graph of ![]() by starting with the graph of
by starting with the graph of ![]() and using transformations. Track at least three points of your choice and the horizontal asymptote through the transformations. State the domain and range of
and using transformations. Track at least three points of your choice and the horizontal asymptote through the transformations. State the domain and range of ![]() .
.
 and
and 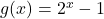
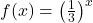 and
and 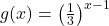
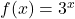 and
and 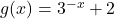
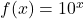 and
and 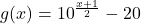
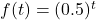 and
and 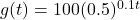
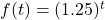 and
and 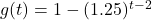
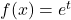 and
and 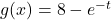
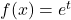 and
and 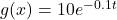
In Exercises, 9 – 12, the graph of an exponential function is given. Find a formula for the function in the form ![]() .
.
- Points:
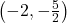 ,
, 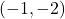 ,
, 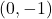 , Asymptote:
, Asymptote: 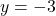
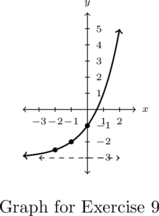
- Points:
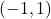 ,
, 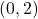 ,
, 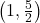 , Asymptote:
, Asymptote: 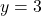
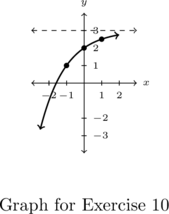
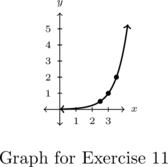
- Points:
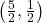 ,
, 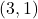 ,
, 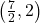 , Asymptote:
, Asymptote: 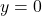
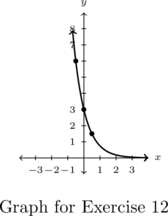
- Points:
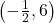 ,
, 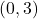 ,
, 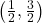 , Asymptote:
, Asymptote: 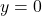
- Find a formula for each graph in Exercises 9 – 12 of the form
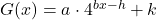 . Did you change your solution methodology? What is the relationship between your answers for
. Did you change your solution methodology? What is the relationship between your answers for 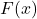 and
and 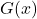 for each graph?
for each graph? - In Example 5.2.1 number 2, we obtained the solution
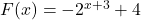 as one formula for the given graph by making a simplifying assumption that
as one formula for the given graph by making a simplifying assumption that 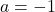 . This exercises explores if there are any other solutions for different choices of
. This exercises explores if there are any other solutions for different choices of  .
.
- Show
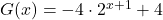 also fits the data for the given graph, and use properties of exponents to show
also fits the data for the given graph, and use properties of exponents to show 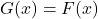 . (Use the fact that
. (Use the fact that 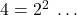 )
) - With help from your classmates, find solutions to Example 5.2.1 number 2 using
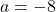 ,
, 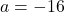 and
and 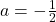 . Show all your solutions can be rewritten as:
. Show all your solutions can be rewritten as: 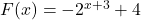 .
. - Using properties of exponents and the fact that the range of
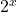 is
is 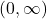 , show that any function of the form
, show that any function of the form 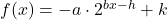 for
for 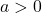 can be rewritten as
can be rewritten as 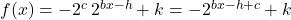 . Relabeling, this means every function of the form
. Relabeling, this means every function of the form 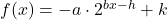 with four parameters (
with four parameters ( ,
,  ,
,  , and
, and 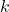 ) can be rewritten as
) can be rewritten as 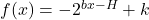 , a formula with just three parameters:
, a formula with just three parameters:  ,
, 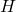 , and
, and 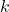 . Conclude that every solution to Example 5.2.1 number 2 reduces to
. Conclude that every solution to Example 5.2.1 number 2 reduces to 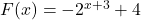 .
.
- Show
In Exercises 15 – 20, write the given function as a nontrivial decomposition of functions as directed.
- For
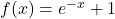 , find functions
, find functions  and
and  so that
so that 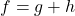
- For
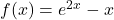 , find functions
, find functions  and
and  so that
so that 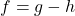
- For
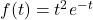 , find functions
, find functions  and
and  so that
so that 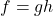
- For
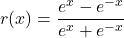 , find functions
, find functions  and
and  so
so 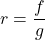
- For
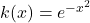 , find functions
, find functions  and
and  so that
so that 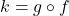
- For
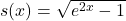 , find functions
, find functions  and
and  so
so 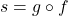
- Show that the average rate of change of a function over the interval
![Rendered by QuickLaTeX.com [x, x+2]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7db3a735c631b1ff6b2b05612550d08c_l3.png) is average of the average rates of change of the function over the intervals
is average of the average rates of change of the function over the intervals ![Rendered by QuickLaTeX.com [x,x+1]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4a70436c2270fec5d9ea28f7a9705643_l3.png) and
and ![Rendered by QuickLaTeX.com [x+1, x+2]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-1016e47300c03583d3f5f5b1880c421d_l3.png) . Can the same be said for the average rate of change of the function over
. Can the same be said for the average rate of change of the function over ![Rendered by QuickLaTeX.com [x, x+3]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-dba1c83cb82b760ed4a3b67c9af1385f_l3.png) and the average of the average rates of change over
and the average of the average rates of change over ![Rendered by QuickLaTeX.com [x, x+1]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4eafa73e90e265f59fddff342ca0d621_l3.png) ,
, ![Rendered by QuickLaTeX.com [x+1, x+2]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-1016e47300c03583d3f5f5b1880c421d_l3.png) , and
, and ![Rendered by QuickLaTeX.com [x+2, x+3]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-adcae0e9a758c305fb1731646de64516_l3.png) ? Generalize.
? Generalize. - Which is larger:
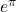 or
or 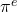 ? How do you know? Can you find a proof that doesn’t use technology?
? How do you know? Can you find a proof that doesn’t use technology?
Section 5.2 Exercise Answers can be found in the Appendix … Coming soon
- See the discussion of real number exponents in Section 4.2. ↵
- or, as we defined real number exponents in Section 4.2, if
 is an irrational number
is an irrational number  ↵
↵ - Meaning, graph some more examples on your own. ↵
- Recall that this means the graph of
 has no sharp turns or corners. ↵
has no sharp turns or corners. ↵ - The digital world is comprised of bytes which take on one of two values: 0 or `off' and 1 or `on.' ↵
- This is the only solution.
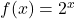 , so the equation
, so the equation 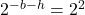 is equivalent to the functional equation
is equivalent to the functional equation 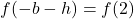 .
.  is one-to-one, so we know this is true only when
is one-to-one, so we know this is true only when 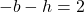 . ↵
. ↵ - It turns out for any function
 , the average rate of change over the interval
, the average rate of change over the interval ![Rendered by QuickLaTeX.com [x, x+2]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7db3a735c631b1ff6b2b05612550d08c_l3.png) is the average of the average rates of change of
is the average of the average rates of change of  over
over ![Rendered by QuickLaTeX.com [x, x+1]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4eafa73e90e265f59fddff342ca0d621_l3.png) and
and ![Rendered by QuickLaTeX.com [x+1, x+2]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-1016e47300c03583d3f5f5b1880c421d_l3.png) . See Exercise 21. ↵
. See Exercise 21. ↵ - It turns out that it takes exactly twice as long for the car to depreciate to one-quarter of its initial value as it takes to depreciate to half its initial value. Can you see why? ↵
- We will discuss this in greater detail in Section 5.7. ↵
- We will discuss this in greater detail in Section 5.7. ↵
- We will discuss this in greater detail in Section 5.7. ↵
A function of the form b raised to the x, where b is a positive real number, not equal to zero, and x is any real number.

