Appendix 1: Homework Answers for Chapter 0
Section 0.5 Answers
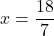
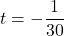
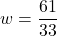
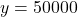
- All real numbers
- No solution
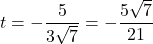
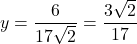
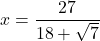
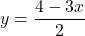 or
or 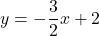
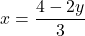 or
or 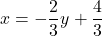
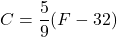 or
or 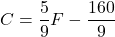
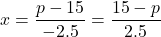 or
or 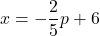
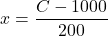 or
or 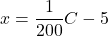
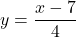 or
or 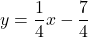
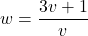 , provided
, provided 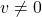
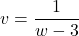 , provided
, provided 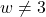
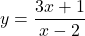 , provided
, provided 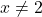
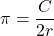 , provided
, provided 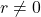
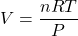 , provided
, provided 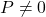
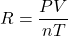 , provided
, provided 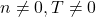
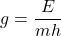 , provided
, provided 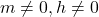
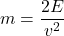 , provided
, provided 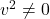 (so
(so 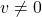 )
)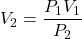 , provided
, provided 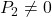
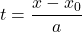 , provided
, provided 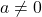
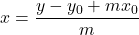 or
or 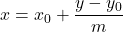 , provided
, provided 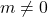
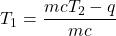 or
or 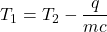 , provided
, provided 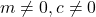
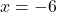 or
or 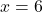
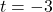 or
or 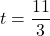
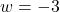 or
or 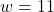
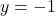 or
or 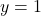
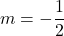 or
or 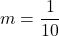
- No solution
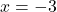 or
or 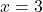
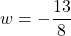 or
or 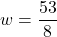
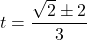
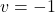 or
or 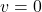
- No solution
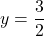
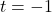 or
or 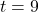
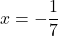 or
or 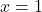
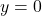 or
or 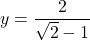
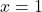
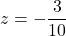
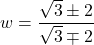 See footnote[1]
See footnote[1]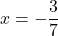 or
or 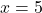
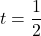 or
or 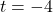
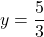 or
or 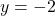
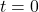 or
or 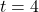
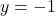 or
or 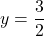
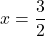 or
or 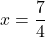
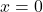 or
or 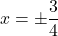
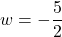 or
or 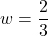
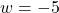 or
or 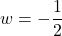
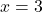 or
or 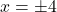
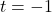 ,
, 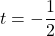 , or
, or 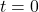
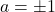
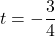 or
or 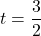
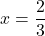
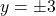
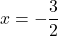

![Rendered by QuickLaTeX.com t = -\dfrac{\sqrt[3]{3}}{2}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-645ac3c7e502d5482bec1f98061e7800_l3.png)
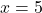
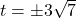
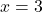
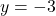
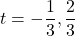
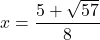
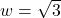
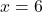
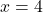
![Rendered by QuickLaTeX.com h = \sqrt[3]{\dfrac{12I}{b}}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9aa85ac35792e8f1470aec2f9248b12e_l3.png)
![Rendered by QuickLaTeX.com a = \dfrac{2 \sqrt[4]{I_{0}}}{\sqrt[4]{5\sqrt{3}}}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c52feae6953d7f9187d2913c465fb1cf_l3.png)
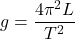
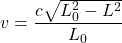
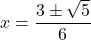
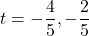
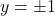 ,
, 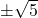
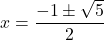
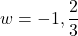
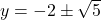
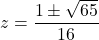

- No real solution
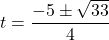
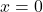
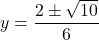
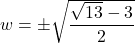
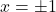 \
\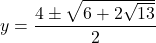
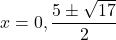
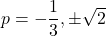
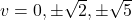
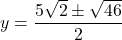
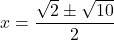
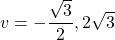
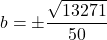
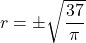
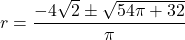
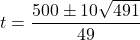
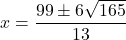
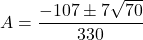
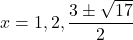
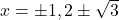
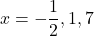
- The discriminant is:
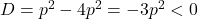 . because
. because 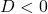 , there are no real solutions.
, there are no real solutions. 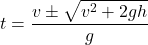
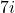
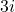
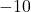
- 10
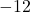
- 12
- 3
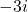
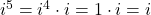
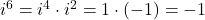
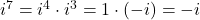
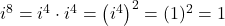
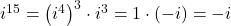
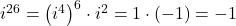
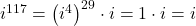
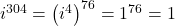
- For
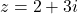 and
and 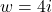
- For
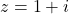 and
and 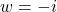
- For
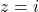 and
and 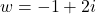
- For
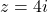 and
and 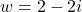
- For
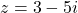 and
and 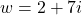
- For
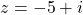 and
and 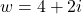
- For
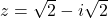 and
and 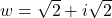
- For
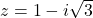 and
and 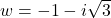
- For
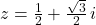 and
and 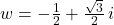
- For
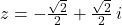 and
and 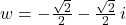
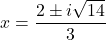
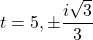
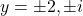
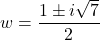
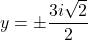
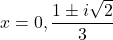
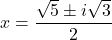
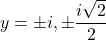
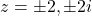
- That is,
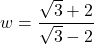 or
or 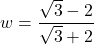 ↵
↵