0.3 Factoring Expressions

Vanessa Coffelt

0.3 Factoring Expressions

Now that we have reviewed the basics of polynomial arithmetic it’s time to review the basic techniques of factoring polynomial expressions. Our goal is to apply these techniques to help us solve certain specialized classes of non-linear equations. Given that `factoring’ literally means to resolve a product into its factors, it is, in the purest sense, `undoing’ multiplication. If this sounds like division to you then you’ve been paying attention. Let’s start with a numerical example.

Suppose we are asked to factor $16337$ . We could write $16337 = 16337 \cdot 1$ , and while this is technically a factorization of $16337$ , it’s probably not an answer the poser of the question would accept. Usually, when we’re asked to factor a natural number, we are being asked to resolve it into to a product of so-called `prime’ numbers.^[1] Recall that prime numbers are defined as natural numbers whose only (natural number) factors are themselves and $1$ . They are, in essence, the `building blocks’ of natural numbers as far as multiplication is concerned. Said differently, we can build – via multiplication – any natural number given enough primes.

So how do we find the prime factors of $16337$ ? We start by dividing each of the primes: $2$ , $3$ , $5$ , $7$ , etc., into $16337$ until we get a remainder of $0$ . Eventually, we determine that $16337 \div 17 = 961$ with a remainder of $0$ , which means $16337 = 17 \cdot 961$ . So factoring and division are indeed closely related – factors of a number are precisely the divisors of that number which produce a zero remainder.^[2] We continue our efforts to see if $961$ can be factored down further, and we find that $961 = 31 \cdot 31$ . Hence, $16337$ can be `completely factored’ as $17 \cdot 31^2$ . (This factorization is called the prime factorization of $16337$ .)

In factoring natural numbers, our building blocks are prime numbers, so to be completely factored means that every number used in the factorization of a given number is prime. One of the challenges when it comes to factoring polynomial expressions is to explain what it means to be `completely factored’. In this section, our `building blocks’ for factoring polynomials are `irreducible’ polynomials as defined below.

Definition 0.4

A polynomial is said to be irreducible if it cannot be written as the product of polynomials of lower degree.

While Definition 0.4 seems straightforward enough, sometimes a greater level of specificity is required. For example, $x^2 - 3 = (x-\sqrt{3})(x + \sqrt{3})$ . While $x-\sqrt{3}$ and $x+\sqrt{3}$ are perfectly fine polynomials, factoring which requires irrational numbers is usually saved for a more advanced treatment of factoring. For now, we will restrict ourselves to factoring using rational coefficients. So, while the polynomial $x^2 - 3$ can be factored using irrational numbers, it is called irreducible over the rationals, because there are no polynomials with rational coefficients of smaller degree which can be used to factor it.^[3]

Due to the fact that polynomials involve terms, the first step in any factoring strategy involves pulling out factors which are common to all of the terms. For example, in the polynomial $18x^2y^3 - 54x^3y^2 - 12xy^2$ , each coefficient is a multiple of $6$ so we can begin the factorization as $6(3x^2y^3 - 9x^3y^2 - 2xy^2)$ . The remaining coefficients: $3$ , $9$ and $2$ , have no common factors so $6$ was the greatest common factor. What about the variables? Each term contains an $x$ , so we can factor an $x$ from each term. When we do this, we are effectively dividing each term by $x$ which means the exponent on $x$ in each term is reduced by $1$ : $6x(3xy^3 - 9x^2y^2 - 2y^2)$ . Next, we see that each term has a factor of $y$ in it. In fact, each term has at least two factors of $y$ in it, as the lowest exponent on $y$ in each term is $2$ . This means that we can factor $y^2$ from each term. Again, factoring out $y^2$ from each term is tantamount to dividing each term by $y^2$ so the exponent on $y$ in each term is reduced by two: $6xy^2(3xy - 9x^2 - 2)$ . Just like we checked our division by multiplication in the previous section, we can check our factoring here by multiplication, too.

$\begin{array}{rcl}6xy^2(3xy - 9x^2 - 2) &=& (6xy^2)(3xy) - (6xy^2)(9x^2) - (6xy^2)(2) \\ &=& 18x^2y^3 - 54x^3y^2 - 12xy^2 \, \checkmark. \end{array}$

We summarize how to determine the Greatest Common Factor (G.C.F.) of a polynomial expression below.

Determining the G.C.F. of a Polynomial Expression

If the coefficients are integers, identify the G.C.F. of the coefficients.
Note 1: If all of the coefficients are negative, consider the negative as part of the G.C.F..
Note 2: If the coefficients involve fractions, get a common denominator, combine numerators, reduce to lowest terms and apply this step to the polynomial in the numerator.
If a variable is common to all of the terms, the G.C.F. contains that variable to the smallest exponent which appears among the terms.

For example, to factor $-\frac{3}{5}z^3 - 6z^2$ , we would first get a common denominator and factor as:

$\begin{array}{rcl} -\frac{3}{5}z^3 - 6z^2 &=& \frac{-3z^3 - 30z^2}{5} \\[5pt] &=& \frac{-3z^2(z + 10)}{5} \\[5pt] &=& -\frac{3z^2(z + 10)}{5} \\[5pt] &=& -\frac{3}{5}z^{2}(z + 10) \end{array}$

We now list some common factoring formulas, each of which can be verified by multiplying out the right side of the equation. While they all should look familiar – this is a review section after all – some should look more familiar than others because they are `special product’ formulas.

Common Factoring Formulas

Perfect Square Trinomials: 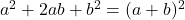$a^2 + 2ab + b^2 = (a+b)^2$ and $a^2 - 2ab + b^2 = (a-b)^2$
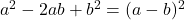
Difference of Two Squares: $a^2 - b^2 = (a-b)(a+b)$
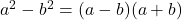
Note: In general, the sum of squares,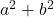 $a^2 + b^2$ is irreducible over the rationals.
Sum of Two Cubes: $a^3 + b^3 = (a + b)(a^2 - ab + b^2)$
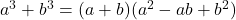
Note: In general,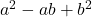 $a^2 - ab + b^2$ is irreducible over the rationals.
Difference of Two Cubes: $a^3 - b^3 = (a - b)(a^2 + ab + b^2)$
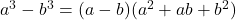
Note: In general,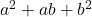 $a^2 + ab + b^2$ is irreducible over the rationals.

The example on the next page gives us practice with these formulas.

Example 0.3.1

Example 0.3.1.1

Factor the following polynomials completely over the rationals. That is, write each polynomial as a product polynomials of lowest degree which are irreducible over the rationals.

$18x^2 - 48x + 32$

Solution:

Factor $18x^2 - 48x + 32$ .

Our first step is to factor out the G.C.F. which in this case is $2$ . To match what is left with one of the special forms, we rewrite $9x^2 = (3x)^2$ and $16 = 4^2$ . We see that we have a perfect square trinomial, because the `middle’ term is $-24x = -2(4)(3x)$ .

$\begin{array}{rclr} 18x^2 - 48x + 32 & = & 2(9x^2 - 24x + 16) & \text{Factor out G.C.F.}\\ & = & 2((3x)^2 - 2(4)(3x) + (4)^2) & \\ & = & 2(3x-4)^2 & \text{Perfect Square Trinomial: $a = 3x$, $b=4$} \\ \end{array}$

Our final answer is $2(3x-4)^2$ .

To check our work, we multiply out $2(3x-4)^2$ to show that it equals $18x^2 - 48x + 32$ .

Example 0.3.1.2

Factor the following polynomials completely over the rationals. That is, write each polynomial as a product polynomials of lowest degree which are irreducible over the rationals.

$64y^2 - 1$

Solution:

Factor $64y^2 - 1$ .

For $64y^2 - 1$ , we note that the G.C.F. of the terms is just $1$ , so there is nothing (of substance) to factor out of both terms.

Due to the fact that $64y^2 - 1$ is the difference of two terms, one of which is a square, we look to the Difference of Squares Formula for inspiration. Seeing $64y^2 = (8y)^2$ and $1 = 1^2$ , we get

$\begin{array}{rclr} 64y^2 - 1 & = & (8y)^2 - 1^2 & \\ & = & (8y-1)(8y+1) & \text{Difference of Squares, $a = 8y$, $b = 1$} \end{array}$

As before, we can check our final answer by multiplying out $(8y-1)(8y+1)$ to show that it equals $64y^2 - 1$ .

Example 0.3.1.3

Factor the following polynomials completely over the rationals. That is, write each polynomial as a product polynomials of lowest degree which are irreducible over the rationals.

$75t^4 + 30t^3 + 3t^2$

Solution:

Factor $75t^4 + 30t^3 + 3t^2$ .

The G.C.F. of the terms in $75t^4 + 30t^3 + 3t^2$ is $3t^2$ , so we factor that out first.

$\begin{array}{rclr} 75t^4 + 30t^3 + 3t^2 & = & 3t^2 (25t^2+10t + 1) & \text{Factor out G.C.F.}\\ \end{array}$

We identify what remains as a perfect square trinomial:

$\begin{array}{rclr} 3t^2 (25t^2+10t + 1)& = & 3t^2 ((5t)^2 + 2(1)(5t) + 1^2) & \\ & = & 3t^2 (5t+1)^2 & \text{Perfect Square Trinomial, $a = 5t$, $b = 1$} \\ \end{array}$

Our final answer is $3t^2 (5t+1)^2$ , which the reader is invited to check.

Example 0.3.1.4

Factor the following polynomials completely over the rationals. That is, write each polynomial as a product polynomials of lowest degree which are irreducible over the rationals.

$w^4 z - w z^4$

Solution:

Factor $w^4 z - w z^4$ .

For $w^4 z - w z^4$ , we identify the G.C.F. as $wz$ and once we factor it out a difference of cubes is revealed:

$\begin{array}{rclr} w^4 z - w z^4 & = & wz(w^3 - z^3) & \text{Factor out G.C.F.} \\ & = & wz(w-z)(w^2+wz+z^2) & \text{Difference of Cubes, $a=w$, $b = z$} \\ \end{array}$

Our final answer is $wz(w-z)(w^2+wz+z^2)$ .

The reader is strongly encouraged to multiply this out to see that it reduces to $w^4 z - w z^4$ .

Example 0.3.1.5

Factor the following polynomials completely over the rationals. That is, write each polynomial as a product polynomials of lowest degree which are irreducible over the rationals.

$81 - 16t^4$

Solution:

Factor $81 - 16t^4$ .

The G.C.F. of the terms in $81 - 16t^4$ is just $1$ so there is nothing of substance to factor out from both terms.

With just a difference of two terms, we are limited to fitting this polynomial into either the Difference of Two Squares or Difference of Two Cubes formula. With the variable here being $t^4$ , and $4$ is a multiple of $2$ , we can think of $t^4 = (t^2)^2$ . This means that we can write $16t^4 = (4t^2)^2$ which is a perfect square. (As $4$ is not a multiple of $3$ , we cannot write $t^4$ as a perfect cube of a polynomial.) Identifying $81 = 9^2$ and $16t^4 = (4t^2)^2$ , we apply the Difference of Squares Formula to get:

$\begin{array}{rclr} 81 - 16t^4 & = & 9^2 - (4t^2)^2 & \\ & = & (9-4t^2)(9+4t^2) & \text{Difference of Squares, $a = 9$, $b = 4t^2$} \\ \end{array}$

At this point, we have an opportunity to proceed further in the first quantity. Identifying $9 = 3^2$ and $4t^2 = (2t)^2$ , we see that we have another difference of squares in the first quantity, which we can reduce. (The sum of two squares in the second quantity cannot be factored over the rationals.)

$\begin{array}{rclr} 81 - 16t^4 & = & (9-4t^2)(9+4t^2) & \\ & = & (3^2 - (2t)^2) (9 + 4t^2) & \\ & = & (3 - 2t)(3+2t)(9 + 4t^2) & \text{Difference of Squares, $a = 3$, $b = 2t$} \\ \end{array}$

As always, the reader is encouraged to multiply out $(3 - 2t)(3+2t)(9 + 4t^2)$ to check the result.

Example 0.3.1.6

Factor the following polynomials completely over the rationals. That is, write each polynomial as a product polynomials of lowest degree which are irreducible over the rationals.

$x^6 - 64$

Solution:

Factor $x^6 - 64$ .

With a G.C.F. of $1$ and just two terms, $x^6 - 64$ is a candidate for both the Difference of Squares and the Difference of Cubes formulas. Notice that we can identify $x^6 = (x^3)^2$ and $64 = 8^2$ (both perfect squares), but also $x^6 = (x^2)^3$ and $64 = 4^3$ (both perfect cubes). If we follow the Difference of Squares approach, we get:

$\begin{array}{rclr} x^6 - 64 & = & (x^3)^2 - 8^2 & \\ & = & (x^3 - 8)(x^3 + 8) & \text{Difference of Squares, $a = x^3$ and $b = 8$} \\ \end{array}$

At this point, we have an opportunity to use both the Difference and Sum of Cubes formulas:

$\begin{array}{rclr} x^6 - 64 & = & (x^3 - 2^3)(x^3 + 2^3) & \\ & = & (x-2)(x^2+2x+2^2)(x+2)(x^2 - 2x + 2^2) & \text{Sum / Diff. of Cubes, $a = x$, $b = 2$} \\ & = & (x-2)(x+2)(x^2-2x+4)(x^2+2x+4) & \text{Rearrange factors} \\ \end{array}$

From this approach, our final answer is $(x-2)(x+2)(x^2-2x+4)(x^2+2x+4)$ .

Following the Difference of Cubes Formula approach, we get:

$\begin{array}{rclr} x^6 - 64 & = & (x^2)^3 - 4^3 & \\ & = & (x^2 - 4)((x^2)^2 + 4x^2 + 4^2) & \text{Difference of Cubes, $a = x^2$, $b = 4$} \\ & = & (x^2 - 4)(x^4 + 4x^2 + 16) & \\ \end{array}$

At this point, we recognize $x^2 - 4$ as a difference of two squares:

$\begin{array}{rclr} x^6 - 64 & = & (x^2 - 2^2)(x^4 + 4x^2 + 16) & \\ & = & (x-2)(x+2)(x^4 + 4x^2 + 16) & \text{Difference of Squares, $a = x$, $b = 2$} \\ \end{array}$

Unfortunately, the remaining factor $x^4 + 4x^2 + 16$ is not a perfect square trinomial – the middle term would have to be $8x^2$ for this to work – so our final answer using this approach is $(x-2)(x+2)(x^4 + 4x^2 + 16)$ .

This isn’t as factored as our result from the Difference of Squares approach which was $(x-2)(x+2)(x^2-2x+4)(x^2+2x+4)$ . While it is true that $x^4 + 4x^2 + 16 =$ $(x^2-2x+4)(x^2+2x+4)$ , there is no `intuitive’ way to motivate this factorization at this point.^[4]

The moral of the story? When given the option between using the Difference of Squares and Difference of Cubes, start with the Difference of Squares.

Our final answer to this problem is $(x-2)(x+2)(x^2-2x+4)(x^2+2x+4)$ .

The reader is strongly encouraged to show that this reduces down to $x^6 - 64$ after performing all of the multiplication.

The formulas above, while useful, can only take us so far. Thus, we need to review some additional factoring strategies which should be good friends from back in the day!

Additional Factoring Formulas

`un-F.O.I.L.ing’: Given a trinomial 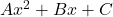$Ax^2 + Bx + C$ , try to reverse the F.O.I.L. process.
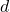That is, find $a$ , $b$ , $c$ and $d$ such that $Ax^2 + Bx + C= (ax+b)(cx+d)$ .
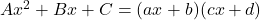Note: This means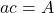 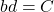$ac = A$ , $bd = C$ and $B = ad+bc$ .
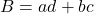Factor by Grouping: If the expression contains four terms with no common factors among the four terms, try `factor by grouping’:
$ac + bc + ad + bd = (a +b)c + (a+b)d = (a+b)(c+d)$

The techniques of `un-F.O.I.L.ing’ and `factoring by grouping’ are difficult to describe in general but should make sense to you with enough practice. Be forewarned – like all `Rules of Thumb’, these strategies work just often enough to be useful, but you can be sure there are exceptions which will defy any advice given here and will require some `inspiration’ to solve. Even though Chapter 2 will give us more powerful factoring methods, we’ll find that, in the end, there is no single algorithm for factoring which works for every polynomial. In other words, there will be times when you just have to try something and see what happens.

Example 0.3.2

Example 0.3.2.1

Factor the following polynomials completely over the integers. This means that all of the coefficients in the factors will be integers. While it was decided to avoid fractions in this set of examples, don’t get complacent, though, because fractions will return with a vengeance soon enough.

$x^2 - x - 6$

Solution:

Factor $x^2 - x - 6$ .

The G.C.F. of the terms $x^2 - x - 6$ is $1$ and $x^2 - x - 6$ isn’t a perfect square trinomial (Think about why not.) so we try to reverse the F.O.I.L. process and look for integers $a$ , $b$ , $c$ and $d$ such that $(ax + b)(cx + d) = x^2 - x - 6$ .

To get started, we note that $ac = 1$ . Because $a$ and $c$ are meant to be integers, that leaves us with either $a$ and $c$ both being $1$ , or $a$ and $c$ both being $-1$ . We’ll go with $a = c = 1$ , as we can factor the negatives into our choices for $b$ and $d$ . This yields $(x+b)(x+d) = x^2-x-6$ .

Next, we use the fact that $bd = -6$ . The product is negative so we know that one of $b$ or $d$ is positive and the other is negative. Given $b$ and $d$ are integers, one of $b$ or $d$ is $\pm 1$ and the other is $\mp 6$ OR one of $b$ or $d$ is $\pm 2$ and the other is $\mp 3$ .

After some guessing and checking, we find that $x^2 - x - 6 = (x+2)(x-3)$ .

Example 0.3.2.2

Factor the following polynomials completely over the integers. This means that all of the coefficients in the factors will be integers. While it was decided to avoid fractions in this set of examples, don’t get complacent, though, because fractions will return with a vengeance soon enough.

$2t^2 - 11t + 5$

Solution:

Factor $2t^2 - 11t + 5$ .

As with the previous example, we check the G.C.F. of the terms in $2t^2 - 11t + 5$ , determine it to be $1$ and see that the polynomial doesn’t fit the pattern for a perfect square trinomial.

We now try to find integers $a$ , $b$ , $c$ and $d$ such that $(at+b)(ct+d) = 2t^2 - 11t + 5$ . As $ac = 2$ , we have that one of $a$ or $c$ is $2$ , and the other is $1$ . (Once again, we ignore the negative options.) At this stage, there is nothing really distinguishing $a$ from $c$ so we choose $a = 2$ and $c = 1$ .

Now we look for $b$ and $d$ such that $(2t + b)(t+d) = 2t^2 - 11t + 5$ . We know $bd = 5$ so one of $b$ or $d$ is $\pm 1$ and the other $\pm 5$ . Given that $bd$ is positive, $b$ and $d$ must have the same sign. The negative middle term $-11t$ guides us to guess $b = -1$ and $d = -5$ so that we get $(2t -1)(t -5) = 2t^2 - 11t + 5$ . We verify our answer by multiplying.^[5]

Example 0.3.2.3

Factor the following polynomials completely over the integers. This means that all of the coefficients in the factors will be integers. While it was decided to avoid fractions in this set of examples, don’t get complacent, though, because fractions will return with a vengeance soon enough.

$36 - 11y - 12y^2$

Solution:

Factor $36 - 11y - 12y^2$ .

Once again, we check for a nontrivial G.C.F. and determine if $36 - 11y - 12y^2$ fits the pattern of a perfect square.

Twice disappointed, we rewrite $36 - 11y - 12y^2 = -12y^2 - 11y + 36$ for notational convenience. We now look for integers $a$ , $b$ , $c$ and $d$ such that $-12y^2 - 11y + 36 = (ay + b)(cy + d)$ . Due to the fact that $ac =-12$ , we know that one of $a$ or $c$ is $\pm 1$ and the other $\mp 12$ OR one of them is $\pm 2$ and the other is $\mp 6$ OR one of them is $\pm 3$ while the other is $\mp 4$ . As their product is $-12$ , however, we know one of them is positive, while the other is negative.

To make matters worse, the constant term $36$ has its fair share of factors, too. Our answers for $b$ and $d$ lie among the pairs $\pm 1$ and $\pm 36$ , $\pm 2$ and $\pm 18$ , $\pm 4$ and $\pm 9$ , or $\pm 6$ .

Because we know one of $a$ or $c$ will be negative, we can simplify our choices for $b$ and $d$ and just look at the positive possibilities. After some guessing and checking,^[6] we determine $(-3y + 4)(4y+9) = -12y^2 - 11y + 36$ .

Example 0.3.2.4

Factor the following polynomials completely over the integers. This means that all of the coefficients in the factors will be integers. While it was decided to avoid fractions in this set of examples, don’t get complacent, though, because fractions will return with a vengeance soon enough.

$18xy^2 - 54xy - 180x$

Solution:

Factor $18xy^2 - 54xy - 180x$ .

Given the G.C.F. of the terms in $18xy^2 - 54xy - 180x$ is $18x$ , we begin the problem by factoring it out first:

$18xy^2 - 54xy - 180x = 18x(y^2 - 3y - 10).$

We now focus our attention on $y^2 - 3y - 10$ . We can take $a$ and $c$ to both be $1$ which yields $(y+b)(y+d) = y^2 - 3y - 10$ .

Our choices for $b$ and $d$ are among the factor pairs of $-10$ : $\pm 1$ and $\mp 10$ or $\pm 2$ and $\mp 5$ , where one of $b$ or $d$ is positive and the other is negative. We find $(y-5)(y+2) = y^2 - 3y - 10$ .

Our final answer is $18xy^2 - 54xy - 180x = 18x(y-5)(y+2)$ .

Example 0.3.2.5

Factor the following polynomials completely over the integers. This means that all of the coefficients in the factors will be integers. While it was decided to avoid fractions in this set of examples, don’t get complacent, though, because fractions will return with a vengeance soon enough.

$2t^3 - 10t^2 + 3t - 15$

Solution:

Factor $2t^3 - 10t^2 + 3t - 15$ .

With $2t^3 - 10t^2 - 3t + 15$ being four terms, we are pretty much resigned to factoring by grouping. The strategy here is to factor out the G.C.F. from two pairs of terms, and see if this reveals a common factor.

If we group the first two terms, we can factor out a $2t^2$ to get $2t^3 - 10t^2 = 2t^2(t-5)$ .

We now try to factor something out of the last two terms that will leave us with a factor of $(t-5)$ . Sure enough, we can factor out a $-3$ from both: $-3t + 15 = -3(t-5)$ . Hence, we get

$\begin{array}{rcl} 2t^3 - 10t^2 - 3t + 15 &=& 2t^2(t-5) - 3(t-5) \\ &=& (2t^2-3)(t-5) \end{array}$

Now the question becomes can we factor $2t^2 - 3$ over the integers? This would require integers $a, b, c$ and $d$ such that $(at + b)(ct + d) = 2t^2 - 3$ . As a result of $ab = 2$ and $cd = -3$ , we aren’t left with many options – in fact, we really have only four choices: $(2t - 1)(t+3)$ , $(2t+1)(t-3)$ , $(2t - 3)(t+1)$ and $(2t+3)(t-1)$ . None of these produce $2t^2 - 3$ – which means it’s irreducible over the integers.

Thus our final answer is $(2t^2-3)(t-5)$ .

Example 0.3.2.6

Factor the following polynomials completely over the integers. This means that all of the coefficients in the factors will be integers. While it was decided to avoid fractions in this set of examples, don’t get complacent, though, because fractions will return with a vengeance soon enough.

$x^4 + 4x^2 + 16$

Solution:

Factor $x^4 + 4x^2 + 16$ .

Our last example, $x^4 + 4x^2 + 16$ , is our old friend from Example 0.3.1. As noted there, it is not a perfect square trinomial, so we could try to reverse the F.O.I.L. process.

This is complicated by the fact that our highest degree term is $x^4$ , so we would have to look at factorizations of the form $(x+b)(x^3+d)$ as well as $(x^2 + b)(x^2 + d)$ . We leave it to the reader to show that neither of those work.

This is an example of where `trying something’ pays off. Even though we’ve stated that it is not a perfect square trinomial, it’s pretty close. Identifying $x^4 = (x^2)^2$ and $16 = 4^2$ , we’d have $(x^2 + 4)^2 = x^4 + 8x^2 + 16$ , but instead of $8x^2$ as our middle term, we only have $4x^2$ . We could add in the extra $4x^2$ we need, but to keep the balance, we’d have to subtract it off. Doing so produces an unexpected opportunity:

$\begin{array}{rclr} x^4 + 4x^2 + 16 & = & x^4 + 4x^2 + 16 + (4x^2 - 4x^2) & \text{Adding and subtracting the same term} \\ & = & x^4 + 8x^2 + 16 - 4x^2 & \text{Rearranging terms} \\ & = & (x^2 + 4)^2 - (2x)^2 & \text{Factoring perfect square trinomial} \\ & = & [(x^2 +4) - 2x][ (x^2 + 4) + 2x] & \text{Difference of Squares: $a= (x^2 + 4)$, $b = 2x$}\\ & = & (x^2 - 2x + 4)(x^2 + 2x + 4) & \text{Rearraging terms} \\ \end{array}$

We leave it to the reader to check that neither $x^2 - 2x + 4$ nor $x^2 + 2x + 4$ factor over the integers, so we are done.

0.3.1 Section Exercises

In Exercises 1 – 30, factor completely over the integers. Check your answer by multiplication.

$2x - 10x^2$
$12t^5 - 8t^3$
$16xy^2 - 12x^2y$
$5(m+3)^2- 4(m+3)^3$
$(2x-1)(x+3) - 4(2x-1)$
$t^2(t-5) + t - 5$
$w^2 - 121$
$49 - 4t^2$
$81t^4 - 16$
$9z^2 - 64y^4$
$(y+3)^2 - 4y^2$
$(x+h)^3 - (x+h)$
$y^2 - 24y + 144$
$25t^2 + 10t + 1$
$12x^3 - 36x^2 + 27x$
$m^4 + 10m^2 + 25$
$27 - 8x^3$
$t^6 +t^3$
$x^2 - 5x - 14$
$y^2 - 12y + 27$
$3t^2 + 16t + 5$
$6x^2 - 23x + 20$
$35+2m - m^2$
$7w - 2w^2 - 3$
$3m^3 + 9m^2 - 12m$
$x^4 + x^2 - 20$
$4(t^2-1)^2 +3(t^2-1) - 10$
$x^3 - 5x^2 - 9x + 45$
$3t^2 + t - 3 - t^3$
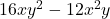
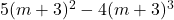
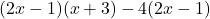
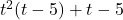
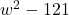
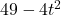
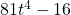
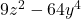
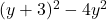
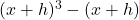
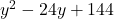
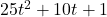
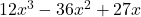
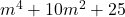
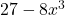
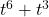
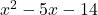
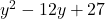
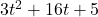
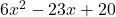
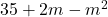
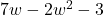
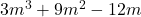
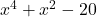
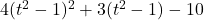
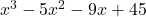
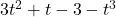
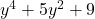$y^4 + 5y^2 + 9$ , Note: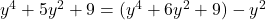 $y^4 + 5y^2 + 9 = (y^4 + 6y^2 + 9) - y^2$

As mentioned in Section 0.1, this is possible, in only one way, thanks to the Fundamental Theorem of Arithmetic. ↵
We'll refer back to this when we get to Section 2.3. ↵
If this isn't immediately obvious, don't worry - in some sense, it shouldn't be. We'll talk more about this later. ↵
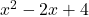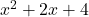Of course, this begs the question, ``How do we know $x^2-2x+4$ and $x^2+2x+4$ are irreducible?'' (We were told so on previously, but no reason was given.) Stay tuned! We'll get back to this in due course. ↵
That's the `checking' part of 'guessing and checking'. ↵
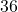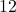Some of these guesses can be more `educated' than others. Due to the fact that the middle term is relatively `small,' we don't expect the `extreme' factors of $36$ and $12$ to appear, for instance. ↵