0.4 Using Interval Notation
0.4.1 Some Basic Set Theory Notions
Definition 0.5
A set is a well-defined collection of objects which are called the elements of the set. Here, `well-defined’ means that it is possible to determine if something belongs to the collection or not, without prejudice.
For example, the collection of letters that make up the word “smolko” is well-defined and is a set, but the collection of the worst Math teachers in the world is not well-defined and therefore is not a set.[1]
In general, there are three ways to describe sets and those methods are listed below.
Ways to Describe Sets
- The Verbal Method: Use a sentence to describe the elements the set.
- The Roster Method: Begin with a left brace `
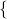 ‘, list each element of the set only once and then end with a right brace `
‘, list each element of the set only once and then end with a right brace `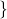 ‘.
‘. - The Set-Builder Method: A combination of the verbal and roster methods using a “dummy variable” such as
 and conditions on that variable.
and conditions on that variable.
Let ![]() be the set described verbally as the set of letters that make up the word “smolko”. A roster description of
be the set described verbally as the set of letters that make up the word “smolko”. A roster description of ![]() is
is ![]() . Note that we listed `o’ only once, even though it appears twice in the word “smolko”. Also, the order of the elements doesn’t matter, so
. Note that we listed `o’ only once, even though it appears twice in the word “smolko”. Also, the order of the elements doesn’t matter, so ![]() is also a roster description of
is also a roster description of ![]() . A set-builder description of
. A set-builder description of ![]() is:
is: ![]() . The way to read this is `The set of elements
. The way to read this is `The set of elements ![]() such that
such that ![]() is a letter in the word “smolko”.’ In each of the above cases, we may use the familiar equals sign `
is a letter in the word “smolko”.’ In each of the above cases, we may use the familiar equals sign `![]() ‘ and write
‘ and write ![]() or
or ![]() .
.
Notice that `m’ is in ![]() but many other letters, such as `q’, are not in
but many other letters, such as `q’, are not in ![]() . We express these ideas of set inclusion and exclusion mathematically using the symbols m
. We express these ideas of set inclusion and exclusion mathematically using the symbols m ![]() (read `m is in
(read `m is in ![]() ‘) and q
‘) and q ![]() (read `q is not in
(read `q is not in ![]() ‘). More precisely, we have the following.
‘). More precisely, we have the following.
Definition 0.6
Let ![]() be a set.
be a set.
- If
 is an element of
is an element of 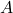 , then we write
, then we write 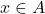 which is read `
which is read ` is in
is in 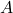 ‘.
‘. - If
 is not an element of
is not an element of 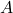 , then we write
, then we write 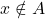 which is read `
which is read ` is not in
is not in 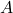 ‘.
‘.
Now let’s consider the set ![]() . A roster description of
. A roster description of ![]() is
is ![]() . Note that by construction, every element of
. Note that by construction, every element of ![]() is also in
is also in ![]() . We express this relationship by stating that the set
. We express this relationship by stating that the set ![]() is a subset of the set
is a subset of the set ![]() , which is written in symbols as
, which is written in symbols as ![]() . The more formal definition is given next.
. The more formal definition is given next.
Definition 0.7
Given sets ![]() and
and ![]() , we say that the set
, we say that the set ![]() is a subset of the set
is a subset of the set ![]() and write `
and write `![]() ‘ if every element in
‘ if every element in ![]() is also an element of
is also an element of ![]() .
.
In our previous example, ![]() yet not vice-versa as `o’
yet not vice-versa as `o’ ![]() but `o’
but `o’ ![]() . Additionally, the set of vowels
. Additionally, the set of vowels ![]() , while it does have an element in common with
, while it does have an element in common with ![]() , is not a subset of
, is not a subset of ![]() . (As an added note,
. (As an added note, ![]() is not a subset of
is not a subset of ![]() , either.) We could, however, build a set which contains both
, either.) We could, however, build a set which contains both ![]() and
and ![]() as subsets by gathering all of the elements in both
as subsets by gathering all of the elements in both ![]() and
and ![]() together into a single set, say
together into a single set, say ![]() . Then
. Then ![]() and
and ![]() . The set
. The set ![]() we have built is called the union of the sets
we have built is called the union of the sets ![]() and
and ![]() and is denoted
and is denoted ![]() . Furthermore,
. Furthermore, ![]() and
and ![]() aren’t completely different sets as they both contain the letter `o.’ The intersection of two sets is the set of elements (if any) the two sets have in common. In this case, the intersection of
aren’t completely different sets as they both contain the letter `o.’ The intersection of two sets is the set of elements (if any) the two sets have in common. In this case, the intersection of ![]() and
and ![]() is
is ![]() , written
, written ![]() . We formalize these ideas below.
. We formalize these ideas below.
The key words in Definition 0.8 to focus on are the conjunctions: `intersection’ corresponds to `and’ meaning the elements have to be in both sets to be in the intersection, whereas `union’ corresponds to `or’ meaning the elements have to be in one set, or the other set (or both). Please note that this mathematical use of the word `or’ differs than how we use `or’ in spoken English. In Math, we use the inclusive or which allows for the element to be in both sets. At a restaurant if you’re asked “Do you want fries or a salad?” you must pick one and only one. This is known as the exclusive or and it plays a role in other Math classes. For our purposes it is good enough to say that for an element to belong to the union of two sets it must belong to at least one of them.
Returning to the sets ![]() and
and ![]() above,
above, ![]() .[2] Their intersection, however, creates a bit of notational awkwardness due to the fact that
.[2] Their intersection, however, creates a bit of notational awkwardness due to the fact that ![]() and
and ![]() have no elements in common. While we could write
have no elements in common. While we could write ![]() , this sort of thing happens often enough that we give the set with no elements a name.
, this sort of thing happens often enough that we give the set with no elements a name.
As promised, the empty set is the set containing no elements because no matter what ![]() is,
is, ![]() . Like the number
. Like the number ![]() , the empty set plays a vital role in mathematics.[3] We introduce it here more as a symbol of convenience as opposed to a contrivance[4] because saying that
, the empty set plays a vital role in mathematics.[3] We introduce it here more as a symbol of convenience as opposed to a contrivance[4] because saying that ![]() is unambiguous whereas
is unambiguous whereas ![]() looks like a typographical error.
looks like a typographical error.
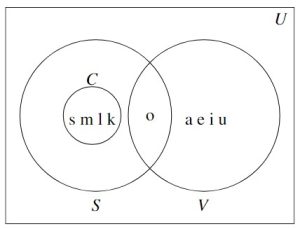
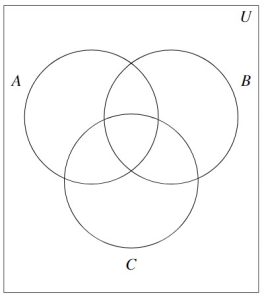
A nice way to visualize the relationships between sets and set operations is to draw a Venn Diagram. A Venn Diagram for the sets ![]() ,
, ![]() and
and ![]() is drawn below.
is drawn below.
In the Venn Diagram above we have three circles – one for each of the sets ![]() ,
, ![]() and
and ![]() . We visualize the area enclosed by each of these circles as the elements of each set. Here, we’ve spelled out the elements for definitiveness. Notice that the circle representing the set
. We visualize the area enclosed by each of these circles as the elements of each set. Here, we’ve spelled out the elements for definitiveness. Notice that the circle representing the set ![]() is completely inside the circle representing
is completely inside the circle representing ![]() . This is a geometric way of showing that
. This is a geometric way of showing that ![]() . Also, notice that the circles representing
. Also, notice that the circles representing ![]() and
and ![]() overlap on the letter `o’. This common region is how we visualize
overlap on the letter `o’. This common region is how we visualize ![]() . Notice that because
. Notice that because ![]() , the circles which represent
, the circles which represent ![]() and
and ![]() have no overlap whatsoever.
have no overlap whatsoever.
All of these circles lie in a rectangle labeled ![]() for the `universal’ set. A universal set contains all of the elements under discussion, so it could always be taken as the union of all of the sets in question, or an even larger set. In this case, we could take
for the `universal’ set. A universal set contains all of the elements under discussion, so it could always be taken as the union of all of the sets in question, or an even larger set. In this case, we could take ![]() or
or ![]() as the set of letters in the entire alphabet. The reader may well wonder if there is an ultimate universal set which contains everything. The short answer is `no’ and we refer you once again to Russell’s Paradox. The usual triptych of Venn Diagrams indicating generic sets
as the set of letters in the entire alphabet. The reader may well wonder if there is an ultimate universal set which contains everything. The short answer is `no’ and we refer you once again to Russell’s Paradox. The usual triptych of Venn Diagrams indicating generic sets ![]() and
and ![]() along with
along with ![]() and
and ![]() is given below.
is given below.
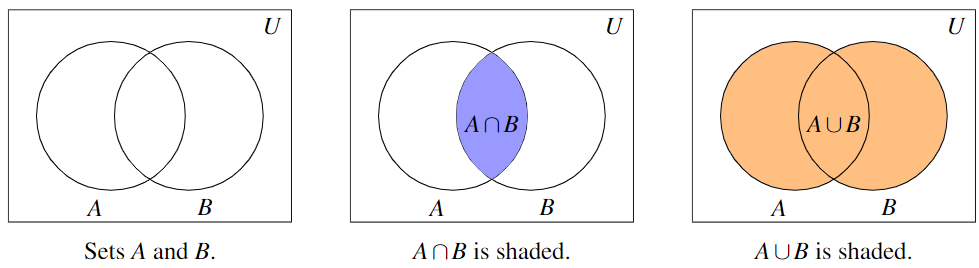
Three two-circle Venn Diagrams. In each graph the left circle is labeled A, the right circle is labeled B and the rectangle is labeled with a U in the upper right corner. The first diagram has no shading. The center diagram has the region where circles A and B overlap shaded blue. The third diagram has all of regions in circles A or B shaded orange.
The one major limitation of Venn Diagrams is that they become unwieldy if more than four sets need to be drawn simultaneously within the same universal set. This idea is explored in the Exercises.
0.4.2 Special Subsets of Real Numbers
Recall in Section 0.1 we defined some special subsets of real numbers.
Special Subsets of Real Numbers
- The Natural Numbers:
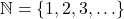 . The periods of ellipsis `
. The periods of ellipsis ` ‘ here indicate that the natural numbers contain 1, 2, 3 `and so forth’.
‘ here indicate that the natural numbers contain 1, 2, 3 `and so forth’. - The Whole Numbers:
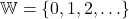 .
. - The Integers:
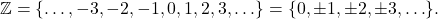
- The Rational Numbers:
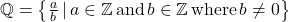 . Rational numbers are the ratios of integers where the denominator is not zero. It turns out that another way to describe the rational numbers is:
. Rational numbers are the ratios of integers where the denominator is not zero. It turns out that another way to describe the rational numbers is: 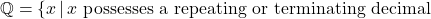
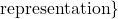
- The Irrational Numbers:
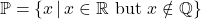 . That is, an irrational number is a real number, which isn’t rational. Said differently,
. That is, an irrational number is a real number, which isn’t rational. Said differently, 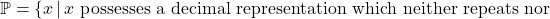
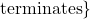
It is time to put all of this together in an example.
Example 0.4.1
Example 0.4.1.1
Write a roster description for ![]() and
and ![]() .
.
Solution:
Write a roster description for ![]() and
and ![]() .
.
To construct roster descriptions for each of these sets, we need to list their elements. Starting with the set ![]() , we substitute natural number values
, we substitute natural number values ![]() into the formula
into the formula ![]() . For
. For ![]() we get
we get ![]() , for
, for ![]() we get
we get ![]() , for
, for ![]() we get
we get ![]() and for
and for ![]() we get
we get ![]() .
.
Hence ![]() describes the powers of
describes the powers of ![]() , thus a roster description for
, thus a roster description for ![]() is
is ![]() where the `
where the `![]() ‘ indicates that the pattern continues.[5]
‘ indicates that the pattern continues.[5]
Proceeding in the same way, we generate elements in ![]() by plugging in integer values of
by plugging in integer values of ![]() into the formula
into the formula ![]() . Starting with
. Starting with ![]() we obtain
we obtain ![]() . For
. For ![]() we get
we get ![]() , for
, for ![]() we get
we get ![]() for
for ![]() , we get
, we get ![]() and for
and for ![]() we get
we get ![]() . As
. As ![]() moves through the integers,
moves through the integers, ![]() produces all of the even integers.[6]
produces all of the even integers.[6]
A roster description for ![]() is
is ![]() .
.
Example 0.4.1.2
Write a verbal description for ![]() .
.
Solution:
Write a roster description for ![]() and
and ![]() .
.
One way to verbally describe ![]() is to say that
is to say that ![]() is the `set of all squares of real numbers’. While this isn’t incorrect, we’d like to take this opportunity to delve a little deeper. What makes the set
is the `set of all squares of real numbers’. While this isn’t incorrect, we’d like to take this opportunity to delve a little deeper. What makes the set ![]() a little trickier to wrangle than the sets
a little trickier to wrangle than the sets ![]() or
or ![]() above is that the dummy variable here,
above is that the dummy variable here, ![]() , runs through all real numbers. Unlike the natural numbers or the integers, the real numbers cannot be listed in any methodical way.[7] Nevertheless, we can select some real numbers, square them and get a sense of what kind of numbers lie in
, runs through all real numbers. Unlike the natural numbers or the integers, the real numbers cannot be listed in any methodical way.[7] Nevertheless, we can select some real numbers, square them and get a sense of what kind of numbers lie in ![]() . For
. For ![]() ,
, ![]() so
so ![]() is in
is in ![]() , as are
, as are ![]() and
and ![]() . Even things like
. Even things like ![]() and
and ![]() are in
are in ![]() .
.
So suppose ![]() . What can be said about
. What can be said about ![]() ? We know there is some real number
? We know there is some real number ![]() so that
so that ![]() . As
. As ![]() for any real number
for any real number ![]() , we know
, we know ![]() . This tells us that everything in
. This tells us that everything in ![]() is a non-negative real number.[8] This begs the question: are all of the non-negative real numbers in
is a non-negative real number.[8] This begs the question: are all of the non-negative real numbers in ![]() ? Suppose
? Suppose ![]() is a non-negative real number, that is,
is a non-negative real number, that is, ![]() . If
. If ![]() were in
were in ![]() , there would be a real number
, there would be a real number ![]() so that
so that ![]() . As you may recall, we can solve
. As you may recall, we can solve ![]() by `extracting square roots’:
by `extracting square roots’: ![]() . Because
. Because ![]() ,
, ![]() is a real number.[9] Moreover,
is a real number.[9] Moreover, ![]() so
so ![]() is the square of a real number which means
is the square of a real number which means ![]() .
.
Hence, ![]() is the set of non-negative real numbers.
is the set of non-negative real numbers.
Example 0.4.1.3a
Let ![]() .
.
Which elements of ![]() are natural numbers? Rational numbers? Real numbers?
are natural numbers? Rational numbers? Real numbers?
Solution:
Let ![]() .
.
Which elements of ![]() are natural numbers? Rational numbers? Real numbers?
are natural numbers? Rational numbers? Real numbers?
The set ![]() contains no natural numbers. Clearly
contains no natural numbers. Clearly ![]() is a rational number as is
is a rational number as is ![]() (which can be written as
(which can be written as ![]() ). It’s the last two numbers listed in
). It’s the last two numbers listed in ![]() ,
, ![]() and
and ![]() , that warrant some discussion. First, recall that the `line’ over the digits
, that warrant some discussion. First, recall that the `line’ over the digits ![]() in
in ![]() (called the vinculum) indicates that these digits repeat, so it is a rational number.[10] As for the number
(called the vinculum) indicates that these digits repeat, so it is a rational number.[10] As for the number ![]() , the `
, the `![]() ‘ indicates the pattern of adding an extra `
‘ indicates the pattern of adding an extra `![]() ‘ followed by a `
‘ followed by a `![]() ‘ is what defines this real number. Despite the fact there is a pattern to this decimal, this decimal is not repeating, so it is not a rational number – it is, in fact, an irrational number. All of the elements of
‘ is what defines this real number. Despite the fact there is a pattern to this decimal, this decimal is not repeating, so it is not a rational number – it is, in fact, an irrational number. All of the elements of ![]() are real numbers, because all of them can be expressed as decimals (remember that
are real numbers, because all of them can be expressed as decimals (remember that ![]() ).
).
Example 0.4.1.3b
Let ![]() .
.
Determine ![]() ,
, ![]() and
and ![]() .
.
Solution:
Let ![]() .
.
Determine ![]() ,
, ![]() and
and ![]() .
.
The set ![]() is another way of saying we are looking for the set of numbers in
is another way of saying we are looking for the set of numbers in ![]() which are whole numbers. As
which are whole numbers. As ![]() contains no whole numbers,
contains no whole numbers, ![]() . Similarly,
. Similarly, ![]() is looking for the set of numbers in
is looking for the set of numbers in ![]() which are integers.
which are integers. ![]() is the only integer in
is the only integer in ![]() , so
, so ![]() . For the set
. For the set ![]() , as discussed in part (a), the number
, as discussed in part (a), the number ![]() is irrational, thus
is irrational, thus ![]() .
.
Example 0.4.1.4
What is another name for ![]() ? What about
? What about ![]() ?
?
Solution:
What is another name for ![]() ? What about
? What about ![]() ?
?
The set ![]() is the union of the set of natural numbers with the set of rational numbers. Because every natural number is a rational number,
is the union of the set of natural numbers with the set of rational numbers. Because every natural number is a rational number, ![]() doesn’t contribute any new elements to
doesn’t contribute any new elements to ![]() , so
, so ![]() .[11] For the set
.[11] For the set ![]() , we note that every real number is either rational or not, hence
, we note that every real number is either rational or not, hence ![]() , pretty much by the definition of the set
, pretty much by the definition of the set ![]() .
.
0.4.3 The Real Number Line and Interval Notation
As you may recall, we often visualize the set of real numbers ![]() as a line where each point on the line corresponds to one and only one real number. Given two different real numbers
as a line where each point on the line corresponds to one and only one real number. Given two different real numbers ![]() and
and ![]() , we write
, we write ![]() if
if ![]() is located to the left of
is located to the left of ![]() on the number line, as shown below.
on the number line, as shown below.
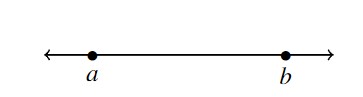
While this notion seems innocuous, it is worth pointing out that this convention is rooted in two deep properties of real numbers. The first property is that ![]() is complete. This means that there are no `holes’ or `gaps’ in the real number line.[12] Another way to think about this is that if you choose any two distinct (different) real numbers, and look between them, you’ll find a solid line segment (or interval) consisting of infinitely many real numbers. The next result tells us what types of numbers we can expect to find.
is complete. This means that there are no `holes’ or `gaps’ in the real number line.[12] Another way to think about this is that if you choose any two distinct (different) real numbers, and look between them, you’ll find a solid line segment (or interval) consisting of infinitely many real numbers. The next result tells us what types of numbers we can expect to find.
Density Property of  and
and  in
in 
Between any two distinct real numbers, there is at least one rational number and one irrational number. It then follows that between any two distinct real numbers there will be infinitely many rational and infinitely many irrational numbers.
The root word `dense’ here communicates the idea that rationals and irrationals are `thoroughly mixed’ into ![]() . The reader is encouraged to think about how one would find both a rational and an irrational number between, say,
. The reader is encouraged to think about how one would find both a rational and an irrational number between, say, ![]() and
and ![]() . Once you’ve done that, try doing the same thing for the numbers
. Once you’ve done that, try doing the same thing for the numbers ![]() and
and ![]() . (`Try’ is the operative word, here.)
. (`Try’ is the operative word, here.)
The second property ![]() possesses that lets us view it as a line is that the set is totally ordered. This means that given any two real numbers
possesses that lets us view it as a line is that the set is totally ordered. This means that given any two real numbers ![]() and
and ![]() , either
, either ![]() ,
, ![]() or
or ![]() which allows us to arrange the numbers from least (left) to greatest (right). This property is given below.
which allows us to arrange the numbers from least (left) to greatest (right). This property is given below.
Segments of the real number line are called intervals. They play a huge role not only in this text but also in the Calculus curriculum so we need a concise way to describe them. We start by examining a few examples of the interval notation associated with some specific sets of numbers.

As you can glean from the table, for intervals with finite endpoints we start by writing `left endpoint, right endpoint’. We use square brackets, `![]() ‘ or `
‘ or `![]() ‘, if the endpoint is included in the interval. This corresponds to a `filled-in’ or `closed’ dot on the number line to indicate that the number is included in the set. Otherwise, we use parentheses, `
‘, if the endpoint is included in the interval. This corresponds to a `filled-in’ or `closed’ dot on the number line to indicate that the number is included in the set. Otherwise, we use parentheses, `![]() ‘ or `
‘ or `![]() ‘ that correspond to an `open’ circle which indicates that the endpoint is not part of the set. If the interval does not have finite endpoints, we use the symbol
‘ that correspond to an `open’ circle which indicates that the endpoint is not part of the set. If the interval does not have finite endpoints, we use the symbol ![]() to indicate that the interval extends indefinitely to the left and the symbol
to indicate that the interval extends indefinitely to the left and the symbol ![]() to indicate that the interval extends indefinitely to the right. As infinity is a concept, and not a number, we always use parentheses when using these symbols in interval notation, and use the appropriate arrow to indicate that the interval extends indefinitely in one or both directions. We summarize all of the possible cases in one convenient table below.[13]
to indicate that the interval extends indefinitely to the right. As infinity is a concept, and not a number, we always use parentheses when using these symbols in interval notation, and use the appropriate arrow to indicate that the interval extends indefinitely in one or both directions. We summarize all of the possible cases in one convenient table below.[13]
Interval Notation
Let ![]() and
and ![]() be real numbers with
be real numbers with ![]() .
.

Intervals of the forms ![]() and
and ![]() are said to be open intervals. Those of the forms
are said to be open intervals. Those of the forms ![]() and
and ![]() are said to be closed intervals.
are said to be closed intervals.
Unfortunately, the words `open’ and `closed’ are not antonyms here because the empty set ![]() and the set
and the set ![]() are simultaneously open and closed[14] while the intervals
are simultaneously open and closed[14] while the intervals ![]() and
and ![]() are neither open nor closed. The inclusion or exclusion of an endpoint might seem like a terribly small thing to fuss about but these sorts of technicalities in the language become important in Calculus so we feel the need to put this material in the Precalculus book.
are neither open nor closed. The inclusion or exclusion of an endpoint might seem like a terribly small thing to fuss about but these sorts of technicalities in the language become important in Calculus so we feel the need to put this material in the Precalculus book.
We close this section with an example that ties together some of the concepts presented earlier. Specifically, we demonstrate how to use interval notation along with the concepts of union and intersection to describe a variety of sets on the real number line. In many sections of the text to come you will need to be fluent with this notation so take the time to study it deeply now.
Example 0.4.2
Example 0.4.2.1a
Express the following sets of numbers using interval notation.
![]()
Solution:
Express ![]() using interval notation.
using interval notation.
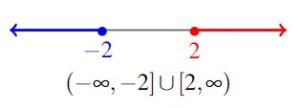
The best way to proceed here is to graph the set of numbers on the number line and glean the answer from it. The inequality ![]() corresponds to the interval
corresponds to the interval ![]() and the inequality
and the inequality ![]() corresponds to the interval
corresponds to the interval ![]() . The `or’ in
. The `or’ in ![]() tells us that we are looking for the union of these two intervals, so our answer is
tells us that we are looking for the union of these two intervals, so our answer is ![]() .
.
Example 0.4.2.1b
Express the following sets of numbers using interval notation.
![]()
Solution:
Express ![]() using interval notation.
using interval notation.
For the set ![]() , we need the real numbers less than (to the left of)
, we need the real numbers less than (to the left of) ![]() that are simultaneously greater than (to the right of)
that are simultaneously greater than (to the right of) ![]() , including
, including ![]() but excluding
but excluding ![]() . This yields
. This yields ![]() .
.

Example 0.4.2.1c
Express the following sets of numbers using interval notation.
![]()
Solution:
Express ![]() using interval notation.
using interval notation.
For the set ![]() , we proceed as before and exclude both
, we proceed as before and exclude both ![]() and
and ![]() from our set. (Refer back to Section 0.1 for a discussion about
from our set. (Refer back to Section 0.1 for a discussion about ![]() ) This breaks the number line into three intervals,
) This breaks the number line into three intervals, ![]() ,
, ![]() and
and ![]() . Because the set describes real numbers which come from the first, second or third interval, we have
. Because the set describes real numbers which come from the first, second or third interval, we have ![]() .
.

Example 0.4.2.1d
Express the following sets of numbers using interval notation.
![]()
Solution:
Express ![]() using interval notation.
using interval notation.
Graphing the set ![]() yields the interval
yields the interval ![]() along with the single number 5. While we could express this single point as
along with the single number 5. While we could express this single point as ![]() , it is customary to write a single point as a `singleton set’, so in our case we have the set
, it is customary to write a single point as a `singleton set’, so in our case we have the set ![]() . This means that our final answer is written
. This means that our final answer is written ![]() .
.

Example 0.4.2.2
Let ![]() and
and ![]() . Determine
. Determine ![]() and
and ![]() , express your answer using interval notation.
, express your answer using interval notation.
Solution:
Let ![]() and
and ![]() . Determine
. Determine ![]() and
and ![]() , express your answer using interval notation.
, express your answer using interval notation.
We start by graphing ![]() and
and ![]() on the number line. To find
on the number line. To find ![]() , we need to find the numbers common to both
, we need to find the numbers common to both ![]() and
and ![]() ; in other words, we need to find the overlap of the two intervals. Clearly, everything between
; in other words, we need to find the overlap of the two intervals. Clearly, everything between ![]() and
and ![]() is in both
is in both ![]() and
and ![]() . However, because
. However, because ![]() is in
is in ![]() but not in
but not in ![]() ,
, ![]() is not in the intersection. Similarly, because
is not in the intersection. Similarly, because ![]() is in
is in ![]() but not in
but not in ![]() , it isn’t in the intersection either. Hence,
, it isn’t in the intersection either. Hence, ![]() .
.
To find ![]() , we need to find the numbers in at least one of
, we need to find the numbers in at least one of ![]() or
or ![]() . Graphically, we shade
. Graphically, we shade ![]() and
and ![]() along with it. Notice here that even though
along with it. Notice here that even though ![]() isn’t in
isn’t in ![]() , it is in
, it is in ![]() , so it’s in the union along with all of the other elements of
, so it’s in the union along with all of the other elements of ![]() between
between ![]() and
and ![]() . A similar argument goes for the inclusion of
. A similar argument goes for the inclusion of ![]() in the union. The result of shading both
in the union. The result of shading both ![]() and
and ![]() together gives us
together gives us ![]() .
.

0.4.4 Section Exercises
-
- Write a verbal description for
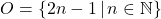 .
. - Write a roster description for
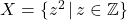 .
. - Let
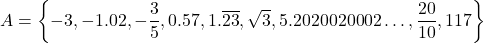
- List the elements of
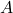 which are natural numbers.
which are natural numbers. - List the elements of
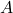 which are irrational numbers.
which are irrational numbers. - Find
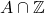
- Find
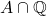
- List the elements of
- Fill in the chart below.

In Exercises 5 – 10, determine the indicated intersection or union and simplify if possible. Express your answers in interval notation.
In Exercises 11 – 22, write the set using interval notation.
For Exercises 23 – 28, use the blank Venn Diagram below with
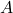 ,
,  , and
, and  in it as a guide to help you shade the following sets.
in it as a guide to help you shade the following sets.
- Explain how your answers to problems 27 and 28 show
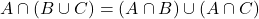 . Phrased differently, this shows `intersection distributes over union.’ Discuss with your classmates if `union’ distributes over `intersection.’ Use a Venn Diagram to support your answer.
. Phrased differently, this shows `intersection distributes over union.’ Discuss with your classmates if `union’ distributes over `intersection.’ Use a Venn Diagram to support your answer. - Show that
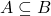 if and only if
if and only if 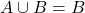 .
. - Let
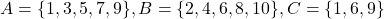 and
and 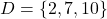 . Draw one Venn Diagram that shows all four of these sets. What sort of difficulties do you encounter?
. Draw one Venn Diagram that shows all four of these sets. What sort of difficulties do you encounter?
- Write a verbal description for
Section 0.4 Exercise Answers can be found in the Appendix … Coming soon
- For a more thought-provoking example, consider the collection of all things that do not contain themselves - this leads to the famous paradox known as Russell's Paradox. ↵
- Which just so happens to be the same set as
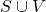 . ↵
. ↵ - Sadly, the full extent of the empty set's role will not be explored in this text. ↵
- Actually, the empty set can be used to generate numbers - mathematicians can create something from nothing! ↵
- This isn't the most precise way to describe this set - it's always dangerous to use `
 ' because we assume that the pattern is clearly demonstrated and thus made evident to the reader. Formulas are more precise because the pattern is clear. ↵
' because we assume that the pattern is clearly demonstrated and thus made evident to the reader. Formulas are more precise because the pattern is clear. ↵ - This shouldn't be too surprising, as an even integer is defined to be an integer multiple of
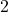 . ↵
. ↵ - This is a nontrivial statement. Interested readers are directed to a discussion of Cantor's Diagonal Argument. ↵
- This means
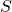 is a subset of the non-negative real numbers. ↵
is a subset of the non-negative real numbers. ↵ - This is called the `square root closed property' of the non-negative real numbers. ↵
- So
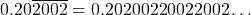 . ↵
. ↵ - In fact, anytime
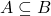 ,
, 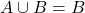 and vice-versa. See the exercises. ↵
and vice-versa. See the exercises. ↵ - Alas, this intuitive feel for what it means to be `complete' is as good as it gets at this level. Completeness is given a much more precise meaning later in courses like Analysis and Topology. ↵
- The importance of understanding interval notation in this book and also in Calculus cannot be overstated so please do yourself a favor and memorize this chart. ↵
- You don't need to worry about that fact until you take an advanced course in Topology. ↵
A well-defined collection of objects.
A set A is a subset of set B, if every element in A is also an element of B
The intersection of two sets A and B are the set of elements that are in BOTH set A and set B
The union of two sets A and B is the set containing the elements in set A or set B or in both A and B.
The set which contains no elements

