1.4 Absolute Value Functions
1.4.1 Graphs of Absolute Value Functions
In Section 1.3.1, we revisited lines in a function context. In this section, we revisit the absolute value in a similar manner, so it may be useful to refresh yourself with the basics in Section 0.5.2. Recall that the absolute value of a real number ![]() , denoted
, denoted ![]() , can be defined as the distance from
, can be defined as the distance from ![]() to
to ![]() on the real number line.[1] This definition is very useful for several applications, and lends itself well to solving equations and inequalities such as
on the real number line.[1] This definition is very useful for several applications, and lends itself well to solving equations and inequalities such as ![]() or
or ![]() .
.
We now wish to explore solving more complicated equations and inequalities, such as ![]() and
and ![]() . We’ll approach these types of problems from a function standpoint and use the interplay between the graphical and analytical representations of these functions to obtain solutions. The key to this section is understanding the absolute value from that function (or procedural) standpoint.
. We’ll approach these types of problems from a function standpoint and use the interplay between the graphical and analytical representations of these functions to obtain solutions. The key to this section is understanding the absolute value from that function (or procedural) standpoint.
Consider a real number ![]() such as
such as ![]() ,
, ![]() or
or ![]() . When computing absolute values, we find
. When computing absolute values, we find ![]() ,
, ![]() and
and ![]() . In general, if
. In general, if ![]() , the absolute value function does nothing to change the input, so
, the absolute value function does nothing to change the input, so ![]() . On the other hand, if
. On the other hand, if ![]() , say
, say ![]() ,
, ![]() or
or ![]() , we get
, we get ![]() ,
, ![]() and
and ![]() . That is, if
. That is, if ![]() ,
, ![]() returns the exact opposite of the input
returns the exact opposite of the input ![]() , so
, so ![]() .
.
Putting these two observations together, we have the following.
In Definition 1.12, it is absolutely essential to read `![]() ‘ as `the opposite of
‘ as `the opposite of ![]() ‘ as opposed to `negative
‘ as opposed to `negative ![]() ‘ in order to avoid serious errors later. To see that this description agrees with our previous experience, consider
‘ in order to avoid serious errors later. To see that this description agrees with our previous experience, consider ![]() . Given that
. Given that ![]() , we use the rule
, we use the rule ![]() . Hence,
. Hence, ![]() . Likewise,
. Likewise, ![]() . To compute
. To compute ![]() , we note that
, we note that ![]() we use the rule
we use the rule ![]() in this case. We get
in this case. We get ![]() (the opposite of
(the opposite of ![]() ), so
), so ![]() .
.
Another way to view Definition 1.12 is to think of ![]() and
and ![]() . That is,
. That is, ![]() multiplies negative inputs by
multiplies negative inputs by ![]() and non-negative inputs by
and non-negative inputs by ![]() . This viewpoint is especially useful in graphing
. This viewpoint is especially useful in graphing ![]() .
.
For ![]() ,
, ![]() , so the graph of
, so the graph of ![]() is the graph of
is the graph of ![]() : a line with slope
: a line with slope ![]() and
and ![]() -intercept
-intercept ![]() .
.
Likewise, for ![]() ,
, ![]() , so the graph of
, so the graph of ![]() is the graph of
is the graph of ![]() : a line with slope
: a line with slope ![]() and
and ![]() -intercept
-intercept ![]() .
.
Next, we graph each piece and then put them together. Note that when graphing ![]() for
for ![]() , we have a hole at
, we have a hole at ![]() because the inequality
because the inequality ![]() is strict. However, the point
is strict. However, the point ![]() is included in the graph of
is included in the graph of ![]() for
for ![]() , so there is no hole in our final graph.
, so there is no hole in our final graph.


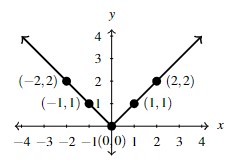
The graph of ![]() is a very distinctive `
is a very distinctive `![]() ‘ shape and is worth remembering. The point
‘ shape and is worth remembering. The point ![]() on the graph is called the vertex. This terminology makes sense from a geometric viewpoint because
on the graph is called the vertex. This terminology makes sense from a geometric viewpoint because ![]() is the point where two lines meet to form an angle. We will also see this term used in Section 2.1 where, more generally, it corresponds to the graphical location of the sole maximum or minimum of a quadratic function.
is the point where two lines meet to form an angle. We will also see this term used in Section 2.1 where, more generally, it corresponds to the graphical location of the sole maximum or minimum of a quadratic function.
We put Definition 1.12 to good use in the next example and review the basics of graphing along the way.
Example 1.4.1
Example 1.4.1.1
For each of the functions below, analytically find the zeros of the function and the axis intercepts of the graph, if any exist. Rewrite the function using Definition 1.12 as a piecewise-defined function and sketch its graph. From the graph, determine the vertex, find the range of the function and any extrema, and then list the intervals over which the function is increasing, decreasing or constant.
![]()
Solution:
In what follows below, we will be doing quite a bit of substitution. As we have mentioned before, when substituting one expression in for another, the use of parentheses or other grouping symbols is highly recommended. Also, the dependent variable wasn’t specified so we use the default ![]() in each case.
in each case.
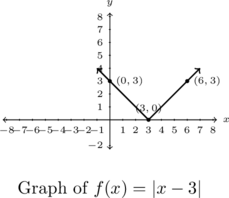
Analyze ![]() .
.
To find the zeros of ![]() , we solve
, we solve ![]() or
or ![]() . We get
. We get ![]() so the sole
so the sole ![]() -intercept of the graph of
-intercept of the graph of ![]() is
is ![]() .
.
To find the ![]() -intercept, we compute
-intercept, we compute ![]() and obtain
and obtain ![]() . Using Definition 1.12 to rewrite the expression for
. Using Definition 1.12 to rewrite the expression for ![]() means that we substitute the expression
means that we substitute the expression ![]() in for
in for ![]() and simplify. Note that when substituting the
and simplify. Note that when substituting the ![]() in for
in for ![]() , we do so for every instance of
, we do so for every instance of ![]() — both in the formula (output) as well as the inequality (input).
— both in the formula (output) as well as the inequality (input).
![]()
As both pieces of the graph of ![]() are lines, we need just two points for each piece. We already have two points for the graph:
are lines, we need just two points for each piece. We already have two points for the graph: ![]() and
and ![]() . These two points both lie on the line
. These two points both lie on the line ![]() but the strictness of the inequality means
but the strictness of the inequality means ![]() only for
only for ![]() , not
, not ![]() , so we would have a hole at
, so we would have a hole at ![]() instead of a point there.
instead of a point there.
For ![]() ,
, ![]() , so the hole we thought we had at
, so the hole we thought we had at ![]() gets plugged because
gets plugged because ![]() . We need just one more point for
. We need just one more point for ![]() where
where ![]() and choose somewhat arbitrarily
and choose somewhat arbitrarily ![]() . We find
. We find ![]() so our final point on the graph is
so our final point on the graph is ![]() .
.
Now that we have a complete graph,[2] we see that the vertex is ![]() and the range is
and the range is ![]() . The minimum of
. The minimum of ![]() is
is ![]() when
when ![]() and
and ![]() has no maximum. Also,
has no maximum. Also, ![]() is decreasing over
is decreasing over ![]() and increasing on
and increasing on ![]() .
.
The graph is given below.
Example 1.4.1.2
For each of the functions below, analytically find the zeros of the function and the axis intercepts of the graph, if any exist. Rewrite the function using Definition 1.12 as a piecewise-defined function and sketch its graph. From the graph, determine the vertex, find the range of the function and any extrema, and then list the intervals over which the function is increasing, decreasing or constant.
![]()
Solution:
In what follows below, we will be doing quite a bit of substitution. As we have mentioned before, when substituting one expression in for another, the use of parentheses or other grouping symbols is highly recommended. Also, the dependent variable wasn’t specified so we use the default ![]() in each case.
in each case.
Analyze ![]() .
.
To find the zeros of ![]() , we solve
, we solve ![]() and get
and get ![]() or
or ![]() . Hence, the
. Hence, the ![]() -intercepts of the graph of
-intercepts of the graph of ![]() are
are ![]() and
and ![]() .
.
To find the ![]() -intercept, we compute
-intercept, we compute ![]() and get
and get ![]() . To rewrite
. To rewrite ![]() has a piecewise defined function, we first substitute
has a piecewise defined function, we first substitute ![]() in for
in for ![]() in Definition 1.12 to get a piecewise definition of
in Definition 1.12 to get a piecewise definition of ![]() . This breaks the domain into two pieces:
. This breaks the domain into two pieces: ![]() and
and ![]() . For
. For ![]() ,
, ![]() , so
, so ![]() . Likewise, for
. Likewise, for ![]() ,
, ![]() so
so ![]() .
.
![]()
Once again, we have two lines to graph, but in this case we have three points: ![]() ,
, ![]() and
and ![]() . Both
. Both ![]() and
and ![]() lie on
lie on ![]() , but
, but ![]() only for
only for ![]() . This would yield a hole at
. This would yield a hole at ![]() , but, just like in the previous example, the hole is plugged thanks to the second piece of the function because
, but, just like in the previous example, the hole is plugged thanks to the second piece of the function because ![]() .
.
We also pick up the second ![]() -intercept,
-intercept, ![]() and this helps us complete our graph.
and this helps us complete our graph.
We see that the vertex is ![]() and the range is
and the range is ![]() . The minimum of
. The minimum of ![]() is
is ![]() at
at ![]() and there is no maximum. Also,
and there is no maximum. Also, ![]() is decreasing on
is decreasing on ![]() and increasing on
and increasing on ![]() .
.
The graph of ![]() is shown below.
is shown below.
Example 1.4.1.3
For each of the functions below, analytically find the zeros of the function and the axis intercepts of the graph, if any exist. Rewrite the function using Definition 1.12 as a piecewise-defined function and sketch its graph. From the graph, determine the vertex, find the range of the function and any extrema, and then list the intervals over which the function is increasing, decreasing or constant.
![]()
Solution:
In what follows below, we will be doing quite a bit of substitution. As we have mentioned before, when substituting one expression in for another, the use of parentheses or other grouping symbols is highly recommended. Also, the dependent variable wasn’t specified so we use the default ![]() in each case.
in each case.
Analyze ![]() .
.
Solving ![]() gives
gives ![]() or
or ![]() . We get two zeros:
. We get two zeros: ![]() and
and ![]() which correspond to two
which correspond to two ![]() -intercepts:
-intercepts: ![]() and
and ![]() .
.
We find ![]() so our
so our ![]() -intercept is
-intercept is ![]() . To rewrite
. To rewrite ![]() as a piecewise defined function, we first rewrite
as a piecewise defined function, we first rewrite ![]() as a piecewise function. Substituting the expression
as a piecewise function. Substituting the expression ![]() in for
in for ![]() in Definition 1.12 gives:
in Definition 1.12 gives:
![Rendered by QuickLaTeX.com \[ \begin{array}{ccc} |2u - 1| = \left\{ \begin{array}{rc} -(2u - 1) & \text{if }2u - 1 < 0 \\ 2u - 1 & \text{if }2u - 1 \geq 0} \\ \end{array} \right. & \longrightarrow & |2u - 1| = \left\{ \begin{array}{rc} -2u + 1 & \text{if } u < \dfrac{1}{2} \\[8pt] 2u - 1 & \text{if } u \geq \dfrac{1}{2}\\ \end{array} \right. \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-fc0a737b3551cbfe35450f5133eb796c_l3.png)
Hence, for ![]() ,
, ![]() so
so
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl}h(u) &=& |2u - 1| - 3 \\ &=& (-2u + 1) - 3 \\ &=& -2u - 2. \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-61422f72cf61a15ece5e8f0ba526cb90_l3.png)
Likewise, for ![]() ,
, ![]() so
so
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} h(u) &=& |2u - 1| - 3 \\ &=& (2u - 1) - 3 \\ &=& 2u - 4. \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f1fe38a0da8c9a8b69fc992540008df5_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{array}{ccc} h(u) = |2u - 1| - 3 = \left\{ \begin{array}{rc} (-2u + 1) - 3 & \text{if } u < \dfrac{1}{2} \\[8pt] (2u - 1) - 3 & \text{if }u \geq \dfrac{1}{2} \\ \end{array} \right. & \longrightarrow & h(u) = \left\{ \begin{array}{rc} -2u - 2 & \text{if } u < \dfrac{1}{2} \\[8pt] 2u - 4 & \text{if }u \geq \dfrac{1}{2} \\ \end{array} \right. \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d9d3770bf7a14ef5fd79f3d81c5f9420_l3.png)
We have three points to help us graph ![]() :
: ![]() ,
, ![]() and
and ![]() . Unlike in the last two examples, these points do not give us information at the value
. Unlike in the last two examples, these points do not give us information at the value ![]() where the rule for
where the rule for ![]() changes. Substituting
changes. Substituting ![]() into the expression
into the expression ![]() gives
gives ![]() , so from
, so from ![]() ,
, ![]() , we get a hole at
, we get a hole at ![]() .
.
However, this hole is filled because ![]() and this produces the vertex at
and this produces the vertex at ![]() . The range of
. The range of ![]() is
is ![]() , with the minimum of
, with the minimum of ![]() being
being ![]() at
at ![]() . Moreover,
. Moreover, ![]() is decreasing on
is decreasing on ![]() and increasing on
and increasing on ![]() .
.
The graph of ![]() is given below.
is given below.
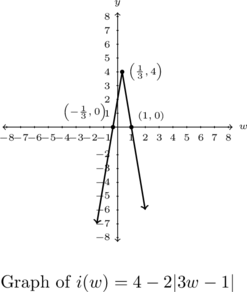
Example 1.4.1.4
For each of the functions below, analytically find the zeros of the function and the axis intercepts of the graph, if any exist. Rewrite the function using Definition 1.12 as a piecewise-defined function and sketch its graph. From the graph, determine the vertex, find the range of the function and any extrema, and then list the intervals over which the function is increasing, decreasing or constant.
![]()
Solution:
In what follows below, we will be doing quite a bit of substitution. As we have mentioned before, when substituting one expression in for another, the use of parentheses or other grouping symbols is highly recommended. Also, the dependent variable wasn’t specified so we use the default ![]() in each case.
in each case.
Analyze ![]() .
.
Solving ![]() yields
yields ![]() or
or ![]() . This gives two zeros,
. This gives two zeros, ![]() and
and ![]() , which correspond to two
, which correspond to two ![]() -intercepts,
-intercepts, ![]() and
and ![]() . Also,
. Also, ![]() , so the
, so the ![]() -intercept of the graph is
-intercept of the graph is ![]() . As in the previous example, the first step in rewriting
. As in the previous example, the first step in rewriting ![]() as a piecewise defined function is to rewrite
as a piecewise defined function is to rewrite ![]() as a piecewise function. Once again, we substitute the expression
as a piecewise function. Once again, we substitute the expression ![]() in for every occurrence of
in for every occurrence of ![]() in Definition 1.12:
in Definition 1.12:
![Rendered by QuickLaTeX.com \[ \begin{array}{ccc} |3w - 1| = \left\{ \begin{array}{rc} -(3w - 1) & \text{if } 3w - 1 < 0 \\ 3w - 1 & \text{if } 3w - 1 \geq 0 \\ \end{array} \right. & \longrightarrow & |3w - 1| = \left\{ \begin{array}{rc} -3w + 1 & \text{if } w < \dfrac{1}{3} \\[8pt] 3w - 1 & \text{if } w \geq \dfrac{1}{3} \\ \end{array} \right.\\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4a953f8d4d7a2e3d85facbc53edca5ce_l3.png)
Thus for ![]() ,
, ![]() , so
, so
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} i(w) &=& 4 - 2|3w - 1| \\ &=& 4 - 2(-3w + 1) \\ &=& 6w + 2. \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-8a33cbe45eff37b097f9b3b1479f9c3b_l3.png)
Likewise, for ![]() ,
, ![]() so
so
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} i(w) &=& 4 - 2|3w - 1| \\ &=& 4 - 2(3w - 1) \\ &=& -6w + 6. \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d3399663a3c73eaeede4c9c9e04873c1_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{array}{ccc} i(w) = 4 - 2 |3w - 1| = \left\{ \begin{array}{rc} 4 - 2(-3w + 1) & \text{if }w < \dfrac{1}{3} \\[8pt] 4 - 2(3w - 1) & \text{if }w \geq \dfrac{1}{3} \\ \end{array} \right. & \longrightarrow & i(w) = \left\{ \begin{array}{rc} 6w + 2 & \text{if } w < \dfrac{1}{3} \\[8pt] -6w + 6 & \text{if } w \geq \dfrac{1}{3} \\ \end{array} \right.\\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-889284c4603cbfa9e9ab1357e1064bb6_l3.png)
As with the previous example, we have three points on the graph of ![]() :
: ![]() ,
, ![]() and
and ![]() , but no information about happens at
, but no information about happens at ![]() . Substituting this value of
. Substituting this value of ![]() into the formula
into the formula ![]() would produce a hole at
would produce a hole at ![]() .
.
As we’ve seen several times already, however, ![]() so we don’t have a hole at
so we don’t have a hole at ![]() but, rather, the vertex. From the graph we see that the range of
but, rather, the vertex. From the graph we see that the range of ![]() is
is ![]() with the maximum of
with the maximum of ![]() being
being ![]() when
when ![]() . Also,
. Also, ![]() is increasing over
is increasing over ![]() and decreasing on
and decreasing on ![]() .
.
Its graph is given below.
As we take a step back and look at the graphs produced in Example 1.4.1, some patterns begin to emerge. Indeed, each of the graphs has the common `![]() ‘ shape (in the case of the function
‘ shape (in the case of the function ![]() it’s a `
it’s a `![]() ‘) with the vertex located at the
‘) with the vertex located at the ![]() -value where the rule for each function changes from one formula to the other. It turns out that, independent variable labels aside, each and every function in Example 1.4.1 can be rewritten in the form
-value where the rule for each function changes from one formula to the other. It turns out that, independent variable labels aside, each and every function in Example 1.4.1 can be rewritten in the form ![]() for real number parameters
for real number parameters ![]() ,
, ![]() and
and ![]() .
.
Each of the functions from Example 1.4.1 is rewritten in this form below and we record the vertex along with the slopes of the lines in the graph.
 :
:  ,
,  ,
, 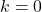 ; vertex
; vertex 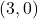 ; slopes
; slopes 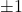
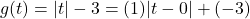 :
: 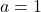 ,
, 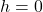 ,
, 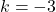 ; vertex
; vertex 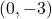 ; slopes
; slopes 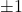
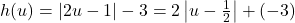 :
: 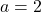 ,
, 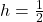 ,
, 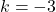 ; vertex
; vertex 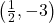 ; slopes
; slopes 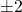
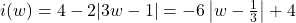 :
: 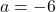 ,
, 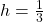 ,
, 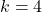 ; vertex
; vertex 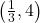 ; slopes
; slopes 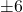
These specific examples suggest the following theorem.
Theorem 1.4
For real numbers ![]() ,
, ![]() and
and ![]() with
with ![]() , the graph of
, the graph of ![]() consists of parts of two lines with slopes
consists of parts of two lines with slopes ![]() which meet at a vertex
which meet at a vertex ![]() .
.
If ![]() , the shape resembles `
, the shape resembles `![]() ‘.
‘.
If ![]() , the shape resembles `
, the shape resembles `![]() ‘.
‘.
Moreover, the graph is symmetric about the line ![]() .
.
Proof: What separates Mathematics from the other sciences is its ability to actually prove patterns like the one stated in the theorem above as opposed to just verifying it by working more examples. The proof of Theorem 1.4 uses the exact same concepts as were used in Example 1.4.1, just in a more general context by which we mean using letters as parameters instead of numbers.
The first step is to rewrite ![]() as a piecewise function.
as a piecewise function.
![]()
We plug that work into ![]() to rewrite it as a piecewise function. For
to rewrite it as a piecewise function. For ![]() , we have
, we have ![]() , so
, so
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} F(x) &=& a|x - h| + k \\ &=& a(-x + h) + k \\ &=& -ax + ah + k \\ &=& -ax + (ah + k) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e15b8481dfc9259b1d491050778bfc28_l3.png)
Similarly, for ![]() , we have
, we have ![]() , so
, so
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl}F(x) &=& a|x - h| + k \\ &=& a(x - h) + k \\ &=& ax - ah + k \\ &=& ax + (-ah + k) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e8e5325ee6fbfdf61b57f65ee1304cdd_l3.png)
Hence,
![]()
All three parameters, ![]() ,
, ![]() and
and ![]() , are fixed (but arbitrary) real numbers. Thus, for any given choice of
, are fixed (but arbitrary) real numbers. Thus, for any given choice of ![]() ,
, ![]() and
and ![]() the numbers
the numbers ![]() and
and ![]() are also just numbers as opposed to variables. This shows that the graph of
are also just numbers as opposed to variables. This shows that the graph of ![]() is comprised of pieces of two lines,
is comprised of pieces of two lines, ![]() and
and ![]() , the former with slope
, the former with slope ![]() and the latter with slope
and the latter with slope ![]() . Note that substituting
. Note that substituting ![]() into
into ![]() produces
produces ![]() and substituting
and substituting ![]() into
into ![]() also produces
also produces ![]() . This tells us that the two linear pieces meet at the point
. This tells us that the two linear pieces meet at the point ![]()
If ![]() then
then ![]() so the line
so the line ![]() , hence
, hence ![]() , is decreasing on
, is decreasing on ![]() .
.
Similarly, the line ![]() , hence
, hence ![]() , is increasing on
, is increasing on ![]() .
.
This produces a `![]() ‘ shape. On the other hand, if
‘ shape. On the other hand, if ![]() then
then ![]() which produces a `
which produces a `![]() ‘ shape because
‘ shape because ![]() is increasing on
is increasing on ![]() followed by decreasing on
followed by decreasing on ![]() . (Said another way,
. (Said another way, ![]() means that the first linear piece has a positive slope and
means that the first linear piece has a positive slope and ![]() means that the second piece has a negative slope.)
means that the second piece has a negative slope.)
To show that the graph is symmetric about the line ![]() , we need to show that if we move left or right the same distance away from
, we need to show that if we move left or right the same distance away from ![]() , then we get the same
, then we get the same ![]() -value on the graph. Suppose we move
-value on the graph. Suppose we move ![]() to the right or left of
to the right or left of ![]() . The
. The ![]() -values are the function values so we need to show that
-values are the function values so we need to show that ![]() . Given that
. Given that
![]()
and
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} F(a - \Delta x) &=& a | a - \Delta x - a| + k\\ &=& a|-\Delta x| + k \\ &=& a|\Delta x| + k \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-088a289334bb730c67bbdea588b63863_l3.png)
we see that ![]() . Thus we have shown that the
. Thus we have shown that the ![]() -values on the graph on either side of
-values on the graph on either side of ![]() are equal provided we move the same distance away from
are equal provided we move the same distance away from ![]() . This completes the proof.
. This completes the proof. ![]()
The line ![]() in Theorem 1.4 is called the axis of symmetry of the graph of
in Theorem 1.4 is called the axis of symmetry of the graph of ![]() . This language is consistent with the basics of symmetry discussed in Section 1.1 and we will build upon our work here in several upcoming sections. For now, we simply present two graphs illustrating the concept of the axis of symmetry below.
. This language is consistent with the basics of symmetry discussed in Section 1.1 and we will build upon our work here in several upcoming sections. For now, we simply present two graphs illustrating the concept of the axis of symmetry below.

While Theorem 1.4 and its proof are specific to the particular family of absolute value functions, there are ideas here that apply to all functions. Thus we wish to take a slight detour away from the main narrative to argue this result again from an even more generalized viewpoint. Our goal is to `build’ the formula ![]() from
from ![]() in three stages, each corresponding to the role of one of the parameters
in three stages, each corresponding to the role of one of the parameters ![]() ,
, ![]() and
and ![]() , and track the geometric changes that go along with each stage. We will revisit all of the ideas described below in complete generality in Section 1.6.
, and track the geometric changes that go along with each stage. We will revisit all of the ideas described below in complete generality in Section 1.6.
The graph of ![]() consists of the points
consists of the points ![]() .[3] Consider
.[3] Consider ![]() . The graph of
. The graph of ![]() is the set of points
is the set of points ![]() . If we relabel
. If we relabel ![]() , then
, then ![]() , and as
, and as ![]() varies through all of the real numbers, so does
varies through all of the real numbers, so does ![]() and vice-versa.[4]
and vice-versa.[4]
Hence, we can write ![]() . If we fix a
. If we fix a ![]() -coordinate,
-coordinate, ![]() , we see that the corresponding points on the graph of
, we see that the corresponding points on the graph of ![]() and
and ![]() ,
, ![]() and
and ![]() , respectively, differ only in that one is horizontally shifted by
, respectively, differ only in that one is horizontally shifted by ![]() . In other words, to get the graph of
. In other words, to get the graph of ![]() , we simply take the graph of
, we simply take the graph of ![]() and shift each point horizontally by adding
and shift each point horizontally by adding ![]() to the
to the ![]() -coordinate. Translating the graph in this manner preserves the `
-coordinate. Translating the graph in this manner preserves the `![]() ‘ shape and symmetry, but moves the vertex from
‘ shape and symmetry, but moves the vertex from ![]() to
to ![]() .
.
Next, we examine ![]() and compare its graph to that of
and compare its graph to that of ![]() . The graph of
. The graph of ![]() consists of the points
consists of the points ![]() whereas the graph of
whereas the graph of ![]() consists of the points
consists of the points ![]() . The only difference between the points
. The only difference between the points ![]() and
and ![]() is that the
is that the ![]() -coordinate of one is
-coordinate of one is ![]() times the
times the ![]() -coordinate of the other. If
-coordinate of the other. If ![]() , all we are doing is scaling the
, all we are doing is scaling the ![]() -axis by a factor of
-axis by a factor of ![]() . As we’ve seen when plotting points and graphing functions, the scaling of the
. As we’ve seen when plotting points and graphing functions, the scaling of the ![]() -axis affects only the relative vertical displacement of points[5] and not the overall shape.
-axis affects only the relative vertical displacement of points[5] and not the overall shape.
If ![]() , then in addition to scaling the vertical axis, we are reflecting the points across the
, then in addition to scaling the vertical axis, we are reflecting the points across the ![]() -axis.[6] Such a transformation doesn’t change the `
-axis.[6] Such a transformation doesn’t change the `![]() ‘ shape except for flipping it upside-down to make it a `
‘ shape except for flipping it upside-down to make it a `![]() ‘. In either case, the vertex
‘. In either case, the vertex ![]() stays put at
stays put at ![]() because the
because the ![]() -value of the vertex is
-value of the vertex is ![]() and
and ![]() regardless if
regardless if ![]() or
or ![]() .
.
Last, we examine the graph of ![]() to see how it relates to the graph of
to see how it relates to the graph of ![]() . The graph of
. The graph of ![]() consists of the points
consists of the points ![]() whereas the graph of
whereas the graph of ![]() consists of the points
consists of the points ![]() . The difference between the corresponding points
. The difference between the corresponding points ![]() and
and ![]() is the addition of
is the addition of ![]() in the
in the ![]() -coordinate of the latter. Adding
-coordinate of the latter. Adding ![]() to each of the
to each of the ![]() -values translates the graph of
-values translates the graph of ![]() vertically by
vertically by ![]() units. The basic shape doesn’t change but the vertex goes from
units. The basic shape doesn’t change but the vertex goes from ![]() to
to ![]() .
.
In summary, the graph of ![]() can be obtained from the graph of
can be obtained from the graph of ![]() in three steps: first, add
in three steps: first, add ![]() to each of the
to each of the ![]() -coordinates; second, multiply each
-coordinates; second, multiply each ![]() -coordinate by
-coordinate by ![]() ; and third, add
; and third, add ![]() to each
to each ![]() -coordinate. Geometrically, these steps mean that we first move the graph left or right, then scale the
-coordinate. Geometrically, these steps mean that we first move the graph left or right, then scale the ![]() -axis by a factor of
-axis by a factor of ![]() (and reflect across the
(and reflect across the ![]() -axis if
-axis if ![]() ), and then move the graph up or down. Throughout all of these transformations, the graph maintains its `
), and then move the graph up or down. Throughout all of these transformations, the graph maintains its `![]() ‘ or `
‘ or `![]() ‘ shape.
‘ shape.
Of course, not every function involving absolute values can be written in the form given in Theorem 1.4. A good example of this is ![]() . However recognizing the ones that can be rewritten will greatly simplify the graphing process. In the next example, we graph four more absolute value functions, two using Theorem 1.4 and two using Definition 1.12.
. However recognizing the ones that can be rewritten will greatly simplify the graphing process. In the next example, we graph four more absolute value functions, two using Theorem 1.4 and two using Definition 1.12.
Example 1.4.2
Example 1.4.2.1a
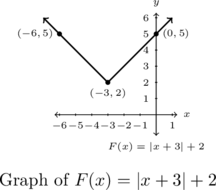
Graph each of the functions below using Theorem 1.4 or by rewriting it as a piecewise defined function using Definition 1.12. Find the zeros, axis-intercepts and the extrema (if any exist) and then list the intervals over which the function is increasing, decreasing or constant.
![]()
Solution:
Graph and analyze ![]() .
.
Rewriting ![]() , we have
, we have ![]() in the form stated in Theorem 1.4 with
in the form stated in Theorem 1.4 with ![]() ,
, ![]() and
and ![]() .
.
The vertex is ![]() and the graph will be a `
and the graph will be a `![]() ‘ shape.
‘ shape.
Seeing as the vertex is already above the ![]() -axis and the graph opens upwards, there are no
-axis and the graph opens upwards, there are no ![]() -intercepts on the graph of
-intercepts on the graph of ![]() , hence there are no zeros.[7]
, hence there are no zeros.[7]
With ![]() , the
, the ![]() -intercept is
-intercept is ![]() .
.
To get a third point, we can pick an arbitrary ![]() -value to the left of the vertex or we could use symmetry: three units to the right of the vertex the
-value to the left of the vertex or we could use symmetry: three units to the right of the vertex the ![]() -value is
-value is ![]() , so the same must be true three units to the left of the vertex, at
, so the same must be true three units to the left of the vertex, at ![]() . Sure enough,
. Sure enough, ![]() .
.
The range of ![]() is
is ![]() with its minimum of
with its minimum of ![]() when
when ![]() and
and ![]() decreasing on
decreasing on ![]() then increasing on
then increasing on ![]() .
.
The graph is below.
Example 1.4.2.1b
Graph each of the functions below using Theorem 1.4 or by rewriting it as a piecewise defined function using Definition 1.12. Find the zeros, axis-intercepts and the extrema (if any exist) and then list the intervals over which the function is increasing, decreasing or constant.
![]()
Solution:
Graph and analyze ![]() .
.
We see in the formula for ![]() that
that ![]() appears only once to the first power inside the absolute values, so we proceed to rewrite it in the form
appears only once to the first power inside the absolute values, so we proceed to rewrite it in the form ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f(t) & =& \dfrac{4 - |5-3t|}{2} \\ [10pt] & = & - \dfrac{|5-3t|}{2} + \dfrac{4}{2} \\ [12pt] & = & \left(-\dfrac{1}{2}\right) \left| (-3) \left( t - \dfrac{5}{3} \right) \right| + 2 \\ [12pt] & = & \left(-\dfrac{1}{2}\right) |-3| \left| t - \dfrac{5}{3} \right| + 2 \\ [12pt] & = & -\dfrac{3}{2} \left| t - \dfrac{5}{3} \right| + 2. \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-aa8ad23617ff744eb65f538529a2f9b1_l3.png)
Matching up the constants in the formula ![]() to the parameters of
to the parameters of ![]() in Theorem 1.4, we identify
in Theorem 1.4, we identify ![]() ,
, ![]() and
and ![]() .
.
Hence the vertex is ![]() , and the graph is shaped like `
, and the graph is shaped like `![]() ‘ comprised of pieces of lines with slopes
‘ comprised of pieces of lines with slopes ![]() .
.
To find the zeros of ![]() , we set
, we set ![]() . (We can use either expression here.) Solving
. (We can use either expression here.) Solving ![]() , we get
, we get ![]() , so
, so ![]() . Hence our zeros are
. Hence our zeros are ![]() and
and ![]() , producing the
, producing the ![]() -intercepts
-intercepts ![]() and
and ![]() .
.
Using either formula gives ![]() , so our
, so our ![]() -intercept is
-intercept is ![]() .
.
Plotting the vertex, along with the intercepts, gives us enough information to produce the graph below.
The range is ![]() with a maximum of
with a maximum of ![]() at
at ![]() and
and ![]() is increasing on
is increasing on ![]() then decreasing on
then decreasing on ![]() .
.
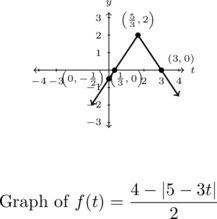
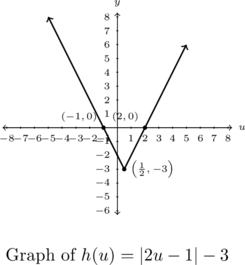
Example 1.4.2.1c
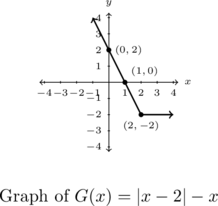
Graph each of the functions below using Theorem 1.4 or by rewriting it as a piecewise defined function using Definition 1.12. Find the zeros, axis-intercepts and the extrema (if any exist) and then list the intervals over which the function is increasing, decreasing or constant.
![]()
Solution:
Graph and analyze ![]() .
.
We are unable to apply Theorem 1.4 to ![]() because there is an
because there is an ![]() both inside and outside of the absolute value. We can, however, rewrite the function as a piecewise function using Definition 1.12. Our first step is to rewrite
both inside and outside of the absolute value. We can, however, rewrite the function as a piecewise function using Definition 1.12. Our first step is to rewrite ![]() as a piecewise function:
as a piecewise function:
![]()
Hence, for ![]() ,
, ![]() so
so ![]() . Likewise, for
. Likewise, for ![]() ,
, ![]() so
so ![]() .
.
![]()
To find the zeros of ![]() , we set
, we set ![]() . Solving
. Solving ![]() can be problematic, given that
can be problematic, given that ![]() is both inside and outside of the absolute values.[8] We can, however, use the piecewise description of
is both inside and outside of the absolute values.[8] We can, however, use the piecewise description of ![]() . With
. With ![]() for
for ![]() , we solve
, we solve ![]() to get
to get ![]() . This works because
. This works because ![]() , so we have
, so we have ![]() as the zero of
as the zero of ![]() corresponding to the
corresponding to the ![]() -intercept
-intercept ![]() . The other piece of
. The other piece of ![]() is
is ![]() which is never
which is never ![]() . For the
. For the ![]() -intercept, we find
-intercept, we find ![]() , and get
, and get ![]() .
.
To graph ![]() , we have the line
, we have the line ![]() which contains
which contains ![]() and
and ![]() and continues to a hole at
and continues to a hole at ![]() . At this point,
. At this point, ![]() takes over and we have a horizontal line containing
takes over and we have a horizontal line containing ![]() extending indefinitely to the right.
extending indefinitely to the right.
The range of ![]() is
is ![]() with a minimum value of
with a minimum value of ![]() attained for all
attained for all ![]() . Moreover,
. Moreover, ![]() is decreasing on
is decreasing on ![]() and then constant on
and then constant on ![]() .
.
The graph is below.
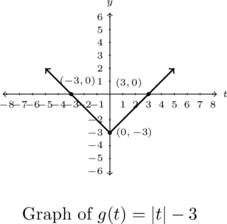
Example 1.4.2.1d
Graph each of the functions below using Theorem 1.4 or by rewriting it as a piecewise defined function using Definition 1.12. Find the zeros, axis-intercepts and the extrema (if any exist) and then list the intervals over which the function is increasing, decreasing or constant.
![]()
Solution:
Graph and analyze ![]() .
.
Once again we are unable to use Theorem 1.4 because ![]() has two absolute values with no apparent way to combine them. Thus we proceed by re-writing the function
has two absolute values with no apparent way to combine them. Thus we proceed by re-writing the function ![]() with two separate applications of Definition 1.12 to remove each instance of the absolute values. To start with we have:
with two separate applications of Definition 1.12 to remove each instance of the absolute values. To start with we have:
![]()
Taken together, these break the domain into three pieces: ![]() ,
, ![]() and
and ![]() .
.
For ![]() ,
, ![]() and
and ![]() . Therefore
. Therefore
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(t) &=& |t - 2| - |t| \\ &=& (-t + 2) - (-t) \\ &=& 2 \text{ for } t < 0. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-ea0e10956e761c05efad07fe56336a2d_l3.png)
For ![]() ,
, ![]() and
and ![]() , so
, so
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(t) &=& |t-2| - |t| \\ &=& (-t+2) - (t) \\ &=& -2t + 2. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a75862b18aae5d5d97ac23b76f43e2e9_l3.png)
Last, for ![]() ,
, ![]() and
and ![]() , so
, so
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(t) &=& |t-2| - |t|\\ &=& (t - 2) - (t) \\ &=& -2. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-02007aa409c308dca0c67bcbb00bd951_l3.png)
Putting all three parts together yields:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(t) &=& |t - 2| - |t| \\[8pt] &=& \left\{ \begin{array}{rc} (-t + 2) - (-t) & \text{if } t < 0 \\ (-t + 2) - (t) & \text{if } 0 \leq t < 2 \\ (t - 2) - (t) & \text{if } t \geq 2 \end{array} \right.\\[8pt] &=& \left\{ \begin{array}{rc} 2 & \text{if } t < 0 \\ -2t + 2 & \text{if } 0 \leq t < 2 \\ -2 & \text{if } t \geq 2 \end{array} \right. \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-574e6c8e9db36806ae6edd65ec6efe0c_l3.png)
As with the previous example, we’ll delay discussing the absolute value algebra needed to find the zeros of ![]() and use the piecewise description instead.
and use the piecewise description instead.
To graph ![]() , we have the horizontal line
, we have the horizontal line ![]() up to, but not including, the point
up to, but not including, the point ![]() .
.
For ![]() , we have the line
, we have the line ![]() which has a
which has a ![]() -intercept at
-intercept at ![]() (thus picking up where the first part left off) and a
(thus picking up where the first part left off) and a ![]() -intercept at
-intercept at ![]() . This piece ends with a hole at
. This piece ends with a hole at ![]() which is promptly plugged by the horizontal line
which is promptly plugged by the horizontal line ![]() for
for ![]() .
.
Hence the only zero of ![]() is
is ![]() .
.
The range of ![]() is
is ![]() with a minimum of
with a minimum of ![]() achieved for all
achieved for all ![]() , and a maximum of
, and a maximum of ![]() for
for ![]() . We note that
. We note that ![]() is constant on
is constant on ![]() and
and ![]() , but with different values, and
, but with different values, and ![]() is decreasing on
is decreasing on ![]() .
.
The graph is given below.
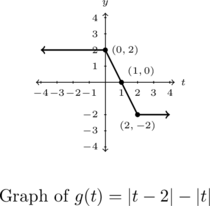
Example 1.4.2.2
Use Theorem 1.4 to write a possible formula for ![]() whose graph is given below:
whose graph is given below:
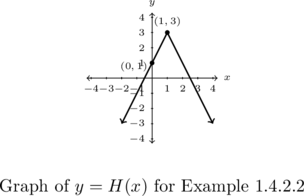
Solution:
Write a formula for ![]() given the graph below.
given the graph below.

We are told to use Theorem 1.4 to find a formula for ![]() so we start with
so we start with ![]() and look for real numbers
and look for real numbers ![]() ,
, ![]() and
and ![]() that make sense.
that make sense.
The vertex is labeled as ![]() , meaning
, meaning ![]() and
and ![]() .
.
Hence we know ![]() , so all that is left for us to find is the value of
, so all that is left for us to find is the value of ![]() . The only other point labeled for us is
. The only other point labeled for us is ![]() , meaning
, meaning ![]() . Substituting
. Substituting ![]() into our formula for
into our formula for ![]() gives:
gives:
![]()
Given that ![]() , we have
, we have ![]() , so
, so ![]() .
.
Our final answer is ![]() .
.
If nothing else, Example 1.4.2 demonstrates the value of changing forms of functions and the utility of the interplay between algebraic and graphical descriptions of functions. These themes resonate time and time again in this and later courses in Mathematics.
To that end, let’s call ![]() and
and ![]() . If we graph
. If we graph ![]() and
and ![]() on the same set of axes then, by looking for
on the same set of axes then, by looking for ![]() values where
values where ![]() we are looking for
we are looking for ![]() -values which have the same
-values which have the same ![]() -value on both graphs. That is, the solutions to
-value on both graphs. That is, the solutions to ![]() are the
are the ![]() -coordinates of the intersection points of the two graphs. We graph
-coordinates of the intersection points of the two graphs. We graph ![]() (the characteristic `
(the characteristic `![]() ‘) along with
‘) along with ![]() (the horizontal line) below on the far left. Indeed, the two graphs intersect at
(the horizontal line) below on the far left. Indeed, the two graphs intersect at ![]() and
and ![]() so our solutions to
so our solutions to ![]() are the
are the ![]() -values of these points,
-values of these points, ![]() .
.

Likewise, if we wish to solve ![]() , we can view this as a functional inequality
, we can view this as a functional inequality ![]() which means we are looking for the
which means we are looking for the ![]() -values where the
-values where the ![]() values are less than the corresponding
values are less than the corresponding ![]() values. On the graphs, this means we’d be looking for the
values. On the graphs, this means we’d be looking for the ![]() -values where the
-values where the ![]() -values of
-values of ![]() are less than, hence below, those on the graph of
are less than, hence below, those on the graph of ![]() . In the middle picture above we see that the graph of
. In the middle picture above we see that the graph of ![]() is below the graph of
is below the graph of ![]() between
between ![]() and
and ![]() , so our solution is
, so our solution is ![]() , or in interval notation,
, or in interval notation, ![]() .
.
Finally, the inequality ![]() is equivalent to
is equivalent to ![]() so we are looking for the
so we are looking for the ![]() -values where the graph of
-values where the graph of ![]() is above the graph of
is above the graph of ![]() .[9] The picture on the far right above shows that this is true for all
.[9] The picture on the far right above shows that this is true for all ![]() or for all
or for all ![]() . In interval notation, the solution set is
. In interval notation, the solution set is ![]() .
.
The methodology and reasoning behind solving the above equation and inequalities extend to any pair of functions ![]() and
and ![]() , because when graphed on the same set of axes, function outputs are always the dependent variable or the ordinate (second coordinate) of the ordered pairs which comprise the graph. In general:
, because when graphed on the same set of axes, function outputs are always the dependent variable or the ordinate (second coordinate) of the ordered pairs which comprise the graph. In general:
Graphical Interpretation of Equations and Inequalities
Suppose ![]() and
and ![]() are functions whose domains and ranges are sets of real numbers.
are functions whose domains and ranges are sets of real numbers.
- The solutions to
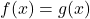 are the
are the  -values where the graphs of
-values where the graphs of  and
and  intersect.
intersect. - The solution to
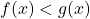 is the set of
is the set of  -values where the graph of
-values where the graph of  is below the graph of
is below the graph of  .
. - The solution to
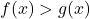 is the set of
is the set of  -values where the graph of
-values where the graph of  above the graph of
above the graph of  .
.
Let’s return to Example 1.4.2 where we were asked to find the zeros of the functions ![]() and
and ![]() . In that Example, instead of tackling the algebra involving the absolute values head on we rewrote each function as a piecewise-defined function and obtained our solutions that way.
. In that Example, instead of tackling the algebra involving the absolute values head on we rewrote each function as a piecewise-defined function and obtained our solutions that way.
Let’s see what this looks like graphically. Note that solving ![]() is equivalent to solving
is equivalent to solving ![]() . We graphed
. We graphed ![]() and
and ![]() on the same set of axes on the left of the top of the next page and it appears as if we have just one point of intersection, corresponding to just one solution.
on the same set of axes on the left of the top of the next page and it appears as if we have just one point of intersection, corresponding to just one solution.
Indeed, we can show that there is just one point of intersection. The graph of ![]() is comprised of parts of two lines,
is comprised of parts of two lines, ![]() and
and ![]() . The first line has a slope of
. The first line has a slope of ![]() and the second has slope
and the second has slope ![]() . The line
. The line ![]() also has a slope
also has a slope ![]() meaning it and the `right half’ of
meaning it and the `right half’ of ![]() are parallel, so they never intersect. If our graphs are accurate enough, we may even be able to guess that the solution is
are parallel, so they never intersect. If our graphs are accurate enough, we may even be able to guess that the solution is ![]() , which we can verify by substituting
, which we can verify by substituting ![]() into
into ![]() and seeing that it checks.
and seeing that it checks.
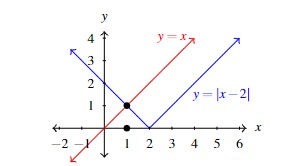
Likewise, solving ![]() is equivalent to solving
is equivalent to solving ![]() . We graphed
. We graphed ![]() and
and ![]() and used the same arguments to get the solution
and used the same arguments to get the solution ![]() here as well.
here as well.
There is more to see here. Consider solving ![]() algebraically using the techniques from a previous Algebra course (or Section 0.6.2). Our first step would be to isolate the absolute value quantity:
algebraically using the techniques from a previous Algebra course (or Section 0.6.2). Our first step would be to isolate the absolute value quantity: ![]() . We then `drop’ the absolute value by paying the price of a `
. We then `drop’ the absolute value by paying the price of a `![]() ‘:
‘: ![]() . This gives us two equations:
. This gives us two equations: ![]() and
and ![]() . The first equation,
. The first equation, ![]() reduces to
reduces to ![]() which has no solution. The second equation,
which has no solution. The second equation, ![]() , does have a solution, namely
, does have a solution, namely ![]() .
.
How does the algebra tie into the graphs above? Instead of `dropping’ the absolute value and tagging the right hand side with a ![]() , we can think about the piecewise definition of
, we can think about the piecewise definition of ![]() and write
and write ![]() depending on if
depending on if ![]() or if
or if ![]() . That is,
. That is, ![]() is more precisely equivalent to the two equations:
is more precisely equivalent to the two equations: ![]() which is valid for
which is valid for ![]() or
or ![]() which is valid for
which is valid for ![]() .
.
Graphically, the first equation is looking for intersection points between the `left half’ of the `![]() ‘ of
‘ of ![]() and the line
and the line ![]() . Indeed,
. Indeed, ![]() is equivalent to
is equivalent to ![]() from which we obtain our solution
from which we obtain our solution ![]() . Likewise, the second equation,
. Likewise, the second equation, ![]() is looking for intersection points of the `right half’ of the `
is looking for intersection points of the `right half’ of the `![]() ‘ and the line
‘ and the line ![]() , but there is none. The equation
, but there is none. The equation ![]() is telling us that for us to have any solutions, the lines
is telling us that for us to have any solutions, the lines ![]() and
and ![]() , which have the same slope, must also have the same
, which have the same slope, must also have the same ![]() -intercepts: that is,
-intercepts: that is, ![]() would have to equal
would have to equal ![]() and that’s just silly.
and that’s just silly.
Similarly, when solving ![]() or
or ![]() , we can use our graphs to prove that the only intersection point is when the `left half’ of
, we can use our graphs to prove that the only intersection point is when the `left half’ of ![]() intersects the `right half’ of
intersects the `right half’ of ![]() – that is, when
– that is, when ![]() . The moral of the story is this: careful graphs can help us simplify the algebra, because we can narrow down the cases. This is especially useful in solving inequalities, as we’ll see in our next example.
. The moral of the story is this: careful graphs can help us simplify the algebra, because we can narrow down the cases. This is especially useful in solving inequalities, as we’ll see in our next example.
Example 1.4.3
Example 1.4.3.1
Solve the following equations and inequalities.
![]()
Solution:
Solve ![]() for
for ![]() .
.
We begin by graphing ![]() and
and ![]() to look for intersection points. Using Theorem 1.4, we know that the graph of
to look for intersection points. Using Theorem 1.4, we know that the graph of ![]() has a vertex at
has a vertex at ![]() and is a `
and is a `![]() ‘ shape, so there are
‘ shape, so there are ![]() -intercepts to find. Solving
-intercepts to find. Solving ![]() , we get
, we get ![]() , or
, or ![]() . Hence, we have two
. Hence, we have two ![]() -intercepts:
-intercepts: ![]() and
and ![]() .
.
We know from Section 1.3.1 that the graph of ![]() is a line with slope
is a line with slope ![]() and
and ![]() -intercept
-intercept ![]() . To find the
. To find the ![]() -intercept here we solve
-intercept here we solve ![]() and get
and get ![]() .
.
Hence, ![]() is an
is an ![]() -intercept here as well, and we have stumbled upon one solution to
-intercept here as well, and we have stumbled upon one solution to ![]() , namely
, namely ![]() .
.
The question is if there are any other solutions. Our graph (below on the left) certainly looks as if there is just one intersection point, but we know from Theorem 1.4 that the slopes of the linear parts of ![]() are
are ![]() . The slope of
. The slope of ![]() is
is ![]() and
and ![]() so we know that the left hand side of the`
so we know that the left hand side of the`![]() ‘ must meet up with the graph of the line because they are not parallel.[10]
‘ must meet up with the graph of the line because they are not parallel.[10]
Definition 1.12 tells us that when ![]() ,
, ![]() , so
, so ![]() . Hence we set about solving
. Hence we set about solving ![]() and get
and get ![]() .
.
Both ![]() and
and ![]() check in our original equation,
check in our original equation, ![]() , so we have found our two solutions.[11]
, so we have found our two solutions.[11]
Example 1.4.3.2
Solve the following equations and inequalities.
![]()
Solution:
Solve ![]() for
for ![]() .
.
While we could graph ![]() and
and ![]() to help us find solutions, we choose to rewrite the equation as
to help us find solutions, we choose to rewrite the equation as ![]() . This way, we have somewhat easier graphs to deal with, namely
. This way, we have somewhat easier graphs to deal with, namely ![]() and
and ![]() . The first graph,
. The first graph, ![]() , has a vertex at
, has a vertex at ![]() and is shaped like a `
and is shaped like a `![]() ‘ with slopes
‘ with slopes ![]() and a
and a ![]() -intercept of
-intercept of ![]() .
.
The second graph, ![]() , has a vertex at
, has a vertex at ![]() and is also shaped like a `
and is also shaped like a `![]() ,’ with slopes
,’ with slopes ![]() , and has no
, and has no ![]() -intercepts.
-intercepts.
To our surprise and delight, the graphs appear to overlap for ![]() . Indeed, for
. Indeed, for ![]() ,
, ![]() and
and ![]() .
.
Due to the fact that the formulas are identical for these values of ![]() , our solutions are all values of
, our solutions are all values of ![]() with
with ![]() . Using interval notation, we state our solution as
. Using interval notation, we state our solution as ![]() . (The other parts of the graphs are non-intersecting parallel lines so we ignored them.)
. (The other parts of the graphs are non-intersecting parallel lines so we ignored them.)
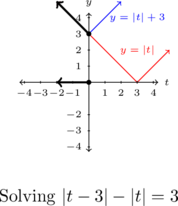
Example 1.4.3.3
Solve the following equations and inequalities.
![]()
Solution:
Solve ![]() for
for ![]() .
.
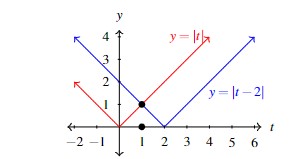
To solve ![]() , we first graph
, we first graph ![]() and
and ![]() . The former is `
. The former is `![]() ‘ shaped with a vertex at
‘ shaped with a vertex at ![]() and a
and a ![]() -intercept of
-intercept of ![]() .
.
The latter is a line with ![]() -intercept
-intercept ![]() , slope
, slope ![]() and
and ![]() -intercept
-intercept ![]() .
.
The picture shows two intersection points. To find these, we solve the equations: ![]() , obtaining
, obtaining ![]() , and
, and ![]() obtaining
obtaining ![]() .
.
Graphically, the inequality ![]() is looking for where the graph of
is looking for where the graph of ![]() , the `
, the `![]() ,’ intersects (
,’ intersects (![]() ) or is above (
) or is above (![]() ) the line
) the line ![]() . The graph shows this happening whenever
. The graph shows this happening whenever ![]() or
or ![]() . Using interval notation, our solution is
. Using interval notation, our solution is ![]() .
.
While we cannot check every single ![]() value individually, choosing test values
value individually, choosing test values ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() to see if the original inequality
to see if the original inequality ![]() holds would help us verify our solution.
holds would help us verify our solution.

Example 1.4.3.4
Solve the following equations and inequalities.
![]()
Solution:
Solve ![]() for
for ![]() .
.
Recall that the inequality ![]() is an example of a `compound’ inequality in that is two inequalities in one.[12] The values of
is an example of a `compound’ inequality in that is two inequalities in one.[12] The values of ![]() in the solution set need to satisfy
in the solution set need to satisfy ![]() and
and ![]() .
.
To help us sort through the cases, we graph the horizontal lines ![]() and
and ![]() along with the `
along with the `![]() ‘ shaped
‘ shaped ![]() with vertex
with vertex ![]() and
and ![]() -intercept
-intercept ![]() .
.
Geometrically, we are looking for where ![]() is strictly above the line
is strictly above the line ![]() but below (or meets) the line
but below (or meets) the line ![]() . Solving
. Solving ![]() gives
gives ![]() and
and ![]() whereas solving
whereas solving ![]() gives
gives ![]() or
or ![]() . Per the graph, we see that
. Per the graph, we see that ![]() lies between
lies between ![]() and
and ![]() when
when ![]() and again when
and again when ![]() .
.
In interval notation, our solution is ![]() .
.
As with the previous example, it is impossible to check each and every one of these solutions, but choosing ![]() values both in and around the solution intervals would give us some numerical confidence we have the correct and complete solution.
values both in and around the solution intervals would give us some numerical confidence we have the correct and complete solution.
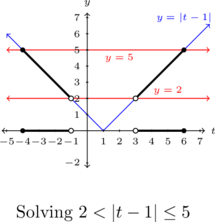
We will see the interplay of Algebra and Geometry throughout the rest of this course. In the Exercises, do not hesitate to use whatever mix of algebraic and graphical methods you deem necessary to solve the given equation or inequality. Indeed, there is great value in checking your algebraic answers graphically and vice-versa.
One of the classic applications of inequalities involving absolute values is the notion of tolerances.[13] Recall that for real numbers ![]() and
and ![]() , the quantity
, the quantity ![]() may be interpreted as the distance from
may be interpreted as the distance from ![]() to
to ![]() . Solving inequalities of the form
. Solving inequalities of the form ![]() for
for ![]() can then be interpreted as finding all numbers
can then be interpreted as finding all numbers ![]() which lie within
which lie within ![]() units of
units of ![]() . We can think of the number
. We can think of the number ![]() as a `tolerance’ and our solutions
as a `tolerance’ and our solutions ![]() as being within an accepted tolerance of
as being within an accepted tolerance of ![]() . We use this principle in the next example.
. We use this principle in the next example.
Example 1.4.4
Example 1.4.4
Suppose a manufacturer needs to produce a ![]() inch by
inch by ![]() inch square piece of particle board as part of a home office desk kit. How close does the side of the piece of particle board need to be cut to
inch square piece of particle board as part of a home office desk kit. How close does the side of the piece of particle board need to be cut to ![]() inches to guarantee that the area of the piece is within a tolerance of
inches to guarantee that the area of the piece is within a tolerance of ![]() square inches of the target area of
square inches of the target area of ![]() square inches?
square inches?
Solution:
Let ![]() denote the length of the side of the square piece of particle board so that the area of the board is
denote the length of the side of the square piece of particle board so that the area of the board is ![]() square inches. Our tolerance specifies that the area of the board,
square inches. Our tolerance specifies that the area of the board, ![]() , needs to be within
, needs to be within ![]() square inches of
square inches of ![]() . Mathematically, this translates to
. Mathematically, this translates to ![]() .
.
Rewriting, we get ![]() , or
, or ![]() . At this point, we take advantage of the fact that the square root is increasing.[14] Therefore, taking square roots preserves the inequality. When simplifying, we keep in mind that
. At this point, we take advantage of the fact that the square root is increasing.[14] Therefore, taking square roots preserves the inequality. When simplifying, we keep in mind that ![]() represents a length and thus
represents a length and thus ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 575.75 \leq & x^2 & \leq 576.25 & \\ \sqrt{575.75} \leq & \sqrt{x^2} & \leq \sqrt{576.25} & \text{(take square roots.)} \\ \sqrt{575.75} \leq & |x| & \leq \sqrt{576.25} & \text{($\sqrt{x^2} = |x|$)} \\ \sqrt{575.75} \leq & x & \leq \sqrt{576.25} & \text{($|x| = x$ as $x>0$)} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f9524e07c45a7f156a431b1d1a8b6cb7_l3.png)
The side of the piece of particle board must be between ![]() and
and ![]() inches. This results in a tolerance of (approximately)
inches. This results in a tolerance of (approximately) ![]() inches of the target length of
inches of the target length of ![]() inches, to ensure that the area is within
inches, to ensure that the area is within ![]() square inches of
square inches of ![]() .
.
1.4.3 Section Exercises
In Exercises 1 – 6, graph the function using Theorem 1.4. Find the axis intercepts of each graph, if any exist. From the graph, determine the domain and range of each function, the maximum and minimum of each function, if they exist, and list the intervals on which the function is increasing, decreasing or constant.
In Exercises 7 – 10, find a formula for each function below in the form ![]() .
.
-
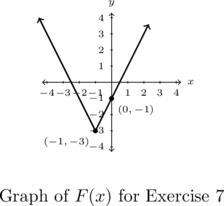
-
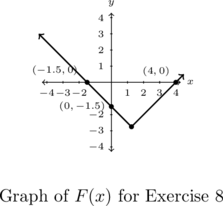
-
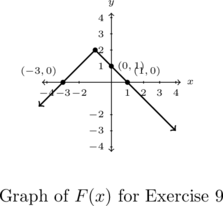
-
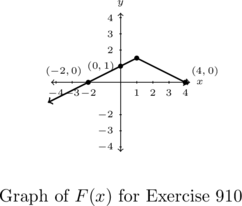
- Graph the following pairs of functions on the same set of axes:
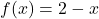 and
and 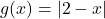
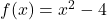 and
and 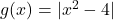
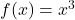 and
and 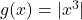
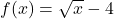 and
and 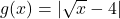
Choose more functions
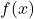 and graph
and graph 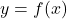 alongside
alongside 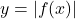 until you can explain how, in general, one would obtain the graph of
until you can explain how, in general, one would obtain the graph of 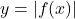 given the graph of
given the graph of 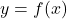 . How does your explanation tie in with with Definition 1.12?
. How does your explanation tie in with with Definition 1.12? - Explain the function below cannot be written in the form
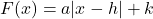 . Write
. Write 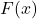 as a piecewise-defined linear function.
as a piecewise-defined linear function.
In Exercises 13 – 18, graph the function by rewriting each function as a piecewise defined function using Definition 1.12. Find the axis intercepts of each graph, if any exist. From the graph, determine the domain and range of each function, the maximum and minimum of each function, if they exist, and list the intervals on which the function is increasing, decreasing or constant.
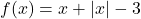
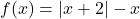
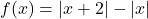
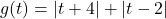
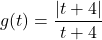
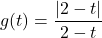
- With the help of your classmates, write an absolute value function whose graph is given below.
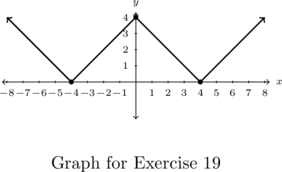
In Exercises 20 – 31, solve the equation.
Solve the equations in Exercises 32 – 37 using the property that if ![]() then
then ![]() .
.
In Exercises 38 – 53, solve the inequality. Write your answer using interval notation.
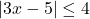
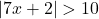
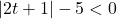
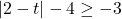
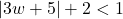
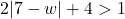

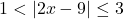
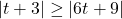
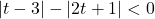
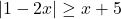
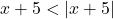
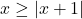
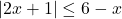
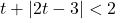
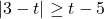
- Show that if
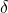 is a real number with
is a real number with 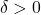 , the solution to
, the solution to 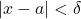 is the interval:
is the interval: 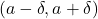 . That is, an interval centered at
. That is, an interval centered at  with `radius’
with `radius’ 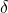 .
. - The Triangle Inequality for real numbers states that for all real numbers
 and
and  ,
, 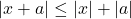 and, moreover,
and, moreover, 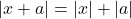 if and only if
if and only if  and
and  are both positive, both negative, or one or the other is
are both positive, both negative, or one or the other is 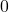 . Graph each pair of functions below on the same pair of axes and use the graphs to verify the triangle inequality in each instance.
. Graph each pair of functions below on the same pair of axes and use the graphs to verify the triangle inequality in each instance.
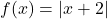 and
and 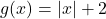 .
.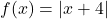 and
and 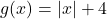 .
.
Section 1.4 Exercise Answers can be found in the Appendix … Coming soon
- More generally,
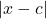 is the distance from
is the distance from  to
to  on the number line. ↵
on the number line. ↵ - We know it's complete because we did the Math - no trusting technology on this example! ↵
- See the Ways to Represent a Function box at the end of Section 1.2. Also, we use `
 ' as our dummy variable to avoid the confusion that would arise by over-using `
' as our dummy variable to avoid the confusion that would arise by over-using ` '. ↵
'. ↵ - That is, every real number
 can be written as
can be written as 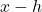 for some
for some  , and every real number
, and every real number  can be written as
can be written as 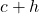 for some
for some  . ↵
. ↵ - See the discussion following Example 1.2.1 regarding the plot of Skippy's data. ↵
- See the Reflections box in Section 1.1. ↵
- Alternatively, setting
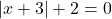 gives
gives 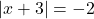 . Absolute values are never negative, thus we have no solution. ↵
. Absolute values are never negative, thus we have no solution. ↵ - We'll return to this momentarily. ↵
- Solving
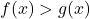 is equivalent to solving
is equivalent to solving 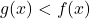 - that is, finding where the graph of
- that is, finding where the graph of  is below the graph of
is below the graph of  . ↵
. ↵ - See Theorem1.3. ↵
- Our picture shows only one of the solutions. We encourage you to take the time with a graphing utility to get the picture to show both points of intersection. ↵
- See Example 0.6.1 for examples of linear compound inequalities. ↵
- The underlying concept of Calculus can be phrased in terms of tolerances, so this is well worth your attention. ↵
- This means that for
 ,
, 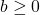 , if
, if 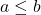 , then
, then 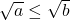 . ↵
. ↵
The distance between 0 and a number on the number line.

