2.2 Properties of Polynomial Functions and Their Graphs
2.2.1 Monomial Function
Definition 2.4
A monomial function is a function of the form
![]()
where ![]() and
and ![]() are real numbers,
are real numbers, ![]() and
and ![]() .
.
The domain of a monomial function is ![]() .
.
Monomial functions, by definition, contain the constant functions along with a two parameter family of functions, ![]() . We use
. We use ![]() as the default independent variable here with
as the default independent variable here with ![]() and
and ![]() as parameters. From Section 0.1.1, we recall that the set
as parameters. From Section 0.1.1, we recall that the set ![]() is the set of natural numbers, so examples of monomial functions include
is the set of natural numbers, so examples of monomial functions include ![]() ,
, ![]() , and
, and ![]() . Note that the function
. Note that the function ![]() is not a monomial function. Even though
is not a monomial function. Even though ![]() for all nonzero values of
for all nonzero values of ![]() ,
, ![]() is undefined,[1] and hence
is undefined,[1] and hence ![]() does not have a domain of
does not have a domain of ![]() .[2]
.[2]
We begin our study of the graphs of polynomial functions by studying graphs of monomial functions. Starting with ![]() where
where ![]() is even, we investigate the cases
is even, we investigate the cases ![]() ,
, ![]() and
and ![]() . Numerically, we see that if
. Numerically, we see that if ![]() ,
, ![]() becomes much smaller as
becomes much smaller as ![]() increases whereas if
increases whereas if ![]() or
or ![]() ,
, ![]() becomes much larger as
becomes much larger as ![]() increases. These trends manifest themselves geometrically as the graph `flattening’ for
increases. These trends manifest themselves geometrically as the graph `flattening’ for ![]() and `narrowing’ for
and `narrowing’ for ![]() as
as ![]() increases.[3]
increases.[3]
![Rendered by QuickLaTeX.com \[\begin{array}{|r||c|c|c|} \hline x & x^2 & x^4 & x^6 \\ \hline -2 & 4& 16& 64 \\ \hline -1 & 1 & 1& 1\\ \hline -0.5 & 0.25 & 0.0625& 0.015625 \\ \hline 0 & 0 & 0 & 0 \\ \hline 0.5 & 0.25 & 0.0625 & 0.015625 \\ \hline 1& 1 & 1& 1 \\ \hline 2 & 4 & 16 & 64 \\ \hline \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-cbafe3ca3efed1ddae328fdbce3e3322_l3.png)
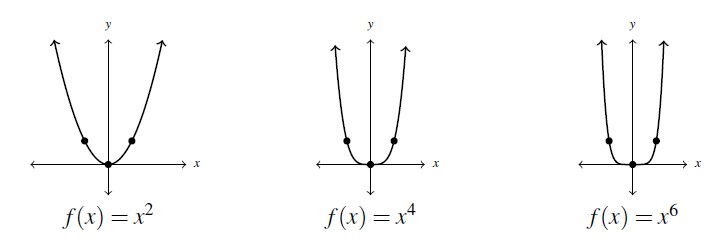
From the graphs, it appears as if the range of each of these functions is ![]() . When
. When ![]() is even,
is even, ![]() for all
for all ![]() so the range of
so the range of ![]() is contained in
is contained in ![]() . To show that the range of
. To show that the range of ![]() is all of
is all of ![]() , we note that the equation
, we note that the equation ![]() for
for ![]() has (at least) one solution for every even integer
has (at least) one solution for every even integer ![]() , namely
, namely ![]() . (See Section 0.2 for a review of this notation.) Hence,
. (See Section 0.2 for a review of this notation.) Hence, ![]() which shows that every non-negative real number is in the range of
which shows that every non-negative real number is in the range of ![]() .[4]
.[4]
Another item worthy of note is the symmetry about the line ![]() a.k.a the
a.k.a the ![]() -axis. (See Definition ?? for a review of this concept.) With
-axis. (See Definition ?? for a review of this concept.) With ![]() being even,
being even, ![]() . At the level of points, we have that for all
. At the level of points, we have that for all ![]() ,
, ![]() . Hence for every point
. Hence for every point ![]() on the graph of
on the graph of ![]() , the point symmetric about the
, the point symmetric about the ![]() -axis,
-axis, ![]() is on the graph, too. We give this sort of symmetry a name honoring its roots here with even-powered monomial functions:
is on the graph, too. We give this sort of symmetry a name honoring its roots here with even-powered monomial functions:
Definition 2.5
A function ![]() is said to be even if
is said to be even if ![]() for all
for all ![]() in the domain of
in the domain of ![]() .
.
NOTE: A function ![]() is even if and only if the graph of
is even if and only if the graph of ![]() is symmetric about the
is symmetric about the ![]() -axis.
-axis.
An investigation of the odd powered monomial functions (![]() ) yields similar results with the major difference being that when a negative number is raised to an odd natural number power the result is still negative. Numerically we see that for
) yields similar results with the major difference being that when a negative number is raised to an odd natural number power the result is still negative. Numerically we see that for ![]() the values of
the values of ![]() increase as
increase as ![]() increases and for
increases and for ![]() the values of
the values of ![]() get closer to
get closer to ![]() as
as ![]() increases. This translates graphically into a flattening behavior on the interval
increases. This translates graphically into a flattening behavior on the interval ![]() and a narrowing elsewhere. The graphs are shown below.
and a narrowing elsewhere. The graphs are shown below.
The range of these functions appear to be all real numbers, ![]() which is algebraically sound as the equation
which is algebraically sound as the equation ![]() has a solution for every real number,[5] namely
has a solution for every real number,[5] namely ![]() . Hence, for every real number
. Hence, for every real number ![]() , choose
, choose ![]() so that
so that ![]() . This shows that every real number is in the range of
. This shows that every real number is in the range of ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{array}{|r||c|c|c|} \hline x & x^3 & x^5 & x^7 \\ \hline -2 & -8& -32& -128 \\ \hline -1 & -1 & -1& -1\\ \hline -0.5 & 0.125 & -0.03125& -0.0078125 \\ \hline 0 & 0 & 0 & 0 \\ \hline 0.5 & 0.125 & 0.03125 & 0.0078125 \\ \hline 1& 1 & 1& 1 \\ \hline 2 & 8 & 32 & 128 \\ \hline \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e34021d8cb5e182443beef0513d58ba3_l3.png)
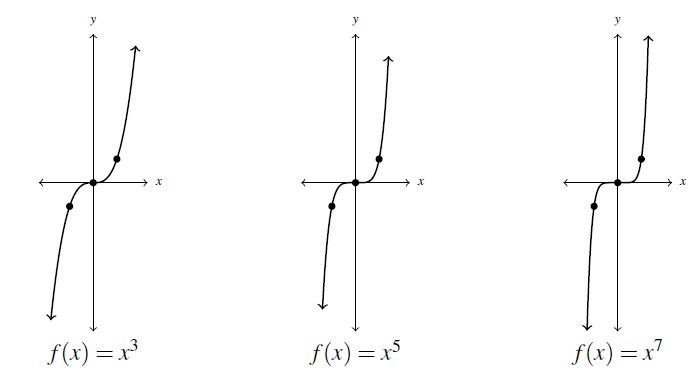
Here, as a result of ![]() being odd,
being odd, ![]() . This means that whenever
. This means that whenever ![]() is on the graph, so is the point symmetric about the origin,
is on the graph, so is the point symmetric about the origin, ![]() . (Again, see Definition 1.1.) We generalize this property below. Not surprisingly, we name it in honor of its odd powered heritage:
. (Again, see Definition 1.1.) We generalize this property below. Not surprisingly, we name it in honor of its odd powered heritage:
Definition 2.6
A function ![]() is said to be odd if
is said to be odd if ![]() for all
for all ![]() in the domain of
in the domain of ![]() .
.
NOTE: A function ![]() is odd if and only if the graph of
is odd if and only if the graph of ![]() is symmetric about the origin.
is symmetric about the origin.
The most important thing to take from the discussion above is the basic shape and common points on the graphs of ![]() for each of the families when
for each of the families when ![]() even and
even and ![]() is odd. While symmetry is nice and should be noted when present, even and odd symmetry are comparatively rare. The point of Definitions 2.5 and 2.6 is to give us the vocabulary to point out the symmetry when appropriate.
is odd. While symmetry is nice and should be noted when present, even and odd symmetry are comparatively rare. The point of Definitions 2.5 and 2.6 is to give us the vocabulary to point out the symmetry when appropriate.
Moving on, we take a cue from Theorem 1.4 and prove the following.
Theorem 2.2
For real numbers ![]() ,
, ![]() and
and ![]() with
with ![]() , the graph of
, the graph of ![]() can be obtained from the graph of
can be obtained from the graph of ![]() by performing the following operations, in sequence:
by performing the following operations, in sequence:
- add
 to the
to the  -coordinates of each of the points on the graph of
-coordinates of each of the points on the graph of  . This results in a horizontal shift to the right if
. This results in a horizontal shift to the right if 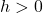 or left if
or left if 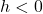 .
.
NOTE: This transforms the graph of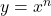 to
to 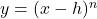 .
. - multiply the
 -coordinates of each of the points on the graph obtained in Step 1 by
-coordinates of each of the points on the graph obtained in Step 1 by  . This results in a vertical scaling, but may also include a reflection about the
. This results in a vertical scaling, but may also include a reflection about the  -axis if
-axis if 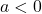 .
.
NOTE: This transforms the graph of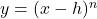 to
to 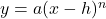 .
. - add
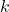 to the
to the  -coordinates of each of the points on the graph obtained in Step 2. This results in a vertical shift up if
-coordinates of each of the points on the graph obtained in Step 2. This results in a vertical shift up if 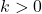 or down if
or down if 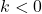 .
.
NOTE: This transforms the graph of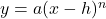 to
to 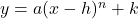
Proof. Our goal is to start with the graph of ![]() and build it up to the graph of
and build it up to the graph of ![]() . We begin by examining
. We begin by examining ![]() . The graph of
. The graph of ![]() can be described as the set of points
can be described as the set of points ![]() .[6] Likewise, the graph of
.[6] Likewise, the graph of ![]() can be described as the set of points
can be described as the set of points ![]() . If we re-label
. If we re-label ![]() so that
so that ![]() , then as
, then as ![]() varies through all real numbers so does
varies through all real numbers so does ![]() .[7] Hence, we can describe the graph of
.[7] Hence, we can describe the graph of ![]() as
as ![]() . This means that we can obtain the graph of
. This means that we can obtain the graph of ![]() from the graph of
from the graph of ![]() by adding
by adding ![]() to each of the
to each of the ![]() -coordinates of the points on the graph of
-coordinates of the points on the graph of ![]() and that establishes the first step of the theorem.
and that establishes the first step of the theorem.
Next, we consider the graph of ![]() as compared to the graph of
as compared to the graph of ![]() . The graph of
. The graph of ![]() is the set of points
is the set of points ![]() while the graph of
while the graph of ![]() is the set of points
is the set of points ![]() . The only difference between the points
. The only difference between the points ![]() and
and ![]() is that the
is that the ![]() -coordinate in the latter is
-coordinate in the latter is ![]() times the
times the ![]() -coordinate of the former.
-coordinate of the former.
In other words, to produce the graph of ![]() from the graph of
from the graph of ![]() , we take the
, we take the ![]() -coordinate of each point on the graph of
-coordinate of each point on the graph of ![]() and multiply it by
and multiply it by ![]() to get the corresponding point on the graph of
to get the corresponding point on the graph of ![]() . If
. If ![]() , all we are doing is scaling the
, all we are doing is scaling the ![]() -axis by
-axis by ![]() . If
. If ![]() , then, in addition to scaling the
, then, in addition to scaling the ![]() -axis, we are also reflecting each point across the
-axis, we are also reflecting each point across the ![]() -axis. In either case, we have established the second step of the theorem.
-axis. In either case, we have established the second step of the theorem.
Last, we compare the graph of ![]() to that of
to that of ![]() . Once again, we view the graphs as sets of points in the plane. The graph of
. Once again, we view the graphs as sets of points in the plane. The graph of ![]() is
is ![]() and the graph of
and the graph of ![]() is
is![]() . Looking at the corresponding points,
. Looking at the corresponding points, ![]() and
and ![]() , we see that we can obtain all of the points on the graph of
, we see that we can obtain all of the points on the graph of ![]() by adding
by adding ![]() to each of the
to each of the ![]() -coordinates to points on the graph of
-coordinates to points on the graph of ![]() . This is equivalent to shifting every point vertically by
. This is equivalent to shifting every point vertically by ![]() units which establishes the third and final step in the theorem.
units which establishes the third and final step in the theorem. ![]()
This argument should sound familiar. The proof we presented above is more-or-less the same argument we presented after the proof of Theorem 1.4 in Section 1.4 but with `![]() ‘ replaced by `
‘ replaced by `![]() .’ Also note that using
.’ Also note that using ![]() in Theorem 2.2 establishes Theorem 2.1 in Section 2.1.
in Theorem 2.2 establishes Theorem 2.1 in Section 2.1.
We now use Theorem 2.2 to graph two different “transformed” monomial functions. To provide the reader an opportunity to compare and contrast the graphical behaviors exhibited in the case when ![]() is even versus when
is even versus when ![]() is odd, we graph one of each case.
is odd, we graph one of each case.
Example 2.2.1
Example 2.2.1.1
Use Theorem 2.2 to graph the following functions. Label at least three points on each graph. State the domain and range using interval notation.
![]()
Solution:
Graph ![]() .
.
For ![]() , we identify
, we identify ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Thus to graph
. Thus to graph ![]() , we start with
, we start with ![]() and perform the following steps, in sequence, tracking the points
and perform the following steps, in sequence, tracking the points ![]() ,
, ![]() and
and ![]() through each step:
through each step:
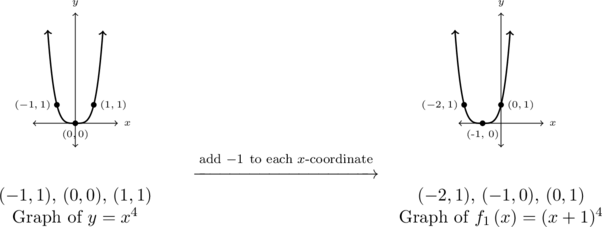
Step 1: add ![]() to the
to the ![]() -coordinates of each of the points on the graph of
-coordinates of each of the points on the graph of ![]() :
:
Step 2: multiply the ![]() -coordinates of each of the points on the graph of
-coordinates of each of the points on the graph of ![]() by
by ![]() :
:
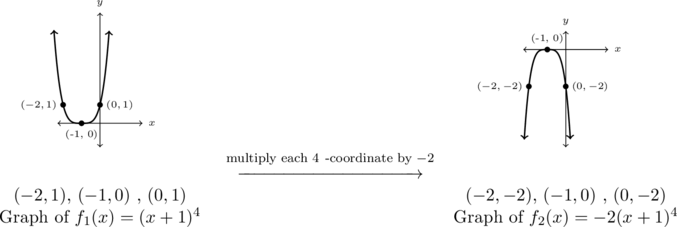
Step 3: add ![]() to the
to the ![]() -coordinates of each of the points on the graph of
-coordinates of each of the points on the graph of ![]() :
:

The domain here is ![]() , while the range is
, while the range is ![]() .
.
Example 2.2.1.2
Use Theorem 2.2 to graph the following functions. Label at least three points on each graph. State the domain and range using interval notation.
![]()
Solution:
Graph ![]() .
.
To use Theorem 2.2 to graph ![]() , we must first rewrite the expression for
, we must first rewrite the expression for ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(t) &=& \dfrac{(2t-1)^3}{5} \\[8pt] &=& \frac{1}{5} \left( 2 \left(t - \frac{1}{2} \right) \right)^3 \\[8pt] &=& \frac{1}{5} (2)^3 \left( t - \frac{1}{2} \right)^3 \\[8pt] &=& \frac{8}{5} \left( t - \frac{1}{2} \right)^3 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-820bfc326ca416aa3c4b040413db3948_l3.png)
We identify ![]() ,
, ![]() and
and ![]() . Hence, we start with the graph of
. Hence, we start with the graph of ![]() and perform the following steps, in sequence, tracking the points
and perform the following steps, in sequence, tracking the points ![]() ,
, ![]() and
and ![]() through each step:
through each step:
Step 1: add ![]() to each of the
to each of the ![]() -coordinates of each of the points on the graph of
-coordinates of each of the points on the graph of ![]() :
:
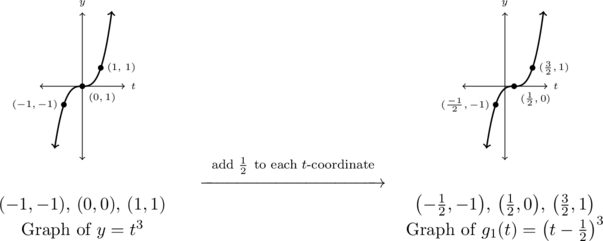
Step 2: multiply each of the ![]() -coordinates of the graph of
-coordinates of the graph of ![]() by
by ![]() .
.
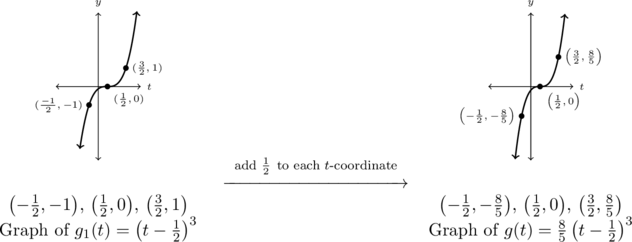
Both the domain and range of ![]() is
is ![]() .
.
Example 2.2.1 demonstrates two big ideas in mathematics: first, resolving a complex problem into smaller, simpler steps, and, second, the value of changing form.
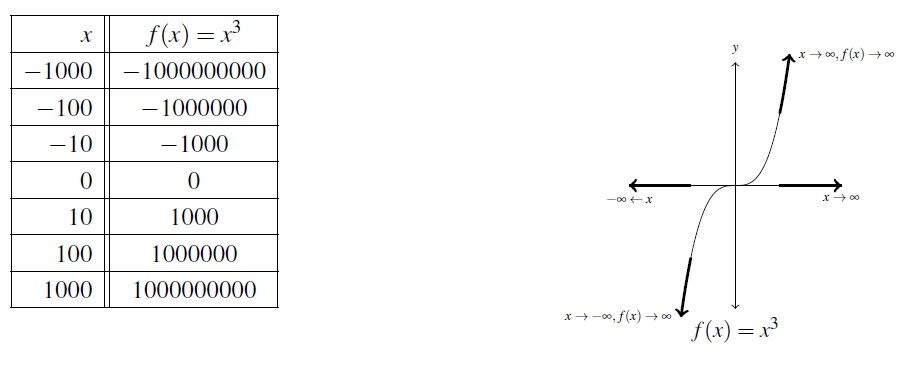
Next we wish to focus on the so-called end behavior presented in each case.[8] The end behavior of a function is a way to describe what is happening to the outputs from a function as the inputs approach the `ends’ of the domain. Due to the fact that the domain of monomial functions is ![]() , we are looking to see what these functions do as their inputs `approach’
, we are looking to see what these functions do as their inputs `approach’ ![]() . The best we can do is sample inputs and outputs and infer general behavior from these observations.\footnote{and let Calculus students prove our claims.} The good news is we’ve wrestled with this concept before. Indeed, every time we add `arrows’ to the graph of a function, we’ve indicated its end behavior. Let’s revisit the graph of
. The best we can do is sample inputs and outputs and infer general behavior from these observations.\footnote{and let Calculus students prove our claims.} The good news is we’ve wrestled with this concept before. Indeed, every time we add `arrows’ to the graph of a function, we’ve indicated its end behavior. Let’s revisit the graph of ![]() using the table below.
using the table below.

As ![]() takes on smaller and smaller values,[9], we see
takes on smaller and smaller values,[9], we see ![]() takes on larger and larger positive values. The smaller
takes on larger and larger positive values. The smaller ![]() we use, the larger the
we use, the larger the ![]() becomes, seemingly without bound.[10] We codify this behavior by writing as
becomes, seemingly without bound.[10] We codify this behavior by writing as ![]() ,
, ![]() . Graphically, the farther to the left we travel on the
. Graphically, the farther to the left we travel on the ![]() -axis, the farther up the
-axis, the farther up the ![]() -axis the function values travel. This is why we use an `arrow’ on the graph in Quadrant II heading upwards to the left. Similarly, we write as
-axis the function values travel. This is why we use an `arrow’ on the graph in Quadrant II heading upwards to the left. Similarly, we write as ![]() ,
, ![]() because as the
because as the ![]() values increase, so do the
values increase, so do the ![]() values – seemingly without bound. Graphically we indicate this by an arrow on the graph in Quadrant I heading upwards to the right. This behavior holds for all functions
values – seemingly without bound. Graphically we indicate this by an arrow on the graph in Quadrant I heading upwards to the right. This behavior holds for all functions ![]() where
where ![]() is even.
is even.
Repeating this investigation for ![]() , we find as
, we find as ![]() ,
, ![]() becomes unbounded in the negative direction, so we write
becomes unbounded in the negative direction, so we write ![]() . As
. As ![]() ,
, ![]() becomes unbounded in the positive direction, so we write
becomes unbounded in the positive direction, so we write ![]() . This trend holds for all functions
. This trend holds for all functions ![]() where
where ![]() is odd.
is odd.
Theorem 2.3 summarizes the end behavior of monomial functions. The results are a consequence of Theorem 2.2 in that the end behavior of a function of the form ![]() only differs from that of
only differs from that of ![]() if there is a reflection, that is, if
if there is a reflection, that is, if ![]() .
.
Theorem 2.3 End Behavior of Monomial Functions
Suppose ![]() where
where ![]() is a real number and
is a real number and ![]() .
.
- If
 is even:
is even:
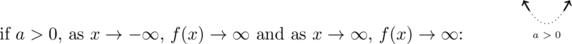
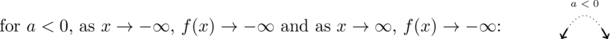
- If
 is odd:
is odd:
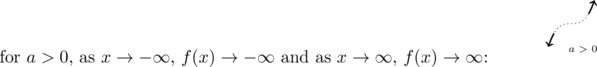
2.2.2 Polynomial Functions
We are now in the position to discuss polynomial functions. Simply stated, polynomial functions are sums of monomial functions. The challenge becomes how to describe one of these beasts in general. Up until now, we have used distinct letters to indicate different parameters in our definitions of function families. In other words, we define constant functions as ![]() , linear functions as
, linear functions as ![]() , and quadratic functions as
, and quadratic functions as ![]() . We even hinted at a function of the form
. We even hinted at a function of the form ![]() . What happens if we wanted to describe a generic polynomial that required, say, 117 different parameters? Our work around is to use subscripted parameters,
. What happens if we wanted to describe a generic polynomial that required, say, 117 different parameters? Our work around is to use subscripted parameters, ![]() , that denote the coefficient of
, that denote the coefficient of ![]() . For example, instead of writing a quadratic as
. For example, instead of writing a quadratic as ![]() , we describe it as
, we describe it as ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() are real numbers and
are real numbers and ![]() . As an added example, consider
. As an added example, consider ![]() . We can re-write the formula for
. We can re-write the formula for ![]() as
as ![]() and identify
and identify ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() . This is the notation we use in the following definition.
. This is the notation we use in the following definition.
Definition 2.7
A polynomial function is a function of the form
![]()
where ![]() ,
, ![]() ,
, ![]() ,
, ![]() are real numbers and
are real numbers and ![]()
The domain of a polynomial function is ![]()
As usual, ![]() is used in Definition 2.7 as the independent variable with the
is used in Definition 2.7 as the independent variable with the ![]() each being a parameter. Even though we specify
each being a parameter. Even though we specify ![]() so
so ![]() , the value of the
, the value of the ![]() are unrestricted. Hence, any constant function
are unrestricted. Hence, any constant function ![]() can be written as
can be written as ![]() , and so they are polynomials. Polynomials have an associated vocabulary, and hence, so do polynomial functions.
, and so they are polynomials. Polynomials have an associated vocabulary, and hence, so do polynomial functions.
Definition 2.8
- Given
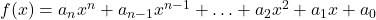 with
with 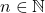 and
and 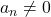 , we say
, we say
- The natural number
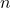 is called the degree of the polynomial
is called the degree of the polynomial  .
. - The term
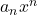 is called the leading term of the polynomial
is called the leading term of the polynomial  .
. - The real number
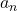 is called the leading coefficient of the polynomial
is called the leading coefficient of the polynomial  .
. - The real number
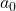 is called the constant term of the polynomial
is called the constant term of the polynomial  .
.
- The natural number
- If
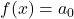 , and
, and 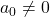 , we say
, we say  has degree
has degree 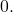
- If
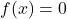 , we say
, we say  has no degree.[11]
has no degree.[11]
Again, constant functions are split off in their own separate case Definition 2.8 because of the ambiguity of ![]() . (See the remarks following Definition 2.4.) A consequence of Definition 2.8 is that we can now think of nonzero constant functions as `zeroth’ degree polynomial functions, linear functions as `first’ degree polynomial functions, and quadratic functions as `second’ degree polynomial functions.
. (See the remarks following Definition 2.4.) A consequence of Definition 2.8 is that we can now think of nonzero constant functions as `zeroth’ degree polynomial functions, linear functions as `first’ degree polynomial functions, and quadratic functions as `second’ degree polynomial functions.
Example 2.2.2
Example 2.2.2.1
Determine the degree, leading term, leading coefficient and constant term of the following polynomial functions.
![]()
Solution:
Determine the degree, leading term, leading coefficient and constant term of ![]() .
.
There are no surprises with ![]() . It is written in the form of Definition 2.8, and we see that
. It is written in the form of Definition 2.8, and we see that
the degree is ![]() ,
,
the leading term is ![]() ,
,
the leading coefficient is ![]() , and
, and
the constant term is ![]() .
.
Example 2.2.2.2
Determine the degree, leading term, leading coefficient and constant term of the following polynomial functions.
![]()
Solution:
Determine the degree, leading term, leading coefficient and constant term of ![]() .
.
Two changes here: first, the independent variable is ![]() , not
, not ![]() . Second, the form given in Definition 2.8 specifies the function be written in descending order of the powers of
. Second, the form given in Definition 2.8 specifies the function be written in descending order of the powers of ![]() , or in this case,
, or in this case, ![]() . To that end, we re-write
. To that end, we re-write ![]() and see that
and see that
the degree of ![]() is
is ![]() ,
,
the leading term is ![]() ,
,
the leading coefficient is ![]() , and
, and
the constant term is ![]() .
.
Example 2.2.2.3
Determine the degree, leading term, leading coefficient and constant term of the following polynomial functions.
![]()
Solution:
Determine the degree, leading term, leading coefficient and constant term of ![]()
We need to rewrite the formula for ![]() so that it resembles the form given in Definition 2.8:
so that it resembles the form given in Definition 2.8:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} H(w) &=& \frac{4-w}{5} \\ &=& \frac{4}{5} - \frac{w}{5} \\ &=& -\frac{1}{5} w + \frac{4}{5} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e8f42fe0bf23e16fbbd2114a809a8b5c_l3.png)
We see
the degree of ![]() is
is ![]() ,
,
the leading term is ![]() ,
,
the leading coefficient is ![]() , and
, and
the constant term is ![]()
Example 2.2.2.4
Determine the degree, leading term, leading coefficient and constant term of the following polynomial functions.
![]()
Solution:
Determine the degree, leading term, leading coefficient and constant term of ![]()
It may seem that we have some work ahead of us to get ![]() in the form of Definition 2.8. However, it is possible to glean the information requested about
in the form of Definition 2.8. However, it is possible to glean the information requested about ![]() without multiplying out the entire expression
without multiplying out the entire expression ![]() The leading term of
The leading term of ![]() will be the term which has the highest power of
will be the term which has the highest power of ![]() . The way to get this term is to multiply the terms with the highest power of
. The way to get this term is to multiply the terms with the highest power of ![]() from each factor together – in other words, the leading term of
from each factor together – in other words, the leading term of ![]() is the product of the leading terms of the factors of
is the product of the leading terms of the factors of ![]() Hence, the leading term of
Hence, the leading term of ![]() is
is ![]()
This means that the degree of ![]() is
is ![]() and the leading coefficient is
and the leading coefficient is ![]()
As for the constant term, we can perform a similar operation. The constant term of ![]() is obtained by multiplying the constant terms from each of the factor:
is obtained by multiplying the constant terms from each of the factor: ![]()
We now turn our attention to graphs of polynomial functions. As polynomial functions are sums of monomial functions, it stands to reason that some of the properties of those graphs carry over to more general polynomials. We first discuss end behavior. Consider ![]() . Below are two graphs of
. Below are two graphs of ![]() (solid line) along with the graphs of its leading term,
(solid line) along with the graphs of its leading term, ![]() (dashed line.) On the left is a view `near’ the origin, while on the right is a `zoomed out’ view. Near the origin, the graphs have little in common, but as we look farther out, it becomes that the functions begin to look quite similar.
(dashed line.) On the left is a view `near’ the origin, while on the right is a `zoomed out’ view. Near the origin, the graphs have little in common, but as we look farther out, it becomes that the functions begin to look quite similar.
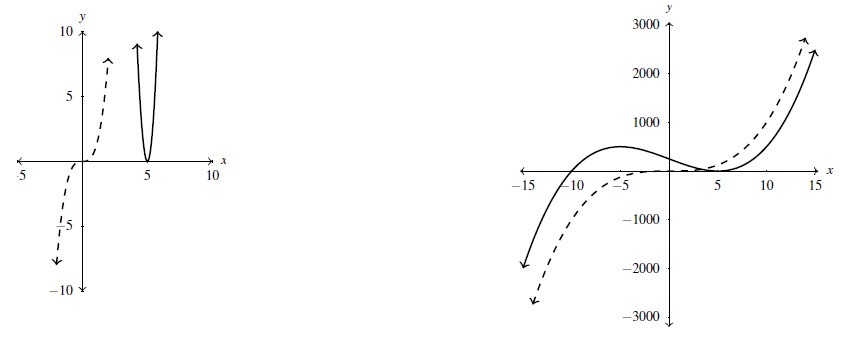
This observation is borne out numerically as well. Based on the table below, as ![]() , it certainly appears as if
, it certainly appears as if ![]() . One way to think about what is happening numerically is that the leading term
. One way to think about what is happening numerically is that the leading term ![]() dominates the lower order terms
dominates the lower order terms ![]() and
and ![]() as
as ![]() . In other words,
. In other words, ![]() grows so much faster than
grows so much faster than ![]() and
and ![]() that these `lower order terms’ don’t contribute anything of significance to the
that these `lower order terms’ don’t contribute anything of significance to the ![]() so
so ![]() . Another way to see this is to rewrite
. Another way to see this is to rewrite ![]() as[12]
as[12]
![Rendered by QuickLaTeX.com \[\begin{array}{rcl} f(x) &=& x^3 - 75x + 250 \\[10pt] &=& x^3 \left(1 - \frac{75}{x^2} + \frac{250}{x^3} \right) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-98c7a7ee3395b0f60a1ee397ed611f3d_l3.png)
As ![]() , both
, both ![]() and
and ![]() have constant numerators but denominators that are becoming unbounded. As such, both
have constant numerators but denominators that are becoming unbounded. As such, both ![]() and
and ![]() . Therefore, as
. Therefore, as ![]() ,
,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f(x) &=& x^3 - 75x+250 \\[10pt] &=& x^3 \left(1 - \frac{75}{x^2} + \frac{250}{x^3} \right) \\[10pt] &\approx& x^3 (1 + 0 + 0) = x^3 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-fc7789d8c04bfa1136bec04ab16d93c9_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{array}{|r||c|c|c|c|c|c|} \hline x & f(x) = x^3 -75x+250 & x^3 & -75 x & 250 & \frac{75}{x^2} & \frac{250}{x^3} \\ \hline -1000 & \approx -1 \times 10^9 & -1 \times 10^9 &75000 & 250 & 7.5 \times 10^{-5} & -2.5 \times 10^{-7} \\ \hline -100 & \approx -9.9 \times 10^5 & -1 \times 10^6 & 7500 & 250 & 0.0075 & -2.5 \times 10^{-4} \\ \hline -10 & 0 & -1000 & 750 & 250 & 0.75 & -0.25\\ \hline 10 & 500 & 1000 & -750 & 250 & 0.75 & 0.25 \\ \hline 100 &\approx 9.9 \times 10^5 & 1 \times 10^6 & -7500 & 250 & 0.0075 & 2.5 \times 10^{-4} \\ \hline 1000 & \approx 1 \times 10^9 & 1 \times 10^9 & -75000 & 250 & 7.5 \times 10^{-5} & 2.5 \times 10^{-7} \\ \hline \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-57ef81ae0859550bdbf7b19a450975d9_l3.png)
Next, consider ![]() . Following the logic of the above example, we would expect the end behavior of
. Following the logic of the above example, we would expect the end behavior of ![]() to mimic that of
to mimic that of ![]() . When we graph
. When we graph ![]() (solid line) on the same set of axes as
(solid line) on the same set of axes as ![]() (dashed line), a view near the origin seems to suggest the exact opposite. However, zooming out reveals that the two graphs do share the same end behavior.[13]
(dashed line), a view near the origin seems to suggest the exact opposite. However, zooming out reveals that the two graphs do share the same end behavior.[13]
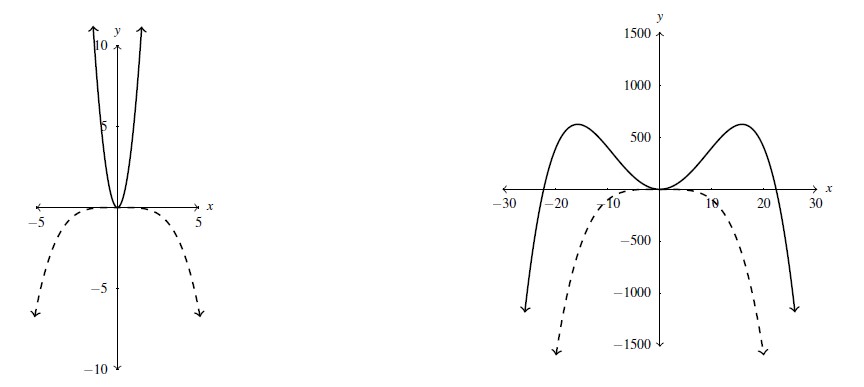
Algebraically, for ![]() , even with the small coefficient of
, even with the small coefficient of ![]() ,
, ![]() dominates the
dominates the ![]() term so
term so ![]() . More precisely,
. More precisely,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(x) &=& -0.01x^4+5x^2 \\[10pt] &=& x^4 \left(-0.01 + \frac{5}{x^2} \right)\\[10pt] &\approx& x^4(-0.01 + 0) \\[10pt] &=& -0.01x^4 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-cc8f12716d5ae8d6f27fa29edf1297f1_l3.png)
The results of these last two examples are generalized below in Theorem 2.4.
Theorem 2.4 End Behavior for Polynomial Functions
The end behavior of polynomial function ![]() with
with ![]() matches the end behavior of
matches the end behavior of ![]() .
.
That is, the end behavior of a polynomial function is determined by its leading term.
We argue Theorem 2.4 using an argument similar to ones used above. As ![]() ,
,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f(x) &=& x^{n} \left( a_{n} +\dfrac{a_{n-1}}{x}+ \ldots + \dfrac{a_{2}}{x^{n-2}} + \dfrac{a_{1}}{x^{n-1}}+\dfrac{a_{0}}{x^{n}}\right) \\[10pt] &\approx& x^n( a_{n} + 0 +\ldots 0) \\[8pt] &=& a_{n} x^n \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d2ecbc249ab2f7588b3dba7181531197_l3.png)
If this argument looks a little fuzzy, it should. In Calculus, we have the tools necessary to more explicitly state what we mean by ![]() . For now, we’ll rely on number sense and algebraic intuition.[14]
. For now, we’ll rely on number sense and algebraic intuition.[14]
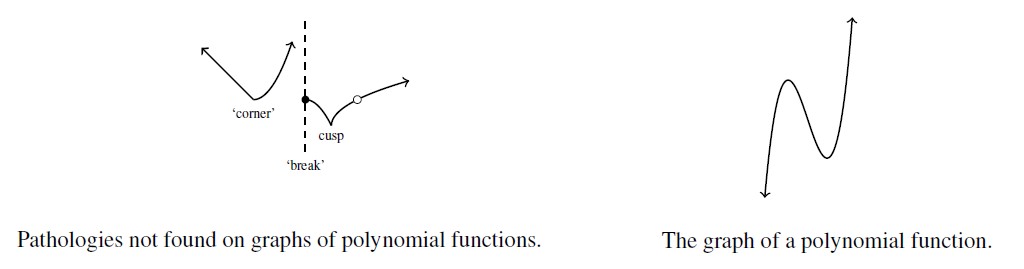
Now that we know how to determine the end behavior of polynomial functions, it’s time to investigate what happens `in between’ the ends. First and foremost, polynomial functions are continuous. Recall from Section 2.1 that, informally, graphs of continuous functions have no `breaks’ or `holes’ in them.[15] Monomial functions are continuous (as far as we can tell) and polynomials are sums of monomial functions, so we conclude that polynomial functions are continuous as well. Moreover, the graphs of monomial functions, hence polynomial functions, are smooth. Once again, `smoothness’ is a concept defined precisely in Calculus, but for us, functions have no `corners’ or `sharp turns’. Below we find the graph of a function which is neither smooth nor continuous, and to its right we have a graph of a polynomial, for comparison. The function whose graph appears on the left fails to be continuous where it has a `break’ or `hole’ in the graph; everywhere else, the function is continuous. The function is continuous at the `corner’ and the `cusp’, but we consider these `sharp turns’, so these are places where the function fails to be smooth. Apart from these four places, the function is smooth and continuous. Polynomial functions are smooth and continuous everywhere, as exhibited in the graph on the right. The notion of smoothness is what tells us graphically that, for example, ![]() , whose graph is the characteristic `
, whose graph is the characteristic `![]() ‘ shape, cannot be a polynomial function, even though it is a piecewise-defined function comprised of polynomial functions. Knowing polynomial functions are continuous and smooth gives us an idea of how to `connect the dots’ when sketching the graph from points that we’re able to find analytically such as intercepts.
‘ shape, cannot be a polynomial function, even though it is a piecewise-defined function comprised of polynomial functions. Knowing polynomial functions are continuous and smooth gives us an idea of how to `connect the dots’ when sketching the graph from points that we’re able to find analytically such as intercepts.
Speaking of intercepts, we next focus our attention on the behavior of the graphs of polynomial functions near their zeros. Recall a zero ![]() of a function
of a function ![]() is a solution to
is a solution to ![]() . Geometrically, the zeros of a function are the
. Geometrically, the zeros of a function are the ![]() -coordinates of the
-coordinates of the ![]() -intercepts of the graph of
-intercepts of the graph of ![]() .
.
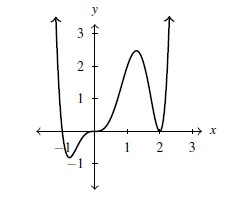
Consider the polynomial function ![]() .
.
To find the zeros of ![]() , we set
, we set ![]() . The expression
. The expression ![]() is already factored, so we set each factor equal to zero.[16]
is already factored, so we set each factor equal to zero.[16]
Solving ![]() gives
gives ![]() ,
, ![]() gives
gives ![]() , and
, and ![]() gives
gives ![]() . Hence, our zeros are
. Hence, our zeros are ![]() ,
, ![]() , and
, and ![]() .
.
Below, we graph ![]() and observe the
and observe the ![]() -intercepts
-intercepts ![]() ,
, ![]() and
and ![]() . We first note that the graph crosses through the
. We first note that the graph crosses through the ![]() -axis at
-axis at ![]() and
and ![]() , but the graph touches and rebounds at
, but the graph touches and rebounds at ![]() . Moreover, at
. Moreover, at ![]() , the graph crosses through the axis is a fairly `linear’ fashion whereas there is a substantial amount of `flattening’ going on near
, the graph crosses through the axis is a fairly `linear’ fashion whereas there is a substantial amount of `flattening’ going on near ![]() . Our aim is to explain these observations and generalize them.
. Our aim is to explain these observations and generalize them.
First, let’s look at what’s happening with the formula ![]() when
when ![]() . We know the
. We know the ![]() -intercept at
-intercept at ![]() is due to the presence of the
is due to the presence of the ![]() factor in the expression for
factor in the expression for ![]() . So, in this sense, the factor
. So, in this sense, the factor ![]() is determining a major piece of the behavior of the graph near
is determining a major piece of the behavior of the graph near ![]() . For that reason, we focus instead on the other two factors to see what contribution they make. We find when
. For that reason, we focus instead on the other two factors to see what contribution they make. We find when ![]() ,
, ![]() and
and ![]() .
.
Hence,
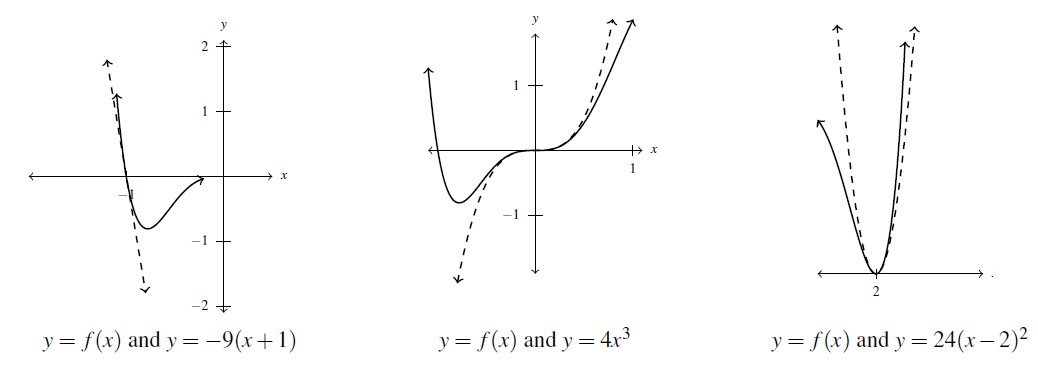
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f(x) &=& x^3 (x-2)^2 (x+1) \\ &\approx& (-1)^3 (-1-2)^2 (x+1)\\ &=& -9(x+1) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-1dd39717c944ee730f5eaa3ae6fc07c0_l3.png)
Below on the left is a graph of ![]() (the solid line) and the graph of
(the solid line) and the graph of ![]() (the dashed line.) Sure enough, these graphs approximate one another near
(the dashed line.) Sure enough, these graphs approximate one another near ![]() .
.
Likewise, let’s look near ![]() . The
. The ![]() -intercept
-intercept ![]() is a result of the
is a result of the ![]() factor. For
factor. For ![]() ,
, ![]() and
and ![]() , so
, so
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f(x) &=& x^3 (x-2)^2 (x+1)\\ &\approx& x^3 (-2)^2(1) \\ &=& 4x^3 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5aeb6351488f1f6204cf12bab72142c8_l3.png)
Below in the center picture, we have the graph of ![]() (again, the solid line) and
(again, the solid line) and ![]() (the dashed line) near
(the dashed line) near ![]() . Once again, the graphs verify our analysis.
. Once again, the graphs verify our analysis.
Last, but not least, we analyze ![]() near
near ![]() . Here, the intercept
. Here, the intercept ![]() is due to the
is due to the ![]() factor, so we look at the
factor, so we look at the ![]() and
and ![]() factors. If
factors. If ![]() ,
, ![]() and
and ![]() . Hence,
. Hence,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f(x) &=& x^3 (x-2)^2 (x+1) \\ &\approx& (2)^3 (x-2)^2 (2+1) \\ &=& 24(x-2)^2 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-86efa81cabf50265c2bf52d118db9d4f_l3.png)
Sure enough, as evidenced below on the right, the graphs of ![]() and
and ![]() .
.
We generalize our observations in Theorem 2.5 below. Like many things we’ve seen in this text, a more precise statement and proof can be found in a course on Calculus.
Theorem 2.5
Suppose ![]() is a polynomial function and
is a polynomial function and ![]() where
where ![]() and
and ![]() . Then the the graph of
. Then the the graph of ![]() near
near ![]() resembles that of
resembles that of ![]() .
.
Let’s see how Theorem 2.5 applies to our findings regarding ![]()
For ![]() ,
, ![]() . We rewrite
. We rewrite ![]() and identify
and identify ![]() and
and ![]() . We find
. We find ![]() so Theorem 2.5 says that near
so Theorem 2.5 says that near ![]() , the graph of
, the graph of ![]() resembles
resembles ![]() .
.
For ![]() ,
, ![]() and we can rewrite
and we can rewrite ![]() We identify
We identify ![]() and
and ![]() . In this case
. In this case ![]() , so Theorem 2.5 guarantees the graph of
, so Theorem 2.5 guarantees the graph of ![]() near
near ![]() resembles
resembles ![]()
Lastly, for ![]() , we see
, we see ![]() and we identify
and we identify ![]() and
and ![]() . We find
. We find ![]() , so Theorem 2.5 guarantees the graph of
, so Theorem 2.5 guarantees the graph of ![]() resembles
resembles ![]() near
near ![]() .
.
As we already mentioned, the formal statement and proof of Theorem 2.5 require Calculus. For now, we can understand the theorem as follows. If we factor a polynomial function as ![]() where
where ![]() , then
, then ![]() is a zero of
is a zero of ![]() , because
, because ![]() . The stipulation that
. The stipulation that ![]() means that we have essentially factored the expression
means that we have essentially factored the expression ![]() . Thinking back to Theorem 2.2, the graph
. Thinking back to Theorem 2.2, the graph ![]() has an
has an ![]() -intercept at
-intercept at ![]() , a basic overall shape determined by the exponent
, a basic overall shape determined by the exponent ![]() , and end behavior determined by the sign of
, and end behavior determined by the sign of ![]() . The fact that if
. The fact that if ![]() is a zero then we are guaranteed we can factor
is a zero then we are guaranteed we can factor ![]() were
were ![]() and, moreover, such a factorization is unique (so that there’s only one value of
and, moreover, such a factorization is unique (so that there’s only one value of ![]() possible for each zero) is a consequence of two theorems, Theorem 2.8 and The Factor Theorem, Theorem 2.10 which we’ll review in the next section. For now, we assume such a factorization is unique in order to define the following.
possible for each zero) is a consequence of two theorems, Theorem 2.8 and The Factor Theorem, Theorem 2.10 which we’ll review in the next section. For now, we assume such a factorization is unique in order to define the following.
Definition 2.9
Suppose ![]() is a polynomial function and
is a polynomial function and ![]() . If
. If ![]() where
where ![]() , we say
, we say ![]() is a zero of multiplicity
is a zero of multiplicity ![]() .
.
So, for ![]() ,
, ![]() is a zero of multiplicity
is a zero of multiplicity ![]() ,
, ![]() is a zero of multiplicity
is a zero of multiplicity ![]() , and
, and ![]() is a zero of multiplicity
is a zero of multiplicity ![]() . Theorems 2.4 and 2.5 give us the following:
. Theorems 2.4 and 2.5 give us the following:
Theorem 2.6 The Role of Multiplicity
Suppose ![]() is a polynomial function and
is a polynomial function and ![]() is a zero of multiplicity
is a zero of multiplicity ![]() .
.
- If
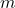 is even, the graph of
is even, the graph of 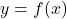 touches and rebounds from the
touches and rebounds from the  -axis at
-axis at  .
. - If
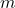 is odd, the graph of
is odd, the graph of 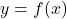 crosses through the
crosses through the  -axis at
-axis at 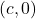 .
.
Steps for Constructing a Sign Diagram for a Polynomial Function
Suppose ![]() is a polynomial function.
is a polynomial function.
- Compute the zeros of
 and place them on the number line with the number
and place them on the number line with the number  above them.
above them. - Choose a real number, called a test value, in each of the intervals determined in step 1.
- Determine and record the sign of
 for each test value in step 2.
for each test value in step 2.
Theorem 2.7
Suppose ![]() is a polynomial of degree
is a polynomial of degree ![]() . Then
. Then ![]() has at most
has at most ![]() real zeros, counting multiplicities.
real zeros, counting multiplicities.
Connections Between Zeros, Factors and Graphs of Polynomial Functions
Suppose ![]() is a polynomial function of degree
is a polynomial function of degree ![]() . The following statements are equivalent:
. The following statements are equivalent:
- The real number
 is a zero of
is a zero of 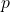
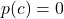
 is a solution to the polynomial equation
is a solution to the polynomial equation 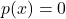
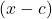 is a factor of
is a factor of 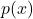
- The point
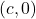 is an
is an  -intercept of the graph of
-intercept of the graph of 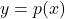
Our next example showcases how all of the above theories can assist in sketching relatively good graphs of polynomial functions without the assistance of technology.
Example 2.2.3
Example 2.2.3.1
Let ![]() . Compute all real zeros of
. Compute all real zeros of ![]() and state their multiplicities.
and state their multiplicities.
Solution:
Compute all real zeros of ![]() and state their multiplicities.
and state their multiplicities.
To find the zeros of ![]() , we set
, we set ![]() . The expression
. The expression ![]() is already (partially) factored, so we set each factor equal to
is already (partially) factored, so we set each factor equal to ![]() and solve.
and solve.
From ![]() , we get
, we get ![]() ;
;
from ![]() we get
we get ![]() ; and
; and
from solving ![]() we get
we get ![]() .
.
Hence, the zeros are ![]() ,
, ![]() , and
, and ![]() .
.
In order to determine the multiplicities, we need to factor ![]() as so we can identify the
as so we can identify the ![]() and
and ![]() as described in Definition 2.9.
as described in Definition 2.9.
The zero ![]() corresponds to the factor
corresponds to the factor ![]() . Notice, however, that writing
. Notice, however, that writing ![]() with
with ![]() and
and ![]() does not satisfy Definition 2.9 because,
does not satisfy Definition 2.9 because, ![]() . Indeed, we can factor
. Indeed, we can factor ![]() so that
so that
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} p(x) &=& (2x-1)(x+1)(1-x^4)\\ &=& (2x-1)(x+1)(1-x)(1+x)(x^2+1)\\ &=& (x+1)^2 \left[(2x-1)(1-x)(x^2+1) \right] \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f2a1f22e5f9d411bc55ea84ce43a6dad_l3.png)
Identifying ![]() , we find
, we find ![]() , which means the multiplicity of
, which means the multiplicity of ![]() is
is ![]() .
.
The zero ![]() came from the factor
came from the factor ![]() , so we have
, so we have
![]()
If we identify ![]() , we find
, we find ![]() so multiplicity here is
so multiplicity here is ![]() .
.
Last but not least, we turn our attention to our last zero, ![]() , which we obtained from solving
, which we obtained from solving ![]() . However, from
. However, from ![]() , we see the zero
, we see the zero ![]() corresponds to the factor
corresponds to the factor ![]() . We have
. We have
![]()
Identifying ![]() , we see
, we see ![]() , so the multiplicity
, so the multiplicity ![]() here as well.
here as well.
Example 2.2.3.2
Let ![]() . Describe the behavior of the graph of
. Describe the behavior of the graph of ![]() near each of the
near each of the ![]() -intercepts.
-intercepts.
Solution:
Describe the behavior of the graph of ![]() near each of the
near each of the ![]() -intercepts.
-intercepts.
From Theorem 2.6, because the multiplicities of ![]() and
and ![]() are both odd, we know the graph of
are both odd, we know the graph of ![]() crosses through the
crosses through the ![]() -axis at
-axis at ![]() and
and ![]() . More specifically, due to the fact that the multiplicity for both of these zeros is
. More specifically, due to the fact that the multiplicity for both of these zeros is ![]() , the graph will look locally linear at these points.
, the graph will look locally linear at these points.
Based on our calculations above, near ![]() , the graph will resemble the increasing line
, the graph will resemble the increasing line ![]() , and near
, and near ![]() , the graph will resemble the decreasing line
, the graph will resemble the decreasing line ![]() .
.
As the multiplicity of ![]() is even, we know the graph of
is even, we know the graph of ![]() touches and rebounds at
touches and rebounds at ![]() . The multiplicity of
. The multiplicity of ![]() is
is ![]() , thus the rebound will look locally like a parabola. More specifically, the graph near
, thus the rebound will look locally like a parabola. More specifically, the graph near ![]() will resemble
will resemble ![]() .
.
Example 2.2.3.3
Let ![]() . Determine the end behavior and
. Determine the end behavior and ![]() -intercept of the graph of
-intercept of the graph of ![]() .
.
Solution:
Determine the end behavior and ![]() -intercept of the graph of
-intercept of the graph of ![]() .
.
Per Theorem 2.4, the end behavior of ![]() , matches the end behavior of its leading term. As in Example 2.2.2, we multiply the leading terms from each factor together to obtain the leading term for
, matches the end behavior of its leading term. As in Example 2.2.2, we multiply the leading terms from each factor together to obtain the leading term for ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} p(x) &=& (2x-1)(x+1)(1-x^4) \\ &=& (2x)(x)(-x^4) + \ldots \\ &=& -2x^6 + \ldots \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-630cc02dec93e753848eded0360ef718_l3.png)
The degree here, ![]() , is even and the leading coefficient
, is even and the leading coefficient ![]() , so we know as
, so we know as ![]() ,
, ![]() .
.
To find the ![]() -intercept, we determine
-intercept, we determine ![]() , hence, the
, hence, the ![]() -intercept is
-intercept is ![]()
Example 2.2.3.4
Let ![]() . Sketch
. Sketch ![]() .
.
Solution:
Sketch ![]() .
.
From the end behavior, ![]() ,
, ![]() , we start the graph in Quadrant III and head towards
, we start the graph in Quadrant III and head towards ![]() .
.
At ![]() , we `bounce’ off of the
, we `bounce’ off of the ![]() -axis and head towards the
-axis and head towards the ![]() -intercept,
-intercept, ![]() .
.
We then head towards ![]() and cross through the
and cross through the ![]() -axis there.
-axis there.
Finally, we head back to the ![]() -axis and cross through at
-axis and cross through at ![]() .
.
Owing to the end behavior ![]() ,
, ![]() , we exit the picture in Quadrant IV.
, we exit the picture in Quadrant IV.
Remember polynomial functions are continuous and smooth, thus we have no holes or gaps in the graph, and all the `turns’ are rounded (no abrupt turns or corners.) We produce something resembling the next graph.
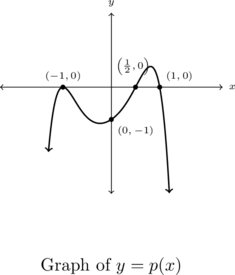
A couple of remarks about Example 2.2.3 are in order. First, notice that the factor ![]() was more of a spectator in our discussion of the zeros of
was more of a spectator in our discussion of the zeros of ![]() . Indeed, if we set
. Indeed, if we set ![]() , we have
, we have ![]() which provides no real solutions.[17] That being said, the factor
which provides no real solutions.[17] That being said, the factor ![]() does affect the shape of the graph. Next, when connecting up the graph from
does affect the shape of the graph. Next, when connecting up the graph from ![]() to
to ![]() to
to ![]() , there really is no way for us to know how low the graph goes, or where the lowest point is between
, there really is no way for us to know how low the graph goes, or where the lowest point is between ![]() and
and ![]() unless we plot more points. Likewise, we have no idea how high the graph gets between
unless we plot more points. Likewise, we have no idea how high the graph gets between ![]() and
and ![]() . While there are ways to determine these points analytically, more often than not, finding them requires Calculus. As these points do play an important role in many applications, we’ll need to discuss them in this course and, when required, we’ll use technology to find them. For that reason, we have the following definition:
. While there are ways to determine these points analytically, more often than not, finding them requires Calculus. As these points do play an important role in many applications, we’ll need to discuss them in this course and, when required, we’ll use technology to find them. For that reason, we have the following definition:
Definition 2.10
Suppose ![]() is a function with
is a function with ![]() .
.
- We say
 has a local minimum at the point
has a local minimum at the point 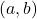 if and only if there is an open interval
if and only if there is an open interval 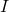 containing
containing  for which
for which 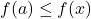 for all
for all  in
in 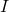 . The value
. The value 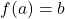 is called `a local minimum value of
is called `a local minimum value of  .’ That is,
.’ That is,  is the minimum
is the minimum  value over an open interval containing
value over an open interval containing  . Graphically, no points `near’ a local minimum are lower than
. Graphically, no points `near’ a local minimum are lower than 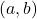 .
. - We say
 has a local maximum at the point
has a local maximum at the point 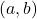 if and only if there is an open interval
if and only if there is an open interval  containing
containing  for which
for which 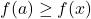 for all
for all  in
in  . The value
. The value  is called `a local maximum value of
is called `a local maximum value of  .’ That is,
.’ That is,  is the maximum
is the maximum  value over an open interval containing
value over an open interval containing  . Graphically, no points `near’ a local maximum are higher than
. Graphically, no points `near’ a local maximum are higher than  .
.
Taken together, the local maximums and local minimums of a function, if they exist, are called the local extrema of the function.
Once again, the terminology used in Definition 2.10 blurs the line between the function ![]() and its outputs,
and its outputs, ![]() . Also, some textbooks use the terms `relative’ minimum and `relative’ maximum instead of the adjective `local.’ Lastly, note the definition of local extrema requires an open interval exist in the domain containing
. Also, some textbooks use the terms `relative’ minimum and `relative’ maximum instead of the adjective `local.’ Lastly, note the definition of local extrema requires an open interval exist in the domain containing ![]() in order for
in order for ![]() to be a candidate for a local maximum or local minimum. We’ll have more to say about this in later chapters. If our open interval happens to be
to be a candidate for a local maximum or local minimum. We’ll have more to say about this in later chapters. If our open interval happens to be ![]() , then our local extrema are the extrema of
, then our local extrema are the extrema of ![]() – we’ll see an example of this momentarily.
– we’ll see an example of this momentarily.
Below we use a graphing utility to graph ![]() . We first consider the point
. We first consider the point ![]() . Even though there are points on the graph of
. Even though there are points on the graph of ![]() that are higher than
that are higher than ![]() , locally,
, locally, ![]() is the top of a hill. To satisfy Definition 2.10, we need to provide an open interval on which
is the top of a hill. To satisfy Definition 2.10, we need to provide an open interval on which ![]() is the largest, or maximum function value. Note the definition requires us to provide \textit{just one} open interval. One that works is the interval
is the largest, or maximum function value. Note the definition requires us to provide \textit{just one} open interval. One that works is the interval ![]() . We could use any smaller interval or go as large as
. We could use any smaller interval or go as large as ![]() (can you see why?) Next we encounter a `low’ point at approximately
(can you see why?) Next we encounter a `low’ point at approximately ![]() . More specifically, for all
. More specifically, for all ![]() in the interval, say,
in the interval, say, ![]() ,
, ![]() , Hence, we have a local minimum at
, Hence, we have a local minimum at ![]() . Lastly, at
. Lastly, at ![]() , we are back to a high point. In fact,
, we are back to a high point. In fact, ![]() isn’t just a local maximum value, based on the graph, it is the maximum of
isn’t just a local maximum value, based on the graph, it is the maximum of ![]() . Here, we may choose the open interval
. Here, we may choose the open interval ![]() as the open interval required by Definition 2.10, because for all
as the open interval required by Definition 2.10, because for all ![]() ,
, ![]() . It is important to note that there is no minimum value of
. It is important to note that there is no minimum value of ![]() despite there being a local minimum value.[18]
despite there being a local minimum value.[18]
We close this section with a classic application of a third degree polynomial function.
Example 2.2.4
Example 2.2.4.1
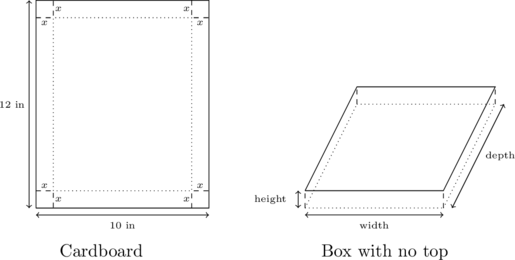
A box with no top is to be fashioned from a ![]() inch
inch ![]()
![]() inch piece of cardboard by cutting out congruent squares from each corner of the cardboard and then folding the resulting tabs. Let
inch piece of cardboard by cutting out congruent squares from each corner of the cardboard and then folding the resulting tabs. Let ![]() denote the length of the side of the square which is removed from each corner.
denote the length of the side of the square which is removed from each corner.
Write an expression for ![]() , the volume of the box produced by removing squares of edge length
, the volume of the box produced by removing squares of edge length ![]() . Include an appropriate domain.
. Include an appropriate domain.
Solution:
Write an expression for ![]() , the volume of the box produced by removing squares of edge length
, the volume of the box produced by removing squares of edge length ![]() . Include an appropriate domain.
. Include an appropriate domain.
From Geometry, we know that Volume = width ![]() height
height ![]() depth. The key is to find each of these quantities in terms of
depth. The key is to find each of these quantities in terms of ![]() . From the figure, we see that the height of the box is
. From the figure, we see that the height of the box is ![]() itself. The cardboard piece is initially
itself. The cardboard piece is initially ![]() inches wide. Removing squares with a side length of
inches wide. Removing squares with a side length of ![]() inches from each corner leaves
inches from each corner leaves ![]() inches for the width.[19] As for the depth, the cardboard is initially
inches for the width.[19] As for the depth, the cardboard is initially ![]() inches long, so after cutting out
inches long, so after cutting out ![]() inches from each side, we would have
inches from each side, we would have ![]() inches remaining. Hence, we get
inches remaining. Hence, we get
![]()
To find a suitable applied domain, we note that to make a box at all we need ![]() . Also the shorter of the two dimensions of the cardboard is
. Also the shorter of the two dimensions of the cardboard is ![]() inches, and as we are removing
inches, and as we are removing ![]() inches from this dimension, we also require
inches from this dimension, we also require ![]() or
or ![]() . Hence, our applied domain is
. Hence, our applied domain is ![]() .
.
Example 2.2.4.2
A box with no top is to be fashioned from a ![]() inch
inch ![]()
![]() inch piece of cardboard by cutting out congruent squares from each corner of the cardboard and then folding the resulting tabs. Let
inch piece of cardboard by cutting out congruent squares from each corner of the cardboard and then folding the resulting tabs. Let ![]() denote the length of the side of the square which is removed from each corner.
denote the length of the side of the square which is removed from each corner.

Use a graphing utility to help you determine the value of ![]() which produces the box with the largest volume. What is the largest volume? Round your answers to two decimal places.
which produces the box with the largest volume. What is the largest volume? Round your answers to two decimal places.
Solution:
Use a graphing utility to help you determine the value of ![]() which produces the box with the largest volume. What is the largest volume? Round your answers to two decimal places.
which produces the box with the largest volume. What is the largest volume? Round your answers to two decimal places.
Using a graph and technology, we identify a local maximum at approximately ![]() . Because the domain of
. Because the domain of ![]() is restricted to the interval
is restricted to the interval ![]() , the maximum of
, the maximum of ![]() is here as well.
is here as well.
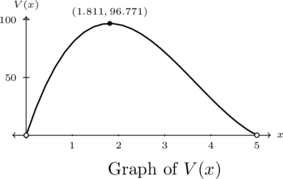
This means the maximum volume attainable is approximately 96.77 cubic inches when we remove squares of approximately 1.81 inches per side.
Notice that there is a very slight, but important, difference between the function ![]() ,
, ![]() from Example 2.2.4 and the function
from Example 2.2.4 and the function ![]() : their domains. The domain of
: their domains. The domain of ![]() is restricted to the interval
is restricted to the interval ![]() while the domain of
while the domain of ![]() is
is ![]() . Indeed, the function
. Indeed, the function ![]() has a maximum of (approximately) 96.771 at (approximately) x = 1.811 whereas for the function
has a maximum of (approximately) 96.771 at (approximately) x = 1.811 whereas for the function ![]() , 96.771 is a local maximum value only. We leave it to the reader to verify that
, 96.771 is a local maximum value only. We leave it to the reader to verify that ![]() has neither a minimum nor a local minimum.
has neither a minimum nor a local minimum.
2.2.3 Section Exercises
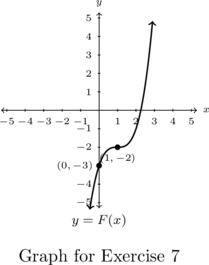
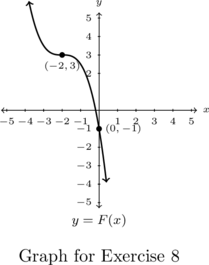
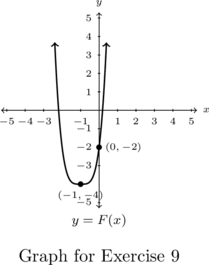
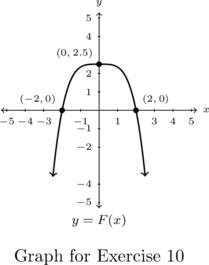
In Exercises 1 – 6, given the pair of functions ![]() and
and ![]() , sketch the graph of
, sketch the graph of ![]() by starting with the graph of
by starting with the graph of ![]() and using Theorem 2.2. Track at least three points of your choice through the transformations. State the domain and range of
and using Theorem 2.2. Track at least three points of your choice through the transformations. State the domain and range of ![]() .
.
 and
and 
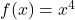 and
and 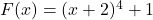
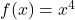 and
and 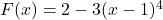
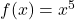 and
and 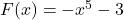
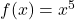 and
and 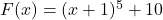
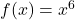 and
and 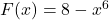
In Exercises 7 – 8, find a formula for each function below in the form ![]() .
.
In Exercises 9 – 10, find a formula for each function below in the form ![]() .
.
In Exercises 11 – 20, find the degree, the leading term, the leading coefficient, the constant term and the end behavior of the given polynomial function.
In Exercises 21 – 30, find the real zeros of the given polynomial and their corresponding multiplicities. Use this information along with end behavior to provide a rough sketch of the graph of the polynomial function.
In Exercises 31 – 45, determine analytically if the following functions are even, odd or neither.
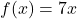
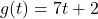
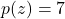
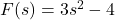
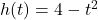
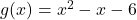
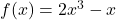
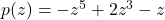
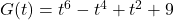
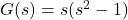
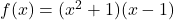
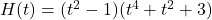
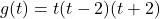
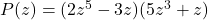
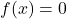
- Suppose
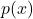 is a polynomial function written in the form of Definition 2.7.
is a polynomial function written in the form of Definition 2.7.
- If the nonzero terms of
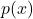 consist of even powers of
consist of even powers of  (or a constant), explain why
(or a constant), explain why 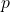 is even.
is even. - If the nonzero terms of
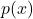 consist of odd powers of
consist of odd powers of  , explain why
, explain why 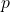 is odd.
is odd. - If
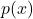 the nonzero terms of
the nonzero terms of 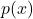 contain at least one odd power of
contain at least one odd power of  and one even power of
and one even power of  (or a constant term), then
(or a constant term), then 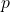 is neither even nor odd.
is neither even nor odd.
- If the nonzero terms of
- Use the results of Exercise 46 to determine whether the following functions are even, odd, or neither.
- Show
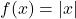 is an even function.
is an even function. - Rework Example 2.2.4 assuming the box is to be made from an 8.5 inch by 11 inch sheet of paper. Using scissors and tape, construct the box. Are you surprised?[20]
- For each function
 listed below, compute the average rate of change over the indicated interval.[21] What trends do you observe? How do your answers manifest themselves graphically?
listed below, compute the average rate of change over the indicated interval.[21] What trends do you observe? How do your answers manifest themselves graphically?
![Rendered by QuickLaTeX.com \[ \begin{array}{|r||c|c|c|c|c|c|} \hline f(x) & [-0.1, 0] & [0, 0.1] &[0.9, 1] & [1, 1.1] & [1.9, 2] & [2, 2.1] \\ \hline 1 &&&&&& \\ \hline x &&&&&& \\ \hline x^2 &&&&&& \\ \hline x^3 &&&&&& \\ \hline x^4 &&&&&& \\ \hline x^5 &&&&&& \\ \hline \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d21c4f348e70e7f71d71ac8841c8930a_l3.png)
- For each function
 listed below, compute the average rate of change over the indicated interval.[22] What trends do you observe? How do your answers manifest themselves graphically?
listed below, compute the average rate of change over the indicated interval.[22] What trends do you observe? How do your answers manifest themselves graphically?
![Rendered by QuickLaTeX.com \[ \begin{array}{|r||c|c|c|c|} \hline f(x) & [0.9, 1.1] & [0.99, 1.01] &[0.999, 1.001] & [0.9999, 1.0001] \\ \hline 1 &&&& \\ \hline x &&&& \\ \hline x^2 &&&& \\ \hline x^3 &&&& \\ \hline x^4 &&&& \\ \hline x^5 &&&& \\ \hline \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-432bcfffc27d2d8e715ecaf39e0b32a4_l3.png)
In Exercises 52 – 54, suppose the revenue ![]() , in \textit{thousands} of dollars, from producing and selling
, in \textit{thousands} of dollars, from producing and selling ![]() \textit{hundred} LCD TVs is given by
\textit{hundred} LCD TVs is given by ![]() for
for ![]() .
.
- Graph
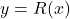 and determine the number of TVs which should be sold to maximize revenue. What is the maximum revenue?
and determine the number of TVs which should be sold to maximize revenue. What is the maximum revenue? - Assume the cost, in thousands of dollars, to produce
 hundred LCD TVs is given by the function
hundred LCD TVs is given by the function 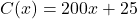 for
for 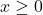 . Find and simplify an expression for the profit function
. Find and simplify an expression for the profit function 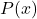 .(Remember: Profit = Revenue – Cost.)
.(Remember: Profit = Revenue – Cost.) - Graph
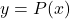 and determine the number of TVs which should be sold to maximize profit. What is the maximum profit?
and determine the number of TVs which should be sold to maximize profit. What is the maximum profit? - While developing their newest game, Sasquatch Attack!, the makers of the PortaBoy (from Example 1.3.8) revised their cost function and now use
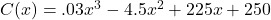 , for
, for 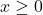 . As before,
. As before, 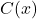 is the cost to make
is the cost to make  PortaBoy Game Systems. Market research indicates that the demand function
PortaBoy Game Systems. Market research indicates that the demand function 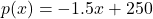 remains unchanged. Use a graphing utility to find the production level
remains unchanged. Use a graphing utility to find the production level  that maximizes the profit made by producing and selling
that maximizes the profit made by producing and selling  PortaBoy game systems.
PortaBoy game systems. - According to US Postal regulations, a rectangular shipping box must satisfy the following inequality: “Length + Girth
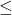 130 inches” for Parcel Post and “Length + Girth
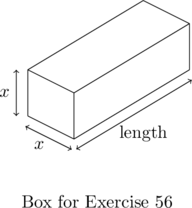
130 inches” for Parcel Post and “Length + Girth 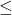 108 inches” for other services. Let’s assume we have a closed rectangular box with a square face of side length
108 inches” for other services. Let’s assume we have a closed rectangular box with a square face of side length  as drawn below. The length is the longest side and is clearly labeled. The girth is the distance around the box in the other two dimensions so in our case it is the sum of the four sides of the square,
as drawn below. The length is the longest side and is clearly labeled. The girth is the distance around the box in the other two dimensions so in our case it is the sum of the four sides of the square, 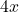 .
.
- Assuming that we’ll be mailing a box via Parcel Post where Length + Girth
 130 inches, express the length of the box in terms of
130 inches, express the length of the box in terms of  and then express the volume
and then express the volume 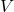 of the box in terms of
of the box in terms of  .
. - Find the dimensions of the box of maximum volume that can be shipped via Parcel Post.
- Repeat parts 56a and 56b if the box is shipped using “other services”.
- Assuming that we’ll be mailing a box via Parcel Post where Length + Girth
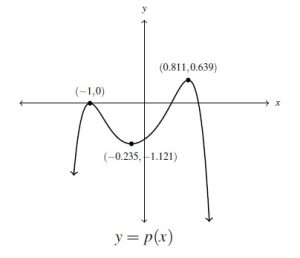
- Below is a graph of a polynomial function
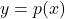 . Answer the following questions about
. Answer the following questions about  based on the graph provided.
based on the graph provided.
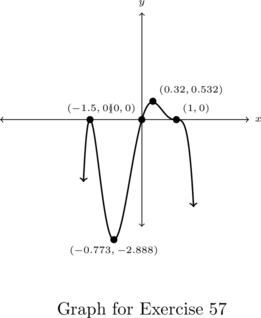
- Describe the end behavior of
 .
. - List the real zeros of
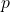 along with their respective multiplicities.
along with their respective multiplicities. - List the local minimums and local maximums of the graph of
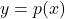 .
. - What can be said about the degree of and leading coefficient
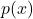 ?
? - It turns out that
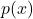 is a seventh degree polynomial.[23] How can this be?
is a seventh degree polynomial.[23] How can this be?
- Describe the end behavior of
- Use the graph of
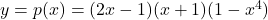 prior to Example 2.2.4 to estimate the largest open interval containing
prior to Example 2.2.4 to estimate the largest open interval containing 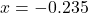 which satisfies the the criteria for `local minimum’ in Definition 2.10.
which satisfies the the criteria for `local minimum’ in Definition 2.10. - (This is a follow-up to Exercises 96 in Section 1.3.1 and 33 in Section 2.1.) The Lagrange Interpolate function
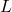 for four points:
for four points: 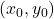 ,
, 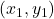 ,
, 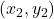 ,
, 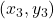 where
where 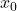 ,
, 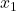 ,
, 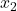 , and
, and 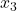 are four distinct real numbers is given by the formula:
are four distinct real numbers is given by the formula:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl}L(x) & = & y_{0} \dfrac{(x - x_{1}) (x - x_{2}) (x-x_{3})}{(x_{0} - x_{1})(x_{0} - x_{2})(x_{0} - x_{3})}+ y_{1} \dfrac{(x - x_{0}) (x - x_{2}) (x-x_{3})}{(x_{1} - x_{0})(x_{1} - x_{2})(x_{1} - x_{3})} \\ [15pt] && +y_{2} \dfrac{(x - x_{0}) (x - x_{1}) (x-x_{3})}{(x_{2} - x_{0})(x_{2} - x_{1})(x_{2} - x_{3})}+ y_{3} \dfrac{(x - x_{0}) (x - x_{1}) (x-x_{2})}{(x_{3} - x_{0})(x_{3} - x_{1})(x_{3} - x_{2})} \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b6fc7cbed8a58984f2977c36c0e0275c_l3.png)
- Choose four points with different
 -values and construct the Lagrange Interpolate for those points. Verify each of the points lies on the polynomial.
-values and construct the Lagrange Interpolate for those points. Verify each of the points lies on the polynomial. - Verify that, in general,
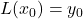 ,
, 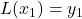 ,
, 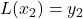 , and
, and 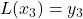 .
. - Find
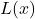 for the points
for the points 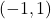 ,
, 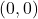 ,
, 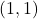 and
and 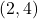 . What happens?
. What happens? - Find
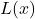 for the points
for the points 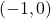 ,
, 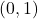 ,
, 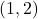 and
and 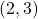 . What happens?
. What happens? - Generalize the formula for
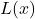 to five points. What’s the pattern?
to five points. What’s the pattern?
- Choose four points with different
Section 2.2 Exercise Answers can be found in the Appendix … Coming soon
- More specifically,
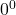 is an indeterminate form. These are studied extensively in Calculus. ↵
is an indeterminate form. These are studied extensively in Calculus. ↵ - This is why we do not describe monomial functions as having the form
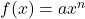 for any whole number
for any whole number 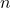 . See Section 0.1.1. ↵
. See Section 0.1.1. ↵ - Recall that
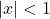 is equivalent to
is equivalent to 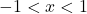 and
and 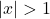 is equivalent to
is equivalent to 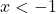 or
or 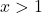 . Using absolute values allow us to describe these sets of real numbers more succinctly. ↵
. Using absolute values allow us to describe these sets of real numbers more succinctly. ↵ - This should sound familiar - see the comments regarding the range of
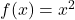 in Section 2.1. ↵
in Section 2.1. ↵ - Do you see the importance of
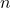 being odd here? ↵
being odd here? ↵ - We are using the dummy variable
 here instead of
here instead of  for reasons that will become apparent shortly. ↵
for reasons that will become apparent shortly. ↵ - That is, for a fixed number
 every real number
every real number  can be written as
can be written as 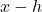 for some real number
for some real number  , and every real number
, and every real number  can be written as
can be written as 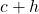 for some real number
for some real number  . ↵
. ↵ - Sometimes called the `long run' behavior. ↵
- said differently, negative values that are larger in absolute value ↵
- That is, the
 values grow larger than any positive number. They are `unbounded.' ↵
values grow larger than any positive number. They are `unbounded.' ↵ - Some authors say
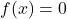 has degree
has degree  for reasons not even we will go into. ↵
for reasons not even we will go into. ↵ - We are considering
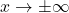 , thus we are not concerned with
, thus we are not concerned with  even being close to
even being close to  , so these fractions will all be defined. ↵
, so these fractions will all be defined. ↵ - Or at least they appear to within the limits of the technology. ↵
- Both of which, by the way, can lead one astray, so we must proceed cautiously. ↵
- Again, the formal definition of `continuity' and properties of continuous functions are discussed in Calculus. ↵
- in accordance with the Zero Product Property of the Real Numbers - see Section 0.1. ↵
- The solutions are
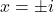 - see Section 0.5.6. ↵
- see Section 0.5.6. ↵ - Some books use the adjectives `global' or `absolute' when describing the extreme values of a function to distinguish them from their local counterparts. ↵
- There's no harm in taking an extra step here and making sure this makes sense. If we chopped out a
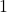 inch square from each side, then the width would be
inch square from each side, then the width would be  inches, so chopping out
inches, so chopping out  inches would leave
inches would leave 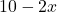 inches. ↵
inches. ↵ - Consider decorating the box and presenting it to your instructor. If done well enough, maybe your instructor will issue you some bonus points. Or maybe not. ↵
- See Definition 1.11 in Section 1.3.4 for a review of this concept, as needed. ↵
- See Definition 1.11 in Section 1.3.4 for a review of this concept, as needed. ↵
- to be exact,
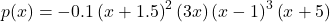 . ↵
. ↵
A constant function or a function of the form x raised to a natural number.
A function is even if f(-x)=f(x) for all x in the domain of f.
A function is odd if f(-x)=-f(x) for all x in the domain of f.
A function with the sum or difference between terms of x raised to whole number powers.
The degree of a polynomial is the largest natural number the variable of the polynomial is raised to.
The leading term of a polynomial is the term containing the largest natural number power.
The leading coefficient of a polynomial is the coefficient of the leading term.
The term of a polynomial with the variable raised to the 0 power or the term with only a constant and no variable.
The multiplicity of a zero is the number of times the zero occurs for a function.