3.2 Properties of Rational Functions
If we add, subtract, or multiply polynomial functions, the result is another polynomial function. When we divide polynomial functions, however, we may not get a polynomial function. The result of dividing two polynomials is a rational function, so named because rational functions are ratio of polynomials.
Definition 3.1
A rational function is a function which is the ratio of polynomial functions. Said differently, ![]() is a rational function if it is of the form
is a rational function if it is of the form
![]()
where ![]() and
and ![]() are polynomial functions.[1]
are polynomial functions.[1]
3.2.1 Laurent Monomial Functions
As with polynomial functions, we begin our study of rational functions with what are, in some sense, the building blocks of rational functions, Laurent monomial functions.
Definition 3.2
A Laurent monomial function is either a monomial function (see Definition 2.4) or a function of the form ![]() for
for ![]() .
.
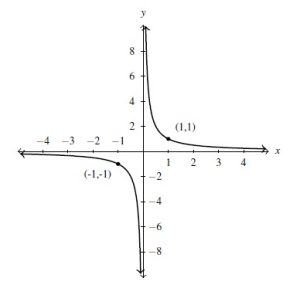
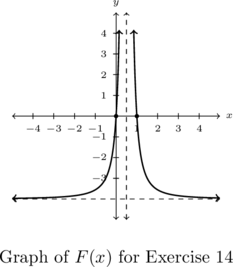
Laurent monomial functions are named in honor of Pierre Alphonse Laurent and generalize the notion of `monomial function’ from Chapter 2 to terms with negative exponents. Our study of these functions begins with an analysis of ![]() , the reciprocal function. The first item worth noting is that
, the reciprocal function. The first item worth noting is that ![]() is not defined owing to the presence of
is not defined owing to the presence of ![]() in the denominator. That is, the domain of
in the denominator. That is, the domain of ![]() is
is ![]() or, using interval notation,
or, using interval notation, ![]() . Of course excluding
. Of course excluding ![]() from the domain of
from the domain of ![]() serves only to pique our curiosity about the behavior of
serves only to pique our curiosity about the behavior of ![]() when
when ![]() . Thinking from a number sense perspective, the closer the denominator of
. Thinking from a number sense perspective, the closer the denominator of ![]() is to
is to ![]() , the larger the value of the fraction (in absolute value.)[2] So it stands to reason that as
, the larger the value of the fraction (in absolute value.)[2] So it stands to reason that as ![]() gets closer and closer to
gets closer and closer to ![]() , the values for
, the values for ![]() should grow larger and larger (in absolute value.) This is borne out in the table on the left where it is apparent that for
should grow larger and larger (in absolute value.) This is borne out in the table on the left where it is apparent that for ![]() ,
, ![]() is becoming unbounded.
is becoming unbounded.
As we investigate the end behavior of ![]() , we find that as
, we find that as ![]() ,
, ![]() . Again, number sense agrees here with the data, because as the denominator of
. Again, number sense agrees here with the data, because as the denominator of ![]() becomes unbounded, the value of the fraction should diminish. That being said, we could ask if the graph ever reaches the
becomes unbounded, the value of the fraction should diminish. That being said, we could ask if the graph ever reaches the ![]() -axis. If we attempt to solve
-axis. If we attempt to solve ![]() . we arrive at the contradiction
. we arrive at the contradiction ![]() hence,
hence, ![]() is not in the range of
is not in the range of ![]() . Every other real number besides
. Every other real number besides ![]() is in the range of
is in the range of ![]() , however. To see this, let
, however. To see this, let ![]() be a real number. Then
be a real number. Then ![]() is defined and, moreover,
is defined and, moreover, ![]() . This shows
. This shows ![]() is in the range of
is in the range of ![]() . Hence, the range of
. Hence, the range of ![]() is
is ![]() or, using interval notation,
or, using interval notation, ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{array}{ccc} \begin{array}{|r||c|} \hline x & r(x) = \frac{1}{x} \\ \hline -0.01& -100 \\ \hline -0.001 & -1000 \\ \hline -0.0001 & -10000 \\ \hline -0.00001 & -100000 \\ \hline 0 & \text{undefined} \\ \hline 0.00001 & 100000 \\ \hline 0.0001 & 10000 \\ \hline 0.001 & 1000 \\ \hline 0.01 & 100 \\ \hline \end{array} & \hspace{1in} & \begin{array}{|r||c|} \hline x & r(x) = \frac{1}{x} \\ \hline -100000 & -0.00001 \\ \hline -10000 & -0.0001 \\ \hline -1000 & -0.001 \\ \hline -100 & -0.01 \\ \hline 0 & \text{undefined} \\ \hline 100 & 0.01 \\ \hline 1000 & 0.001 \\ \hline 10000 & 0.0001 \\ \hline 100000 & 0.00001 \\ \hline \end{array} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7bc3d8e8f10f6e4a403d843406d71d42_l3.png)
In order to more precisely describe the behavior near ![]() , we say `as
, we say `as ![]() approaches 0 from the left,’ written as
approaches 0 from the left,’ written as ![]() , the function values
, the function values ![]() . By `from the left’ we mean we are considering
. By `from the left’ we mean we are considering ![]() -values slightly to the left of
-values slightly to the left of ![]() on the number line, such as
on the number line, such as ![]() and
and ![]() in the table above. If we think of these numbers as all being
in the table above. If we think of these numbers as all being ![]() -values where
-values where ![]() `0
`0![]() a little bit’, then the `
a little bit’, then the `![]() ‘ in the notation `
‘ in the notation `![]() ‘ makes better sense. The notation to describe the
‘ makes better sense. The notation to describe the ![]() values,
values, ![]() , is used here in the same manner as it was in Section 2.2. That is, as
, is used here in the same manner as it was in Section 2.2. That is, as ![]() , the values
, the values ![]() are becoming unbounded in the negative direction.
are becoming unbounded in the negative direction.
Similarly, we say `as ![]() approaches
approaches ![]() from the right,’ that is as
from the right,’ that is as ![]() ,
, ![]() . Here `from the right’ means we are using
. Here `from the right’ means we are using ![]() values slightly to the right of
values slightly to the right of ![]() on the number line: numbers such as
on the number line: numbers such as ![]() which could be described as `
which could be described as `![]() a little bit.’ For these values of
a little bit.’ For these values of ![]() , the values of
, the values of ![]() become unbounded (in the positive direction) so we write
become unbounded (in the positive direction) so we write ![]() here.
here.
We can also use this notation to describe the end behavior, but here the numerical roles are reversed. We see as ![]() ,
, ![]() and as
and as ![]() ,
, ![]() .
.
The way we describe what is happening graphically is to say the line ![]() is a vertical asymptote of the graph of
is a vertical asymptote of the graph of ![]() an the line
an the line ![]() is a horizontal asymptote of the graph of
is a horizontal asymptote of the graph of ![]() . Roughly speaking, asymptotes are lines which approximate functions as either the inputs or outputs become unbounded. While defined more precisely using the language of Calculus, we will do our best to formally define vertical and horizontal asymptotes below.
. Roughly speaking, asymptotes are lines which approximate functions as either the inputs or outputs become unbounded. While defined more precisely using the language of Calculus, we will do our best to formally define vertical and horizontal asymptotes below.
Definition 3.3
The line ![]() is called a vertical asymptote of the graph of a function
is called a vertical asymptote of the graph of a function ![]() if as
if as ![]() or as
or as ![]() , either
, either ![]() or
or ![]() .
.
Definition 3.4
The line ![]() is called a horizontal asymptote of the graph of a function
is called a horizontal asymptote of the graph of a function ![]() if as
if as ![]() or as
or as ![]() ,
, ![]() .
.
Note that in Definition3.4, we write ![]() (not
(not ![]() or
or ![]() ) because we are unconcerned from which direction the values
) because we are unconcerned from which direction the values ![]() approach the value
approach the value ![]() , just as long as they do so. As we shall see, the graphs of rational functions may, in fact, cross their horizontal asymptotes. If this happens, however, it does so only a finite number of times (at least in this chapter), and so for each choice of
, just as long as they do so. As we shall see, the graphs of rational functions may, in fact, cross their horizontal asymptotes. If this happens, however, it does so only a finite number of times (at least in this chapter), and so for each choice of ![]() and
and ![]() ,
, ![]() will approach
will approach ![]() from either below (in the case
from either below (in the case ![]() ) or above (in the case
) or above (in the case ![]() .) We leave
.) We leave ![]() generic in our definition, however, to allow this concept to apply to less tame specimens in the Precalculus zoo, one that cross horizontal asymptotes an infinite number of times.[3]
generic in our definition, however, to allow this concept to apply to less tame specimens in the Precalculus zoo, one that cross horizontal asymptotes an infinite number of times.[3]
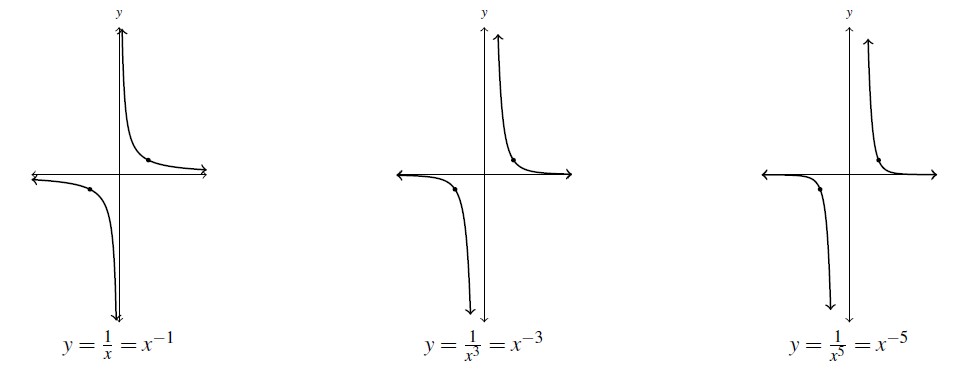
The behaviors illustrated in the graph ![]() are typical of functions of the form
are typical of functions of the form ![]() for natural numbers,
for natural numbers, ![]() . As with the monomial functions discussed in Section 2.2 the patterns that develop primarily depend on whether
. As with the monomial functions discussed in Section 2.2 the patterns that develop primarily depend on whether ![]() is odd or even. Having thoroughly discussed the graph of
is odd or even. Having thoroughly discussed the graph of ![]() , we graph it along with
, we graph it along with ![]() and
and ![]() below. Note the points
below. Note the points ![]() and
and ![]() are common to all three graphs as are the asymptotes
are common to all three graphs as are the asymptotes ![]() and
and ![]() . As the
. As the ![]() increases, the graphs become steeper for
increases, the graphs become steeper for ![]() and flatten out more quickly for
and flatten out more quickly for ![]() . Both the domain and range in each case appears to be
. Both the domain and range in each case appears to be ![]() . Indeed, owing to the
. Indeed, owing to the ![]() in the denominator of
in the denominator of ![]() ,
, ![]() , and only
, and only ![]() , is undefined. Hence the domain is
, is undefined. Hence the domain is ![]() . When thinking about the range, note the equation
. When thinking about the range, note the equation ![]() has the solution
has the solution ![]() as long as
as long as ![]() . This means
. This means ![]() for every nonzero real number
for every nonzero real number ![]() . If
. If ![]() , we are in the same situation as before:
, we are in the same situation as before: ![]() has no real solution. This establishes the range is
has no real solution. This establishes the range is ![]() . Finally, each of the graphs appear to be symmetric about the origin. Indeed, for odd
. Finally, each of the graphs appear to be symmetric about the origin. Indeed, for odd ![]() ,
, ![]() , proving every member of this function family is odd.
, proving every member of this function family is odd.
![Rendered by QuickLaTeX.com \[\begin{array}{|r||c|c|c|} \hline x & \frac{1}{x} = x^{-1} & \frac{1}{x^3} = x^{-3} & \frac{1}{x^5} = x^{-5} \\ \hline -10 & -0.1 &-0.001& -0.00001 \\ \hline -1 & -1 & -1& -1\\ \hline -0.1 & -10 & -1000& -100000 \\ \hline 0 & \text{undefined} & \text{undefined} & \text{undefined} \\ \hline 0.1 & 10 & 1000& 100000 \\ \hline 1 & 1 & 1& 1\\ \hline 10 & 0.1 & 0.001& 0.00001 \\ \hline \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-8a7c4facabb7967b252e32068ab9a141_l3.png)
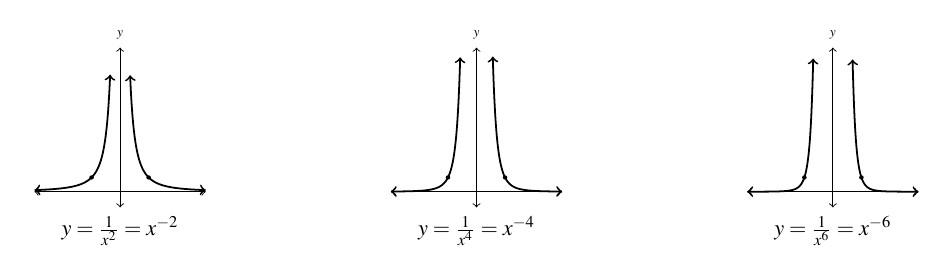
We repeat the same experiment with functions of the form ![]() where
where ![]() is even.
is even. ![]() ,
, ![]() and
and ![]() . These graphs all share the points
. These graphs all share the points ![]() and
and ![]() , and asymptotes
, and asymptotes ![]() and
and ![]() . The same remarks about the steepness for
. The same remarks about the steepness for ![]() and the flattening for
and the flattening for ![]() also apply. For the same reasons as given above, the domain of each of these functions is
also apply. For the same reasons as given above, the domain of each of these functions is ![]() . When it comes to the range, the fact
. When it comes to the range, the fact ![]() is even tells us there are solutions to
is even tells us there are solutions to ![]() only if
only if ![]() . It follows that the range is
. It follows that the range is ![]() for each of these functions. Concerning symmetry, as
for each of these functions. Concerning symmetry, as ![]() is even,
is even, ![]() , proving each member of this function family is even. Hence, all of the graphs of these functions is symmetric about the
, proving each member of this function family is even. Hence, all of the graphs of these functions is symmetric about the ![]() -axis.
-axis.
![Rendered by QuickLaTeX.com \[\begin{array}{|r||c|c|c|} \hline x & \frac{1}{x^2} = x^{-2} & \frac{1}{x^4} = x^{-4} & \frac{1}{x^6} = x^{-6} \\[2pt] \hline -10 &0.01 &0.0001& 1 \times 10^{-6} \\ \hline -1 & 1 & 1& 1\\ \hline -0.1 & 100 & 10000 & 1 \times 10^{6} \\ \hline 0 & \text{undefined} & \text{undefined} & \text{undefined} \\ \hline 0.1 & 100 & 10000 & 1 \times 10^{6} \\ \hline 1& 1 & 1& 1 \\ \hline 10 &0.01 &0.0001& 1 \times 10^{-6} \\ \hline \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-730022c633f4d459ddadd3b72e7970a3_l3.png)
Not surprisingly, we have an analog to Theorem 2.2 for this family of Laurent monomial functions.
Theorem 3.1
For real numbers ![]() ,
, ![]() , and
, and ![]() with
with ![]() , the graph of
, the graph of ![]() can be obtained from the graph of
can be obtained from the graph of ![]() by performing the following operations, in sequence:
by performing the following operations, in sequence:
- add
 to each of the
to each of the  -coordinates of the points on the graph of
-coordinates of the points on the graph of  . This results in a horizontal shift to the right if
. This results in a horizontal shift to the right if 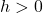 or left if
or left if 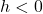 .
.
NOTE: This transforms the graph of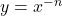 to
to 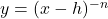 .
.
The vertical asymptote moves from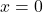 to
to 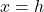 .
. - multiply the
 -coordinates of the points on the graph obtained in Step 1 by
-coordinates of the points on the graph obtained in Step 1 by  . This results in a vertical scaling, but may also include a reflection about the
. This results in a vertical scaling, but may also include a reflection about the  -axis if
-axis if 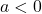 .
.
NOTE: This transforms the graph of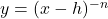 to
to 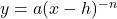 .
. - add
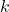 to each of the
to each of the  -coordinates of the points on the graph obtained in Step 2. This results in a vertical shift up if
-coordinates of the points on the graph obtained in Step 2. This results in a vertical shift up if 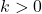 or down if
or down if 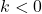 .
.
NOTE: This transforms the graph of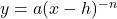 to
to 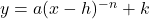 .
.
The horizontal asymptote moves from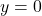 to
to 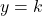 .
.
The proof of Theorem 3.1 is identical to the proof of Theorem 2.2 – just replace ![]() with
with ![]() . We nevertheless encourage the reader to work through the details[4] and compare the results of this theorem with Theorems 1.4, 2.1, and 2.2.
. We nevertheless encourage the reader to work through the details[4] and compare the results of this theorem with Theorems 1.4, 2.1, and 2.2.
We put Theorem 3.1 to good use in the following example.
Example 3.2.1
Example 3.2.1.1
Use Theorem 3.1 to graph the following. Label at least two points and the asymptotes. State the domain and range using interval notation.
![]()
Solution:
Graph ![]() .
.
In order to use Theorem 3.1, we first must put ![]() into the form prescribed by the theorem. To that end, we factor:
into the form prescribed by the theorem. To that end, we factor:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} f(x) &=& \left(2 \left[x - \frac{3}{2} \right] \right)^{-2} \\[6pt] &=& 2^{-2} \left(x - \frac{3}{2} \right)^{-2} \\[6pt] &=& \frac{1}{4} \left(x - \frac{3}{2} \right)^{-2} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9c46cf6c0eb04786f3728438e0dcc327_l3.png)
We identify ![]() ,
, ![]() and
and ![]() (and
(and ![]() .) Per the theorem, we begin with the graph of
.) Per the theorem, we begin with the graph of ![]() and track the two points
and track the two points ![]() and
and ![]() along with the vertical and horizontal asymptotes
along with the vertical and horizontal asymptotes ![]() and
and ![]() , respectively through each step.
, respectively through each step.
Step 1: add ![]() to each of the
to each of the ![]() -coordinates of each of the points on the graph of
-coordinates of each of the points on the graph of ![]() . This moves the vertical asymptote from
. This moves the vertical asymptote from ![]() to
to ![]() (which we represent by a dashed line.)
(which we represent by a dashed line.)

Step 2: multiply each of the ![]() -coordinates of each of the points on the graph of
-coordinates of each of the points on the graph of ![]() by
by ![]() .
.

As we did not shift the graph vertically, the horizontal asymptote remains ![]() . We can determine the domain and range of
. We can determine the domain and range of ![]() by tracking the changes to the domain and range of our progenitor function,
by tracking the changes to the domain and range of our progenitor function, ![]() .
.
We get the domain and range of ![]() is
is ![]() and the range of
and the range of ![]() is
is ![]() .
.
Example 3.2.1.2
Use Theorem 3.1 to graph the following. Label at least two points and the asymptotes. State the domain and range using interval notation.
![]()
Solution:
Graph ![]() .
.
Using long division, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(t) &=& \frac{2t-1}{t+1} \\[10pt] &=& - \frac{3}{t+1} + 2 \\[10pt] &=& \frac{-3}{(t-(-1))^{1}} + 2 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-2f4279789dd96560eaa02908d4cf9271_l3.png)
so we identify ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
We start with the graph of ![]() with points
with points ![]() ,
, ![]() and asymptotes
and asymptotes ![]() and
and ![]() and track these through each of the steps.
and track these through each of the steps.
Step 1: Add ![]() to each of the
to each of the ![]() -coordinates of each of the points on the graph of
-coordinates of each of the points on the graph of ![]() . This moves the vertical asymptote from
. This moves the vertical asymptote from ![]() to
to ![]() .
.

Step 2: multiply each of the ![]() -coordinates of each of the points on the graph of
-coordinates of each of the points on the graph of ![]() by
by ![]() .
.

Step 3: add ![]() to each of the
to each of the ![]() -coordinates of each of the points on the graph of
-coordinates of each of the points on the graph of ![]() . This moves the horizontal asymptote from
. This moves the horizontal asymptote from ![]() to
to ![]() .
.

As above, we determine the domain and range of ![]() by tracking the changes in the domain and range of
by tracking the changes in the domain and range of ![]() . We find the domain of
. We find the domain of ![]() is
is ![]() and the range is
and the range is ![]() .
.
In Example 3.2.1, we once again see the benefit of changing the form of a function to make use of an important result. A natural question to ask is to what extent general rational functions can be rewritten to use Theorem 3.1. In the same way polynomial functions are sums of monomial functions, it turns out, allowing for non-real number coefficients, that every rational function can be written as a sum of (possibly shifted) Laurent monomial functions.
3.2.2 Local Behavior Near Excluded Values
We take time now to focus on behaviors of the graphs of rational functions near excluded values. We’ve already seen examples of one type of behavior: vertical asymptotes. Our next example gives us a physical interpretation of a vertical asymptote. This type of model arises from a family of equations cheerily named `doomsday’ equations.[5]
Example 3.2.2
Example 3.2.2.1
A mathematical model for the population ![]() , in thousands, of a certain species of bacteria,
, in thousands, of a certain species of bacteria, ![]() days after it is introduced to an environment is given by
days after it is introduced to an environment is given by ![]() ,
, ![]() .
.
Compute and interpret ![]() .
.
Solution:
Compute and interpret ![]() .
.
Substituting ![]() gives
gives ![]() .
.
Due to the fact that ![]() represents the number of days after the bacteria are introduced into the environment,
represents the number of days after the bacteria are introduced into the environment, ![]() corresponds to the day the bacteria are introduced.
corresponds to the day the bacteria are introduced. ![]() is measured in thousands, thus
is measured in thousands, thus ![]() means
means ![]() bacteria are initially introduced into the environment.
bacteria are initially introduced into the environment.
Example 3.2.2.2
A mathematical model for the population ![]() , in thousands, of a certain species of bacteria,
, in thousands, of a certain species of bacteria, ![]() days after it is introduced to an environment is given by
days after it is introduced to an environment is given by ![]() ,
, ![]() .
.
When will the population reach 100,000?
Solution:
When will the population reach 100,000?
To find when the population reaches 100,000, we first need to remember that ![]() is measured in thousands. In other words, 100,000 bacteria corresponds to
is measured in thousands. In other words, 100,000 bacteria corresponds to ![]() . Hence, we need to solve
. Hence, we need to solve ![]() .
.
Clearing denominators and dividing by 100 gives ![]() , which, after extracting square roots, produces
, which, after extracting square roots, produces ![]() or
or ![]() . Of these two solutions, only
. Of these two solutions, only ![]() in our domain, so this is the solution we keep.
in our domain, so this is the solution we keep.
Hence, it takes 4 days for the population of bacteria to reach 100,000.
Example 3.2.2.3
A mathematical model for the population ![]() , in thousands, of a certain species of bacteria,
, in thousands, of a certain species of bacteria, ![]() days after it is introduced to an environment is given by
days after it is introduced to an environment is given by ![]() ,
, ![]() .
.
Graph ![]() .
.
Solution:
Graph ![]() . \vskip 0.15em
. \vskip 0.15em
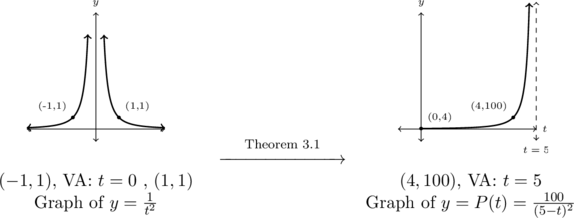
After a slight re-write, we have
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} P(t) &=& \frac{100}{(5-t)^2} \\[8pt] &=& \frac{100}{[(-1)(t-5)]^2} \\[8pt] &=& \frac{100}{(t-5)^2} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-6dfd19a235bf904c87f4d2a029248eb1_l3.png)
Using Theorem 3.1, we start with the graph of ![]() below on the left. After shifting the graph to the right
below on the left. After shifting the graph to the right ![]() units and stretching it vertically by a factor of
units and stretching it vertically by a factor of ![]() (note, the graphs are not to scale!), we restrict the domain to
(note, the graphs are not to scale!), we restrict the domain to ![]() to arrive at the graph of
to arrive at the graph of ![]() below on the right.
below on the right.
Example 3.2.2.4
A mathematical model for the population ![]() , in thousands, of a certain species of bacteria,
, in thousands, of a certain species of bacteria, ![]() days after it is introduced to an environment is given by
days after it is introduced to an environment is given by ![]() ,
, ![]() .
.
Determine and interpret the behavior of ![]() as
as ![]() .
.
Solution:
Determine and interpret the behavior of ![]() as
as ![]() .
.
We see that as ![]() ,
, ![]() .
.
This means that the population of bacteria is increasing without bound as we near 5 days, which cannot actually happen. For this reason, ![]() is called the `doomsday’ for this population. There is no way any environment can support infinitely many bacteria, so shortly before
is called the `doomsday’ for this population. There is no way any environment can support infinitely many bacteria, so shortly before ![]() days the environment would collapse.
days the environment would collapse.
Will all values excluded from the domain of a rational function produce vertical asymptotes in the graph? The short answer is `no.’ There are milder interruptions that can occur – holes in the graph – which we explore in our next example. To this end, we formalize the notion of average velocity – a concept we first encountered in Example 1.3.1.2 in Section 1.3.1. In that example, the function ![]() ,
, ![]() gives the height of a model rocket above the Moon’s surface, in feet,
gives the height of a model rocket above the Moon’s surface, in feet, ![]() seconds after liftoff. The function
seconds after liftoff. The function ![]() an example of a position function as it provides information about where the rocket is at time
an example of a position function as it provides information about where the rocket is at time ![]() . In that example, we interpreted the average rate of change of
. In that example, we interpreted the average rate of change of ![]() over an interval as the average velocity of the rocket over that interval. The average velocity provides two pieces of information: the average speed of the rocket along with the rocket’s direction. Suppose we have a position function
over an interval as the average velocity of the rocket over that interval. The average velocity provides two pieces of information: the average speed of the rocket along with the rocket’s direction. Suppose we have a position function ![]() defined over an interval containing some fixed time
defined over an interval containing some fixed time ![]() . We can define the average velocity as a function of any time
. We can define the average velocity as a function of any time ![]() other than
other than ![]() :
:
Definition 3.5
Suppose ![]() gives the position of an object at time
gives the position of an object at time ![]() and
and ![]() is a fixed time in the domain of
is a fixed time in the domain of ![]() . The average velocity between time
. The average velocity between time ![]() and time
and time ![]() is given by
is given by
![]()
provided ![]() .
.
It is clear why we must exclude ![]() from the domain of
from the domain of ![]() in Definition 3.5 because otherwise we would have a
in Definition 3.5 because otherwise we would have a ![]() in the denominator. What is interesting in this case however, is that substituting
in the denominator. What is interesting in this case however, is that substituting ![]() also produces
also produces ![]() in the numerator. (Do you see why?) While `
in the numerator. (Do you see why?) While `![]() ‘ is undefined, it is more precisely called an `indeterminate form’ and is studied extensively in Calculus. We can nevertheless explore this function in the next example.
‘ is undefined, it is more precisely called an `indeterminate form’ and is studied extensively in Calculus. We can nevertheless explore this function in the next example.
Example 3.2.3
Example 3.2.3.1
Let ![]() ,
, ![]() give the height of a model rocket above the Moon’s surface, in feet,
give the height of a model rocket above the Moon’s surface, in feet, ![]() seconds after liftoff.
seconds after liftoff.
Identify and simplify an expression for the average velocity of the rocket between times ![]() and
and ![]() .
.
Solution:
Identify and simplify an expression for the average velocity of the rocket between times ![]() and
and ![]() .
.
Using Definition 3.5 with ![]() , we get:
, we get:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \overline{v}(t) & = & \dfrac{s(t) - s(15)}{t-15} \\[10pt] & = & \dfrac{(-5t^2+100t) - 375}{t - 15} \\[10pt] & = & \dfrac{-5(t^2-20t+75)}{t - 15} \\[10pt] & = & \dfrac{-5(t-15)(t-5)}{t-15} \\[10pt] & = & \dfrac{-5\cancel{(t-15)} (t-5)}{\cancel{(t-15)}} \\[10pt] & = & -5(t-5) = -5t + 25 & \; \; t \neq 15 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-533966391aca8e90eccf4359e156f97f_l3.png)
The domain of ![]() is
is ![]() , thus our final answer is
, thus our final answer is ![]() , for
, for ![]() .
.
Example 3.2.3.2
Let ![]() ,
, ![]() give the height of a model rocket above the Moon’s surface, in feet,
give the height of a model rocket above the Moon’s surface, in feet, ![]() seconds after liftoff.
seconds after liftoff.
Compute and interpret ![]() .
.
Solution:
Compute and interpret ![]() .
.
We find ![]() .
.
This means between ![]() and
and ![]() seconds after launch, the rocket was traveling, on average a speed
seconds after launch, the rocket was traveling, on average a speed ![]() feet per second downwards, or falling back to the Moon’s surface.
feet per second downwards, or falling back to the Moon’s surface.
Example 3.2.3.3
Let ![]() ,
, ![]() give the height of a model rocket above the Moon’s surface, in feet,
give the height of a model rocket above the Moon’s surface, in feet, ![]() seconds after liftoff.
seconds after liftoff.
Graph ![]() . Interpret the intercepts.
. Interpret the intercepts.
Solution:
Graph ![]() . Interpret the intercepts.
. Interpret the intercepts.
The graph of ![]() is a portion of the line
is a portion of the line ![]() . The domain of
. The domain of ![]() is
is ![]() and
and ![]() is not defined when
is not defined when ![]() , therefore our graph is the line segment starting at
, therefore our graph is the line segment starting at ![]() and ending at
and ending at ![]() with a hole at
with a hole at ![]() .
.
The ![]() -intercept is
-intercept is ![]() which means on average, the rocket is traveling
which means on average, the rocket is traveling ![]() feet per second upwards.[6]
feet per second upwards.[6]
To get the ![]() -intercept, we set
-intercept, we set ![]() and obtain
and obtain ![]() .
.
Hence, ![]() or the average velocity between times
or the average velocity between times ![]() and
and ![]() is
is ![]() . As you may recall, this is due to the rocket being at the same altitude (
. As you may recall, this is due to the rocket being at the same altitude (![]() feet) at both times, hence,
feet) at both times, hence, ![]() and, hence
and, hence ![]() .
.

Example 3.2.3.4
Let ![]() ,
, ![]() give the height of a model rocket above the Moon’s surface, in feet,
give the height of a model rocket above the Moon’s surface, in feet, ![]() seconds after liftoff.
seconds after liftoff.
Interpret the behavior of ![]() as
as ![]() .
.
Solution:
Interpret the behavior of ![]() as
as ![]() . \vskip 0.15em
. \vskip 0.15em
From the graph, we see as ![]() ,
, ![]() . (This is also borne out in the numerically in the included tables.)
. (This is also borne out in the numerically in the included tables.)
This means as we sample the average velocity between time ![]() and and times closer and closer to
and and times closer and closer to ![]() , the average velocity approaches
, the average velocity approaches ![]() . This value is how we define the instantaneous velocity – that is, at
. This value is how we define the instantaneous velocity – that is, at ![]() seconds, the rocket is falling at a rate of
seconds, the rocket is falling at a rate of ![]() feet per second towards the surface of the Moon.
feet per second towards the surface of the Moon.
![Rendered by QuickLaTeX.com \[\begin{array}{|r||c|} \hline t & \overline{v}(t) \\ \hline 14.9 & -49.5 \\ \hline 14.99 & -49.95 \\ \hline 14.999 & -49.995 \\ \hline 15 & \text{undefined} \\ \hline 15.001 & -50.005 \\ \hline 15.01 & -50.05 \\ \hline 15.1 & -50.5 \\ \hline \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e16d0bc99bd031861194e32a46232406_l3.png)
If nothing else, Example 3.2.3 shows us that just because a value is excluded from the domain of a rational function doesn’t mean there will be a vertical asymptote to the graph there. In this case, the factor ![]() divided out from the denominator, thereby effectively removing the threat of dividing by
divided out from the denominator, thereby effectively removing the threat of dividing by ![]() . It turns out, this situation generalizes to the theorem below.
. It turns out, this situation generalizes to the theorem below.
Theorem 3.2 Location of Vertical Asymptotes and Holes[7]
Suppose ![]() is a rational function which can be written as
is a rational function which can be written as ![]() where
where ![]() and
and ![]() have no common zeros.[8] Let
have no common zeros.[8] Let ![]() be a real number which is not in the domain of
be a real number which is not in the domain of ![]() .
.
- If
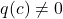 , then the graph of
, then the graph of 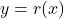 has a hole at
has a hole at 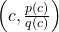
- If
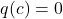 , then the line
, then the line  is a vertical asymptote of the graph of
is a vertical asymptote of the graph of 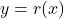 .
.
In English, Theorem 3.2 says that if ![]() is not in the domain of
is not in the domain of ![]() but, when we simplify
but, when we simplify ![]() , it no longer makes the denominator
, it no longer makes the denominator ![]() , then we have a hole at
, then we have a hole at ![]() . Otherwise, the line
. Otherwise, the line ![]() is a vertical asymptote of the graph of
is a vertical asymptote of the graph of ![]() . Like many properties of rational functions, we owe Theorem 3.2 to Calculus, but that won’t stop us from putting Theorem 3.2 to good use in the following example.
. Like many properties of rational functions, we owe Theorem 3.2 to Calculus, but that won’t stop us from putting Theorem 3.2 to good use in the following example.
Example 3.2.4
Example 3.2.4.1
For each function below:
![]()
- determine the values excluded from the domain.
- determine whether each excluded value corresponds to a vertical asymptote or hole of the graph.
- verify your answers with a rough sketch of a graph.
- describe the behavior of the graph near each excluded value using proper notation.
- investigate any apparent symmetry of the graph about the
 -axis or origin.
-axis or origin.
Solution:
Determine the vertical behavior of ![]() .
.
To use Theorem 3.2, we first find all of the real numbers which aren’t in the domain of ![]() . To do so, we solve
. To do so, we solve ![]() and get
and get ![]() .
.
Because the expression ![]() is in lowest terms (can you see why?), there is no division of like factors possible, and we conclude that the lines
is in lowest terms (can you see why?), there is no division of like factors possible, and we conclude that the lines ![]() and
and ![]() are vertical asymptotes to the graph of
are vertical asymptotes to the graph of ![]() . The graph verifies this claim, and from the graph, we see that as
. The graph verifies this claim, and from the graph, we see that as ![]() ,
, ![]() , as
, as ![]() ,
, ![]() , as
, as ![]() ,
, ![]() , and finally as
, and finally as ![]() ,
, ![]() .
.
As a side note, the graph of ![]() appears to be symmetric about the origin. Sure enough, we find:
appears to be symmetric about the origin. Sure enough, we find: ![]() , proving
, proving ![]() is odd.
is odd.
Example 3.2.4.2
For each function below:
![]()
- determine the values excluded from the domain.
- determine whether each excluded value corresponds to a vertical asymptote or hole of the graph.
- verify your answers with a rough sketch of a graph.
- describe the behavior of the graph near each excluded value using proper notation.
- investigate any apparent symmetry of the graph about the
 -axis or origin.
-axis or origin.
Solution:
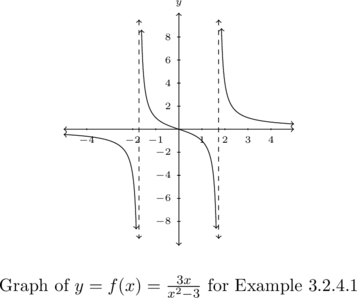
Determine the vertical behavior of ![]() .
.
As above, we find the values excluded from the domain of ![]() by setting the denominator equal to
by setting the denominator equal to ![]() . Solving
. Solving ![]() gives
gives ![]() .
.
In lowest terms
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(t) &=& \frac{t^2-t-6}{t^2-9} \\ &=& \frac{(t-3)(t+2)}{(t-3)(t+3)} \\ &=& \frac{t+2}{t+3} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d69b68b4ed4af41cc3109ae196998741_l3.png)
Because ![]() continues to be a zero of the denominator in the reduced formula, we know the line
continues to be a zero of the denominator in the reduced formula, we know the line ![]() is a vertical asymptote to the graph of
is a vertical asymptote to the graph of ![]() .
.
AS ![]() does not produce a `
does not produce a `![]() ‘ in the denominator of the reduced formula, we have a hole at
‘ in the denominator of the reduced formula, we have a hole at ![]() .
.
To find the ![]() -coordinate of the hole, we substitute
-coordinate of the hole, we substitute ![]() into the reduced formula:
into the reduced formula: ![]() so the hole is at
so the hole is at ![]() .
.
Graphing ![]() we can definitely see the vertical asymptote
we can definitely see the vertical asymptote ![]() : as
: as ![]() ,
, ![]() and as
and as ![]() ,
, ![]() . Near
. Near ![]() , the graph seems to have no interruptions (but we know
, the graph seems to have no interruptions (but we know ![]() is undefined at
is undefined at ![]() .) As
.) As ![]() appears to be increasing on
appears to be increasing on ![]() , we write as
, we write as ![]() ,
, ![]() , and as
, and as ![]() ,
, ![]() .
.

Example 3.2.4.3
For each function below:
![]()
- determine the values excluded from the domain.
- determine whether each excluded value corresponds to a vertical asymptote or hole of the graph.
- verify your answers with a rough sketch of a graph.
- describe the behavior of the graph near each excluded value using proper notation.
- investigate any apparent symmetry of the graph about the
 -axis or origin.
-axis or origin.
Solution:
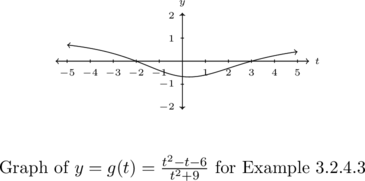
Determine the vertical behavior of ![]() .
.
Setting the denominator of the expression for ![]() to
to ![]() gives
gives ![]() , which has no real solutions. Accordingly, the graph of
, which has no real solutions. Accordingly, the graph of ![]() (at least as much as we can discern from the technology) is devoid of both vertical asymptotes and holes.
(at least as much as we can discern from the technology) is devoid of both vertical asymptotes and holes.
Example 3.2.4.4
For each function below:
![]()
- determine the values excluded from the domain.
- determine whether each excluded value corresponds to a vertical asymptote or hole of the graph.
- verify your answers with a rough sketch of a graph.
- describe the behavior of the graph near each excluded value using proper notation.
- investigate any apparent symmetry of the graph about the
 -axis or origin.
-axis or origin.
Solution:
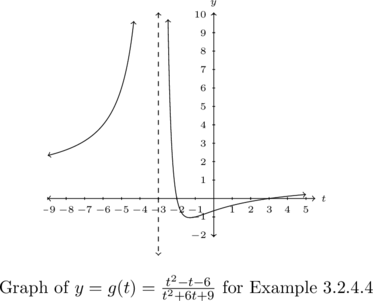
Determine the vertical behavior of ![]() .
.
Setting the denominator of ![]() to zero gives the equation
to zero gives the equation ![]() . We get the (repeated!) solution
. We get the (repeated!) solution ![]() .
.
Simplifying, we see
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} r(t) &=& \frac{t^2-t-6}{t^2+6t+9}\\ &=& \frac{(t-3)(t+3)}{(t+3)^2}\\ &=& \frac{t-3}{t+3} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c547e94f11772b66d2bf0ef54ea7386a_l3.png)
Because ![]() continues to produce a
continues to produce a ![]() in the denominator of the reduced function, we know
in the denominator of the reduced function, we know ![]() is a vertical asymptote to the graph. The calculator bears this out, and, moreover, we see that as
is a vertical asymptote to the graph. The calculator bears this out, and, moreover, we see that as ![]() ,
, ![]() and as
and as ![]() ,
, ![]() .
.
3.2.3 End Behavior
Now that we’ve thoroughly discussed behavior near values excluded from the domains of rational functions, focus our attention on end behavior. We have already seen one example of this in the form of horizontal asymptotes. Our next example of the section gives us a real-world application of a horizontal asymptote.[9]
Example 3.2.4
Example 3.2.5.1
The number of students ![]() at local college who have had the flu
at local college who have had the flu ![]() months after the semester begins can be modeled by:
months after the semester begins can be modeled by:
![]()
Compute and interpret ![]() .
.
Solution:
Compute and interpret ![]() .
.
Substituting ![]() gives
gives ![]() .
.
As ![]() represents the number of months since the beginning of the semester,
represents the number of months since the beginning of the semester, ![]() describes the state of the flu outbreak at the beginning of the semester. Hence, at the beginning of the semester,
describes the state of the flu outbreak at the beginning of the semester. Hence, at the beginning of the semester, ![]() students have had the flu.
students have had the flu.
Example 3.2.5.2
The number of students ![]() at local college who have had the flu
at local college who have had the flu ![]() months after the semester begins can be modeled by:
months after the semester begins can be modeled by:
![]()
How long will it take until ![]() students will have had the flu?
students will have had the flu?
Solution:
How long will it take until ![]() students will have had the flu?
students will have had the flu?
We set ![]() and solve.
and solve.
Clearing denominators gives ![]() from which we get
from which we get ![]() .
.
This means it will take ![]() months, or about 13 days, for
months, or about 13 days, for ![]() students to have had the flu.
students to have had the flu.
Example 3.2.5.3
The number of students ![]() at local college who have had the flu
at local college who have had the flu ![]() months after the semester begins can be modeled by:
months after the semester begins can be modeled by:
![]()
Use Theorem 3.1 to graph ![]() .
.
Solution:
Use Theorem 3.1 to graph ![]() .
.
To graph ![]() , we first use long division to rewrite
, we first use long division to rewrite ![]() . From there, we get
. From there, we get
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} N(t) &=& -\frac{450}{3t+1} + 500 \\[6pt] &=& \frac{-450}{3\left(t + \frac{1}{3}\right)} + 500 \\[6pt] &=& \frac{-150}{t+\frac{1}{3}} + 500 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5589636c6751ad6fe7eecc2484adb0c0_l3.png)
Using Theorem 3.1, we start with the graph of ![]() below on the left and perform the following steps: shift the graph to the left by
below on the left and perform the following steps: shift the graph to the left by ![]() units, stretch the graph vertically by a factor of
units, stretch the graph vertically by a factor of ![]() , reflect the graph across the
, reflect the graph across the ![]() -axis, and finally, shift the graph up
-axis, and finally, shift the graph up ![]() units.
units.
As the domain of ![]() is
is ![]() , we obtain the graph below on the right.
, we obtain the graph below on the right.
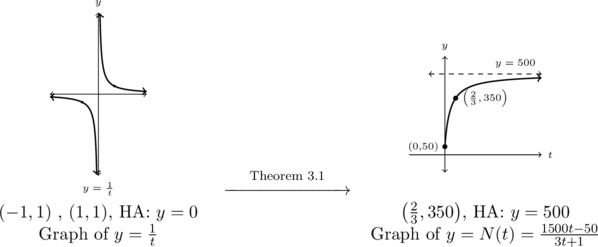
Example 3.2.5.4
The number of students ![]() at local college who have had the flu
at local college who have had the flu ![]() months after the semester begins can be modeled by:
months after the semester begins can be modeled by:
![]()
Determine and interpret the behavior of ![]() as
as ![]() .
.
Solution:
Determine and interpret the behavior of ![]() as
as ![]() .
.
From the graph, we see as ![]() ,
, ![]() . (More specifically,
. (More specifically, ![]() .) This means as time goes by, only a total of 500 students will have ever had the flu.
.) This means as time goes by, only a total of 500 students will have ever had the flu.
We determined the horizontal asymptote to the graph of ![]() by rewriting
by rewriting ![]() into a form compatible with Theorem 3.1, and while there is nothing wrong with this approach, it will simply not work for general rational functions which cannot be rewritten this way. To that end, we revisit this problem using Theorem 2.4 from Section 2.2.
into a form compatible with Theorem 3.1, and while there is nothing wrong with this approach, it will simply not work for general rational functions which cannot be rewritten this way. To that end, we revisit this problem using Theorem 2.4 from Section 2.2.
The end behavior of the numerator of ![]() is determined by its leading term,
is determined by its leading term, ![]() , and the end behavior of the denominator is likewise determined by its leading term,
, and the end behavior of the denominator is likewise determined by its leading term, ![]() . Hence, as
. Hence, as ![]() ,
,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} N(t) &=& \dfrac{1500t + 50}{3t+1} \\[6pt] &\approx & \dfrac{1500t}{3t} \\[6pt] &=& 500 \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-137d21f140e7a2f0d38a7405f01c4569_l3.png)
Hence as ![]() ,
, ![]() , producing the horizontal asymptote
, producing the horizontal asymptote ![]() .
.
This same reasoning can be used in general to argue the following theorem.
Theorem 3.3 Location of Horizontal Asymptotes
Suppose ![]() is a rational function and
is a rational function and ![]() , where
, where ![]() and
and ![]() are polynomial functions with leading coefficients
are polynomial functions with leading coefficients ![]() and
and ![]() , respectively.
, respectively.
- If the degree of
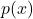 is the same as the degree of
is the same as the degree of 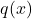 , then
, then 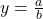 is the[10] horizontal asymptote of the graph of
is the[10] horizontal asymptote of the graph of 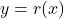 .
. - If the degree of
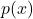 is less than the degree of
is less than the degree of 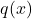 , then
, then  is the horizontal asymptote of the graph of
is the horizontal asymptote of the graph of 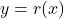 .
. - If the degree of
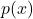 is greater than the degree of
is greater than the degree of 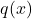 , then the graph of
, then the graph of 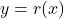 has no horizontal asymptotes.
has no horizontal asymptotes.
So see why Theorem 3.3 works, suppose ![]() where
where ![]() is the leading coefficient of
is the leading coefficient of ![]() and
and ![]() is the leading coefficient of
is the leading coefficient of ![]() . As
. As ![]() , Theorem 2.4 gives
, Theorem 2.4 gives ![]() , where
, where ![]() and
and ![]() are the degrees of
are the degrees of ![]() and
and ![]() , respectively.
, respectively.
If the degree of ![]() and the degree of
and the degree of ![]() are the same, then
are the same, then ![]() so that
so that ![]() , which means
, which means ![]() is the horizontal asymptote in this case.
is the horizontal asymptote in this case.
If the degree of ![]() is less than the degree of
is less than the degree of ![]() , then
, then ![]() , so
, so ![]() is a positive number, and hence,
is a positive number, and hence, ![]() . As
. As ![]() ,
, ![]() is more or less a fraction with a constant numerator,
is more or less a fraction with a constant numerator, ![]() , but a denominator which is unbounded. Hence,
, but a denominator which is unbounded. Hence, ![]() producing the horizontal asymptote
producing the horizontal asymptote ![]() .
.
If the degree of ![]() is greater than the degree of
is greater than the degree of ![]() , then
, then ![]() , and hence
, and hence ![]() is a positive number and
is a positive number and ![]() , which is a monomial function from Section 2.2. As such,
, which is a monomial function from Section 2.2. As such, ![]() becomes unbounded as
becomes unbounded as ![]() .
.
Note that in the two cases which produce horizontal asymptotes, the behavior of ![]() is identical as
is identical as ![]() and
and ![]() . Hence, if the graph of a rational function has a horizontal asymptote, there is only one.[11]
. Hence, if the graph of a rational function has a horizontal asymptote, there is only one.[11]
We put Theorem 3.3 to good use in the following example.
Example 3.2.6
Example 3.2.6.1
For each function below:
![]()
- use Theorem 2.4 to analytically determine the horizontal asymptotes of the graph, if any.
- check your answers using Theorem 3.3 and a graph.
- describe the end behavior of the graph using proper notation.
- investigate any apparent symmetry of the graph about the
 -axis or origin.
-axis or origin.
Solution:
Determine the horizontal behavior of ![]() .
.
Using Theorem 2.4, we get as ![]() ,
,
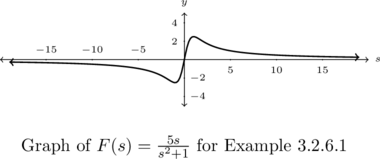
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} F(s) &=& \frac{5s}{s^2+1}\\ [6pt] &\approx& \frac{5s}{s^2} \\[6pt] &=& \frac{5}{s} \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f30b549cd05775a266d77a437b97bf8a_l3.png)
Hence, as ![]() ,
, ![]() , so
, so ![]() is a horizontal asymptote to the graph of
is a horizontal asymptote to the graph of ![]() .
.
To check, we note that the degree of the numerator of ![]() ,
, ![]() , is less than the degree of the denominator,
, is less than the degree of the denominator, ![]() , so Theorem 3.3 gives
, so Theorem 3.3 gives ![]() is the horizontal asymptote. Graphically, we see as
is the horizontal asymptote. Graphically, we see as ![]() ,
, ![]() . More specifically, as
. More specifically, as ![]() ,
, ![]() and as
and as ![]() ,
, ![]() .
.
As a side note, the graph of ![]() appears to be symmetric about the origin. Indeed,
appears to be symmetric about the origin. Indeed, ![]() proving
proving ![]() is odd.
is odd.
Example 3.2.6.2
For each function below:
![]()
- use Theorem 2.4 to analytically determine the horizontal asymptotes of the graph, if any.
- check your answers using Theorem 3.3 and a graph.
- describe the end behavior of the graph using proper notation.
- investigate any apparent symmetry of the graph about the
 -axis or origin.
-axis or origin.
Solution:
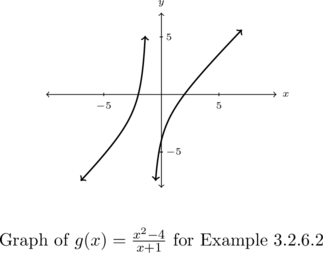
Determine the horizontal behavior of ![]() . \vskip 0.15em
. \vskip 0.15em
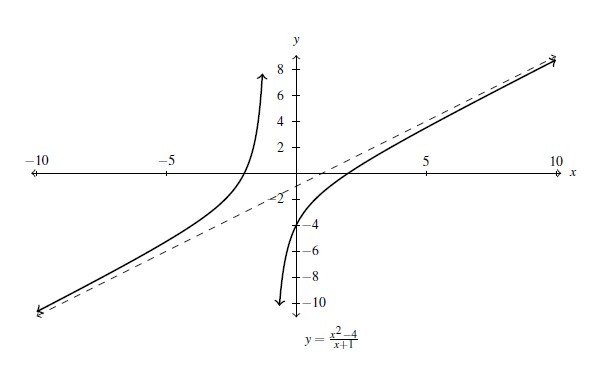
As ![]() ,
,
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(x) &=& \frac{x^2-4}{x+1} \\[6pt] &\approx & \frac{x^2}{x} \\[6pt] &=& x \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-23f8286af80ed6c510adaea303e10324_l3.png)
and while ![]() is a line, it is not a horizontal line. Hence, we conclude the graph of
is a line, it is not a horizontal line. Hence, we conclude the graph of ![]() has no horizontal asymptotes.
has no horizontal asymptotes.
Sure enough, Theorem 3.3 supports this as the degree of the numerator of ![]() is
is ![]() which is greater than the degree of the denominator,
which is greater than the degree of the denominator, ![]() . By, there is no horizontal asymptote. From the graph, we see that the graph of
. By, there is no horizontal asymptote. From the graph, we see that the graph of ![]() doesn’t appear to level off to a constant value, so there is no horizontal asymptote.[12]
doesn’t appear to level off to a constant value, so there is no horizontal asymptote.[12]
Example 3.2.6.3
For each function below:
![]()
- use Theorem 2.4 to analytically determine the horizontal asymptotes of the graph, if any.
- check your answers using Theorem 3.3 and a graph.
- describe the end behavior of the graph using proper notation.
- investigate any apparent symmetry of the graph about the
 -axis or origin.
-axis or origin.
Solution:
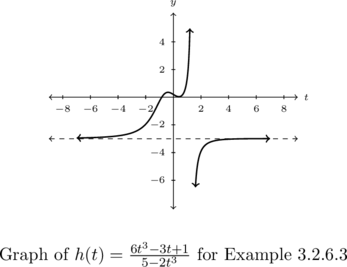
Determine the horizontal behavior of ![]() .
.
We have
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} h(t) &=& \frac{6t^3-3t+1}{5-2t^3}\\[6pt] &\approx & \frac{6t^3}{-2t^3} \\[6pt] &=& -3\end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5771c9cf50c9607a16c2aabef61bd9b6_l3.png)
as ![]() , indicating a horizontal asymptote
, indicating a horizontal asymptote ![]() .
.
Sure enough, the degrees of the numerator and denominator of ![]() are both three, so Theorem 3.3 tells us
are both three, so Theorem 3.3 tells us ![]() is the horizontal asymptote. We see from the graph of
is the horizontal asymptote. We see from the graph of ![]() that as
that as ![]() ,
, ![]() , and as
, and as ![]() ,
, ![]() .
.
Example 3.2.6.4
For each function below:
![]()
- use Theorem 2.4 to analytically determine the horizontal asymptotes of the graph, if any.
- check your answers using Theorem 3.3 and a graph.
- describe the end behavior of the graph using proper notation.
- investigate any apparent symmetry of the graph about the
 -axis or origin.
-axis or origin.
Solution:
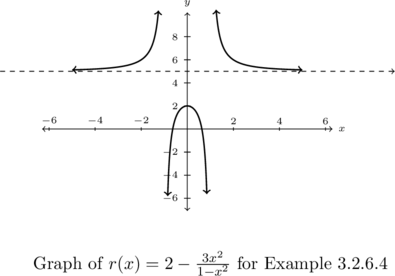
Determine the horizontal behavior of ![]() .
.
If we apply Theorem 2.4 to the ![]() term in the expression for
term in the expression for ![]() , we find
, we find
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \frac{3x^2}{1-x^2} &\approx & \frac{3x^2}{-x^2} \\[6pt] &=& -3 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-24909a05b98f410f813cb0879e7fe411_l3.png)
as ![]() . It seems reasonable to conclude, then, that
. It seems reasonable to conclude, then, that
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} r(x) &=& 2 - \frac{3x^2}{1-x^2} \\[6pt] &\approx & 2 - (-3) \\[6pt] &=& 5 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7112c122c461a6d28360312b56169ef2_l3.png)
so ![]() is our horizontal asymptote.
is our horizontal asymptote.
In order to use Theorem 3.3 as stated, however, we need to rewrite the expression ![]() with a single denominator:
with a single denominator: ![]() . Now we apply Theorem 3.3 and note the numerator and denominator have the same degree, we guarantee the horizontal asymptote is
. Now we apply Theorem 3.3 and note the numerator and denominator have the same degree, we guarantee the horizontal asymptote is ![]() . These calculations are borne out graphically where it appears as if as
. These calculations are borne out graphically where it appears as if as ![]() ,
, ![]() .
.
As a final note, the graph of ![]() appears to be symmetric about the
appears to be symmetric about the ![]() -axis. We find
-axis. We find ![]() , proving
, proving ![]() is even.
is even.
We close this section with a discussion of the third (and final!) kind of asymptote which can be associated with the graphs of rational functions. Let us return to the function ![]() in Example 3.2.6.2. Performing long division,[13] we get
in Example 3.2.6.2. Performing long division,[13] we get ![]() . Because the term
. Because the term ![]() as
as ![]() , it stands to reason that as
, it stands to reason that as ![]() becomes unbounded, the function values
becomes unbounded, the function values ![]() . Geometrically, this means that the graph of
. Geometrically, this means that the graph of ![]() should resemble the line
should resemble the line ![]() as
as ![]() . We see this play out both numerically and graphically below. (As usual, the asymptote
. We see this play out both numerically and graphically below. (As usual, the asymptote ![]() is denoted by a dashed line.)
is denoted by a dashed line.)
![Rendered by QuickLaTeX.com \[ \begin{array}{ccc} \begin{array}{|r||c|c|} \hline x & g(x) & x-1 \\ \hline -10 & \approx -10.6667 & -11 \\ \hline -100 & \approx -100.9697 & -101 \\ \hline -1000 & \approx -1000.9970& -1001 \\ \hline -10000 & \approx -10000.9997 & -10001 \\ \hline \end{array} & \qquad \qquad & \begin{array}{|r||c|c|} \hline x & g(x) & x-1 \\ \hline 10 & \approx 8.7273 & 9 \\\hline 100 & \approx 98.9703 & 99 \\ \hline 1000 & \approx 998.9970 & 999 \\ \hline 10000 & \approx 9998.9997 & 9999 \\ \hline \end{array}\\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-11b797929449783765ea077ee1c40fd7_l3.png)
The way we symbolize the relationship between the end behavior of ![]() with that of the line
with that of the line ![]() is to write `as
is to write `as ![]() ,
, ![]() ‘ in order to have some notational consistency with what we have done earlier in this section when it comes to end behavior.[14] In this case, we say the line
‘ in order to have some notational consistency with what we have done earlier in this section when it comes to end behavior.[14] In this case, we say the line ![]() is a slant asymptote[15] of the graph of
is a slant asymptote[15] of the graph of ![]() . Informally, the graph of a rational function has a slant asymptote if, as
. Informally, the graph of a rational function has a slant asymptote if, as ![]() or as
or as ![]() , the graph resembles a non-horizontal, or `slanted’ line. Formally, we define a slant asymptote as follows.
, the graph resembles a non-horizontal, or `slanted’ line. Formally, we define a slant asymptote as follows.
Definition 3.6
The line ![]() where
where ![]() is called a slant asymptote of the graph of a function
is called a slant asymptote of the graph of a function ![]() if as
if as ![]() or as
or as ![]() ,
, ![]() .
.
A few remarks are in order. First, note that the stipulation ![]() in Definition 3.6 is what makes the `slant’ asymptote `slanted’ as opposed to the case when
in Definition 3.6 is what makes the `slant’ asymptote `slanted’ as opposed to the case when ![]() in which case we’d have a horizontal asymptote. Secondly, while we have motivated what me mean intuitively by the notation `
in which case we’d have a horizontal asymptote. Secondly, while we have motivated what me mean intuitively by the notation `![]() ,’ like so many ideas in this section, the formal definition requires Calculus. Another way to express this sentiment, however, is to rephrase `
,’ like so many ideas in this section, the formal definition requires Calculus. Another way to express this sentiment, however, is to rephrase `![]() ‘ as `
‘ as `![]() .’ In other words, the graph of
.’ In other words, the graph of ![]() has the slant asymptote
has the slant asymptote ![]() if and only if the graph of
if and only if the graph of ![]() has a horizontal asymptote
has a horizontal asymptote ![]() . If we wanted to, we could introduce the notations
. If we wanted to, we could introduce the notations ![]() to mean
to mean ![]() and
and ![]() to mean
to mean ![]() , but these non-standard notations.
, but these non-standard notations.
Theorem 3.4 Determination of Slant Asymptotes
Suppose ![]() is a rational function and
is a rational function and ![]() , where the degree of
, where the degree of ![]() is exactly one more than the degree of
is exactly one more than the degree of ![]() . Then the graph of
. Then the graph of ![]() has the slant asymptote
has the slant asymptote ![]() where
where ![]() is the quotient obtained by dividing
is the quotient obtained by dividing ![]() by
by ![]() .
.
In the same way that Theorem 3.3 gives us an easy way to see if the graph of a rational function ![]() has a horizontal asymptote by comparing the degrees of the numerator and denominator, Theorem 3.4 gives us an easy way to check for slant asymptotes. Unlike Theorem 3.3, which gives us a quick way to find the horizontal asymptotes (if any exist), Theorem 3.4 gives us no such `short-cut’. If a slant asymptote exists, we have no recourse but to use long division to find it.[16]
has a horizontal asymptote by comparing the degrees of the numerator and denominator, Theorem 3.4 gives us an easy way to check for slant asymptotes. Unlike Theorem 3.3, which gives us a quick way to find the horizontal asymptotes (if any exist), Theorem 3.4 gives us no such `short-cut’. If a slant asymptote exists, we have no recourse but to use long division to find it.[16]
Example 3.2.7
Example 3.2.7.1
For each function below:
![]()
- identify the slant asymptote, if it exists.
- verify your answer using a graph.
- investigate any apparent symmetry of the graph about the
 -axis or origin.
-axis or origin.
Solution:
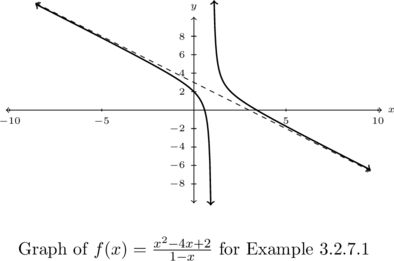
Determine any slant asymptotes of ![]() .
.
The degree of the numerator is ![]() and the degree of the denominator is
and the degree of the denominator is ![]() , so Theorem 3.4 guarantees a slant asymptote exists. To find it, we divide
, so Theorem 3.4 guarantees a slant asymptote exists. To find it, we divide ![]() into
into ![]() and get a quotient of
and get a quotient of ![]() , so our slant asymptote is
, so our slant asymptote is ![]() .
.
We confirm this graphically below.
Example 3.2.7.2
For each function below:
![]()
- identify the slant asymptote, if it exists.
- verify your answer using a graph.
- investigate any apparent symmetry of the graph about the
 -axis or origin.
-axis or origin.
Solution:
Determine any slant asymptotes of ![]() .
.
As with the previous example, the degree of the numerator ![]() is
is ![]() and the degree of the denominator is
and the degree of the denominator is ![]() , so Theorem 3.4 applies. In this case,
, so Theorem 3.4 applies. In this case,
![Rendered by QuickLaTeX.com \[\begin{array}{rcl} g(t) &=& \frac{t^2-4}{t-2} \\[6pt] &=& \frac{(t+2)(t-2)}{(t-2)} \\[6pt] &=& \frac{(t+2) \cancel{(t-2)}}{\cancelto{1}{(t-2)}} \\[6pt] &=& t+2, \quad t \neq 2 \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-72dfb27f33b83bde452e110bd563c480_l3.png)
so we have that the slant asymptote, ![]() , is identical to the graph of
, is identical to the graph of ![]() except at
except at ![]() (where the latter has a `hole’ at
(where the latter has a `hole’ at ![]() .) While the word `asymptote’ has the connotation of `approaching but not equaling,’ Definitions 3.6 and 3.4 allow for these extreme cases.
.) While the word `asymptote’ has the connotation of `approaching but not equaling,’ Definitions 3.6 and 3.4 allow for these extreme cases.

Example 3.2.7.3
For each function below:
![]()
- identify the slant asymptote, if it exists.
- verify your answer using a graph.
- investigate any apparent symmetry of the graph about the
 -axis or origin.
-axis or origin.
Solution:
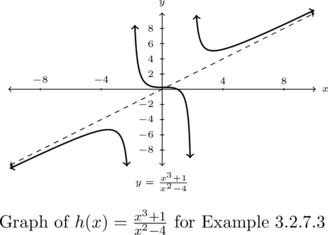
Determine any slant asymptotes of ![]() .
.
For ![]() , the degree of the numerator is
, the degree of the numerator is ![]() and the degree of the denominator is
and the degree of the denominator is ![]() , so again, we are guaranteed the existence of a slant asymptote. The long division
, so again, we are guaranteed the existence of a slant asymptote. The long division ![]() gives a quotient of just
gives a quotient of just ![]() , so our slant asymptote is the line
, so our slant asymptote is the line ![]() .
.
The graph confirms this.
Note the graph of ![]() appears to be symmetric about the origin. We check
appears to be symmetric about the origin. We check ![]() . However,
. However, ![]() , so it appears as if
, so it appears as if ![]() for all
for all ![]() . Checking
. Checking ![]() , we find
, we find ![]() but
but ![]() which shows the graph of
which shows the graph of ![]() , is in fact, not symmetric about the origin.
, is in fact, not symmetric about the origin.
Example 3.2.7.4
For each function below:
![]()
- identify the slant asymptote, if it exists.
- verify your answer using a graph.
- investigate any apparent symmetry of the graph about the
 -axis or origin.
-axis or origin.
Solution:
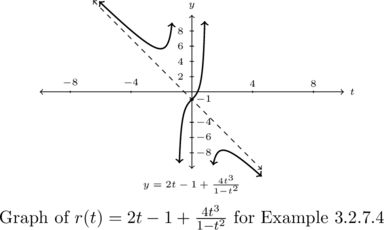
Determine any slant asymptotes of ![]() . \vskip 0.15em
. \vskip 0.15em
For our last example, ![]() , the expression
, the expression ![]() is not in the form to apply Theorem 3.4 directly. We can, nevertheless, appeal to the spirit of the theorem and use long division to rewrite the term
is not in the form to apply Theorem 3.4 directly. We can, nevertheless, appeal to the spirit of the theorem and use long division to rewrite the term ![]() . We then get:
. We then get:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} r(t) & = & 2t-1+\dfrac{4t^3}{1-t^2} \\ &= & 2t-1-4t+\dfrac{4t}{1-t^2} \\ & = & -2t-1 + \dfrac{4t}{1-t^2} \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-233ebe972db057d0e49152446fe6b1fd_l3.png)
As ![]() , Theorem 2.4 gives
, Theorem 2.4 gives ![]() . Hence, as
. Hence, as ![]() ,
, ![]() , so
, so ![]() is the slant asymptote to the graph as confirmed by the graph below.
is the slant asymptote to the graph as confirmed by the graph below.
From a distance, the graph of ![]() appears to be symmetric about the origin. However, if we look carefully, we see the
appears to be symmetric about the origin. However, if we look carefully, we see the ![]() -intercept is
-intercept is ![]() , as borne out by the computation
, as borne out by the computation ![]() . Hence
. Hence ![]() cannot be odd. (Do you see why?)
cannot be odd. (Do you see why?)
Our last example gives a real-world application of a slant asymptote. The problem features the concept of average profit. The average profit, denoted ![]() , is the total profit,
, is the total profit, ![]() , divided by the number of items sold,
, divided by the number of items sold, ![]() . In English, the average profit tells us the profit made per item sold. It, along with average cost, is defined below.
. In English, the average profit tells us the profit made per item sold. It, along with average cost, is defined below.
Definition 3.7
Let ![]() and
and ![]() represent the cost and profit to make and sell
represent the cost and profit to make and sell ![]() items, respectively.
items, respectively.
- The average cost,
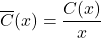 ,
, 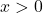 .
.
NOTE: The average cost is the cost per item produced. - The average profit,
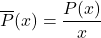 ,
, 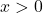 .
.
NOTE:} The average profit is the profit per item sold.
You’ll explore average cost (and its relation to variable cost) in Exercise 37. For now, we refer the reader to to Example 2.1.3 in Section 2.1.
Example 3.2.8
Example 3.2.8.1
Recall the profit (in dollars) when ![]() PortaBoy game systems are produced and sold is given by
PortaBoy game systems are produced and sold is given by ![]() ,
, ![]() .
.
Determine and simplify an expression for the average profit, ![]() . What is the domain of
. What is the domain of ![]() ?
?
Solution:
Determine and simplify an expression for the average profit, ![]() . What is the domain of
. What is the domain of ![]() ?
?
We find
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \overline{P}(x) &=& \frac{P(x)}{x} \\[6pt] &=& \frac{ -1.5x^2+170x-150}{x}\\[6pt] &=& -1.5x + 170 - \frac{150}{x} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7861d64ba8b00b6d139185321b3eaf82_l3.png)
While the domain of ![]() is
is ![]() ,
, ![]() , thus the domain of
, thus the domain of ![]() is
is ![]() .
.
Example 3.2.8.2
Recall the profit (in dollars) when ![]() PortaBoy game systems are produced and sold is given by
PortaBoy game systems are produced and sold is given by ![]() ,
, ![]() .
.
Compute and interpret ![]() .
.
Solution:
Compute and interpret ![]() .
.
We find ![]() .
.
This means that when 50 PortaBoy systems are sold, the average profit is 92 dollars per system.
Example 3.2.8.3
Recall the profit (in dollars) when ![]() PortaBoy game systems are produced and sold is given by
PortaBoy game systems are produced and sold is given by ![]() ,
, ![]() .
.
Determine the slant asymptote to the graph of ![]() . Check your answer using a graph.
. Check your answer using a graph.
Solution:
Determine the slant asymptote to the graph of ![]() . Check your answer using a graph.
. Check your answer using a graph.
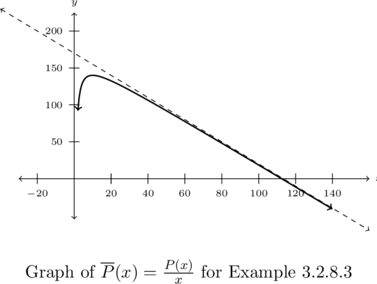
Technically, the graph of ![]() has no slant asymptote because the domain of the function is restricted to
has no slant asymptote because the domain of the function is restricted to ![]() .
.
That being said, if we were to let ![]() , the term
, the term ![]() , so we’d have
, so we’d have ![]() . This means the slant asymptote would be
. This means the slant asymptote would be ![]() .
.
We graph ![]() and
and ![]() .
.
Example 3.2.8.4
Recall the profit (in dollars) when ![]() PortaBoy game systems are produced and sold is given by
PortaBoy game systems are produced and sold is given by ![]() ,
, ![]() .
.
Interpret the slope of the slant asymptote.
Solution:
Interpret the slope of the slant asymptote.
The slope of the slant asymptote ![]() is
is ![]() . Because, ostensibly
. Because, ostensibly ![]() , this means that, as we sell more systems, the average profit is decreasing at about a rate of 1.50 dollars per system.
, this means that, as we sell more systems, the average profit is decreasing at about a rate of 1.50 dollars per system.
If the number 1.5 sounds familiar to this problem situation, it should. In Example 1.3.9 in Section 1.3.1, we determined the slope of the demand function to be ![]() . In that situation, the
. In that situation, the ![]() meant that in order to sell an additional system, the price had to drop by 1.50 dollars. The fact the average profit is decreasing at more or less this same rate means the loss in profit per system can be attributed to the reduction in price needed to sell each additional system.[17]
meant that in order to sell an additional system, the price had to drop by 1.50 dollars. The fact the average profit is decreasing at more or less this same rate means the loss in profit per system can be attributed to the reduction in price needed to sell each additional system.[17]
3.2.4 Section Exercises
(Review of Long Division):[18] In Exercises 1 – 6, use polynomial long division to perform the indicated division. Write the polynomial in the form ![]() .
.
In Exercises 7 – 10, given the pair of functions ![]() and
and ![]() , sketch the graph of
, sketch the graph of ![]() by starting with the graph of
by starting with the graph of ![]() and using Theorem 3.1. Track at least two points and the asymptotes. State the domain and range using interval notation.
and using Theorem 3.1. Track at least two points and the asymptotes. State the domain and range using interval notation.
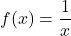 and
and 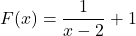
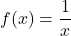 and
and 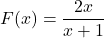
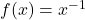 and
and 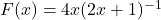
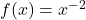 and
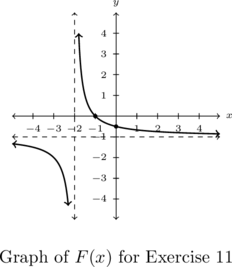
and 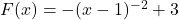
In Exercises 11 – 12, find a formula for each function below in the form ![]() .
.
-
 -intercept
-intercept 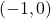 ,
,  -intercept
-intercept 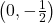
-
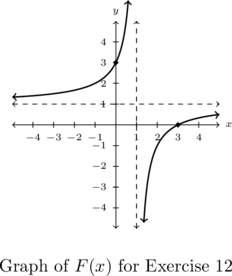
 -intercept
-intercept  ,
,  -intercept
-intercept 
In Exercises 13 – 14, find a formula for each function below in the form ![]() .
.
-
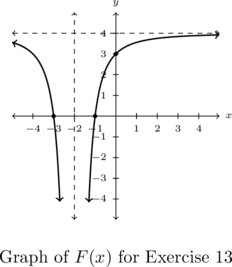
 -intercepts
-intercepts 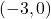 ,
, 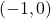 ,
,  -intercept
-intercept 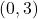
-
 -intercepts
-intercepts 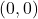 ,
, 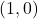 , vertical asymptote:
, vertical asymptote: 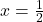
In Exercises 15 – 32, for the given rational function:
- State the domain.
- Identify any vertical asymptotes of the graph.
- Identify any holes in the graph.
- Determine the horizontal asymptote, if it exists.
- Determine the slant asymptote, if it exists.
- Graph the function and describe the behavior near the asymptotes.
-
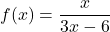
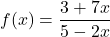
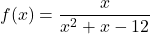
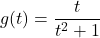
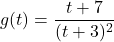
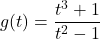
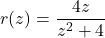
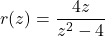
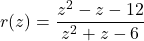
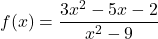
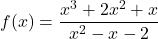
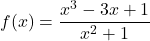
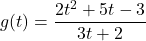
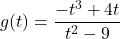
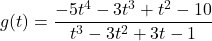
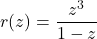
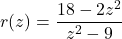
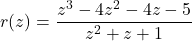
- The cost
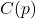 in dollars to remove
in dollars to remove 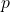 \% of the invasive Ippizuti fish species from Sasquatch Pond is:
\% of the invasive Ippizuti fish species from Sasquatch Pond is:
![Rendered by QuickLaTeX.com \[C(p) = \frac{1770p}{100 - p}, \quad 0 \leq p < 100 \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4ea7b99423b0bbdbbd87f7ddcef922bb_l3.png)
- Compute and interpret
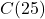 and
and 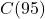 .
. - What does the vertical asymptote at
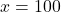 mean within the context of the problem?
mean within the context of the problem? - What percentage of the Ippizuti fish can you remove for 40000 dollars?
- Compute and interpret
- In the scenario of Example 3.2.3,
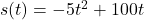 ,
, 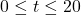 gives the height of a model rocket above the Moon’s surface, in feet,
gives the height of a model rocket above the Moon’s surface, in feet,  seconds after liftoff. For each of the times
seconds after liftoff. For each of the times 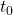 listed below, find and simplify a the formula for the average velocity
listed below, find and simplify a the formula for the average velocity 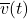 between
between  and
and 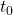 (see Definition 3.5) and use
(see Definition 3.5) and use 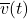 to find and interpret the instantaneous velocity of the rocket at
to find and interpret the instantaneous velocity of the rocket at 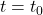 .
.
- The population of Sasquatch in Portage County
 years after the year 1803 is modeled by the function
years after the year 1803 is modeled by the function
![Rendered by QuickLaTeX.com \[P(t) = \frac{150t}{t + 15}.\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-46f0a29ecfaf4a8e8a4cf044c8956d41_l3.png)
Find and interpret the horizontal asymptote of the graph of
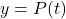 and explain what it means.
and explain what it means. - The cost in dollars,
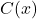 to make
to make  dOpi media players is
dOpi media players is 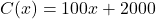 ,
, 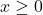 . You may wish to review the concepts of fixed and variable costs introduced in Example 1.3.8 in Section 1.3.3.
. You may wish to review the concepts of fixed and variable costs introduced in Example 1.3.8 in Section 1.3.3.
- Write a formula for the average cost
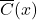 .
. - Compute and interpret
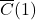 and
and 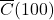 .
. - How many dOpis need to be produced so that the average cost per dOpi is 200 dollars?
- Interpret the behavior of
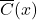 as
as 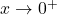 .
. - Interpret the behavior of
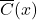 as
as 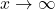 .
.
- Write a formula for the average cost
- This exercise explores the relationships between fixed cost, variable cost, and average cost. The reader is encouraged to revisit Example 1.3.8 in Section 1.3.3 as needed. Suppose the cost in dollars
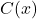 to make
to make  items is given by
items is given by 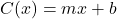 where
where 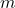 and
and  are positive real numbers.
are positive real numbers.
- Show the fixed cost (the money spent even if no items are made) is
 .
. - Show the variable cost (the increase in cost per item made) is
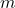 .
. - Write a formula for the average cost when making
 items,
items, 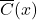 .
. - Show
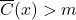 for all
for all 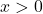 and, moreover,
and, moreover, 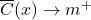 as
as 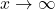 .
. - Interpret
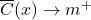 both geometrically and in terms of fixed, variable, and average costs.
both geometrically and in terms of fixed, variable, and average costs.
- Show the fixed cost (the money spent even if no items are made) is
- Suppose the price-demand function for a particular product is given by
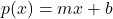 where
where  is the number of items made and sold for
is the number of items made and sold for 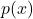 dollars. Here,
dollars. Here, 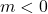 and
and 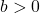 . If the cost (in dollars) to make
. If the cost (in dollars) to make  of these products is also a linear function
of these products is also a linear function 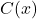 , show that the graph of the average profit function
, show that the graph of the average profit function 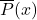 has a slant asymptote with slope
has a slant asymptote with slope 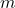 and interpret.
and interpret. - Electric circuits are built with a variable resistor. For each of the following resistance values (measured in kilo-ohms,
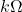 ), the corresponding power to the load (measured in milliwatts,
), the corresponding power to the load (measured in milliwatts, 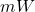 ) is given below.[19]
) is given below.[19]
![Rendered by QuickLaTeX.com \[\begin{array}{|l|r|r|r|r|r|r|} \hline \text{Resistance: }(k \Omega) & 1.012 & 2.199 & 3.275 & 4.676 & 6.805 & 9.975 \\ \hline \text{Power: }(mW) & 1.063 & 1.496 & 1.610 & 1.613 & 1.505 & 1.314 \\ \hline \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-19ff7333893648930065a58691c3be26_l3.png)
Using some fundamental laws of circuit analysis mixed with a healthy dose of algebra, we can derive the actual formula relating power
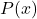 to resistance
to resistance  :
: ![Rendered by QuickLaTeX.com \[P(x) = \frac{25x}{(x + 3.9)^2}, \quad x \geq 0.\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c09b1392c6ad4ac2e6e4a0e0cddd32e9_l3.png)
- Use a graphing utility to approximate the maximum power that can be delivered to the load. What is the corresponding resistance value?
- State and interpret the end behavior of
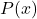 as
as 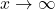 .
.
- Let
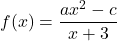 . Find values for
. Find values for  and
and  so the graph of
so the graph of  has a hole at
has a hole at 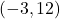 .
. - Let
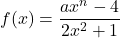 .
.
- Determine values for
 and
and  so the graph of
so the graph of  has the horizontal asymptote
has the horizontal asymptote  .
. - Determine values for
 and
and 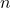 so the graph of
so the graph of 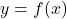 has the slant asymptote
has the slant asymptote 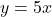 .
.
- Determine values for
- Suppose
 is a polynomial function and
is a polynomial function and  is a real number. Define
is a real number. Define 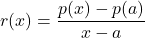 . Use the Factor Theorem, Theorem 2.10, to prove the graph of
. Use the Factor Theorem, Theorem 2.10, to prove the graph of 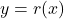 has a hole at
has a hole at  .
. - For each function
 listed below, compute the average rate of change over the indicated interval.[20] What trends do you observe? How do your answers manifest themselves graphically? How do you results compare with those of Exercise 51 in Section 2.2?
listed below, compute the average rate of change over the indicated interval.[20] What trends do you observe? How do your answers manifest themselves graphically? How do you results compare with those of Exercise 51 in Section 2.2?
![Rendered by QuickLaTeX.com \[ \begin{array}{|r||c|c|c|c|} \hline f(x) & [0.9, 1.1] & [0.99, 1.01] &[0.999, 1.001] & [0.9999, 1.0001] \\ \hline x^{-1} &&&& \\ \hline x^{-2} &&&& \\ \hline x^{-3} &&&& \\ \hline x^{-4} &&&& \\ \hline \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b054be4f5805d162f010c54cc8b67813_l3.png)
- In his now famous 1919 dissertation
 , Louis Leon Thurstone presents a rational function which models the number of words a person can type in four minutes as a function of the number of pages of practice one has completed.[21] Using his original notation and original language, we have
, Louis Leon Thurstone presents a rational function which models the number of words a person can type in four minutes as a function of the number of pages of practice one has completed.[21] Using his original notation and original language, we have 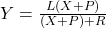 where
where 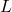 is the predicted practice limit in terms of speed units,
is the predicted practice limit in terms of speed units, 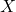 is pages written,
is pages written, 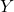 is writing speed in terms of words in four minutes,
is writing speed in terms of words in four minutes, 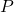 is equivalent previous practice in terms of pages and
is equivalent previous practice in terms of pages and 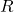 is the rate of learning. In Figure 5 of the paper, he graphs a scatter plot and the curve
is the rate of learning. In Figure 5 of the paper, he graphs a scatter plot and the curve 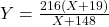 . Discuss this equation with your classmates. How would you update the notation? Explain what the horizontal asymptote of the graph means. You should take some time to look at the original paper. Skip over the computations you don’t understand yet and try to get a sense of the time and place in which the study was conducted.
. Discuss this equation with your classmates. How would you update the notation? Explain what the horizontal asymptote of the graph means. You should take some time to look at the original paper. Skip over the computations you don’t understand yet and try to get a sense of the time and place in which the study was conducted.
Section 3.2 Exercise Answers can be found in the Appendix … Coming soon
- According to this definition, all polynomial functions are also rational functions. (Take
 ). ↵
). ↵ - Technically speaking,
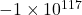 is a `small' number (because it is very far to the left on the number line.) However, it's absolute value,
is a `small' number (because it is very far to the left on the number line.) However, it's absolute value, 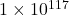 is very large. ↵
is very large. ↵ - See Exercise 23 in Section 7.3. ↵
- We are, in fact, building on Theorem 1.12 in Section 1.6, so the more you see the forest for the trees, the better off you'll be when the time comes to generalize these moves to all functions. ↵
- These functions arise in Differential Equations. The unfortunate name will make sense shortly. ↵
- Note that the rocket has already started its descent at
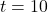 seconds (see Example 1.3.1.2 in Section 1.3.1.) However, the rocket is still at a higher altitude at when
seconds (see Example 1.3.1.2 in Section 1.3.1.) However, the rocket is still at a higher altitude at when 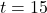 than
than 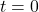 which produces a positive average velocity. ↵
which produces a positive average velocity. ↵ - Or, `How to tell your asymptote from a hole in the graph.' ↵
- In other words,
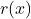 is in lowest terms. ↵
is in lowest terms. ↵ - Though the population below is more accurately modeled with the functions in Chapter 5, we approximate it (using Calculus, of course!) using a rational function. ↵
- The use of the definite article will be justified momentarily. ↵
- We will (first) encounter functions with more than one horizontal asymptote in Chapter 4.1. ↵
- Sit tight! We'll revisit this function and its end behavior shortly. ↵
- See the remarks following Theorem 3.3. ↵
- Other notations include
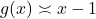 or
or 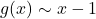 . ↵
. ↵ - Also called an `oblique' asymptote in some, ostensibly higher class (and more expensive), texts. ↵
- That's OK, though. In the next section, we'll use long division to analyze end behavior and it's worth the effort! ↵
- We generalize this result in Exercise38. ↵
- For more review, see Section 2.3. ↵
- The authors wish to thank Don Anthan and Ken White of Lakeland Community College for devising this problem and generating the accompanying data set. ↵
- See Definition 1.11 in Section 1.3.4 for a review of this concept, as needed. ↵
- This paper, which is now in the public domain and can be found here, is from a bygone era when students at business schools took typing classes on manual typewriters. ↵
A function which is the ratio of polynomial functions.
A monomial function or a function of the form f(x) = 1/x^n.
A line x = c of the graph of a function where f(x) approaches an infinity as x approaches c from one side or the other.
A line y=c of the graph of a function f(x) if as x approaches an infinity, the function approaches c.
The average rate of change of the position of an object over a span of time.
The line in which a function approaches as x goes to positive or negative infinity.
The average cost is the cost per item produced.
The profit per item sold.

