3.4 Solving Equations Involving Rational Functions
In this section, we review the solving of equations which involve rational expressions. As with equations involving numeric fractions, our first step in solving equations with algebraic fractions is to clear denominators. In doing so, we run the risk of introducing what are known as extraneous solutions – `answers’ which don’t satisfy the original equation. As we illustrate the techniques used to solve these basic equations, see if you can find the step which creates the problem for us.
Example 3.4.1
Example 3.4.1.1
Solve the following equations.
![]()
Solution:
Solve ![]() for
for ![]() .
.
Our first step is to clear the fractions by multiplying both sides of the equation by ![]() . In doing so, we are implicitly assuming
. In doing so, we are implicitly assuming ![]() ; otherwise, we would have no guarantee that the resulting equation is equivalent to our original equation.[1]
; otherwise, we would have no guarantee that the resulting equation is equivalent to our original equation.[1]
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 1 + \dfrac{1}{x} & = & x & \\ [8pt] \left(1 + \dfrac{1}{x}\right) x & = & (x)x & \text{Provided } x \neq 0 \\ [10pt] 1(x) + \dfrac{1}{x} (x) & = & x^2 & \text{Distribute} \\ [8pt] x + \dfrac{x}{x} & = & x^2 & \text{Multiply} \\ [8pt] x + 1 & = & x^2 & \\ 0 & = & x^2 - x - 1 & \text{Subtract } x \text{, subtract } 1 \\ [5pt] x & = & \dfrac{-(-1) \pm \sqrt{(-1)^2 - 4(1)(-1)}}{2(1)} & \text{Quadratic Formula} \\ x & = & \dfrac{1 \pm \sqrt{5}}{2} & \text{Simplify} \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-97b34ed2ba6cff286b762f786b7aeb22_l3.png)
We obtain two answers, ![]() . Neither of these are
. Neither of these are ![]() thus neither contradicts our assumption that
thus neither contradicts our assumption that ![]() .
.
The reader is invited to check both of these solutions.[2]
Example 3.4.1.2
Solve the following equations.
![]()
Solution:
Solve ![]() for
for ![]() .
.
To solve the equation, we clear denominators. Here, we need to assume ![]() , or
, or ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{t^3-2t+1}{t-1} & = & \dfrac{1}{2}t-1 & \\ [8pt] \left(\dfrac{t^3-2t+1}{t-1}\right) \cdot 2(t-1) & = & \left( \dfrac{1}{2}t-1 \right) \cdot 2(t-1) & \text{Provided } t \neq 1 \\ [12pt] \dfrac{(t^3-2t+1)(2\cancel{(t-1)})}{\cancel{(t-1)}} & = & \dfrac{1}{\cancel{2}} t (\cancel{2}(t-1)) - 1(2(t-1)) & \text{Multiply, distribute} \\ [8pt] 2(t^3-2t+1) & = & t^2 - t - 2t + 2 & \text{Distribute} \\ [2pt] 2t^3 - 4t + 2 & = & t^2 -3t + 2 & \text{Distribute, combine like terms} \\ [2pt] 2t^3 -t^2 - t & = & 0 & \text{Subtract } t^2 \text{, add } 3t \text{, subtract } 2\\ [2pt] t(2t^2 -t - 1) & = & 0 & \text{Factor} \\ [2pt] t = 0 & \text{or} & 2t^2 - t - 1 = 0 & \text{Zero Product Property}\\ [2pt] t = 0 & \text{or} & (2t+1)(t-1) = 0 & \text{Factor}\\ [2pt] t = 0 & \text{or} & 2t+1 = 0 \quad \text{or} \quad t-1 = 0 &\\ [2pt] t & = & 0, \; -\dfrac{1}{2} \text{ or } 1 & \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-2148e7cfd35b4518b5209bdc0590ed58_l3.png)
We assumed that ![]() in order to clear denominators. Sure enough, the candidate
in order to clear denominators. Sure enough, the candidate ![]() doesn’t check in the original equation because it causes division by
doesn’t check in the original equation because it causes division by ![]() . In this case, we call
. In this case, we call ![]() an extraneous solution. Note that
an extraneous solution. Note that ![]() does work in every equation after we clear denominators. In general, multiplying by variable expressions can produce these `extra’ solutions, which is why checking our answers is always encouraged.[3] The other two candidates,
does work in every equation after we clear denominators. In general, multiplying by variable expressions can produce these `extra’ solutions, which is why checking our answers is always encouraged.[3] The other two candidates, ![]() and
and ![]() , are solutions.
, are solutions.
Example 3.4.1.3
Solve the following equations.
![]()
Solution:
Solve ![]() for
for ![]() .
.
As before, we begin by clearing denominators. Here, we assume ![]() (so
(so ![]() ) and
) and ![]() (so
(so ![]() ).
).
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{3}{1 - w\sqrt{2}} - \dfrac{1}{2w+5} & = & 0 & \\ \left(\dfrac{3}{1 - w\sqrt{2}} - \dfrac{1}{2w+5}\right)(1 - w\sqrt{2})(2w+5) & = & 0 (1 - w\sqrt{2})(2w+5) & w \neq \dfrac{1}{\sqrt{2}}, -\dfrac{5}{2} \\ [12pt] \dfrac{3\cancel{(1 - w\sqrt{2})}(2w+5) }{\cancel{(1 - w\sqrt{2})}}- \dfrac{1(1 - w\sqrt{2})\cancel{(2w+5)}}{\cancel{(2w+5)}} & = & 0 & \text{Distribute} \\ [12pt] 3(2w+5) - (1-w\sqrt{2}) & = & 0 & \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-ad747ce5f4a317ee8dfa2c8adc141dd4_l3.png)
The result is a linear equation in ![]() so we gather the terms with
so we gather the terms with ![]() on one side of the equation and put everything else on the other. We factor out
on one side of the equation and put everything else on the other. We factor out ![]() and divide by its coefficient.
and divide by its coefficient.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 3(2w+5) - (1-w\sqrt{2}) & = & 0 & \\ 6w + 15 - 1 + w\sqrt{2} & = & 0 & \text{Distribute} \\ 6w + w\sqrt{2} & = & -14 & \text{Subtract } 14 \\ (6 + \sqrt{2})w & = & -14 & \text{Factor} \\ w & = & -\dfrac{14}{6 + \sqrt{2}} & \text{Divide by } 6 + \sqrt{2} \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-bac1b6de9a6d6fa70c2ce268ec55ec09_l3.png)
This solution is different than our excluded values, ![]() and
and ![]() , so we keep
, so we keep ![]() as our final answer.
as our final answer.
The reader is invited to check this in the original equation.
Example 3.4.1.4
Solve the following equations.
![]()
Solution:
Solve ![]() for
for ![]() .
.
To solve our next equation, we have two approaches to choose from: we could rewrite the quantities with negative exponents as fractions and clear denominators, or we can factor. We showcase each technique below.
- Clearing Denominators Approach: We rewrite the negative exponents as fractions and clear denominators. In this case, we multiply both sides of the equation by
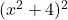 , which is never
, which is never  . (Think about that for a moment.) As a result, we need not exclude any
. (Think about that for a moment.) As a result, we need not exclude any  values from our solution set.
values from our solution set.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 3(x^2+4)^{-1} + 3x(-1)(x^2+4)^{-2}(2x) & = & 0 & \\ [8pt] \dfrac{3}{x^2+4} + \dfrac{3x(-1)(2x)}{(x^2+4)^2} & = & 0 & \text{Rewrite} \\ [12pt] \left(\dfrac{3}{x^2+4} - \dfrac{6x^2}{(x^2+4)^2} \right)(x^2+4)^2 & = & 0 (x^2+4)^2 & \text{Multiply} \\[12pt] \dfrac{3\cancelto{(x^2+4)}{(x^2 + 4)^2}}{\cancel{(x^2+4)}} - \dfrac{6x^2\cancel{(x^2+4)^2}}{\cancel{(x^2+4)^2}} & = & 0 & \text{Distribute} \\ [12pt] 3(x^2+4) - 6x^2 & = & 0 & \\ [2pt] 3x^2 + 12 - 6x^2 & = & 0 & \text{Distribute} \\ [2pt] -3x^2 & = & -12 & \text{Combine like terms, subtract } 12 \\ [2pt] x^2 & = & 4 & \text{Divide by } -3\\ [2pt] x & = & \pm \sqrt{4} = \pm 2 & \text{Extract square roots} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d52f43ac013ddc6607889da663d34e43_l3.png)
We leave it to the reader to show that both
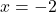 and
and 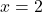 satisfy the original equation.
satisfy the original equation. - Factoring Approach: Because the equation is already set equal to
 , we’re ready to factor. Following the guidelines presented in Example 3.1.1, we factor out
, we’re ready to factor. Following the guidelines presented in Example 3.1.1, we factor out 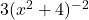 from both terms and look to see if more factoring can be done:
from both terms and look to see if more factoring can be done:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 3(x^2+4)^{-1} + 3x(-1)(x^2+4)^{-2}(2x)& = & 0 & \\ [2pt] 3(x^2+4)^{-2}( (x^2+4)^{1} + x(-1)(2x)) & = & 0 & \text{Factor} \\ [2pt] 3(x^2+4)^{-2}( x^2 + 4 - 2x^2 ) & = & 0 & \\ [2pt] 3(x^2+4)^{-2}(4 - x^2) & = & 0 & \text{Gather like terms} \\ [2pt] 3(x^2+4)^{-2} = 0 & \text{or} & 4 - x^2 = 0 & \text{Zero Product Property} \\ [2pt] \dfrac{3}{x^2+4} = 0 & \text{or} & 4 = x^2 & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-3ba80b302d8f6dd5cd12fd793c0713f3_l3.png)
The first equation yields no solutions (Think about this for a moment.) while the second gives us
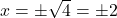 as before.
as before.
Example 3.4.1.5
Solve the following equations.
Solve ![]() for
for ![]() .
.
Solution:
Solve ![]() for
for ![]() .
.
We are asked to solve this equation for ![]() so we begin by clearing fractions with the stipulation that
so we begin by clearing fractions with the stipulation that ![]() or
or ![]() . We are left with a linear equation in the variable
. We are left with a linear equation in the variable ![]() . To solve this, we gather the terms containing
. To solve this, we gather the terms containing ![]() on one side of the equation and everything else on the other. Next, we factor out the
on one side of the equation and everything else on the other. Next, we factor out the ![]() and divide by its coefficient, which in this case turns out to be
and divide by its coefficient, which in this case turns out to be ![]() . In order to divide by
. In order to divide by ![]() , we stipulate
, we stipulate ![]() or, said differently,
or, said differently, ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{array}{rclr} $x$ & = & $\dfrac{2y+1}{y-3}$ & \\ [12pt] $x(y-3)$ & = & $\left(\dfrac{2y+1}{y-3}\right)(y-3)$ & \text{Provided } y \neq 3 \\ [12pt] $xy - 3x$ & = & $\dfrac{(2y+1)\cancel{(y-3)}}{\cancel{(y-3)}}$ & \text{Distribute, multiply} \\ [12pt] xy - 3x & = & 2y + 1 & \\ [2pt] xy - 2y & = & 3x+1 & \text{Add } 3x \text{, subtract } 2y \\ [2pt] y(x-2) & = & 3x+1 & \text{Factor} \\ [2pt] y & = & \dfrac{3x+1}{x-2} & \text{Divide provided } x \neq 2 \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-02dcd488af2883ad9e712c9d28fa7379_l3.png)
We highly encourage the reader to check the answer algebraically to see where the restrictions on ![]() and
and ![]() come into play.[4]
come into play.[4]
Example 3.4.1.6
Solve the following equations.
Solve ![]() for
for ![]() .
.
Solution:
Solve ![]() for
for ![]() .
.
Our last example comes from physics and the world of photography.[5] We take a moment here to note that while superscripts in Mathematics indicate exponents (powers), subscripts are used primarily to distinguish one or more variables. In this case, ![]() and
and ![]() are two different variables (much like
are two different variables (much like ![]() and
and ![]() ) and we treat them as such. Our first step is to clear denominators by multiplying both sides by
) and we treat them as such. Our first step is to clear denominators by multiplying both sides by ![]() – provided each is nonzero. We end up with an equation which is linear in
– provided each is nonzero. We end up with an equation which is linear in ![]() so we proceed as in the previous example.
so we proceed as in the previous example.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{1}{f} & = & \dfrac{1}{S_{1}} + \dfrac{1}{S_{2}} & \\ [12pt] \left(\dfrac{1}{f}\right)(fS_{1}S_{2}) & = & \left(\dfrac{1}{S_{1}} + \dfrac{1}{S_{2}}\right) (fS_{1}S_{2}) & \text{Provided } f \neq 0, S_{1} \neq 0, S_{2}\neq 0 \\ [12pt] \dfrac{fS_{1}S_{2}}{f} & = & \dfrac{fS_{1}S_{2}}{S_{1}} + \dfrac{fS_{1}S_{\text{\tiny $2$}}}{S_{2}} & \text{Multiply, distribute} \\ [12pt] \dfrac{\cancel{f}S_{1}S_{2}}{\cancel{f}} & = & \dfrac{f\cancel{S_{1}}S_{\text{\tiny $2$}}}{\cancel{S_{1}}} + \dfrac{fS_{1}\cancel{S_{2}}}{\cancel{S_{2}}} & \text{Divide out} \\ [12pt] S_{1}S_{2} & = & f S_{2} + fS_{1} & \\ [3pt] S_{1}S_{2} - fS_{1} & = & f S_{2} & \text{Subtract } fS_{1} \\ [3pt] S_{1}(S_{2} - f) & = & f S_{2} & \text{Factor} \\ [5pt] S_{1} & = & \dfrac{f S_{2}}{S_{2} - f} & \text{Divide provided } S_{2} \neq f \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b0139f4ec55cc39ba80f80780c4f6653_l3.png)
As always, the reader is highly encouraged to check the answer.[6]
3.4.1 Section Exercises
In Exercises 1 – 9, determine all real solutions. Be sure to check for extraneous solutions.
In Exercises 10 – 12, use Theorem 0.4 along with the techniques in this section to determine all real solutions.
In Exercises 13 – 15, compute all real solutions.
In Exercises 16 – 21, solve the given equation for the indicated variable.
- Solve for
 :
: 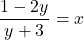
- Solve for
 :
: 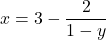
- Solve[7] for
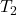 :
: 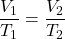
- Solve for
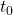 :
: 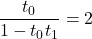
- Solve for
 :
: 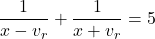
- Solve for
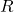 :
: 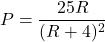
Section 3.4 Exercise Answers can be found in the Appendix … Coming soon
- See Section 0.5. ↵
- The check relies on being able to `rationalize' the denominator - a skill we haven't reviewed yet. Additionally, the positive solution to this equation is the famous Golden Ratio. ↵
- Contrast this with what happened in Example 0.5.3 when we divided by a variable and `lost' a solution. ↵
- It involves simplifying a compound fraction! ↵
- See this article on focal length. ↵
 and see what the restriction
and see what the restriction 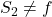 means in terms of focusing a camera! ↵
means in terms of focusing a camera! ↵- Recall: subscripts on variables have no intrinsic mathematical meaning; they're just used to distinguish one variable from another. In other words, treat quantities like `
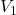 ' and `
' and `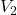 ' as two different variables as you would `
' as two different variables as you would ` ' and `
' and ` .' ↵
.' ↵

