6.1 Solving Systems of Linear Equations
This section combines ideas from Section 0.5 and 1.3.1 so that we can start to solve systems of linear equations. Before we get ahead of ourselves, let’s review a few definitions.
Definition 6.1
A linear equation in two variables is an equation of the form ![]() where
where ![]() ,
, ![]() and
and ![]() are real numbers and at least one of
are real numbers and at least one of ![]() and
and ![]() is nonzero.
is nonzero.
We are using subscripts in Definition 6.1 to indicate different, but fixed, real numbers and those subscripts have no mathematical meaning beyond that. For example, ![]() is a linear equation in two variables with
is a linear equation in two variables with ![]() ,
, ![]() and
and ![]() . We can also consider
. We can also consider ![]() to be a linear equation in two variables[1] by identifying
to be a linear equation in two variables[1] by identifying ![]() ,
, ![]() , and
, and ![]() .
.
If ![]() and
and ![]() are both
are both ![]() , then depending on
, then depending on ![]() , we get either an equation which is always true, called an identity, or an equation which is never true, called a contradiction. (If
, we get either an equation which is always true, called an identity, or an equation which is never true, called a contradiction. (If ![]() , then we get
, then we get ![]() , which is always true. If
, which is always true. If ![]() , then we’d have
, then we’d have ![]() , which is never true.) Even though identities and contradictions will a large role to play throughout this Chapter, we do not consider them linear equations. The key to identifying linear equations is to note that the variables involved are to the first power and that the coefficients of the variables are numbers. Some examples of equations which are non-linear are
, which is never true.) Even though identities and contradictions will a large role to play throughout this Chapter, we do not consider them linear equations. The key to identifying linear equations is to note that the variables involved are to the first power and that the coefficients of the variables are numbers. Some examples of equations which are non-linear are ![]() ,
, ![]() and
and ![]() . The reader should consider why these do not satisfy Definition 6.1.
. The reader should consider why these do not satisfy Definition 6.1.
We know from our work is Sections 1.3.1 that the graphs of linear equations are lines. If we couple two or more linear equations together, in effect to find the points of intersection of two or more lines, we obtain a system of linear equations in two variables.
While some linear systems have one solution (one intersection point) , some linear systems may not have a solution (no points of intersection) and others may have an infinite number of solutions (infinitely many points of intersection).
In addition to considering the number of equations and variables, we can categorize systems of linear equations by the number of solutions.
- A consistent system of equations has at least one solution.
- A consistent system is considered to be an independent system if it has a single solution, such as the example we just explored. The two lines have different slopes (
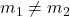 ) and intersect at one point in the plane.
) and intersect at one point in the plane. - A consistent system is considered to be a dependent system if the equations have the same slope and the same
 -coordinate of the
-coordinate of the  -intercept (
-intercept (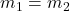 and
and 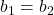 ). In other words, the lines coincide so the equations represent the same line. Every point on the line represents a coordinate pair that satisfies the system. Thus, there are an infinite number of solutions.
). In other words, the lines coincide so the equations represent the same line. Every point on the line represents a coordinate pair that satisfies the system. Thus, there are an infinite number of solutions.
- A consistent system is considered to be an independent system if it has a single solution, such as the example we just explored. The two lines have different slopes (
- An inconsistent system is when the equations represent two parallel lines, where the lines have the same slope and different
 -coordinates of the
-coordinates of the  -intercepts (
-intercepts (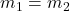 and
and 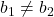 ). There are no points common to both lines; hence, there is no solution to the system.
). There are no points common to both lines; hence, there is no solution to the system.
In this section we will use three techniques to solving a system of linear equations.
- Graphical
- Substitution
- Elimination
Let’s consider the two algebraic methods of Substitution and Elimination. In the method of Substitution we solve one of the equations for one of the variables and then substitute the results into the second equation to solve for the remaining variable.
Substitution Method
- Solve one equation for one of the variables.
- Substitute the result into the second equation to solve for the remaining variable, if possible.
- Then substitute the result of Step 2 back into the equation found in Step 1, and solve for the variable value not known.
In the second algebraic method, Elimination, we use addition and multiplication to combine the two equations into a single equation of one variable, thus eliminating one variable.
Elimination Method
- Write both equations so the variable terms are on the left-hand side and the constant term is on the right-hand side of the equals sign.
- Multiply one or both equations by the necessary constants so that coefficients of one of the variables are the same, but have opposite signs (additive inverses).
- Add the two equations; the resulting equation should have at most one variable.
- Solve the resulting equation from Step 3 for the remaining variable, if one exists.
- Substitute the result of Step 4 back into one of the original equations and solve for the variable value not known.
Our first example explores these basic techniques for solving these systems. Remember – if we are looking for points in the plane, then both the ![]() and
and ![]() values are important. This is a key distinction between solving one equation and solving a system of equations.
values are important. This is a key distinction between solving one equation and solving a system of equations.
Example 6.1.1
Example 6.1.1.1
Solve the following systems of equations. Check your answer algebraically and graphically. (Said another way, make sure both ![]() and
and ![]() are correct!)
are correct!)
![]()
Solution:
Solve the system ![]()
Our first system is nearly solved for us. The second equation tells us that ![]() . To find the corresponding value of
. To find the corresponding value of ![]() , we substitute this value for
, we substitute this value for ![]() into the the first equation to obtain
into the the first equation to obtain ![]() , so that
, so that ![]() .
.
Our solution to the system is ![]() .
.
To check this algebraically, we substitute ![]() and
and ![]() into each equation and see that they are satisfied. We see
into each equation and see that they are satisfied. We see ![]() , and
, and ![]() , as required. To check our answer graphically, we graph the lines
, as required. To check our answer graphically, we graph the lines ![]() and
and ![]() and verify that they intersect at
and verify that they intersect at ![]() .
.
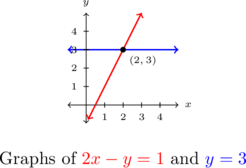
Example 6.1.1.2
Solve the following systems of equations. Check your answer algebraically and graphically. (Said another way, make sure both ![]() and
and ![]() are correct!)
are correct!)
![]()
Solution:
Solve the system ![]()
To solve the second system, we use the elimination method to eliminate the variable ![]() . We take the two equations as given and `add equals to equals’ to obtain
. We take the two equations as given and `add equals to equals’ to obtain
![Rendered by QuickLaTeX.com \[ \begin{array}{lrcr} & 3x+4y & = & -2 \\ + & (-3x-y & = & 5 ) \\ \hline & 3y & = & 3\end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a591f09b926f96a9bc1b84b29c1123d3_l3.png)
This gives us ![]() . We now substitute
. We now substitute ![]() into either of the two equations, say
into either of the two equations, say ![]() , to get
, to get ![]() so that
so that ![]() .
.
Our solution is ![]() .
.
Substituting ![]() and
and ![]() into the first equation gives
into the first equation gives ![]() , which is true, and, likewise, when we check
, which is true, and, likewise, when we check ![]() in the second equation, we get
in the second equation, we get ![]() , which is also true. Geometrically, the lines
, which is also true. Geometrically, the lines ![]() and
and ![]() intersect at
intersect at ![]() .
.
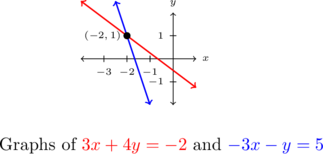
Example 6.1.1.3
Solve the following systems of equations. Check your answer algebraically and graphically. (Said another way, make sure both ![]() and
and ![]() are correct!)
are correct!)
![Rendered by QuickLaTeX.com \left\{ \begin{array}{rcr} \frac{x}{3} -\frac{4y}{5} & = & \frac{7}{5} \\ [3pt] \frac{2x}{9} + \frac{y}{3} & = & \frac{1}{2} \\ \end{array} \right.](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-8cfd3349cd42e9bc7daffc8799cab491_l3.png)
Solution:
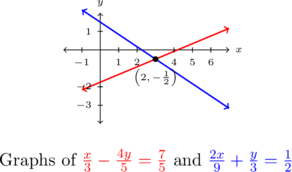
Solve the system ![Rendered by QuickLaTeX.com \left\{ \begin{array}{rcr} \frac{x}{3} -\frac{4y}{5} & = & \frac{7}{5} \\ [3pt] \frac{2x}{9} + \frac{y}{3} & = & \frac{1}{2} \\ \end{array} \right.](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-8cfd3349cd42e9bc7daffc8799cab491_l3.png)
The equations in the third system are more approachable if we clear denominators. We multiply both sides of the first equation by ![]() and both sides of the second equation by
and both sides of the second equation by ![]() to obtain the kinder, gentler system
to obtain the kinder, gentler system
![]()
Adding these two equations directly fails to eliminate either of the variables, but we note that if we multiply the first equation by ![]() and the second by
and the second by ![]() , we will be in a position to eliminate the
, we will be in a position to eliminate the ![]() term
term
![Rendered by QuickLaTeX.com \[ \begin{array}{lrcr} & 20x-48y & = & 84 \\ + & (-20x-30y & = & -45 ) \\ \hline & -78y & = & 39\end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4846e03ded19e6e79032ccdf9c40d3f1_l3.png)
From this we get ![]() . We can temporarily avoid too much unpleasantness by choosing to substitute
. We can temporarily avoid too much unpleasantness by choosing to substitute ![]() into one of the equivalent equations we found by clearing denominators, say into
into one of the equivalent equations we found by clearing denominators, say into ![]() . We get
. We get ![]() which gives
which gives ![]()
Our answer is ![]() .
.
At this point, we have no choice; in order to check an answer algebraically, we must see if the answer satisfies both of the original equations, so we substitute ![]() and
and ![]() into both
into both ![]() and
and ![]() . We leave it to the reader to verify that the solution is correct. Graphing both of the lines involved with considerable care yields an intersection point of
. We leave it to the reader to verify that the solution is correct. Graphing both of the lines involved with considerable care yields an intersection point of ![]() .
.
Example 6.1.1.4
Solve the following systems of equations. Check your answer algebraically and graphically. (Said another way, make sure both ![]() and
and ![]() are correct!)
are correct!)
![]()
Solution:
Solve the system ![]()
An eerie calm settles over us as we cautiously approach our fourth system. Do its friendly integer coefficients belie something more sinister? We note that if we multiply both sides of the first equation by ![]() and both sides of the second equation by
and both sides of the second equation by ![]() , we are ready to eliminate the
, we are ready to eliminate the ![]()
![Rendered by QuickLaTeX.com \[ \begin{array}{lrcr} & 6x-12y & = & 18 \\ + & (-6x+12y & = & -18 ) \\ \hline & 0 & = & 0\end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-45497cfb7c2c1f27bf058e6045ea199e_l3.png)
We eliminated not only the ![]() , but the
, but the ![]() as well and we are left with the identity
as well and we are left with the identity ![]() . This means that these two different linear equations are, in fact, equivalent. In other words, if an ordered pair
. This means that these two different linear equations are, in fact, equivalent. In other words, if an ordered pair ![]() satisfies the equation
satisfies the equation ![]() , it automatically satisfies the equation
, it automatically satisfies the equation ![]() .
.
This system has infinitely many solutions and one way to describe the solution set to this system is to use the roster method[2] and write ![]() . While this is correct (and corresponds exactly to what’s happening graphically, as we shall see shortly), we take this opportunity to introduce the notion of a parametric solution to a system.
. While this is correct (and corresponds exactly to what’s happening graphically, as we shall see shortly), we take this opportunity to introduce the notion of a parametric solution to a system.
Our first step is to solve ![]() for one of the variables, say
for one of the variables, say ![]() . For each value of
. For each value of ![]() , the formula
, the formula ![]() determines the corresponding
determines the corresponding ![]() -value of a solution. As we have no restriction on
-value of a solution. As we have no restriction on ![]() , it is called a free variable. We let
, it is called a free variable. We let ![]() , a so-called `parameter’, and get
, a so-called `parameter’, and get ![]() .
.
Our set of solutions can then be described as ![]() .[3]
.[3]
For specific values of ![]() , we can generate solutions. For example,
, we can generate solutions. For example, ![]() gives us the solution
gives us the solution ![]() ;
; ![]() gives us
gives us ![]() , and while we can check that each of these particular solutions satisfy both equations, the question is how do we check our general answer algebraically? Same as always.
, and while we can check that each of these particular solutions satisfy both equations, the question is how do we check our general answer algebraically? Same as always.
We claim that for any real number ![]() , the pair
, the pair ![]() satisfies both equations. Substituting
satisfies both equations. Substituting ![]() and
and ![]() into
into ![]() gives
gives ![]() . Simplifying, we get
. Simplifying, we get ![]() , which is always true. Similarly, when we make these substitutions in the equation
, which is always true. Similarly, when we make these substitutions in the equation ![]() , we get
, we get ![]() which reduces to
which reduces to ![]() , so it checks out, too.
, so it checks out, too.
Geometrically, ![]() and
and ![]() are the same line, which means that they intersect at every point on their graphs. The reader is encouraged to think about how our parametric solution says exactly that.
are the same line, which means that they intersect at every point on their graphs. The reader is encouraged to think about how our parametric solution says exactly that.
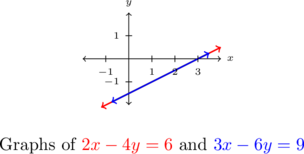
Example 6.1.1.5
Solve the following systems of equations. Check your answer algebraically and graphically. (Said another way, make sure both ![]() and
and ![]() are correct!)
are correct!)
![]()
Solution:
Solve the system ![]()
Multiplying both sides of the first equation by ![]() and the both sides of the second equation by
and the both sides of the second equation by ![]() , we set the stage to eliminate
, we set the stage to eliminate ![]()
![Rendered by QuickLaTeX.com \[ \begin{array}{lrcr} & 12x + 6y & = & 18 \\ + & (-12x-6y & = & -36 ) \\ \hline & 0 & = & -18 \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-fd5d6a35a0af1da8dc62fe9683b1aa84_l3.png)
As in the previous example, both ![]() and
and ![]() dropped out of the equation, but we are left with an irrevocable contradiction,
dropped out of the equation, but we are left with an irrevocable contradiction, ![]() .
.
This tells us that it is impossible to find a pair ![]() which satisfies both equations; in other words, the system has no solution.
which satisfies both equations; in other words, the system has no solution.
Graphically, the lines ![]() and
and ![]() are distinct and parallel, so they do not intersect.
are distinct and parallel, so they do not intersect.
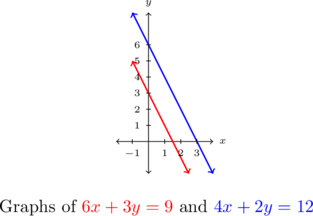
Example 6.1.1.6
Solve the following systems of equations. Check your answer algebraically and graphically. (Said another way, make sure both ![]() and
and ![]() are correct!)
are correct!)
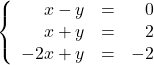
Solution:
Solve the system 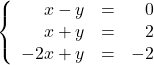
We can begin to solve our last system by adding the first two equations
![Rendered by QuickLaTeX.com \[ \begin{array}{lrcr} & x - y & = & 0 \\ + & (x + y & = & 2 ) \\ \hline & 2x & = & 2 \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-91f015ec303d9966b9c88cdd9a0e5a51_l3.png)
which gives ![]() . Substituting this into the first equation gives
. Substituting this into the first equation gives ![]() so that
so that ![]() .
.
We seem to have determined a solution to our system, ![]() . While this checks in the first two equations, when we substitute
. While this checks in the first two equations, when we substitute ![]() and
and ![]() into the third equation, we get
into the third equation, we get ![]() which simplifies to the contradiction
which simplifies to the contradiction ![]() .
.
Graphing the lines ![]() ,
, ![]() , and
, and ![]() , we see that the first two lines do, in fact, intersect at
, we see that the first two lines do, in fact, intersect at ![]() , however, all three lines never intersect at the same point simultaneously, which is what is required if a solution to the system is to be found.
, however, all three lines never intersect at the same point simultaneously, which is what is required if a solution to the system is to be found.
Thus, we say the system has no solution.

A few remarks about Example 6.1.1 are in order. We classify numbers 1, 2 and 3 in Example 6.1.1 as consistent independent systems, number 4 is consistent dependent, and numbers 5 and 6 are inconsistent.[4] The system in 6 above is called overdetermined, because we have more equations than variables.[5] Not surprisingly, a system with more variables than equations is called underdetermined. While the system in number 6 above is overdetermined and inconsistent, there exist overdetermined consistent systems (both dependent and independent) and we leave it to the reader to think about what is happening algebraically and geometrically in these cases. Likewise, there are both consistent and inconsistent underdetermined systems,[6] but a consistent underdetermined system of linear equations is necessarily dependent.[7]
We end this section with a story problem. It is an example of a classic “mixture” problem and should be familiar to most readers. The basic goal here is to create two equations: one which represents
![]()
and the other which represents
![]()
Example 6.1.2
Example 6.1.2
The Dude-Bros want to create a highly caffeinated, yet still drinkable, fruit punch for their annual “Disturb the Neighbors BBQ and Dance Competition”. They plan to add Sasquatch Sweat![]() Energy Drink, which has 100 mg of caffeine per fluid ounce, to Frooty Giggle Delight
Energy Drink, which has 100 mg of caffeine per fluid ounce, to Frooty Giggle Delight![]() , which has only 3 mg of caffeine per fluid ounce. How much of each component is required to make 5 gallons[8] of a fruit punch that has 80 mg of caffeine per fluid ounce.
, which has only 3 mg of caffeine per fluid ounce. How much of each component is required to make 5 gallons[8] of a fruit punch that has 80 mg of caffeine per fluid ounce.
Solution:
Let ![]() stand for the number of fluid ounces of Sasquatch Sweat
stand for the number of fluid ounces of Sasquatch Sweat![]() Energy Drink and let
Energy Drink and let ![]() be the number of fluid ounces of Frooty Giggle Delight
be the number of fluid ounces of Frooty Giggle Delight![]() that will be added together. The goal is to make 5 gallons and there are 128 fluid ounces per gallon so the first equation is
that will be added together. The goal is to make 5 gallons and there are 128 fluid ounces per gallon so the first equation is
![]()
That equation describes “stuff + other stuff = total stuff” measured in fluid ounces. Now we need to consider the value of the stuff – in this case we need to see how much caffeine is being contributed by each component. Each fluid ounce of Sasquatch Sweat![]() contains 100 mg of caffeine so
contains 100 mg of caffeine so ![]() fluid ounces would contain
fluid ounces would contain ![]() mg of caffeine.
mg of caffeine.
Similarly, the ![]() fluid ounces of Frooty Giggle Delight
fluid ounces of Frooty Giggle Delight![]() add
add ![]() mg of caffeine to the total mixture. Thus when we go to express “value of stuff + value of other stuff = value of total stuff” we need to figure out how much caffeine is supposed to be in the end product. Well, the goal was 5 gallons of punch that had 80 mg of caffeine per fluid ounce so the Dude-Bros need to end up with
mg of caffeine to the total mixture. Thus when we go to express “value of stuff + value of other stuff = value of total stuff” we need to figure out how much caffeine is supposed to be in the end product. Well, the goal was 5 gallons of punch that had 80 mg of caffeine per fluid ounce so the Dude-Bros need to end up with ![]() mg of caffeine when they’re done. Hence the second is equation is
mg of caffeine when they’re done. Hence the second is equation is
![]()
By turning the first equation into ![]() and substituting that into the second equation we get
and substituting that into the second equation we get
![]()
which yields ![]() fluid ounces. Back-substituting this value of
fluid ounces. Back-substituting this value of ![]() into the first equation gives us
into the first equation gives us ![]() fluid ounces.
fluid ounces.
The reader should take the time to verify that ![]() and
and ![]() do indeed satisfy both equations and thus are the solution to the problem. Those are fairly unattractive numbers so we end this example by discussing a way to verify an approximate answer which is reasonable without having to fight with fractions. Round
do indeed satisfy both equations and thus are the solution to the problem. Those are fairly unattractive numbers so we end this example by discussing a way to verify an approximate answer which is reasonable without having to fight with fractions. Round ![]() down to 508 and round
down to 508 and round ![]() up to 132. Clearly
up to 132. Clearly ![]() so the first equation is still satisfied. Notice that
so the first equation is still satisfied. Notice that ![]() which is really close to 51200. Thus the second equation is nearly satisfied which means the values
which is really close to 51200. Thus the second equation is nearly satisfied which means the values ![]() and
and ![]() , while not precise, are reasonable.[9]
, while not precise, are reasonable.[9]
6.1.1 Section Exercises
In Exercises 1 – 8, solve the given system using substitution and/or elimination. Classify each system as consistent independent, consistent dependent, or inconsistent. Check your answers both algebraically and graphically.
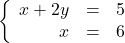
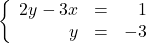
![Rendered by QuickLaTeX.com \left\{ \begin{array}{rcr} \frac{x+2y}{4} & = & -5 \\[5pt] \frac{3x-y}{2} & = & 1 \end{array} \right.](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-3c1b806628c62bea3045188421f61c08_l3.png)
![Rendered by QuickLaTeX.com \left\{ \begin{array}{rcr} \frac{2}{3} x-\frac{1}{5}y & = & 3 \\[5pt] \frac{1}{2}x+\frac{3}{4}y& = & 1 \end{array} \right.](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b26e1437605ddbdd6d408a9d278be6ea_l3.png)
![Rendered by QuickLaTeX.com \left\{ \begin{array}{rcr} \frac{1}{2}x-\frac{1}{3}y & = & -1 \\ [5pt] 2y-3x & = & 6 \end{array} \right.](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-352c60a434ed2a6faea3f89af125d566_l3.png)
![Rendered by QuickLaTeX.com \left\{ \begin{array}{rcr} x+4y & = & 6 \\ [5pt] \frac{1}{12}x+\frac{1}{3}y& = & \frac{1}{2} \end{array} \right.](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-bab8c103ea3b6bde9d8e0d183d5b9cfe_l3.png)
![Rendered by QuickLaTeX.com \left\{ \begin{array}{rcr} 3y-\frac{3}{2}x & = & -\frac{15}{2} \\ [5pt] \frac{1}{2}x-y & = & \frac{3}{2} \end{array} \right.](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c354d9fa43f434cd5e1c9d300fb7f640_l3.png)
![Rendered by QuickLaTeX.com \left\{ \begin{array}{rcr} \frac{5}{6}x+\frac{5}{3}y & = & -\frac{7}{3} \\ [5pt] -\frac{10}{3}x-\frac{20}{3}y & = & 10 \end{array} \right.](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7a50630a75292f035a047a7eb5178514_l3.png)
- A local buffet charges
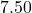 per person for the basic buffet and
per person for the basic buffet and 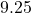 for the deluxe buffet (which includes crab legs.) If 27 diners went out to eat and the total bill was
for the deluxe buffet (which includes crab legs.) If 27 diners went out to eat and the total bill was 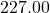 before taxes, how many chose the basic buffet and how many chose the deluxe buffet?
before taxes, how many chose the basic buffet and how many chose the deluxe buffet? - At The Old Home Fill’er Up and Keep on a-Truckin’ Cafe, Mavis mixes two different types of coffee beans to produce a house blend. The first type costs $3 per pound and the second costs $8 per pound. How much of each type does Mavis use to make 50 pounds of a blend which costs $6 per pound?
- Skippy has a total of
 10,000 to split between two investments. One account offers
10,000 to split between two investments. One account offers 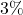 simple interest, and the other account offers
simple interest, and the other account offers 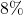 simple interest. For tax reasons, he can only earn
simple interest. For tax reasons, he can only earn 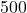 in interest the entire year. How much money should Skippy invest in each account to earn
in interest the entire year. How much money should Skippy invest in each account to earn 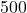 in interest for the year?
in interest for the year? - A
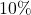 salt solution is to be mixed with pure water to produce 75 gallons of a
salt solution is to be mixed with pure water to produce 75 gallons of a 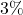 salt solution. How much of each are needed?
salt solution. How much of each are needed? - This exercise is a follow-up to Example 6.1.2. Work with your classmates to explain why mixing 4 gallons of Sasquatch Sweat
 Energy Drink and 1 gallon of Frooty Giggle Delight
Energy Drink and 1 gallon of Frooty Giggle Delight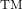 would also produce a mixture that was “close enough for the Dude-Bros”.
would also produce a mixture that was “close enough for the Dude-Bros”.
Section 6.1 Exercise Answers can be found in the Appendix … Coming soon
- Critics may argue that
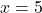 is clearly an equation in one variable. It can also be considered an equation in 117 variables with the coefficients of 116 variables set to
is clearly an equation in one variable. It can also be considered an equation in 117 variables with the coefficients of 116 variables set to  . As with many conventions in Mathematics, the context will clarify the situation. ↵
. As with many conventions in Mathematics, the context will clarify the situation. ↵ - See Section0.4 for a review of this. ↵
- Note that we could have just as easily chosen to solve
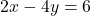 for
for  to obtain
to obtain 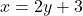 . Letting
. Letting  be the parameter
be the parameter  , we have that for any value of
, we have that for any value of  ,
, 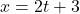 , which gives
, which gives 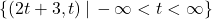 . There is no one correct way to parameterize the solution set, which is why it is always best to check your answer. ↵
. There is no one correct way to parameterize the solution set, which is why it is always best to check your answer. ↵ - The adjectives `dependent' and `independent' apply only to consistent systems -- they describe the type of solutions. Is there a free variable (dependent) or not (independent)? ↵
- If we think if each variable being an unknown quantity, then ostensibly, to recover two unknown quantities, we need two pieces of information - i.e., two equations. Having more than two equations suggests we have more information than necessary to determine the values of the unknowns. While this is not necessarily the case, it does explain the choice of terminology `overdetermined'. ↵
- We need more than two variables to give an example of the latter. ↵
- Again, experience with systems with more variables helps to see this here, as does a solid course in Linear Algebra. ↵
- Warning: unit conversion ahead! ↵
- Just be careful here - sometimes ``close enough for the Dude-Bros'' is not good enough for your Professor! ↵
An equation where the powers of both variables is 1 and the coefficients of the variables are nonzero.

