6.2 Solving Systems of Nonlinear Equations
In this section, we study systems of non-linear equations. In non-linear equations, we can have variables raised to powers other than ![]() , different variables multiplied together, or variables can occur as arguments of exponential and logarithmic functions.
, different variables multiplied together, or variables can occur as arguments of exponential and logarithmic functions.
Unlike the systems of linear equations for which we have developed several algorithmic solution techniques, there is no general algorithm to solve systems of non-linear equations. Moreover, all of the usual hazards of non-linear equations like extraneous solutions and domain restrictions are once again present.
Along with the tried and true techniques of Substitution and Elimination, we shall often need equal parts tenacity and ingenuity to see a problem through to the end. You may find it necessary to review topics throughout the text which pertain to solving equations involving the various functions we have studied thus far. To get the section rolling we begin with a fairly routine example.
Example 6.2.1
Example 6.2.1.1
Solve the following systems of equations. Verify answers algebraically and graphically.
![]()
Solution:
Solve the system ![]()
Both equations contain ![]() and
and ![]() only, so we can use elimination as seen in Section 6.1. We multiply both sides of the first equation by
only, so we can use elimination as seen in Section 6.1. We multiply both sides of the first equation by ![]() and then add the two equations together.
and then add the two equations together.
![Rendered by QuickLaTeX.com \[ \begin{array}{lrcr} & -4x^2 -4y^2 & = & -16 \\ + & (4x^2+9y^2 & = & 36 ) \\ \hline & 5y^{2} & = & 20\end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-75d56585dc93896416cfd2117ab35248_l3.png)
From ![]() , we get
, we get ![]() or
or ![]() .
.
To find the associated ![]() values, we substitute each value of
values, we substitute each value of ![]() into one of the equations to find the resulting value of
into one of the equations to find the resulting value of ![]() . Choosing
. Choosing ![]() , we find that for both
, we find that for both ![]() and
and ![]() , we get
, we get ![]()
Our solution is thus ![]() .
.
To verify these answers algebraically, we would need to show that the pair ![]() and
and ![]() each satisfy both equations. We leave this to the reader.
each satisfy both equations. We leave this to the reader.
We see from the graph that the two curves intersect at their ![]() -intercepts only,
-intercepts only, ![]() .
.

Example 6.2.1.2
Solve the following systems of equations. Verify answers algebraically and graphically.
![]()
Solution:
Solve the system ![]()
We proceed as before to eliminate one of the variables. Again we will multiply both sides of the first equation by ![]() and add the resulting equation to the second.
and add the resulting equation to the second.
![Rendered by QuickLaTeX.com \[ \begin{array}{lrcr} & -4x^2 -4y^2 & = & -16 \\ + & (4x^2-9y^2 & = & 36 ) \\ \hline & -13y^{2} & = & 20\end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-669f7953c332216c3c5f14b415aae4b2_l3.png)
Because the equation ![]() admits no real solution, the system is inconsistent.
admits no real solution, the system is inconsistent.
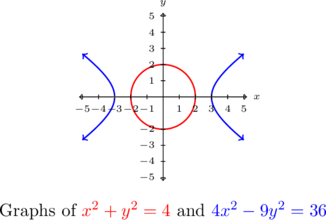
To verify this graphically, we note that ![]() is the same circle as before, but when writing the second equation in standard form,
is the same circle as before, but when writing the second equation in standard form, ![]() , we find a hyperbola centered at
, we find a hyperbola centered at ![]() opening to the left and right with a transverse axis of length
opening to the left and right with a transverse axis of length ![]() and a conjugate axis of length
and a conjugate axis of length ![]() .
.
We see that the circle and the hyperbola have no points in common, hence, there are no solutions.
Example 6.2.1.3
Solve the following systems of equations. Verify answers algebraically and graphically.
![]()
Solution:
Solve the system ![]()
There are no like terms among the two equations, thus elimination won’t work here. Instead, we proceed using substitution.
From the equation ![]() , we get
, we get ![]() . Substituting this into
. Substituting this into ![]() gives
gives ![]() . Solving, we find
. Solving, we find ![]() or
or ![]() .
.
Returning to the equation we used for the substitution, ![]() , we find
, we find ![]() when
when ![]() , so one solution is
, so one solution is ![]() and the other is
and the other is ![]() .
.
Hence, our final answer is ![]() .
.
As before, we leave the algebraic check to the reader.
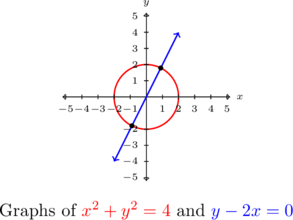
The graph of ![]() is our circle from before and the graph of
is our circle from before and the graph of ![]() , or
, or ![]() is a line through the origin with slope
is a line through the origin with slope ![]() . Even though we cannot easily verify the numerical values of the points of intersection from our sketch, we can be sure there are just two solutions: one in Quadrant I and one in Quadrant III. This observation, combined with our (your) algebraic check gives us confidence our solution is correct.[1]
. Even though we cannot easily verify the numerical values of the points of intersection from our sketch, we can be sure there are just two solutions: one in Quadrant I and one in Quadrant III. This observation, combined with our (your) algebraic check gives us confidence our solution is correct.[1]
Example 6.2.1.4
Solve the following systems of equations. Verify answers algebraically and graphically.
![]()
Solution:
Solve the system ![]()
While it may be tempting to solve ![]() as
as ![]() and substitute, we note that this system is set up for elimination.[2]
and substitute, we note that this system is set up for elimination.[2]
![Rendered by QuickLaTeX.com \[ \begin{array}{lrcr} & x^2 +y^2 & = & 4 \\ + & (-x^2+y & = & 0 ) \\ \hline & y^{2} + y & = & 4 \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e9ca813e0f5a85835d5d79156a3c49c3_l3.png)
From ![]() we get
we get ![]() which gives
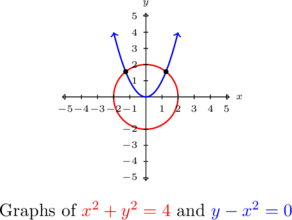
which gives ![]() . Due to the complicated nature of these answers, it is worth our time to make a quick sketch of both equations first to head off any extraneous solutions we may encounter.
. Due to the complicated nature of these answers, it is worth our time to make a quick sketch of both equations first to head off any extraneous solutions we may encounter.
We see that the circle ![]() intersects the parabola
intersects the parabola ![]() exactly twice, and both of these points have a positive
exactly twice, and both of these points have a positive ![]() value.
value.
Of the two solutions for ![]() , only
, only ![]() is positive, so to get our solution, we substitute this into
is positive, so to get our solution, we substitute this into ![]() and solve for
and solve for ![]() . We get
. We get ![]() .
.
Our final answer is ![]() .
.
Checking these answers algebraically amounts to a true test of anyone’s algebraic mettle and as such is left to the reader.
A couple of remarks about Example 6.2.1 are in order. First note that, unlike systems of linear equations, it is possible for a system of non-linear equations to have more than one solution without having infinitely many solutions. In fact, while we characterize systems of nonlinear equations as being `consistent’ or `inconsistent,’ we generally don’t use the labels `dependent’ or `independent’.
Secondly, as we saw with the last problem, sometimes making a quick sketch of the problem situation can save a lot of time and effort. While in general the curves in a system of non-linear equations may not be easily visualized, it pays to take advantage when they are.
6.2.1 Section Exercises
In Exercises 1 – 6, solve the given system of nonlinear equations. Sketch the graph of both equations on the same set of axes to verify the solution set.
In Exercises 7 – 14, solve the given system of nonlinear equations. Use a graph to help you avoid any potential extraneous solutions.
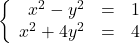
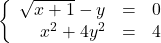
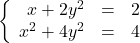
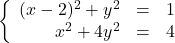
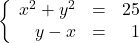
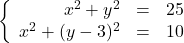
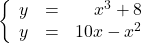
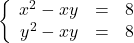
- A certain bacteria culture follows the Law of Uninhibited Growth, Equation 5.4. After 10 minutes, there are 10,000 bacteria. Five minutes later, there are 14,000 bacteria. How many bacteria were present initially? How long before there are 50,000 bacteria?
- Consider the system of nonlinear equations below
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{rcr} \dfrac{4}{x} + \dfrac{3}{y} & = & 1 \\[10pt] \dfrac{3}{x} + \dfrac{2}{y} & = & -1 \\ \end{array} \right.\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e4ecd1e78651e43dbd80446251a170d0_l3.png)
If we let
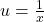 and
and 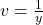 then the system becomes
then the system becomes ![Rendered by QuickLaTeX.com \[\left\{\begin{array}{rcr} 4u + 3v & = & 1 \\ 3u + 2v & = & -1 \\ \end{array} \right.\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d7f121fd20ef62211fc215dcc7b0b02a_l3.png)
This associated system of linear equations can then be solved using any of the techniques presented earlier in the chapter to find that
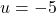 and
and 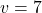 . Thus
. Thus 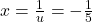 and
and 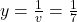 .
.
We say that the original system is linear in form because its equations are not linear but a few substitutions reveal a structure that we can treat like a system of linear equations. The system below is linear in form. Make the appropriate substitutions and solve for and
and  .
. ![Rendered by QuickLaTeX.com \[ \left\{\begin{array}{rcr} 4x^{3} + 3\sqrt{y} & = & 1 \\ 3x^{3} + 2\sqrt{y} & = & -1 \end{array} \right.\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-78f66d69e19938ccf8567677fc469a22_l3.png)
- The polynomial
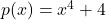 can be factored into the product linear and irreducible quadratic factors. In this exercise, we present a method for obtaining that factorization.
can be factored into the product linear and irreducible quadratic factors. In this exercise, we present a method for obtaining that factorization.
- Show that
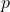 has no real zeros.
has no real zeros. - Because
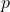 has no real zeros, its factorization must be of the form
has no real zeros, its factorization must be of the form 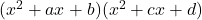 where each factor is an irreducible quadratic. Expand this quantity and gather like terms together.
where each factor is an irreducible quadratic. Expand this quantity and gather like terms together. - Create and solve the system of nonlinear equations which results from equating the coefficients of the expansion found above with those of
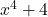 . You should get four equations in the four unknowns
. You should get four equations in the four unknowns  ,
, 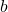 ,
,  and
and 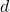 . Write
. Write 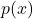 in factored form.
in factored form.
- Show that
Section 6.2 Exercise Answers can be found in the Appendix … Coming soon

