7.1 Degree and Radian Measure of Angles
This section serves as a review of the concept of `angle’ and the use of the degree and radian systems to measure angles.
7.1.1 Degree Measure
Recall that a ray is usually described as a `half-line’ and can be thought of as a line segment in which one of the two endpoints is pushed off infinitely distant from the other, as pictured below. The point from which the ray originates is called the initial point of the ray.
When two rays share a common initial point they form an angle and the common initial point is called the vertex of the angle. Two examples of what are commonly thought of as angles are

However, the two figures below also depict angles – albeit these are, in some sense, extreme cases. In the first case, the two rays are directly opposite each other forming what is known as a straight angle; in the second, the rays are identical so the `angle’ is indistinguishable from the ray itself.

The measure of an angle is a number which indicates the amount of rotation that separates the rays of the angle. There is one immediate problem with this, as pictured below.

Which amount of rotation are we attempting to quantify? What we have just discovered is that we have at least two angles described by this diagram.[1] Clearly these two angles have different measures because one appears to represent a larger rotation than the other, so we must label them differently. In this book, we use lower case Greek letters such as ![]() (alpha),
(alpha), ![]() (beta),
(beta), ![]() (gamma) and
(gamma) and ![]() (theta) to label angles. So, for instance, we have
(theta) to label angles. So, for instance, we have
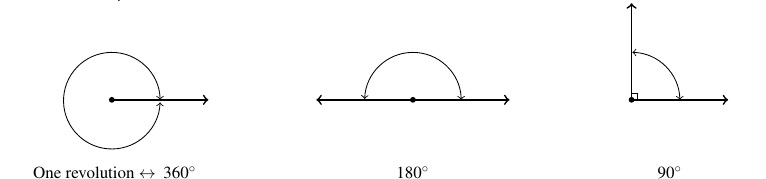
One system to measure angles is degree measure. Quantities measured in degrees are denoted by the symbol `![]() .’ One complete revolution as shown below is
.’ One complete revolution as shown below is ![]() , and parts of a revolution are measured proportionately.[2] Thus half of a revolution (a straight angle) measures
, and parts of a revolution are measured proportionately.[2] Thus half of a revolution (a straight angle) measures ![]() , a quarter of a revolution (a right angle) measures
, a quarter of a revolution (a right angle) measures ![]() and so on.
and so on.
Note that in the above figure, we have used the small square ![]() to denote a right angle, as is commonplace in Geometry. Recall that if an angle measures strictly between
to denote a right angle, as is commonplace in Geometry. Recall that if an angle measures strictly between ![]() and
and ![]() it is called an acute angle and if it measures strictly between
it is called an acute angle and if it measures strictly between ![]() and
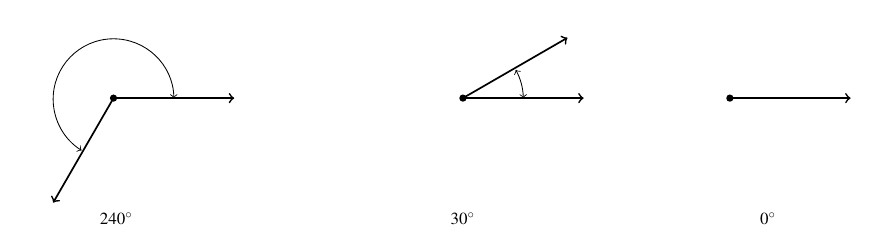
and ![]() it is called an obtuse angle. It is important to note that, theoretically, we can know the measure of any angle as long as we know the proportion it represents of an entire revolution.[3] For instance, the measure of an angle which represents a rotation of
it is called an obtuse angle. It is important to note that, theoretically, we can know the measure of any angle as long as we know the proportion it represents of an entire revolution.[3] For instance, the measure of an angle which represents a rotation of ![]() of a revolution would measure
of a revolution would measure ![]() , the measure of an angle which constitutes only
, the measure of an angle which constitutes only ![]() of a revolution measures
of a revolution measures ![]() and an angle which indicates no rotation at all is measured as
and an angle which indicates no rotation at all is measured as ![]() .
.
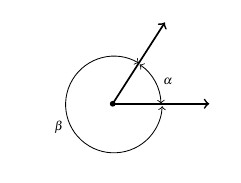
Recall that two acute angles are called complementary angles if their measures add to ![]() . Two angles, either a pair of right angles or one acute angle and one obtuse angle, are called supplementary angles if their measures add to
. Two angles, either a pair of right angles or one acute angle and one obtuse angle, are called supplementary angles if their measures add to ![]() . In the diagram below, the angles
. In the diagram below, the angles ![]() and
and ![]() are supplementary angles while the pair
are supplementary angles while the pair ![]() and
and ![]() are complementary angles.
are complementary angles.
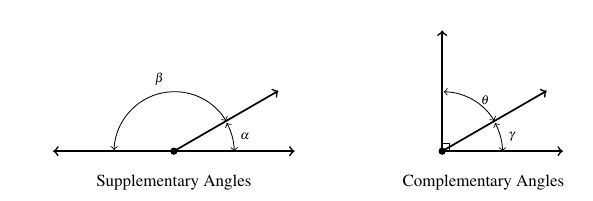
In practice, the distinction between the angle itself and its measure is blurred so that the sentence `![]() is an angle measuring
is an angle measuring ![]() ‘ is often abbreviated as `
‘ is often abbreviated as `![]() .’ It is now time for an example.
.’ It is now time for an example.
Example 7.1.1
Example 7.1.1.1
Let ![]() and
and ![]() .
.
Sketch ![]() and
and ![]() .
.
Solution:
Sketch ![]() and
and ![]() .
.
To sketch ![]() , we first note that
, we first note that ![]() . Dividing this range in half, we get
. Dividing this range in half, we get ![]() , and once more, we have
, and once more, we have ![]() . This gives us a pretty good estimate for
. This gives us a pretty good estimate for ![]() , as shown below.
, as shown below.
Proceeding similarly for ![]() , we find
, we find ![]() , then
, then ![]() ,
, ![]() , and lastly,
, and lastly, ![]() .
.
Example 7.1.1.2
Let ![]() and
and ![]() .
.
Compute a supplementary angle for ![]() .
.
Solution:
Compute a supplementary angle for ![]() .
.
To find a supplementary angle for ![]() , we seek an angle
, we seek an angle ![]() so that
so that ![]() .
.
We get ![]() .
.
Example 7.1.1.3
Let ![]() and
and ![]() .
.
Compute a complementary angle for ![]() .
.
Solution:
Compute a complementary angle for ![]() .
.
To find a complementary angle for ![]() , we seek an angle
, we seek an angle ![]() so that
so that ![]() .
.
We get ![]() .
.
Up to this point, we have discussed only angles which measure between ![]() and
and ![]() , inclusive. Ultimately, we want to use the arsenal of Algebra which we have stockpiled in Chapters 1 through 6 to not only solve geometric problems involving angles, but also to extend their applicability to other real-world phenomena. A first step in this direction is to extend our notion of `angle’ from merely measuring an extent of rotation to quantities which indicate an amount of rotation along with a direction. To that end, we introduce the concept of an oriented angle. As its name suggests, in an oriented angle, the direction of the rotation is important. We imagine the angle being swept out starting from an initial side and ending at a terminal side, as shown below. When the rotation is counter-clockwise from initial side to terminal side, we say that the angle is positive; when the rotation is clockwise, we say that the angle is negative.
, inclusive. Ultimately, we want to use the arsenal of Algebra which we have stockpiled in Chapters 1 through 6 to not only solve geometric problems involving angles, but also to extend their applicability to other real-world phenomena. A first step in this direction is to extend our notion of `angle’ from merely measuring an extent of rotation to quantities which indicate an amount of rotation along with a direction. To that end, we introduce the concept of an oriented angle. As its name suggests, in an oriented angle, the direction of the rotation is important. We imagine the angle being swept out starting from an initial side and ending at a terminal side, as shown below. When the rotation is counter-clockwise from initial side to terminal side, we say that the angle is positive; when the rotation is clockwise, we say that the angle is negative.
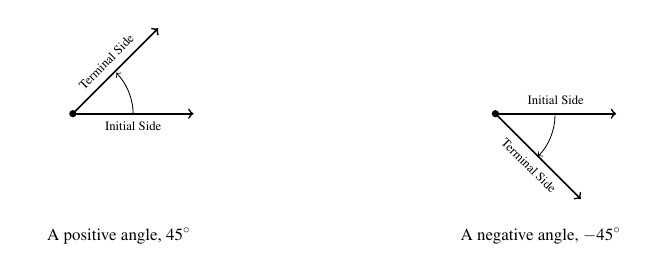
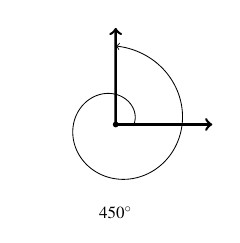
At this point, we also extend our allowable rotations to include angles which encompass more than one revolution. For example, to sketch an angle with measure ![]() we start with an initial side, rotate counter-clockwise one complete revolution (to take care of the `first’
we start with an initial side, rotate counter-clockwise one complete revolution (to take care of the `first’ ![]() ) then continue with an additional
) then continue with an additional ![]() counter-clockwise rotation, as seen below.
counter-clockwise rotation, as seen below.
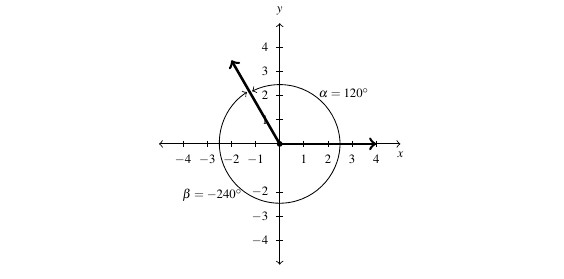
To further connect angles with the Algebra which has come before, we shall often overlay an angle diagram on the coordinate plane. An angle is said to be in standard position if its vertex is the origin and its initial side coincides with the positive horizontal (usually labeled as the ![]() -) axis. Angles in standard position are classified according to where their terminal side lies. For instance, an angle in standard position whose terminal side lies in Quadrant I is called a `Quadrant I angle’. If the terminal side of an angle lies on one of the coordinate axes, it is called a quadrantal angle. Two angles in standard position are called coterminal if they share the same terminal side.[4] In the figure below,
-) axis. Angles in standard position are classified according to where their terminal side lies. For instance, an angle in standard position whose terminal side lies in Quadrant I is called a `Quadrant I angle’. If the terminal side of an angle lies on one of the coordinate axes, it is called a quadrantal angle. Two angles in standard position are called coterminal if they share the same terminal side.[4] In the figure below, ![]() and
and ![]() are two coterminal Quadrant II angles drawn in standard position. Note that
are two coterminal Quadrant II angles drawn in standard position. Note that ![]() , or equivalently,
, or equivalently, ![]() . We leave it as an exercise to the reader to verify that coterminal angles always differ by a multiple of
. We leave it as an exercise to the reader to verify that coterminal angles always differ by a multiple of ![]() .[5] More precisely, if
.[5] More precisely, if ![]() and
and ![]() are coterminal angles, then
are coterminal angles, then ![]() where
where ![]() is an integer.[6]
is an integer.[6]
Example 7.1.2
Example 7.1.2.1
Graph each of the (oriented) angles below in standard position and classify them according to where their terminal side lies. Determine three coterminal angles, at least one of which is positive and one of which is negative.
![]()
Solution:
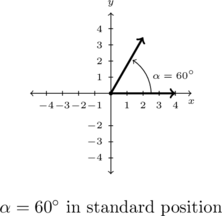
Graph ![]() in standard position.
in standard position.
To graph ![]() , we draw an angle with its initial side on the positive
, we draw an angle with its initial side on the positive ![]() -axis and rotate counter-clockwise
-axis and rotate counter-clockwise ![]() of a revolution. We see that
of a revolution. We see that ![]() is a Quadrant I angle.
is a Quadrant I angle.
To find angles which are coterminal, we look for angles ![]() of the form
of the form ![]() , for some integer
, for some integer ![]() .
.
When ![]() , we get
, we get ![]() .
.
Substituting ![]() gives
gives ![]() .
.
Finally, if we let ![]() , we get
, we get ![]() .
.
Example 7.1.2.2
Graph each of the (oriented) angles below in standard position and classify them according to where their terminal side lies. Determine three coterminal angles, at least one of which is positive and one of which is negative.
![]()
Solution:
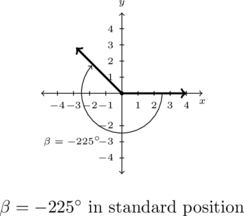
Graph ![]() in standard position.
in standard position.
As a result of ![]() being negative, we start at the positive
being negative, we start at the positive ![]() -axis and rotate clockwise
-axis and rotate clockwise ![]() of a revolution. We see that
of a revolution. We see that ![]() is a Quadrant II angle.
is a Quadrant II angle.
To find coterminal angles, we proceed as before and compute ![]() for integer values of
for integer values of ![]() .
.
We find ![]() ,
, ![]() and
and ![]() are all coterminal with
are all coterminal with ![]() , when
, when ![]() , and 2 respectively.
, and 2 respectively.
Example 7.1.2.3
Graph each of the (oriented) angles below in standard position and classify them according to where their terminal side lies. Determine three coterminal angles, at least one of which is positive and one of which is negative.
![]()
Solution:
Graph ![]() in standard position.
in standard position.
As ![]() is positive, we rotate counter-clockwise from the positive
is positive, we rotate counter-clockwise from the positive ![]() -axis. One full revolution accounts for
-axis. One full revolution accounts for ![]() , with
, with ![]() , or
, or ![]() of a revolution remaining. The terminal side of
of a revolution remaining. The terminal side of ![]() lies on the negative
lies on the negative ![]() -axis, so
-axis, so ![]() is a quadrantal angle.
is a quadrantal angle.
All angles coterminal with ![]() are of the form
are of the form ![]() , where
, where ![]() is an integer.
is an integer.
Working through the arithmetic as before, we find three such angles: ![]() ,
, ![]() and
and ![]() .
.
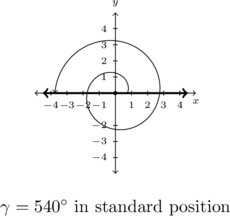
Example 7.1.2.4
Graph each of the (oriented) angles below in standard position and classify them according to where their terminal side lies. Determine three coterminal angles, at least one of which is positive and one of which is negative.
![]()
Solution:
Graph ![]() in standard position.
in standard position.
The Greek letter ![]() is pronounced `fee’ or `fie’ and because
is pronounced `fee’ or `fie’ and because ![]() is negative, we begin our rotation clockwise from the positive
is negative, we begin our rotation clockwise from the positive ![]() -axis. Two full revolutions account for
-axis. Two full revolutions account for ![]() , with just
, with just ![]() or
or ![]() of a revolution to go. We find that
of a revolution to go. We find that ![]() is a Quadrant IV angle.
is a Quadrant IV angle.
To find coterminal angles, we compute ![]() for a few integers
for a few integers ![]() and obtain
and obtain ![]() ,
, ![]() and
and ![]() .
.
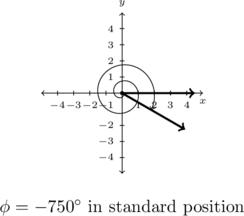
7.1.2 Radian Measure
While degrees are the unit of choice for many applications of trigonometry, we introduce here the concept of the radian measure of an angle. As we will see, this concept naturally ties angles to real numbers. While the concept may seem foreign at first, we assure the reader that the utility of radian measure in modeling real-world phenomena is well worth the effort. We begin our development with a definition from Geometry.
Definition 7.1
The real number ![]() is defined to be the ratio of a circle’s circumference to its diameter. In symbols, given a circle of circumference
is defined to be the ratio of a circle’s circumference to its diameter. In symbols, given a circle of circumference ![]() and diameter
and diameter ![]() ,
,
![]()
While Definition 7.1 is quite possibly the `standard’ definition of ![]() , the authors would be remiss if we didn’t mention that buried in this definition is actually a theorem. As the reader is probably aware, the number
, the authors would be remiss if we didn’t mention that buried in this definition is actually a theorem. As the reader is probably aware, the number ![]() is a mathematical constant – that is, it doesn’t matter which circle is selected, the ratio of its circumference to its diameter will have the same value as any other circle. While this is indeed true, it is far from obvious and leads to a counter intuitive scenario which is explored in the Exercises. Because the diameter of a circle is twice its radius, we can quickly rearrange the equation in Definition 7.1 to get a formula more useful for our purposes, namely:
is a mathematical constant – that is, it doesn’t matter which circle is selected, the ratio of its circumference to its diameter will have the same value as any other circle. While this is indeed true, it is far from obvious and leads to a counter intuitive scenario which is explored in the Exercises. Because the diameter of a circle is twice its radius, we can quickly rearrange the equation in Definition 7.1 to get a formula more useful for our purposes, namely: ![]() . Hence, for any circle, the ratio of its circumference to its radius is
. Hence, for any circle, the ratio of its circumference to its radius is ![]() .
.
Suppose we take a portion of the circle, and we compare some arc measuring ![]() units in length to the radius. Let
units in length to the radius. Let ![]() be the central angle subtended by this arc, that is, an angle whose vertex is the center of the circle and whose determining rays pass through the endpoints of the arc. Using proportionality (similarity) arguments, it stands to reason that the ratio
be the central angle subtended by this arc, that is, an angle whose vertex is the center of the circle and whose determining rays pass through the endpoints of the arc. Using proportionality (similarity) arguments, it stands to reason that the ratio ![]() should also be a constant among all circles. It is this ratio,
should also be a constant among all circles. It is this ratio, ![]() , which defines the radian measure of an angle.
, which defines the radian measure of an angle.
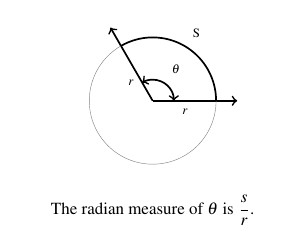
To get a better feel for radian measure, we note that an angle with radian measure ![]() means the corresponding arc length
means the corresponding arc length ![]() equals the radius of the circle
equals the radius of the circle ![]() , that is,
, that is, ![]() . When the radian measure is
. When the radian measure is ![]() , we have
, we have ![]() ; when the radian measure is
; when the radian measure is ![]() ,
, ![]() , and so forth. Thus the radian measure of an angle
, and so forth. Thus the radian measure of an angle ![]() tells us how many `radius lengths’ we need to sweep out along the circle to subtend the angle
tells us how many `radius lengths’ we need to sweep out along the circle to subtend the angle ![]() .
.
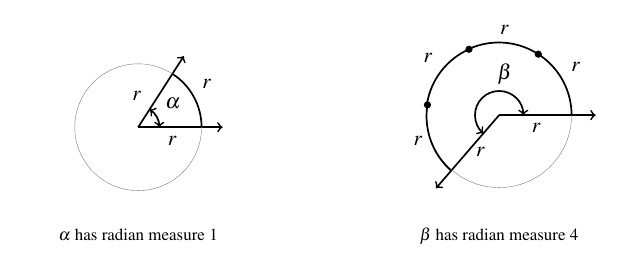
One revolution sweeps out the circumference ![]() , so one revolution has radian measure
, so one revolution has radian measure ![]() . From this we can find the radian measure of other central angles using proportions, just like we did with degrees. For instance, half of a revolution has radian measure
. From this we can find the radian measure of other central angles using proportions, just like we did with degrees. For instance, half of a revolution has radian measure ![]() , a quarter revolution has radian measure
, a quarter revolution has radian measure ![]() , and so forth. Note that, by definition, the radian measure of an angle is a length divided by another length so that these measurements are actually dimensionless and are considered `pure’ numbers. For this reason, we do not use any symbols to denote radian measure, but we use the word `radians’ to denote these dimensionless units as needed. For instance, we say one revolution measures `
, and so forth. Note that, by definition, the radian measure of an angle is a length divided by another length so that these measurements are actually dimensionless and are considered `pure’ numbers. For this reason, we do not use any symbols to denote radian measure, but we use the word `radians’ to denote these dimensionless units as needed. For instance, we say one revolution measures `![]() radians,’ half of a revolution measures `
radians,’ half of a revolution measures `![]() radians,’ and so forth.
radians,’ and so forth.
Arc Length
Given ![]() is a central angle of a circle with radius
is a central angle of a circle with radius ![]() , the length of the subtended arc of length
, the length of the subtended arc of length ![]() is
is ![]() , where
, where ![]() is in radians.
is in radians.
As with degree measure, the distinction between the angle itself and its measure is often blurred in practice, so when we write `![]() ‘, we mean
‘, we mean ![]() is an angle which measures
is an angle which measures ![]() radians.[7] We extend radian measure to oriented angles, just as we did with degrees beforehand, so that a positive measure indicates counter-clockwise rotation and a negative measure indicates clockwise rotation.[8] Much like before, two positive angles
radians.[7] We extend radian measure to oriented angles, just as we did with degrees beforehand, so that a positive measure indicates counter-clockwise rotation and a negative measure indicates clockwise rotation.[8] Much like before, two positive angles ![]() and
and ![]() are supplementary if
are supplementary if ![]() and complementary if
and complementary if ![]() . Finally, we leave it to the reader to show that when using radian measure, two angles
. Finally, we leave it to the reader to show that when using radian measure, two angles ![]() and
and ![]() are coterminal if and only if
are coterminal if and only if ![]() for some integer
for some integer ![]() .
.
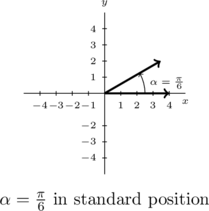
Example 7.1.3
Example 7.1.3.1
Graph each of the (oriented) angles below in standard position and classify them according to where their terminal side lies. Find three coterminal angles, at least one of which is positive and one of which is negative.
![]()
Solution:
Graph and classify ![]() .
.
The angle ![]() is positive, so we draw an angle with its initial side on the positive
is positive, so we draw an angle with its initial side on the positive ![]() -axis and rotate counter-clockwise
-axis and rotate counter-clockwise ![]() of a revolution. Thus
of a revolution. Thus ![]() is a Quadrant I angle.
is a Quadrant I angle.
Coterminal angles ![]() are of the form
are of the form ![]() , for some integer
, for some integer ![]() .
.
To make the arithmetic a bit easier, we note that ![]() , thus when
, thus when ![]() , we get
, we get ![]() .
.
Substituting ![]() gives
gives ![]() and when we let
and when we let ![]() , we get
, we get ![]() .
.
Example 7.1.3.2
Graph each of the (oriented) angles below in standard position and classify them according to where their terminal side lies. Find three coterminal angles, at least one of which is positive and one of which is negative.
![]()
Solution:
Graph and classify ![]() .
.
As ![]() is negative, we start at the positive
is negative, we start at the positive ![]() -axis and rotate clockwise
-axis and rotate clockwise ![]() of a revolution. We find
of a revolution. We find ![]() to be a Quadrant II angle.
to be a Quadrant II angle.
To find coterminal angles, we proceed as before using ![]() , and compute
, and compute ![]() for integer values of
for integer values of ![]() .
.
We obtain ![]() ,
, ![]() and
and ![]() as coterminal angles.
as coterminal angles.
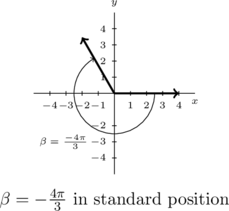
Example 7.1.3.3
Graph each of the (oriented) angles below in standard position and classify them according to where their terminal side lies. Find three coterminal angles, at least one of which is positive and one of which is negative.
![]()
Solution:
Graph and classify ![]() .
.
As ![]() is positive, we rotate counter-clockwise from the positive
is positive, we rotate counter-clockwise from the positive ![]() -axis. One full revolution accounts for
-axis. One full revolution accounts for ![]() of the radian measure with
of the radian measure with ![]() or
or ![]() of a revolution remaining. We have
of a revolution remaining. We have ![]() as a Quadrant I angle.
as a Quadrant I angle.
All angles coterminal with ![]() are of the form
are of the form ![]() , where
, where ![]() is an integer.
is an integer.
Working through the arithmetic for ![]() , we find:
, we find: ![]() ,
, ![]() and
and ![]() , respectively.
, respectively.
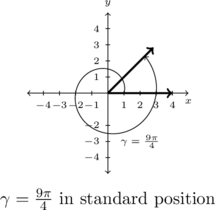
Example 7.1.3.4
Graph each of the (oriented) angles below in standard position and classify them according to where their terminal side lies. Find three coterminal angles, at least one of which is positive and one of which is negative.
![]()
Solution:
Graph and classify ![]() .
.
To graph ![]() , we begin our rotation clockwise from the positive
, we begin our rotation clockwise from the positive ![]() -axis. As
-axis. As ![]() , after one full revolution clockwise, we have
, after one full revolution clockwise, we have ![]() or
or ![]() of a revolution remaining. The terminal side of
of a revolution remaining. The terminal side of ![]() lies on the negative
lies on the negative ![]() -axis, thus
-axis, thus ![]() is a quadrantal angle.
is a quadrantal angle.
To find coterminal angles, we compute ![]() for a few integers
for a few integers ![]() and obtain
and obtain ![]() ,
, ![]() and
and ![]() .
.
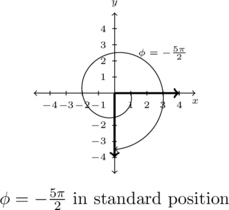
It is worth mentioning that we could have plotted the angles in Example 7.1.3 by first converting them to degree measure and following the procedure set forth in Example 7.1.2. While converting back and forth from degrees and radians is certainly a good skill to have, it is best that you learn to `think in radians’ as well as you can `think in degrees’. The authors would, however, be derelict in our duties if we ignored the basic conversion between these systems altogether. As one revolution counter-clockwise measures ![]() and the same angle measures
and the same angle measures ![]() radians, we can use the proportion
radians, we can use the proportion ![]() , or its reduced equivalent,
, or its reduced equivalent, ![]() , as the conversion factor between the two systems. For example, to convert
, as the conversion factor between the two systems. For example, to convert ![]() to radians we find
to radians we find ![]() , or simply
, or simply ![]() . To convert from radian measure back to degrees, we multiply by the ratio
. To convert from radian measure back to degrees, we multiply by the ratio ![]() . For example,
. For example, ![]() is equal to
is equal to ![]() .[9] Hence, an angle which measures
.[9] Hence, an angle which measures ![]() in radian measure is equal to
in radian measure is equal to ![]() . To summarize:
. To summarize:
Equation 7.1 Degree – Radian Conversion
- To convert degree measure to radian measure, multiply by
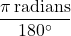
- To convert radian measure to degree measure, multiply by
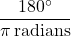
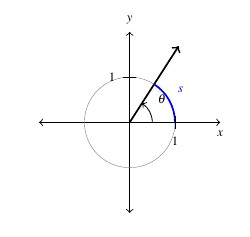
In light of Example 7.1.3 and Equation 7.1.2, the reader may well wonder what the allure of radian measure is. The numbers involved are, admittedly, much more complicated than degree measure. The answer lies in how easily angles in radian measure can be identified with real numbers. Consider the Unit Circle, ![]() , the angle
, the angle ![]() in standard position and the corresponding arc measuring
in standard position and the corresponding arc measuring ![]() units in length. By definition, and the fact that the Unit Circle has radius 1, the radian measure of
units in length. By definition, and the fact that the Unit Circle has radius 1, the radian measure of ![]() is
is ![]() so that, once again blurring the distinction between an angle and its measure, we have
so that, once again blurring the distinction between an angle and its measure, we have ![]() . In order to identify real numbers with oriented angles, we essentially `wrap’ \index{wrapping function} the real number line around the Unit Circle and associating to each real number
. In order to identify real numbers with oriented angles, we essentially `wrap’ \index{wrapping function} the real number line around the Unit Circle and associating to each real number ![]() an oriented arc on the Unit Circle with initial point
an oriented arc on the Unit Circle with initial point ![]() .
.
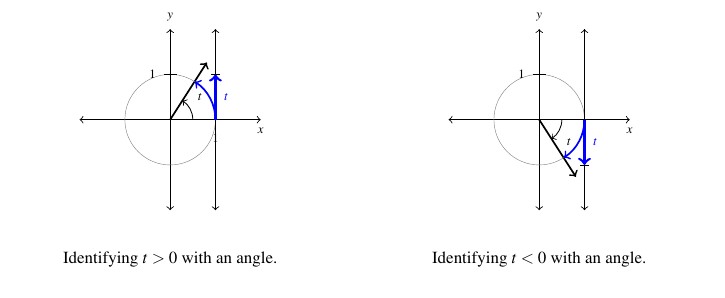
Viewing the vertical line ![]() as another real number line demarcated like the
as another real number line demarcated like the ![]() -axis, given a real number
-axis, given a real number ![]() , we `wrap’ the (vertical) interval
, we `wrap’ the (vertical) interval ![]() around the Unit Circle in a counter-clockwise fashion. The resulting arc has a length of
around the Unit Circle in a counter-clockwise fashion. The resulting arc has a length of ![]() units and therefore the corresponding angle has radian measure equal to
units and therefore the corresponding angle has radian measure equal to ![]() . If
. If ![]() , we wrap the interval
, we wrap the interval ![]() clockwise around the Unit Circle. We have defined clockwise rotation as having negative radian measure, therefore the angle determined by this arc has radian measure equal to
clockwise around the Unit Circle. We have defined clockwise rotation as having negative radian measure, therefore the angle determined by this arc has radian measure equal to ![]() . If
. If ![]() , we are at the point
, we are at the point ![]() on the
on the ![]() -axis which corresponds to an angle with radian measure
-axis which corresponds to an angle with radian measure ![]() . In this way, we identify each real number
. In this way, we identify each real number ![]() with the corresponding angle with radian measure
with the corresponding angle with radian measure ![]() .
.
Example 7.1.4
Example 7.1.4.1
Sketch the oriented arc on the Unit Circle corresponding to each of the following real numbers.
![]()
Solution:
Sketch the oriented arc on the Unit Circle corresponding to ![]() .
.
The arc associated with ![]() is the arc on the Unit Circle which subtends the angle
is the arc on the Unit Circle which subtends the angle ![]() in radian measure. As
in radian measure. As ![]() is
is ![]() of a revolution, we have an arc which begins at the point
of a revolution, we have an arc which begins at the point ![]() proceeds counter-clockwise up to midway through Quadrant II.
proceeds counter-clockwise up to midway through Quadrant II.

Example 7.1.4.2
Sketch the oriented arc on the Unit Circle corresponding to each of the following real numbers.
![]()
Solution:
Sketch the oriented arc on the Unit Circle corresponding to ![]() .
.
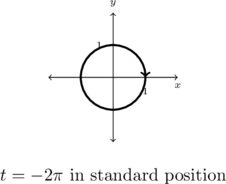
One revolution is ![]() radians and
radians and ![]() is negative, so we graph the arc which begins at
is negative, so we graph the arc which begins at ![]() and proceeds clockwise for one full revolution.
and proceeds clockwise for one full revolution.
Example 7.1.4.3
Sketch the oriented arc on the Unit Circle corresponding to each of the following real numbers.
![]()
Solution:
Sketch the oriented arc on the Unit Circle corresponding to ![]() .
.
Like ![]() ,
, ![]() is negative, so we begin our arc at
is negative, so we begin our arc at ![]() and proceed clockwise around the unit circle. Because
and proceed clockwise around the unit circle. Because ![]() and
and ![]() , we find that rotating
, we find that rotating ![]() radians clockwise from the point
radians clockwise from the point ![]() lands us in Quadrant III. To more accurately place the endpoint, we proceed by successively halving the angle measure until we find
lands us in Quadrant III. To more accurately place the endpoint, we proceed by successively halving the angle measure until we find ![]() which tells us our arc extends just a bit beyond the quarter mark into Quadrant III.
which tells us our arc extends just a bit beyond the quarter mark into Quadrant III.

Example 7.1.4.4
Sketch the oriented arc on the Unit Circle corresponding to each of the following real numbers.
![]()
Solution:
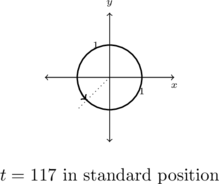
Sketch the oriented arc on the Unit Circle corresponding to ![]() .
.
Because ![]() is positive, the arc corresponding to
is positive, the arc corresponding to ![]() begins at
begins at ![]() and proceeds counter-clockwise. As
and proceeds counter-clockwise. As ![]() is much greater than
is much greater than ![]() , we wrap around the Unit Circle several times before finally reaching our endpoint. We approximate
, we wrap around the Unit Circle several times before finally reaching our endpoint. We approximate ![]() as
as ![]() which tells us we complete
which tells us we complete ![]() revolutions counter-clockwise with
revolutions counter-clockwise with ![]() , or just shy of
, or just shy of ![]() of a revolution to spare. In other words, the terminal side of the angle which measures
of a revolution to spare. In other words, the terminal side of the angle which measures ![]() radians in standard position is just short of being midway through Quadrant III.
radians in standard position is just short of being midway through Quadrant III.
7.1.3 Applications of Radian Measure: Circular Motion
Now that we have paired angles with real numbers via radian measure, a whole world of applications awaits us. Our first excursion into this realm comes by way of circular motion. Suppose an object is moving as pictured below along a circular path of radius ![]() from the point
from the point ![]() to the point
to the point ![]() in an amount of time
in an amount of time ![]() .
.
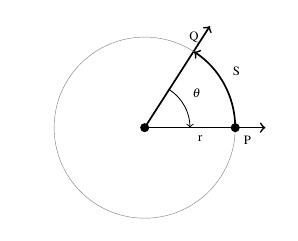
Here ![]() represents a displacement, so that
represents a displacement, so that ![]() means the object is traveling in a counter-clockwise direction and
means the object is traveling in a counter-clockwise direction and ![]() indicates movement in a clockwise direction. Note that with this convention the formula we used to define radian measure, namely
indicates movement in a clockwise direction. Note that with this convention the formula we used to define radian measure, namely ![]() , still holds as a negative value of
, still holds as a negative value of ![]() incurred from a clockwise displacement matches the negative we assign to
incurred from a clockwise displacement matches the negative we assign to ![]() for a clockwise rotation. In Physics, the average velocity of the object, denoted
for a clockwise rotation. In Physics, the average velocity of the object, denoted ![]() and read as `
and read as `![]() -bar’, is defined as the average rate of change of the position of the object with respect to time.[10] As a result, we have
-bar’, is defined as the average rate of change of the position of the object with respect to time.[10] As a result, we have ![]() . The quantity
. The quantity ![]() has units of
has units of ![]() and conveys two ideas: the direction in which the object is moving and how fast the position of the object is changing. The contribution of direction in the quantity
and conveys two ideas: the direction in which the object is moving and how fast the position of the object is changing. The contribution of direction in the quantity ![]() is either to make it positive (in the case of counter-clockwise motion) or negative (in the case of clockwise motion), so that the quantity
is either to make it positive (in the case of counter-clockwise motion) or negative (in the case of clockwise motion), so that the quantity ![]() quantifies how fast the object is moving – it is the speed of the object. Measuring
quantifies how fast the object is moving – it is the speed of the object. Measuring ![]() in radians we have
in radians we have ![]() thus
thus ![]() and
and
![]()
The quantity ![]() is called the average angular velocity of the object. It is denoted by
is called the average angular velocity of the object. It is denoted by ![]() and is read `omega-bar’. The quantity
and is read `omega-bar’. The quantity ![]() is the average rate of change of the angle
is the average rate of change of the angle ![]() with respect to time and thus has units
with respect to time and thus has units ![]() . If
. If ![]() is constant throughout the duration of the motion, then it can be shown[11] that the average velocities involved, namely
is constant throughout the duration of the motion, then it can be shown[11] that the average velocities involved, namely ![]() and
and ![]() , are the same as their instantaneous counterparts,
, are the same as their instantaneous counterparts, ![]() and
and ![]() , respectively. In this case,
, respectively. In this case, ![]() is simply called the `velocity’ of the object and
is simply called the `velocity’ of the object and ![]() is called the `angular velocity.’[12]
is called the `angular velocity.’[12]
If the path of the object were `uncurled’ from a circle to form a line segment, then the velocity of the object on that line segment would be the same as the velocity on the circle. For this reason, the quantity ![]() is often called the linear velocity of the object in order to distinguish it from the angular velocity,
is often called the linear velocity of the object in order to distinguish it from the angular velocity, ![]() . Putting together the ideas of the previous paragraph, we get the following.
. Putting together the ideas of the previous paragraph, we get the following.
Equation 7.2 Velocity of Circular Motion
For an object moving on a circular path of radius ![]() with constant angular velocity
with constant angular velocity ![]() , the (linear) velocity of the object is given by
, the (linear) velocity of the object is given by ![]() .
.
We need to talk about units here. The units of ![]() are
are ![]() , the units of
, the units of ![]() are length only, and the units of
are length only, and the units of ![]() are
are ![]() . Thus the left hand side of the equation
. Thus the left hand side of the equation ![]() has units
has units ![]() , whereas the right hand side has units
, whereas the right hand side has units ![]() . The supposed contradiction in units is resolved by remembering that radians are a dimensionless quantity and angles in radian measure are identified with real numbers so that the units
. The supposed contradiction in units is resolved by remembering that radians are a dimensionless quantity and angles in radian measure are identified with real numbers so that the units ![]() reduce to the units
reduce to the units ![]() . We are long overdue for an example.
. We are long overdue for an example.
Example 7.1.5
Example 7.1.5
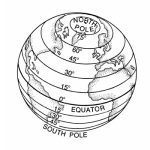
Assuming that the surface of the Earth is a sphere, any point on the Earth can be thought of as an object traveling on a circle (this is the parallel of latitude of the point) as seen in the figure below.[13] It takes the Earth (approximately) 24 hours to rotate, so the object takes 24 hours to complete one revolution along this circle. Lakeland Community College is at ![]() north latitude, and it can be shown[14] that the radius of the earth at this Latitude is approximately
north latitude, and it can be shown[14] that the radius of the earth at this Latitude is approximately ![]() miles. Find the linear velocity, in miles per hour, of Lakeland Community College as the world turns.
miles. Find the linear velocity, in miles per hour, of Lakeland Community College as the world turns.
Solution:
To use the formula ![]() , we first need to compute the angular velocity
, we first need to compute the angular velocity ![]() . The earth makes one revolution in 24 hours, and one revolution is
. The earth makes one revolution in 24 hours, and one revolution is ![]() radians, so
radians, so
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \omega &=& \frac{2 \pi \, \text{radians}}{24 \, \text{hours}} \\[6pt] &=& \frac{\pi}{12 \, \text{hours}} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-967510e7567125d584d534464c2b1cfe_l3.png)
Note that once again, we are identifying angles in radian measure as real numbers so we can drop the `radian’ units as they are dimensionless. Also note that for simplicity’s sake, we assume that we are viewing the rotation of the earth as counter-clockwise so ![]() . Hence, the linear velocity is
. Hence, the linear velocity is
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} v &=& 2960 \, \text{miles} \cdot \frac{\pi}{12 \, \text{hours}} \\[6pt] &\approx & 775 \, \frac{\text{miles}}{\text{hour}} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4b21fbd8e9b07df5644f4a51af33163f_l3.png)
It is worth noting that the quantity ![]() in Example 7.1.5 is called the ordinary frequency of the motion and is usually denoted by the variable
in Example 7.1.5 is called the ordinary frequency of the motion and is usually denoted by the variable ![]() . The ordinary frequency is a measure of how often an object makes a complete cycle of the motion. The fact that
. The ordinary frequency is a measure of how often an object makes a complete cycle of the motion. The fact that ![]() suggests that
suggests that ![]() is also a frequency. Indeed, it is called the angular frequency of the motion. On a related note, the quantity
is also a frequency. Indeed, it is called the angular frequency of the motion. On a related note, the quantity ![]() is called the period of the motion and is the amount of time it takes for the object to complete one cycle of the motion. In the scenario of Example 7.1.5, the period of the motion is 24 hours, or one day.
is called the period of the motion and is the amount of time it takes for the object to complete one cycle of the motion. In the scenario of Example 7.1.5, the period of the motion is 24 hours, or one day.
The concepts of frequency and period help frame the equation ![]() in a new light. That is, if
in a new light. That is, if ![]() is fixed, points which are farther from the center of rotation need to travel faster to maintain the same angular frequency because they have farther to travel to make one revolution in one period’s time. The distance of the object to the center of rotation is the radius of the circle,
is fixed, points which are farther from the center of rotation need to travel faster to maintain the same angular frequency because they have farther to travel to make one revolution in one period’s time. The distance of the object to the center of rotation is the radius of the circle, ![]() , and is the `magnification factor’ which relates
, and is the `magnification factor’ which relates ![]() and
and ![]() . We will have more to say about frequencies and periods in Section 7.3. While we have exhaustively discussed velocities associated with circular motion, we have yet to discuss a more natural question: if an object is moving on a circular path of radius
. We will have more to say about frequencies and periods in Section 7.3. While we have exhaustively discussed velocities associated with circular motion, we have yet to discuss a more natural question: if an object is moving on a circular path of radius ![]() with a fixed angular velocity (frequency)
with a fixed angular velocity (frequency) ![]() , what is the position of the object at time
, what is the position of the object at time ![]() ? The answer to this question is the very heart of Trigonometry and is answered in the next section.
? The answer to this question is the very heart of Trigonometry and is answered in the next section.
7.1.4 Section Exercises
In Exercises 1 – 12, graph the oriented angle in standard position. Classify each angle according to where its terminal side lies and then give two coterminal angles, one of which is positive and the other negative.
In Exercises 13 – 28, graph the oriented angle in standard position. Classify each angle according to where its terminal side lies and then give two coterminal angles, one of which is positive and the other negative.
In Exercises 29 – 36, convert the angle from degree measure into radian measure, giving the exact value in terms of ![]() .
.
In Exercises 37 – 44, convert the angle from radian measure into degree measure.
In Exercises 45 – 49, sketch the oriented arc on the Unit Circle which corresponds to the given real number.
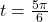
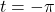
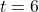
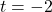
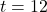
- A yo-yo which is 2.25 inches in diameter spins at a rate of 4500 revolutions per minute. How fast is the edge of the yo-yo spinning in miles per hour? Leave your answer in exact form.
- How many revolutions per minute would the yo-yo in Exercise 50 have to complete if the edge of the yo-yo is to be spinning at a rate of 42 miles per hour? Leave your answer in exact form.
- In the yo-yo trick `Around the World,’ the performer throws the yo-yo so it sweeps out a vertical circle whose radius is the yo-yo string. If the yo-yo string is 28 inches long and the yo-yo takes 3 seconds to complete one revolution of the circle, compute the speed of the yo-yo in miles per hour. Leave your answer in exact form.
- A computer hard drive contains a circular disk with diameter 2.5 inches and spins at a rate of 7200 revolutions per minute. Find the linear speed of a point on the edge of the disk in miles per hour.
- A rock got stuck in the tread of my tire and when I was driving 70 miles per hour, the rock came loose and hit the inside of the wheel well of the car. How fast, in miles per hour, was the rock traveling when it came out of the tread? (The tire has a diameter of 23 inches.)
- The Giant Wheel at Cedar Point is a circle with diameter 128 feet which sits on an 8 foot tall platform making its overall height is 136 feet. It completes two revolutions in 2 minutes and 7 seconds.[15] Assuming the riders are at the edge of the circle, how fast are they traveling in miles per hour?
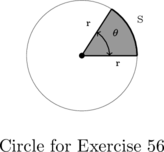
- Consider the circle of radius
 pictured below with central angle
pictured below with central angle  , measured in radians, and subtended arc of length
, measured in radians, and subtended arc of length  . Prove that the area of the shaded sector is
. Prove that the area of the shaded sector is 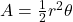 .(Hint: Use the proportion
.(Hint: Use the proportion 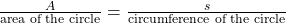 .)
.)
In Exercises 57 – 62, use the result of Exercise 56 to compute the areas of the circular sectors with the given central angles and radii.
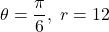
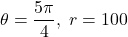
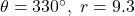
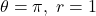
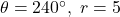
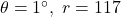
- Imagine a rope tied around the Earth at the equator. Show that you need to add only
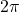 feet of length to the rope in order to lift it one foot above the ground around the entire equator. (You do NOT need to know the radius of the Earth to show this.)
feet of length to the rope in order to lift it one foot above the ground around the entire equator. (You do NOT need to know the radius of the Earth to show this.) - With the help of your classmates, look for a proof that
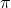 is indeed a constant.
is indeed a constant.
Section 7.1 Exercise Answers can be found in the Appendix … Coming soon
- The phrase `at least' will be justified in short order. ↵
- The choice of `
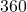 ' is most often attributed to the Babylonians. ↵
' is most often attributed to the Babylonians. ↵ - This is how a protractor is graded. ↵
- Note that by being in standard position they automatically share the same initial side which is the positive
 -axis. ↵
-axis. ↵ - It is worth noting that all of the pathologies of Analytic Trigonometry result from this fact. ↵
- Recall that this means
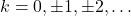 . ↵
. ↵ - The authors are well aware that we are now identifying radians with real numbers. We will justify this shortly. ↵
- This, in turn, endows the subtended arcs with an orientation as well. We address this in short order. ↵
- Note that the negative sign indicates clockwise rotation in both systems, and so it is carried along accordingly. ↵
- See Definition 3.5 in Section 3.2 for a review of this concept. ↵
- You guessed it, using Calculus
 ↵
↵ - See Example 3.2.3 in Section 3.2 for more of a discussion on instantaneous velocity. ↵
- Diagram credit: Pearson Scott Foresman [Public domain], via Wikimedia Commons. ↵
- We will discuss how we arrived at this approximation in Example 7.2.5. ↵
- Source: Cedar Point's webpage. ↵
A half-line that starts at one point and extends indefinitely from the point.
The point from which a ray starts.
The distance between two rays.
The initial point shared by two rays
The angle created when the two rays are directly opposite each other.
Two acute angles whose measures add to 90 degrees
Two angles, either two right angles or an acute angle and an obtuse angle, that add to either 180 degrees.
The ratio of the length of an arc on a circle to the radius of the circle.

