7.5 Graphs of Other Trigonometric Functions
7.5.1 Graphs of the Secant and Cosecant Functions
As mentioned at the end of Section 7.4, one way to proceed with our analysis of the circular functions is to use what we know about the functions ![]() and
and ![]() to rewrite the four additional circular functions in terms of sine and cosine with help from Theorem 7.8. We use this approach to analyze
to rewrite the four additional circular functions in terms of sine and cosine with help from Theorem 7.8. We use this approach to analyze ![]() .
.
Rewriting ![]() , we first note that
, we first note that ![]() is undefined whenever
is undefined whenever ![]() . Thanks to Example 7.2.4 number 3, we know
. Thanks to Example 7.2.4 number 3, we know ![]() whenever
whenever ![]() for integers
for integers ![]() .
.
This gives us one way to describe the domain of ![]() :
: ![]() . To get a better feel for the set of real numbers we’re dealing with, we write out and graph the domain on the number line.
. To get a better feel for the set of real numbers we’re dealing with, we write out and graph the domain on the number line.
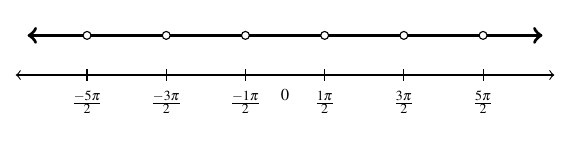
Expressing this set using interval notation is a bit of a challenge, owing to the infinitely many intervals present. As a first attempt, we have: ![]() , where, as usual, the periods of ellipsis indicate the pattern continues indefinitely. Hence, for now, it suffices to know that the domain of
, where, as usual, the periods of ellipsis indicate the pattern continues indefinitely. Hence, for now, it suffices to know that the domain of ![]() excludes the odd multiples of
excludes the odd multiples of ![]() .
.
To find the range of ![]() , we find it helpful once again to view
, we find it helpful once again to view ![]() . We know the range of
. We know the range of ![]() is
is ![]() and
and ![]() is undefined when
is undefined when ![]() , so we split our discussion into two cases: when
, so we split our discussion into two cases: when ![]() and when
and when ![]() .
.
If ![]() , then we can divide the inequality
, then we can divide the inequality ![]() by
by ![]() to obtain
to obtain ![]() . Moreover, we see as
. Moreover, we see as ![]() ,
, ![]() . If, on the other hand, if
. If, on the other hand, if ![]() , then dividing by
, then dividing by ![]() causes a reversal of the inequality so that
causes a reversal of the inequality so that ![]() . In this case, as
. In this case, as ![]() ,
, ![]() . As
. As ![]() admits all of the values in
admits all of the values in ![]() , the function
, the function ![]() admits all of the values in
admits all of the values in ![]() .
.
Because ![]() is periodic with period
is periodic with period ![]() , it shouldn’t be too surprising to find that
, it shouldn’t be too surprising to find that ![]() is also. Indeed, provided
is also. Indeed, provided ![]() and
and ![]() are defined,
are defined, ![]() if and only if
if and only if ![]() . Said differently,
. Said differently, ![]() `inherits’ its period from
`inherits’ its period from ![]() .
.
We now turn our attention to graphing ![]() . Using the table of values we tabulated when graphing
. Using the table of values we tabulated when graphing ![]() in Section 7.3, we can generate points on the graph of
in Section 7.3, we can generate points on the graph of ![]() by taking reciprocals.
by taking reciprocals.
Using the techniques developed in Section 3.2, we can more closely analyze the behavior of ![]() near the values excluded from its domain. We find as
near the values excluded from its domain. We find as ![]() ,
, ![]() , so
, so ![]() . Similarly, we get as
. Similarly, we get as ![]() ,
, ![]() ; as
; as ![]() ,
, ![]() ; and as
; and as ![]() ,
, ![]() . This means the lines
. This means the lines ![]() and
and ![]() are vertical asymptotes to the graph of
are vertical asymptotes to the graph of ![]() .
.
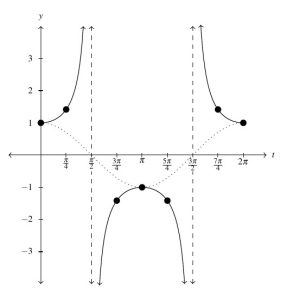
Below on the right we graph a fundamental cycle of ![]() with the graph of the fundamental cycle of
with the graph of the fundamental cycle of ![]() dotted for reference.
dotted for reference.
![Rendered by QuickLaTeX.com \[ \begin{array}{|r||r|r|r|} \hline t & \cos(t) & \sec(t) & (t,\sec(t)) \\ \hline 0 & 1 & 1 & (0,1) \\ [2pt] \hline \frac{\pi}{4} & \frac{\sqrt{2}}{2} & \sqrt{2} & \left(\frac{\pi}{4}, \sqrt{2} \right) \\ [2pt] \hline \frac{\pi}{2} & 0 & \text{undefined} & \\ [2pt] \hline \frac{3\pi}{4} & -\frac{\sqrt{2}}{2} & -\sqrt{2} & \left(\frac{3\pi}{4}, -\sqrt{2} \right) \\ [2pt] \hline \pi & -1 & -1 & (\pi, -1) \\ [2pt] \hline \frac{5\pi}{4} & -\frac{\sqrt{2}}{2} & -\sqrt{2} & \left(\frac{5\pi}{4}, -\sqrt{2} \right) \\ [2pt] \hline \frac{3\pi}{2} & 0 & \text{undefined} & \\ [2pt] \hline \frac{7\pi}{4} & \frac{\sqrt{2}}{2} & \sqrt{2} & \left(\frac{7\pi}{4}, \sqrt{2} \right) \\ [2pt] \hline 2\pi & 1 & 1& (2\pi, 1) \\ [2pt] \hline \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-3ef55914a3f79b2fbb2af20e1a7641b1_l3.png)
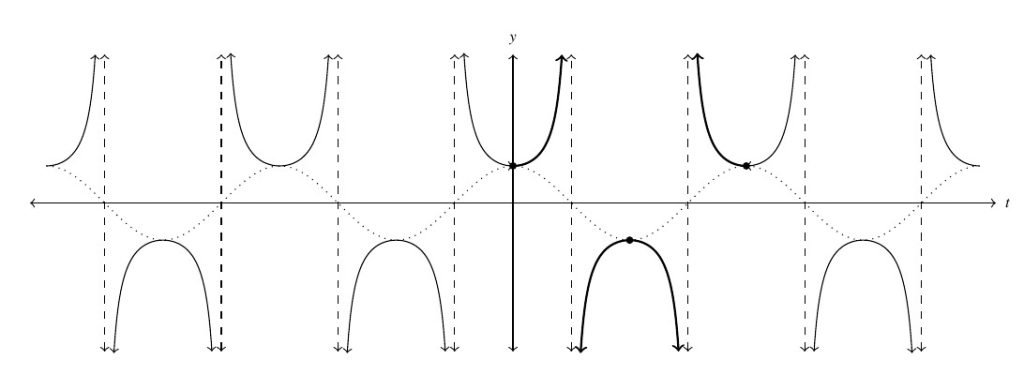
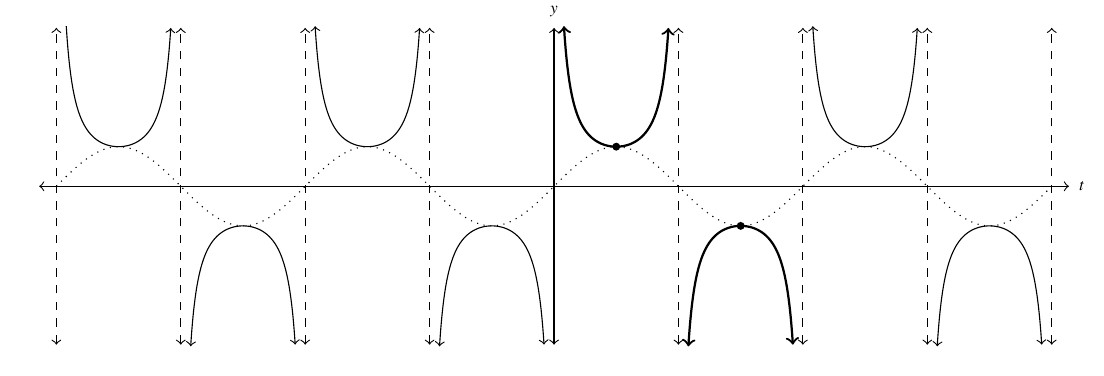
To get a graph of the entire secant function, we paste copies of the fundamental cycle end to end to produce the graph below. The graph suggests that ![]() is even. Indeed, because
is even. Indeed, because ![]() is even, that is,
is even, that is, ![]() , we have
, we have ![]() . Hence, along with its period, the secant function inherits its symmetry from the cosine function.
. Hence, along with its period, the secant function inherits its symmetry from the cosine function.
As one would expect, to graph ![]() we begin with
we begin with ![]() and take reciprocals of the corresponding
and take reciprocals of the corresponding ![]() -values. Here, we encounter issues at
-values. Here, we encounter issues at ![]() ,
, ![]() ,
, ![]() , and, in general, at all whole number multiples of
, and, in general, at all whole number multiples of ![]() , so the domain of
, so the domain of ![]() is
is ![]() . Not surprisingly, these values produce vertical asymptotes.
. Not surprisingly, these values produce vertical asymptotes.
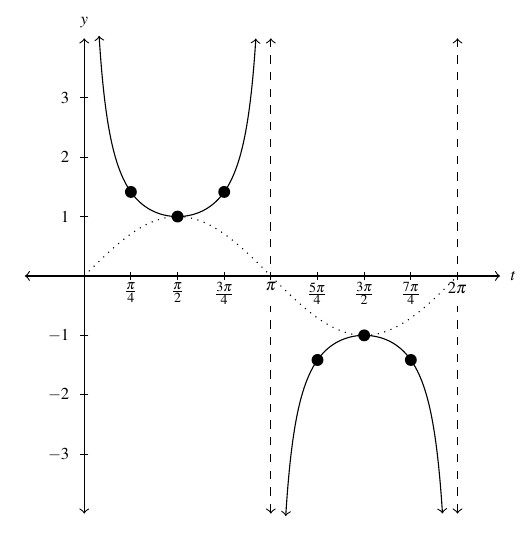
Proceeding as above, we produce the graph of the fundamental cycle of ![]() below along with the dotted graph of
below along with the dotted graph of ![]() for reference.
for reference.
![Rendered by QuickLaTeX.com \[ \begin{array}{|r||r|r|r|} \hline x & \sin(x) & \csc(x) & (x,\csc(x)) \\ \hline 0 & 0 & \text{undefined} & \\ [2pt] \hline \frac{\pi}{4} & \frac{\sqrt{2}}{2} & \sqrt{2} & \left(\frac{\pi}{4}, \sqrt{2} \right) \\ [2pt] \hline \frac{\pi}{2} & 1 & 1 & \left(\frac{\pi}{2}, 1 \right) \\ [2pt] \hline \frac{3\pi}{4} & \frac{\sqrt{2}}{2} & \sqrt{2} & \left(\frac{3\pi}{4}, \sqrt{2} \right) \\ [2pt] \hline \pi & 0 & \text{undefined} & \\ [2pt] \hline \frac{5\pi}{4} & -\frac{\sqrt{2}}{2} & -\sqrt{2} & \left(\frac{5\pi}{4}, -\sqrt{2} \right) \\ [2pt] \hline \frac{3\pi}{2} & -1 & -1 & \left(\frac{3\pi}{2},-1 \right)\\ [2pt] \hline \frac{7\pi}{4} & -\frac{\sqrt{2}}{2} & -\sqrt{2} & \left(\frac{7\pi}{4}, -\sqrt{2} \right) \\ [2pt] \hline 2\pi & 0 & \text{undefined} & \\ [2pt] \hline \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-7507b38b7998c33541d1b82a32b33ff1_l3.png)
Pasting copies of the fundamental period of ![]() end to end produces the graph below. Due to the fact that the graphs of
end to end produces the graph below. Due to the fact that the graphs of ![]() and
and ![]() are merely phase shifts of each other, it is not too surprising to find the graphs of
are merely phase shifts of each other, it is not too surprising to find the graphs of ![]() and
and ![]() are as well.
are as well.
As with the graph of secant, the graph of cosecant suggests symmetry. Indeed, as the sine function is odd, that is ![]() , so too is the cosecant function:
, so too is the cosecant function: ![]() . Hence, the graph of
. Hence, the graph of ![]() is symmetric about the origin.
is symmetric about the origin.
Note that, on the intervals between the vertical asymptotes, both ![]() and
and ![]() are continuous and smooth. In other words, they are continuous and smooth on their domains.[1]
are continuous and smooth. In other words, they are continuous and smooth on their domains.[1]
The following theorem summarizes the properties of the secant and cosecant functions. Note that all of these properties are direct results of them being reciprocals of the cosine and sine functions, respectively.
Theorem 7.11 Properties of the Secant and Cosecant Functions
- The function
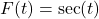
- has domain
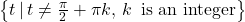
- has range
![Rendered by QuickLaTeX.com (-\infty, -1] \cup [1, \infty)](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5577aa1a2b2113c2c229739d6b58f5ca_l3.png)
- is continuous and smooth on its domain
- is even
- has period
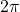
- has domain
- The function
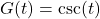
- has domain
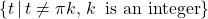
- has range
![Rendered by QuickLaTeX.com (-\infty, -1] \cup [1, \infty)](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-5577aa1a2b2113c2c229739d6b58f5ca_l3.png)
- is continuous and smooth on its domain
- is odd
- has period
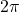
- has domain
In the next example, we discuss graphing more general secant and cosecant curves. We make heavy use of the fact they are reciprocals of sine and cosine functions and apply what we learned in Section 7.3.
Example 7.5.1
Example 7.5.1.1
Graph one cycle of the following functions. State the period of each.
![]()
Solution:
Graph one cycle of ![]() .
.
To graph ![]() , we follow the same procedure as in Example 7.3.2. That is, we use the concept of frequency and phase shift to identify quarter marks, then substitute these values into the function to obtain the corresponding points.
, we follow the same procedure as in Example 7.3.2. That is, we use the concept of frequency and phase shift to identify quarter marks, then substitute these values into the function to obtain the corresponding points.
If we think about a related cosine curve, ![]() , we know from Section 7.3, that the frequency is
, we know from Section 7.3, that the frequency is ![]() , so the period is
, so the period is ![]() .
.
![]() , so there is no phase shift.
, so there is no phase shift.
Hence, the new quarter marks for this curve are ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
These same ![]() -values are the new quarter marks for
-values are the new quarter marks for ![]() , because we obtained the fundamental cycle of the secant curve from the fundamental cycle of the cosine curve.
, because we obtained the fundamental cycle of the secant curve from the fundamental cycle of the cosine curve.
Substituting these ![]() values
values ![]() , we get the table below on the left. Note that if
, we get the table below on the left. Note that if ![]() exists, we have a point on the graph; otherwise, we have found a vertical asymptote.[2]
exists, we have a point on the graph; otherwise, we have found a vertical asymptote.[2]
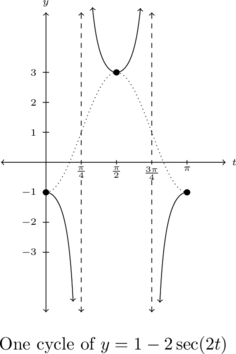
We graph one cycle of ![]() below on the right along with the associated cosine curve,
below on the right along with the associated cosine curve, ![]() which is dotted, and confirm the period is
which is dotted, and confirm the period is ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{|r||r|r|} \hline t & f(t) & (t,f(t)) \\ \hline 0 & - 1 & (0,-1) \\ [2pt] \hline \frac{\pi}{4} & \text{undefined} & \\ [2pt] \hline \frac{\pi}{2} & 3 & \left(\frac{\pi}{2}, 3 \right) \\ [2pt] \hline \frac{3\pi}{4} & \text{undefined} & \\ [2pt] \hline \pi & -1 & (\pi, -1) \\ [2pt] \hline \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-d39f9a60a6b36386f1d17e3f2a6aae2d_l3.png)
Example 7.5.1.2
Graph one cycle of the following functions. State the period of each.
![]()
Solution:
Graph one cycle ![]() .
.
As with the previous example, we start graphing ![]() by first finding the quarter marks of the associated sine curve:
by first finding the quarter marks of the associated sine curve: ![]() .
.
The coefficient of ![]() is negative, thus we make use of the odd property of sine to rewrite the function as:
is negative, thus we make use of the odd property of sine to rewrite the function as: ![]() .
.
We find the frequency is ![]() , so the period is
, so the period is ![]() .
.
![]() , so the phase shift is
, so the phase shift is ![]() .
.
Hence the fundamental cycle ![]() is shifted to the interval
is shifted to the interval ![]() with quarter marks
with quarter marks ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
Substituting these ![]() -values into
-values into ![]() , we generate the graph below on the right confirm the period is
, we generate the graph below on the right confirm the period is ![]() . The associated sine curve,
. The associated sine curve, ![]() , is dotted in as a reference.
, is dotted in as a reference.
![Rendered by QuickLaTeX.com \[ \begin{array}{|r||r|r|} \hline t & g(t) & (t,g(t)) \\ \hline -1 & \text{undefined} & \\ [2pt] \hline -\frac{1}{2} & -2 & \left(-\frac{1}{2}, -2\right) \\ [2pt] \hline 0 & \text{undefined} & \\ [2pt] \hline \frac{1}{2} & -\frac{4}{3} & \left(\frac{1}{2}, -\frac{4}{3} \right) \\ [2pt] \hline 1 & \text{undefined} & \\ [2pt] \hline \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-e6eb817b0a12fae65e38cd33fb6cabf0_l3.png)
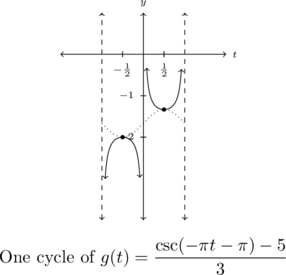
As suggested in Example 7.5.1, the concepts of frequency, period, phase shift, and baseline are alive and well with graphs of the secant and cosecant functions. The secant and cosecant curves are unbounded, therefore we do not have the concept of `amplitude’ for these curves. That being said, the amplitudes of the corresponding cosine and sine curves do play a role here – they measure how wide the gap is between the baseline and the curve.
We gather these observations in the following result whose proof is a consequence of Theorem 7.7 and is relegated to Exercise 19.
Theorem 7.12
For ![]() , the graphs of
, the graphs of
![]()
- have frequency
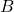
- have period
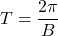
- have phase shift
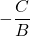
- have `baseline’
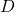 and have a vertical gap
and have a vertical gap 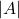 units between the the baseline and the graph[3]
units between the the baseline and the graph[3]
We put Theorem 7.12 to good use in the next example.
Example 7.5.2
Example 7.5.2.1
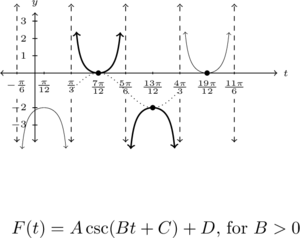
Below is the graph of one cycle of a secant (cosecant) function, ![]() .
.
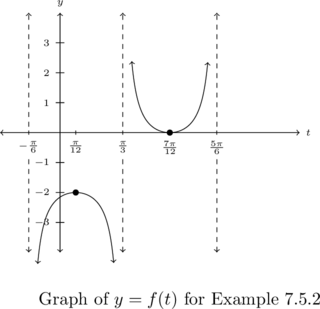
Write ![]() in the form
in the form ![]() for
for ![]() .
.
Solution:
Write ![]() in the form
in the form ![]() for
for ![]() .
.
We first note the period: ![]() and
and ![]() , so we get
, so we get ![]() .
.
To find ![]() , we need to first determine the phase shift. Recall that what is graphed here is only one cycle of the function, so by copying and pasting one more cycle, we identify what looks like a fundamental cycle of the secant function to us[4] as highlighted below on the left.
, we need to first determine the phase shift. Recall that what is graphed here is only one cycle of the function, so by copying and pasting one more cycle, we identify what looks like a fundamental cycle of the secant function to us[4] as highlighted below on the left.
We get the phase shift is ![]() so solving
so solving ![]() , we get
, we get ![]() .
.
To find the baseline, ![]() , we take a cue from our work in Example 7.3.3 in Section 7.3. We find the average of the local minimums and maximums to be
, we take a cue from our work in Example 7.3.3 in Section 7.3. We find the average of the local minimums and maximums to be ![]() , so
, so ![]() . As there is a
. As there is a ![]() unit gap between the baseline and the graph of the function, we have
unit gap between the baseline and the graph of the function, we have ![]() . Alternatively, we can sketch the corresponding cosine curve (dotted in the figure below) and determine
. Alternatively, we can sketch the corresponding cosine curve (dotted in the figure below) and determine ![]() and
and ![]() that way.
that way.
We find our final answer to be ![]() .
.
As usual, we check our answer by graphing.
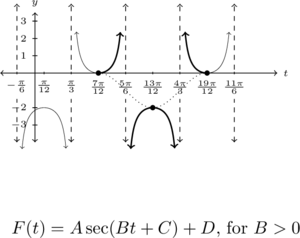
Example 7.5.2.2
Below is the graph of one cycle of a secant (cosecant) function, ![]() .
.

Write ![]() in the form
in the form ![]() for
for ![]() .
.
Solution:
Write ![]() in the form
in the form ![]() for
for ![]() .
.
The secant and cosecant curves are phase shifts of each other, therefore we could find a formula for ![]() in terms of cosecants by shifting our formula
in terms of cosecants by shifting our formula ![]() . We leave this to the reader.[5]
. We leave this to the reader.[5]
Working `from scratch,’ we would find ![]() ,
, ![]() ,
, ![]() , and
, and ![]() the same as above.[6] To determine the phase shift, we refer to the figure below.
the same as above.[6] To determine the phase shift, we refer to the figure below.
The phase shift is ![]() , thus we solve
, thus we solve ![]() to get
to get ![]() .
.
Putting all our work together, we get our final answer: ![]() .
.
Again, our best check here is to graph.
We cannot stress enough that our answers to Example 7.5.2 are one of many. For example, in Exercise 18, we ask you to rework this example choosing ![]() . It is well worth the time to think about what relationships exist between the different answers, however.
. It is well worth the time to think about what relationships exist between the different answers, however.
7.5.2 Graphs of the Tangent and Cotangent Functions
Next, we turn our attention to the tangent and cotangent functions. Viewing ![]() , we find the domain of
, we find the domain of ![]() excludes all values where
excludes all values where ![]()
Hence, the domain of ![]() is
is ![]() .
.
Using this information along with the common values we given in Section 7.4, we create the table of values below.
![Rendered by QuickLaTeX.com \[ \begin{array}{|r||r|r|} \hline t & \tan(t) & (t,\tan(t)) \\ \hline 0 & 0 & (0, 0) \\ [2pt] \hline \frac{\pi}{4} & 1 & \left(\frac{\pi}{4},1 \right) \\ [2pt] \hline \frac{\pi}{2} & \text{undefined} & \\ [2pt] \hline \frac{3\pi}{4} & -1 & \left(\frac{3\pi}{4}, -1\right) \\ [2pt] \hline \pi & 0 & (\pi, 0) \\ [2pt] \hline \frac{5\pi}{4} & 1 & \left(\frac{5\pi}{4}, 1 \right) \\ [2pt] \hline \frac{3\pi}{2} & \text{undefined} & \\ [2pt] \hline \frac{7\pi}{4} & -1 & \left(\frac{7\pi}{4}, -1 \right) \\ [2pt] \hline 2\pi & 0 & (2\pi, 0) \\ [2pt] \hline \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-400759b189f0d838995d906694271ae4_l3.png)
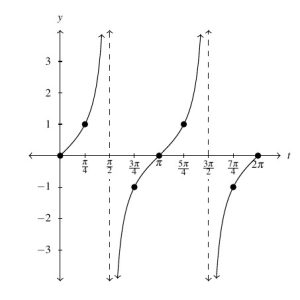
After the usual `copy and paste’ procedure, we create the graph of ![]() below:
below:
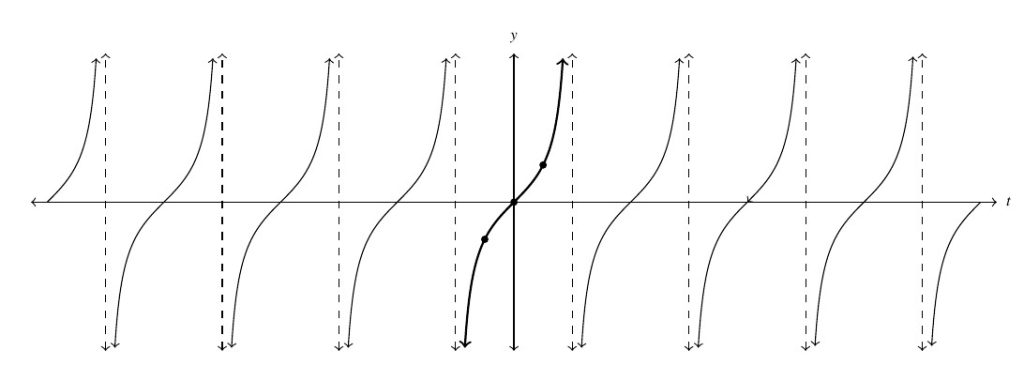
The graph of ![]() suggests symmetry through the origin. Indeed, tangent is odd because sine is odd and cosine is even:
suggests symmetry through the origin. Indeed, tangent is odd because sine is odd and cosine is even:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \tan(-t) &=& \frac{\sin(-t)}{\cos(-t)} \\[4pt] &=& \frac{-\sin(t)}{\cos(t)} \\[4pt] &=& -\tan(t) \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a34d392fc28323671095b16f7a3569ae_l3.png)
We also see the graph suggests the range of ![]() is all real numbers,
is all real numbers, ![]() . We present one proof of this fact in Exercise 18.
. We present one proof of this fact in Exercise 18.
Moreover, as noted in Section 7.4, the period of the tangent function is ![]() , and we see that reflected in the graph. This means we can choose any interval of length
, and we see that reflected in the graph. This means we can choose any interval of length ![]() to serve as our `fundamental cycle.’
to serve as our `fundamental cycle.’
We choose the cycle traced out over the (open) interval ![]() as highlighted above. In addition to the asymptotes at the endpoints
as highlighted above. In addition to the asymptotes at the endpoints ![]() , we use the `quarter marks’
, we use the `quarter marks’ ![]() and
and ![]() .
.
It should be no surprise that ![]() behaves similarly to
behaves similarly to ![]() . As
. As ![]() , the domain of
, the domain of ![]() excludes the values where
excludes the values where ![]() :
: ![]() .
.
After analyzing the behavior of ![]() near the values excluded from its domain along with plotting points, we graph
near the values excluded from its domain along with plotting points, we graph ![]() over the interval
over the interval ![]() below on the right.
below on the right.
![Rendered by QuickLaTeX.com \[ \begin{array}{|r||r|r|} \hline t & \cot(t) & (t, \cot(t)) \\ \hline 0 & \text{undefined} & \\ [2pt] \hline \frac{\pi}{4} & 1 & \left(\frac{\pi}{4},1 \right) \\ [2pt] \hline \frac{\pi}{2} & 0 & \left(\frac{\pi}{2},0 \right) \\ [2pt] \hline \frac{3\pi}{4} & -1 & \left(\frac{3\pi}{4}, -1\right) \\ [2pt] \hline \pi & \text{undefined} & \\ [2pt] \hline \frac{5\pi}{4} & 1 & \left(\frac{5\pi}{4}, 1 \right) \\ [2pt] \hline \frac{3\pi}{2} & 0 & \left(\frac{3\pi}{2}, 0 \right) \\ [2pt] \hline \frac{7\pi}{4} & -1 & \left(\frac{7\pi}{4}, -1 \right) \\ [2pt] \hline 2\pi & \text{undefined} & \\ [2pt] \hline \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-11ddd2a98e8cd4e135c2239319e4a1b4_l3.png)
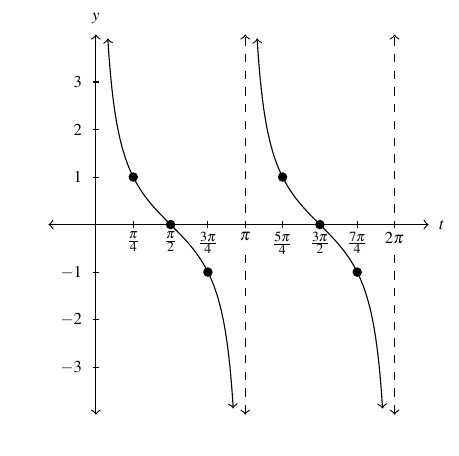
As usual, pasting copies end to end produces the graph of ![]() below.
below.
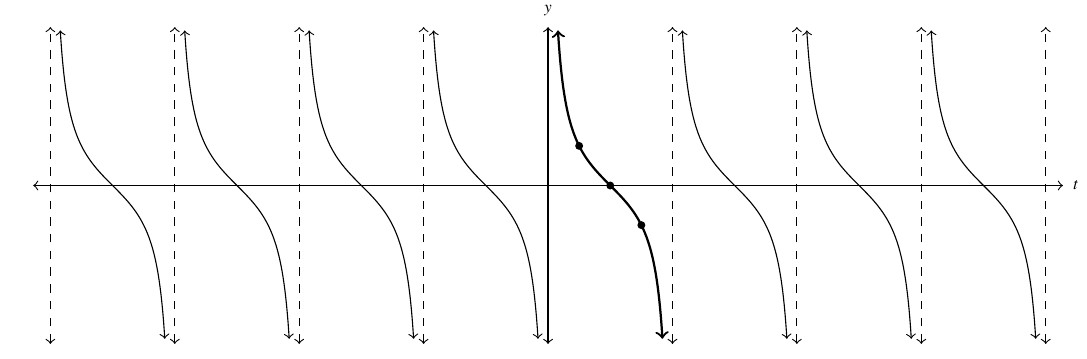
As with ![]() , the graph of
, the graph of ![]() suggests
suggests ![]() is odd, a fact we leave to the reader to prove in Exercise 22. Also, we see that the period of cotangent (like tangent) is
is odd, a fact we leave to the reader to prove in Exercise 22. Also, we see that the period of cotangent (like tangent) is ![]() and the range is
and the range is ![]()
We take as one fundamental cycle the graph as traced out over the interval ![]() , highlighted above, with quarter marks:
, highlighted above, with quarter marks: ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]()
The properties of the tangent and cotangent functions are summarized below. As with Theorem 7.11, each of the results in Theorem 7.13 can be traced back to properties of the cosine and sine functions and the definition of the tangent and cotangent functions as quotients thereof.
Theorem 7.13 Properties of the Tangent and Cotangent Functions
- The function
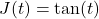
- has domain
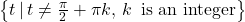
- has range

- is continuous and smooth on its domain
- is odd
- has period
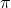
- has domain
- The function
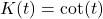
- has domain
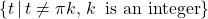
- has range

- is continuous and smooth on its domain
- is odd
- has period
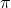
- has domain
Unlike the secant and cosecant functions, the tangent and cotangent functions have different periods than sine and cosine. Moreover, in the case of the tangent function, the fundamental cycle we’ve chosen starts at ![]() instead of
instead of ![]() . Nevertheless, we can use the same notions of period and phase shift to graph transformed versions of tangent and cotangent functions, because these results ultimately trace back to applying Theorem 1.12. We state a version of Theorem 7.7 for tangent and cotangent functions below.
. Nevertheless, we can use the same notions of period and phase shift to graph transformed versions of tangent and cotangent functions, because these results ultimately trace back to applying Theorem 1.12. We state a version of Theorem 7.7 for tangent and cotangent functions below.
Theorem 7.14
For ![]() , the functions
, the functions
![]()
- have frequency
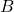
- have period
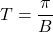
- have vertical shift or `baseline’
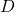
- The phase shift for
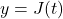 is
is 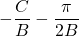
- The phase shift for
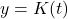 is
is 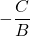
The proof of Theorem 7.14 is left to the reader in Exercise 20.
We put Theorem 7.14 to good use in the following example.
Example 7.5.3
Example 7.5.3.1
Graph one cycle of the following functions. Find the period.
![]()
Solution:
Graph one cycle of ![]() .
.
Rewriting ![]() so it fits the form in Theorem 7.14, we get
so it fits the form in Theorem 7.14, we get ![]() .
.
With ![]() , we find the period
, we find the period ![]() . As
. As ![]() , the phase shift is
, the phase shift is ![]()
Hence, one cycle of ![]() starts at
starts at ![]() and finishes at
and finishes at ![]() . Our quarter marks are
. Our quarter marks are ![]() units apart and are
units apart and are ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and, finally,
, and, finally, ![]()
Substituting these ![]() -values into
-values into ![]() , we find points on the graph and the vertical asymptotes.[7]
, we find points on the graph and the vertical asymptotes.[7]
![Rendered by QuickLaTeX.com \[ \begin{array}{|r||r|r|} \hline t & f(t) & (t,f(t)) \\ \hline \pi & \text{undefined} & \\ [2pt] \hline \frac{3\pi}{2} & 2 & \left(\frac{3\pi}{2}, 2 \right) \\ [2pt] \hline 2 \pi & 1 & (2\pi,1) \\ [2pt] \hline \frac{5\pi}{2} & 0 & \left(\frac{5\pi}{2}, 0 \right) \\ [2pt] \hline 3 \pi & \text{undefined} & \\ [2pt] \hline \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c8e6c20ac143fe458a161b9846a07916_l3.png)
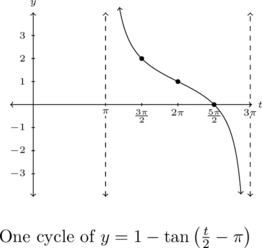
We confirm that the period is ![]() .
.
Example 7.5.3.2
Graph one cycle of the following functions. Find the period.
![]()
Solution:
Graph one cycle of ![]() .
.
To put ![]() into the form prescribed by Theorem 7.14, we make use of the odd property of cotangent:
into the form prescribed by Theorem 7.14, we make use of the odd property of cotangent:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} g(t) &=& 2\cot\left(2\pi - \pi t \right) - 1 \\ & =& 2\cot( -[\pi t- 2\pi]) - 1 \\ &=& -2 \cot(\pi t- 2\pi) - 1 \\ &=& -2 \cot(\pi t + (- 2\pi)) - 1 \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-88b1f978c8d64188af8e34b0e721c0e5_l3.png)
We identify ![]() so the period is
so the period is ![]() . Because
. Because ![]() , the phase shift is
, the phase shift is ![]() . Hence, one cycle of
. Hence, one cycle of ![]() starts at
starts at ![]() and ends at
and ends at ![]() .
.
Our quarter marks are ![]() units apart and are
units apart and are ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . We generate the next graph.
. We generate the next graph.
![Rendered by QuickLaTeX.com \[ \begin{array}{|r||r|r|} \hline t & g(t) & (t,g(t)) \\ \hline 2 & \text{undefined} & \\ [2pt] \hline \frac{9}{4} & -3 & \left(\frac{9}{4}, -3 \right) \\ [2pt] \hline \frac{5}{2} & -1 & \left( \frac{5}{2}, -1 \right) \\ [2pt] \hline \frac{11}{4} & 1 & \left(\frac{11}{4}, 1 \right) \\ [2pt] \hline 3 & \text{undefined} & \\ [2pt] \hline \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-1a909deb5ac77ea9068d9869c65cc313_l3.png)
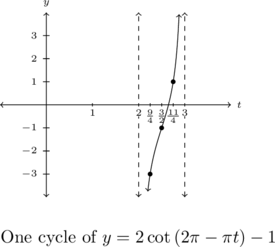
We confirm the period is ![]() .
.
Example 7.5.4
Example 7.5.4.1
Below is the graph of one cycle of a tangent (cotangent) function, ![]() .
.
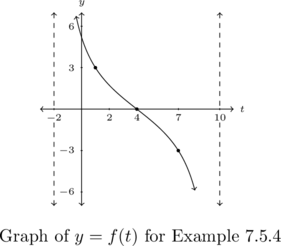
Write ![]() in the form
in the form ![]() for
for ![]() .
.
Solution:
Write ![]() in the form
in the form ![]() for
for ![]() .
.
We first find the period ![]() . Per Theorem 7.14, we know
. Per Theorem 7.14, we know ![]() , or
, or ![]() .
.
Next, we look for the phase shift. We notice the cycle graphed for us is decreasing instead of the usual increasing we expect for a standard tangent cycle. When this sort of thing happened in Examples 7.3.3 and 7.5.2, we pasted another cycle of the function and used that to help identify the phase shift in order to keep the value of ![]() . Here, no amount of `copying and pasting’ will produce an increasing cycle (do you see why?), so we know
. Here, no amount of `copying and pasting’ will produce an increasing cycle (do you see why?), so we know ![]() and use
and use ![]() , as the phase shift.
, as the phase shift.
The formula given in Theorem 7.14 tells us ![]() so substituting
so substituting ![]() gives
gives ![]() .
.
Next, we see the baseline here is still the ![]() -axis, so
-axis, so ![]() .
.
This means all that’s left to find is ![]() . We have already established that
. We have already established that ![]() to account for the reflection across the
to account for the reflection across the ![]() -axis. Moreover, the
-axis. Moreover, the ![]() -values of the points off of the baseline are
-values of the points off of the baseline are ![]() units from the baseline, indicating a vertical stretch by a factor of
units from the baseline, indicating a vertical stretch by a factor of ![]() .
.
Hence, ![]() and
and ![]() .
.
As usual, the ultimate check is to graph, which we will leave to the reader.
Example 7.5.4.2
Below is the graph of one cycle of a tangent (cotangent) function, ![]() .
.

Write ![]() in the form
in the form ![]() for
for ![]() .
.
Solution:
Write ![]() in the form
in the form ![]() for
for ![]() .
.
We find ![]() ,
, ![]() , and
, and ![]() as above. As the fundamental cycle of cotangent is decreasing, we know
as above. As the fundamental cycle of cotangent is decreasing, we know ![]() and identify the phase shift as
and identify the phase shift as ![]() .
.
Using Theorem 7.14, we know ![]() so substituting
so substituting ![]() , we get
, we get ![]() .
.
As above, the vertical stretch is by a factor of ![]() , so we take
, so we take ![]() for our final answer:
for our final answer: ![]() .
.
We leave it to the reader to check our answer by graphing.
Once again, our answers to Example 7.5.4 are one of many, and we invite the reader to think about what all of the solutions would have in common. We close this section with an application.
Example 7.5.5
Example 7.5.5.1
Let ![]() be the angle of inclination from an observation point on the ground 42 feet away from the launch site of a model rocket. Assuming the rocket is launched directly upwards:
be the angle of inclination from an observation point on the ground 42 feet away from the launch site of a model rocket. Assuming the rocket is launched directly upwards:
Write a formula for ![]() , the distance from the rocket to the ground (in feet) as a function of
, the distance from the rocket to the ground (in feet) as a function of ![]() . Compute and interpret
. Compute and interpret ![]() .
.
Solution:
We begin by sketching the scenario below. Given the rocket is launched `directly upwards,’ we may assume the rocket is launched at a ![]() angle which provides us with a right triangle.
angle which provides us with a right triangle.
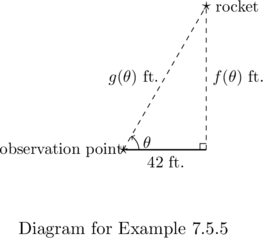
Write a formula for ![]() , the distance from the rocket to the ground (in feet) as a function of
, the distance from the rocket to the ground (in feet) as a function of ![]() . Compute and interpret
. Compute and interpret ![]() .
.
From the remarks preceding Theorem 7.10, we know the definitions of the circular functions agree with those specified for acute angles in right triangles as described in Definition 7.6 in Section 7.2.1.
Hence, ![]() , so
, so ![]() .
.
We find ![]() . This means when the angle of inclination is
. This means when the angle of inclination is ![]() or
or ![]() , the rocket is or
, the rocket is or ![]() feet off of the ground.
feet off of the ground.
Example 7.5.5.2
Let ![]() be the angle of inclination from an observation point on the ground 42 feet away from the launch site of a model rocket. Assuming the rocket is launched directly upwards:
be the angle of inclination from an observation point on the ground 42 feet away from the launch site of a model rocket. Assuming the rocket is launched directly upwards:
Write a formula for ![]() , the distance from the rocket to the observation point on the ground (in feet) as a function of
, the distance from the rocket to the observation point on the ground (in feet) as a function of ![]() . Compute and interpret
. Compute and interpret ![]() .
.
Solution:
We begin by sketching the scenario below. Given the rocket is launched `directly upwards,’ we may assume the rocket is launched at a ![]() angle which provides us with a right triangle.
angle which provides us with a right triangle.

Write a formula for ![]() , the distance from the rocket to the observation point on the ground (in feet) as a function of
, the distance from the rocket to the observation point on the ground (in feet) as a function of ![]() . Compute and interpret
. Compute and interpret ![]() .
.
Again, working with the triangle, we find ![]() so that
so that ![]() .
.
We find ![]() , so when the angle of inclination is
, so when the angle of inclination is ![]() , the rocket is
, the rocket is ![]() feet from the observation point on the ground.
feet from the observation point on the ground.
Example 7.5.5.3
Let ![]() be the angle of inclination from an observation point on the ground 42 feet away from the launch site of a model rocket. Assuming the rocket is launched directly upwards:
be the angle of inclination from an observation point on the ground 42 feet away from the launch site of a model rocket. Assuming the rocket is launched directly upwards:
Write and interpret the behavior of ![]() and
and ![]() as
as ![]() .
.
Solution:
We begin by sketching the scenario below. Given the rocket is launched `directly upwards,’ we may assume the rocket is launched at a ![]() angle which provides us with a right triangle.
angle which provides us with a right triangle.

Write and interpret the behavior of ![]() and
and ![]() as
as ![]() .
.
As ![]() , both
, both ![]() and
and ![]() (a fact we could verify graphically, if needs be.)
(a fact we could verify graphically, if needs be.)
This means as the angle of inclination approaches ![]() or
or ![]() , the distances from the rocket to the ground and from to the rocket to the observation point increase without bound. Barring the effects of drift or the curvature of space, this matches our intuition.
, the distances from the rocket to the ground and from to the rocket to the observation point increase without bound. Barring the effects of drift or the curvature of space, this matches our intuition.
7.5.3 Section Exercises
In Exercises 1 – 12, graph one cycle of the given function. State the period of the function.
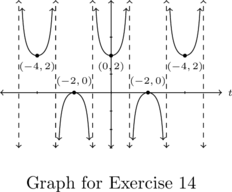
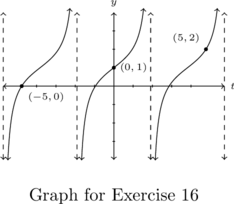
In Exercises 13 – 14, the graph of a (co)secant function is given. Write a formula for the function in the form ![]() and
and ![]() . Select
. Select ![]() so
so ![]() . Check your answer by graphing.
. Check your answer by graphing.
- Asymptotes:
 ,
,  ,
, 
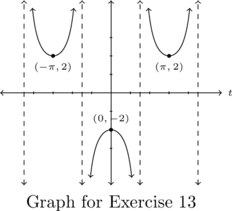
- Asymptotes:
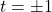 ,
, 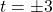 ,
, 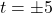 ,
, 
In Exercises 15 – 16, the graph of a (co)tangent function given. Find a formula the function in the form ![]() and
and ![]() . Select
. Select ![]() so
so ![]() . Check your answer by graphing.
. Check your answer by graphing.
- Asymptotes:
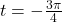 ,
, 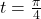 ,
, 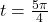 ,
, 
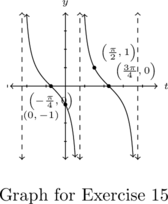
- Asymptotes:
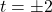 ,
, 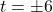 ,
, 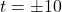 ,
, 
- (a) Use the conversion formulas listed in Theorem 7.6 to create conversion formulas between secant and cosecant functions.
(b) Use a conversion formula to rewrite our first answer to Example 7.5.2,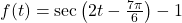 , in terms of cosecants.
, in terms of cosecants. - Rework Example 7.5.2 and find answers with
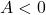 .
. - Prove Theorem 7.12 using Theorem 7.7.
- Prove Theorem 7.14 using Theorem 1.12.
- In this Exercise, we argue the range of the tangent function is
 . Let
. Let 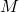 be a fixed, but arbitrary positive real number.
be a fixed, but arbitrary positive real number.
- Show there is an acute angle
 with
with 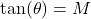 . (Hint: think right triangles.)
. (Hint: think right triangles.) - Using the symmetry of the Unit Circle, explain why there are angles
 with
with 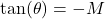 .
. - Determine angles with
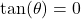 .
. - Combine the three parts above to conclude the range of the tangent function is
 .
.
- Show there is an acute angle
- Prove
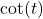 is odd. (Hint: mimic the proof given in the text that
is odd. (Hint: mimic the proof given in the text that 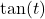 is odd.)
is odd.)
Section 7.5 Exercise Answers can be found in the Appendix … Coming soon
- Just like the rational functions in Chapter 3 are continuous and smooth on their domains because polynomials are continuous and smooth everywhere, the secant and cosecant functions are continuous and smooth on their domains as a result of the cosine and sine functions are continuous and smooth everywhere. ↵
- As with the examples in Section 7.3, note that we can partially check our answer because the argument of the secant function should simplify to the `original' quarter marks - the quadrantal angles. ↵
- In other words, the range of these functions is
![Rendered by QuickLaTeX.com (-\infty, D-|A|] \cup [D+|A|, \infty)](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-52c9224b1521f7930b9ffd709a8c63c7_l3.png) . ↵
. ↵ - Assuming
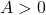 , that is. ↵
, that is. ↵ - See Exercise 17. ↵
- Again, assuming we want
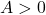 . ↵
. ↵ - Here, as with all tangent functions, we can partially check our new quarter marks by noting the argument of the tangent function simplifies, in each case, to one of the original quarter marks of the interval
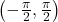 . ↵
. ↵

