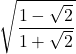0.1 Real Numbers and Exponents
In this section we list the properties of real number arithmetic. This is meant to be a succinct, targeted review so we’ll resist the temptation to wax poetic about these axioms and their subtleties and refer the interested reader to a more formal course in Abstract Algebra.
0.1.1 Sets of Real Numbers
The playground for most of this text is the set of Real Numbers. Much of the “real world” can be quantified using real numbers: the temperature at a given time, the revenue generated by selling a certain number of products and the maximum population of Sasquatch which can inhabit a particular region are just three basic examples. A succinct, but nonetheless incomplete[1] definition of a real number is given below.
Definition 0.1
A real number is any number which possesses a decimal representation. The set of real numbers is denoted by the character ![]() .
.
Certain subsets of the real numbers are worthy of note and are listed below. In fact, in more advanced texts,[2] the real numbers are constructed from some of these subsets.
Special Subsets of Real Numbers
- The Natural Numbers:
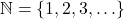 . The periods of ellipsis `
. The periods of ellipsis ` ‘ here indicate that the natural numbers contain 1, 2, 3 `and so forth’.
‘ here indicate that the natural numbers contain 1, 2, 3 `and so forth’. - The Whole Numbers:
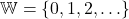 .
. - The Integers:
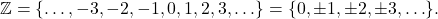 [3]
[3] - The Rational Numbers:
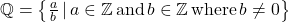 . Rational numbers are the ratios of integers where the denominator is not zero. It turns out that another way to describe the rational numbers is:
. Rational numbers are the ratios of integers where the denominator is not zero. It turns out that another way to describe the rational numbers is: 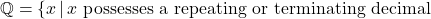
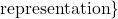
- The Irrational Numbers:
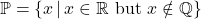 . That is, an irrational number is a real number, which isn’t rational. Said differently,
. That is, an irrational number is a real number, which isn’t rational. Said differently, 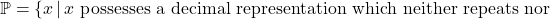
Note that every natural number is a whole number which, in turn, is an integer. Each integer is a rational number (take ![]() in the above definition for
in the above definition for ![]() ) and because every rational number is a real number the sets
) and because every rational number is a real number the sets ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are nested like Matryoshka dolls. More formally, these sets form a subset chain:
are nested like Matryoshka dolls. More formally, these sets form a subset chain: ![]() . The reader is encouraged to sketch a Venn Diagram depicting
. The reader is encouraged to sketch a Venn Diagram depicting ![]() and all of the subsets mentioned above.
and all of the subsets mentioned above.
There are two primary operations one can perform with real numbers: addition and multiplication. We’ll start with the properties of addition.
Properties of Real Number Addition
- Closure: For all real numbers
 and
and  ,
, 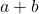 is also a real number.
is also a real number. - Commutativity: For all real numbers
 and
and  ,
,  .
. - Associativity: For all real numbers
 ,
,  and
and  ,
, 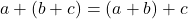 .
. - Identity: There is a real number `
 ‘ so that for all real numbers
‘ so that for all real numbers  ,
, 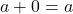 .
. - Inverse: For all real numbers
 , there is a real number
, there is a real number 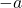 such that
such that 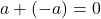 .
. - Definition of Subtraction: For all real numbers
 and
and  ,
, 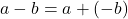 .
.
Next, we give real number multiplication a similar treatment. Recall that we may denote the product of two real numbers ![]() and
and ![]() a variety of ways:
a variety of ways: ![]() ,
, ![]() ,
, ![]() ,
, ![]() and so on. We’ll refrain from using
and so on. We’ll refrain from using ![]() for real number multiplication in this text with one notable exception, when defining scientific notation.
for real number multiplication in this text with one notable exception, when defining scientific notation.
Properties of Real Number Multiplication
- Closure: For all real numbers
 and
and  ,
, 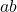 is also a real number.
is also a real number. - Commutativity: For all real numbers
 and
and  ,
, 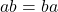 .
. - Associativity: For all real numbers
 ,
,  and
and  ,
, 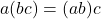 .
. - Identity: There is a real number `
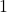 ‘ so that for all real numbers
‘ so that for all real numbers  ,
, 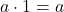 .
. - Inverse: For all real numbers
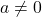 , there is a real number
, there is a real number  such that
such that 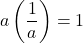 .
. - Definition of Division: For all real numbers
 and
and 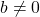 ,
, 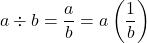 .
.
While most students and some faculty tend to skip over these properties or give them a cursory glance at best, it is important to realize that the properties stated above are what drive the symbolic manipulation in all of Algebra. When listing a tally of more than two numbers, ![]() for example, we don’t need to specify the order in which those numbers are added. Notice though, try as we might, we can add only two numbers at a time and it is the associative property of addition which assures us that we could organize this sum as
for example, we don’t need to specify the order in which those numbers are added. Notice though, try as we might, we can add only two numbers at a time and it is the associative property of addition which assures us that we could organize this sum as ![]() or
or ![]() . This brings up a note about `grouping symbols’. Recall that parentheses and brackets are used in order to specify which operations are to be performed first. In the absence of such grouping symbols, multiplication (and hence division) is given priority over addition (and hence subtraction). For example,
. This brings up a note about `grouping symbols’. Recall that parentheses and brackets are used in order to specify which operations are to be performed first. In the absence of such grouping symbols, multiplication (and hence division) is given priority over addition (and hence subtraction). For example, ![]() , but
, but ![]() . As you may recall, we can `distribute’ the
. As you may recall, we can `distribute’ the ![]() across the addition if we really wanted to do the multiplication first:
across the addition if we really wanted to do the multiplication first: ![]() . More generally, we have the following.
. More generally, we have the following.
The Distributive Property and Factoring
For all real numbers ![]() ,
, ![]() and
and ![]() :
:
- Distributive Property:
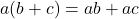 and
and 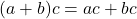 .
. - Factoring:
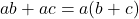 and
and 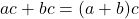 .
.
Properties of Zero
Suppose ![]() and
and ![]() are real numbers.
are real numbers.
- Zero Product Property:
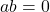 if and only if
if and only if 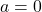 or
or 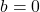 (or both)
(or both)
Note: This not only says that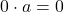 for any real number
for any real number  , it also says that the only way to get an answer of `
, it also says that the only way to get an answer of ` ‘ when multiplying two real numbers is to have one (or both) of the numbers be `
‘ when multiplying two real numbers is to have one (or both) of the numbers be ` ‘ in the first place.
‘ in the first place. - Zeros in Fractions: If
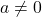 ,
, 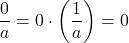 .
.
Note: The quantity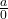 is undefined.[4]
is undefined.[4]
The Zero Product Property drives most of the equation solving algorithms in Algebra because it allows us to take complicated equations and reduce them to simpler ones. For example, you may recall that one way to solve ![]() is by factoring[5] the left hand side of this equation to get
is by factoring[5] the left hand side of this equation to get ![]() . From here, we apply the Zero Product Property and set each factor equal to zero. This yields
. From here, we apply the Zero Product Property and set each factor equal to zero. This yields ![]() or
or ![]() so
so ![]() or
or ![]() . This application to solving equations leads, in turn, to some deep and profound structure theorems in Chapter 2.
. This application to solving equations leads, in turn, to some deep and profound structure theorems in Chapter 2.
Next up is a review of the arithmetic of ‘negatives’. We previously introduced the dash which we all recognize as the `negative’ symbol in terms of the additive inverse. For example, the number ![]() (read `negative
(read `negative ![]() ‘) is defined so that
‘) is defined so that ![]() . We then defined subtraction using the concept of the additive inverse again so that, for example,
. We then defined subtraction using the concept of the additive inverse again so that, for example, ![]() . In this text we do not distinguish typographically between the dashes in the expressions `
. In this text we do not distinguish typographically between the dashes in the expressions `![]() ‘ and `
‘ and `![]() ‘ even though they are mathematically quite different.[6] In the expression `
‘ even though they are mathematically quite different.[6] In the expression `![]() ,’ the dash is a binary operation (that is, an operation requiring two numbers) whereas in `
,’ the dash is a binary operation (that is, an operation requiring two numbers) whereas in `![]() ‘, the dash is a unary operation (that is, an operation requiring only one number). You might ask, `Who cares?’ Your calculator does – that’s who! In the text we can write
‘, the dash is a unary operation (that is, an operation requiring only one number). You might ask, `Who cares?’ Your calculator does – that’s who! In the text we can write ![]() but that will not work in your calculator. Instead you’d need to type
but that will not work in your calculator. Instead you’d need to type ![]() to get
to get ![]() where the first dash comes from the `
where the first dash comes from the `![]() ‘ key and the second dash comes from the subtraction key.
‘ key and the second dash comes from the subtraction key.
Properties of Negatives
Given real numbers ![]() and
and ![]() we have the following.
we have the following.
- Additive Inverse Properties:
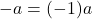 and
and 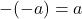
- Products of Negatives:
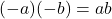 .
. - Negatives and Products:
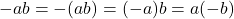 .
. - Negatives and Fractions: If
 is nonzero,
is nonzero, 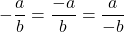 and
and 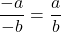 .
. - `Distributing‘ Negatives:
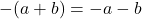 and
and 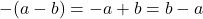 .
. - `Factoring‘ Negatives:
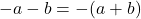 and
and 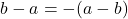 .
.
An important point here is that when we `distribute’ negatives, we do so across addition or subtraction only. This is because we are really distributing a factor of ![]() across each of these terms:
across each of these terms: ![]() . Negatives do not `distribute’ across multiplication:
. Negatives do not `distribute’ across multiplication: ![]() . Instead,
. Instead, ![]() .
.
The same sort of thing goes for fractions: ![]() can be written as
can be written as ![]() or
or ![]() , but not
, but not ![]() .
.
Speaking of fractions, we now review their arithmetic.
Properties of Fractions
- Identity Properties:
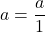 and
and 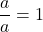 .
. - Fraction Equality:
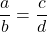 if and only if
if and only if 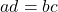 .
. - Multiplication of Fractions:
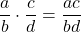 .
.
In particular: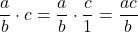
Note: A common denominator is not required to multiply fractions! - Division[7] of Fractions:
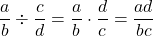 .
.
In particular: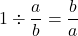 and
and 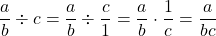
Note: A common denominator is not required to divide fractions! - Addition and Subtraction of Fractions:
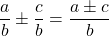 .
.
Note: A common denominator is required to add or subtract fractions! - Equivalent Fractions:
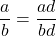 , as
, as 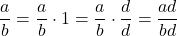
Note: The only way to change the denominator is to multiply both it and the numerator by the same nonzero value because we are, in essence, multiplying the fraction by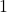 .
. - `Reducing‘[8] Fractions:
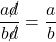 , as
, as 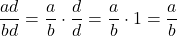 .
.
In particular,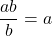 as
as 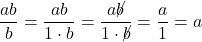 and
and 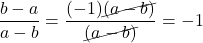 .
.
Note: We may only cancel common factors from both numerator and denominator.
Students make so many mistakes with fractions that we feel it is necessary to pause the narrative for a moment and offer you the following examples. Please take the time to read these carefully. In the main body of the text we will skip many of the steps shown here and it is your responsibility to understand the arithmetic behind the computations we use throughout the text. We deliberately limited these examples to “nice” numbers (meaning that the numerators and denominators of the fractions are small integers) and will discuss more complicated matters later. In the upcoming example, we will make use of the Fundamental Theorem of Arithmetic which essentially says that every natural number has a unique prime factorization. Thus `lowest terms’ is clearly defined when reducing the fractions you’re about to see.
Example 0.1.1
Example 0.1.1.1
Perform the indicated operations and simplify. By `simplify’ here, we mean to have the final answer written in the form ![]() where
where ![]() and
and ![]() are integers which have no common factors. Said another way, we want
are integers which have no common factors. Said another way, we want ![]() in `lowest terms’.
in `lowest terms’.
![]()
Solution:
Simplify ![]() .
.
It may seem silly to start with an example this basic but experience has taught us not to take much for granted. We start by identifying the lowest common denominator and then we rewrite the fractions using that new denominator. As ![]() and
and ![]() are relatively prime, meaning they have no factors in common, the lowest common denominator is
are relatively prime, meaning they have no factors in common, the lowest common denominator is ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{1}{4} + \dfrac{6}{7} & = & \dfrac{1}{4} \cdot \dfrac{7}{7} + \dfrac{6}{7} \cdot \dfrac{4}{4} & \text{Equivalent Fractions} \\ [10pt] & = & \dfrac{7}{28} + \dfrac{24}{28} & \text{Multiplication of Fractions}\\ [10pt] & = & \dfrac{31}{28}& \text{Addition of Fractions} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-1649b7060a42953287d9c1a53fb59a3a_l3.png)
The result is in lowest terms because ![]() and
and ![]() are relatively prime so we’re done.
are relatively prime so we’re done.
Example 0.1.1.2
Perform the indicated operations and simplify. By `simplify’ here, we mean to have the final answer written in the form ![]() where
where ![]() and
and ![]() are integers which have no common factors. Said another way, we want
are integers which have no common factors. Said another way, we want ![]() in `lowest terms’.
in `lowest terms’.
![]()
Solution:
Simplify ![]() .
.
We could begin with the subtraction in parentheses, namely ![]() , and then subtract that result from
, and then subtract that result from ![]() . It’s easier, however, to first distribute the negative across the quantity in parentheses and then use the Associative Property to perform all of the addition and subtraction in one step.[9] The lowest common denominator[10] for all three fractions is
. It’s easier, however, to first distribute the negative across the quantity in parentheses and then use the Associative Property to perform all of the addition and subtraction in one step.[9] The lowest common denominator[10] for all three fractions is ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{5}{12} - \left(\dfrac{47}{30} - \dfrac{7}{3}\right) & = & \dfrac{5}{12} - \dfrac{47}{30} + \dfrac{7}{3} & \text{Distribute the Negative}\\[10pt] & = & \dfrac{5}{12} \cdot \dfrac{5}{5} - \dfrac{47}{30} \cdot \dfrac{2}{2} + \dfrac{7}{3} \cdot \dfrac{20}{20} & \text{Equivalent Fractions}\\[10pt] & = & \dfrac{25}{60} - \dfrac{94}{60} + \dfrac{140}{60} & \text{Multiplication of Fractions} \\[10pt] & = & \dfrac{71}{60} & \text{Addition and Subtraction of Fractions} \\[10pt] \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-31829b40b7add567a0c5328223502ffc_l3.png)
The numerator and denominator are relatively prime so the fraction is in lowest terms and we have our final answer.
Example 0.1.1.3
Perform the indicated operations and simplify. By `simplify’ here, we mean to have the final answer written in the form ![]() where
where ![]() and
and ![]() are integers which have no common factors. Said another way, we want
are integers which have no common factors. Said another way, we want ![]() in `lowest terms’.
in `lowest terms’.
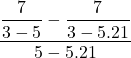 .
.
Solution:
Simplify 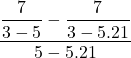 .
.
What we are asked to simplify in this problem is known as a `complex’ or `compound’ fraction. Simply put, we have fractions within a fraction. The longest division line[11] acts as a grouping symbol, quite literally dividing the compound fraction into a numerator (containing fractions) and a denominator (which in this case does not contain fractions). The first step to simplifying a compound fraction like this one is to see if you can simplify the little fractions inside it. To that end, we clean up the fractions in the numerator as follows.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{\dfrac{7}{3-5} - \dfrac{7}{3-5.21}}{5-5.21} & = & \dfrac{\dfrac{7}{-2} - \dfrac{7}{-2.21}}{-0.21} & \\ [10pt] & = & \dfrac{-\left(-\dfrac{7}{2} + \dfrac{7}{2.21}\right)}{0.21} & \text{Properties of Negatives} \\ [10pt] & = & \dfrac{\dfrac{7}{2} - \dfrac{7}{2.21}}{0.21} & \text{Distribute the Negative} \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-1384f71142c1a90c3385ac194b110772_l3.png)
We are left with a compound fraction with decimals. We could replace ![]() with
with ![]() but that would make a mess.[12] It’s better in this case to eliminate the decimal in the numerator by multiplying the numerator and denominator of the fraction with the decimal in it by
but that would make a mess.[12] It’s better in this case to eliminate the decimal in the numerator by multiplying the numerator and denominator of the fraction with the decimal in it by ![]() (because
(because ![]() is an integer) as shown below.
is an integer) as shown below.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclrr} \dfrac{\dfrac{7}{2} - \dfrac{7}{2.21}}{0.21} & = & \dfrac{ \dfrac{7}{2} - \dfrac{7 \cdot 100}{2.21 \cdot 100}}{0.21} & \quad &\\[12pt] & = & \dfrac{\dfrac{7}{2} - \dfrac{700}{221}}{0.21} & \quad &\\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-bd0dfdeb34b1c2d8af0cec50e11b78b4_l3.png)
We now perform the subtraction in the numerator and replace ![]() with
with ![]() in the denominator. This will leave us with one fraction divided by another fraction. We finish by performing the `division by a fraction is multiplication by the reciprocal’ concept and then cancel any factors that we can.
in the denominator. This will leave us with one fraction divided by another fraction. We finish by performing the `division by a fraction is multiplication by the reciprocal’ concept and then cancel any factors that we can.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{\dfrac{7}{2}-\dfrac{700}{221}}{0.21} & = & \dfrac{\dfrac{7}{2}\cdot\dfrac{221}{221} - \dfrac{700}{221}\cdot\dfrac{2}{2}}{\dfrac{21}{100}} & \vphantom{\dfrac{\dfrac{12}{5} - \dfrac{7}{24}}{1 + \left(\dfrac{12}{5}\right) \left(\dfrac{7}{24}\right)}} \\[15pt] & = & \dfrac{\dfrac{1547}{442} -\dfrac{1400}{442}}{\dfrac{21}{100}} & \vphantom{\dfrac{\dfrac{12}{5} - \dfrac{7}{24}}{1 + \left(\dfrac{12}{5}\right) \left(\dfrac{7}{24}\right)}}\\[15pt] & = & \dfrac{\dfrac{147}{442}}{\dfrac{21}{100}} = \dfrac{147}{442} \cdot \dfrac{100}{21} & \vphantom{\dfrac{\dfrac{12}{5} - \dfrac{7}{24}}{1 + \left(\dfrac{12}{5}\right) \left(\dfrac{7}{24}\right)}} \\[15pt] & = & \dfrac{14700}{9282} = \dfrac{350}{221} &\\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-dba9d2c3467ea0fdfc380df59b91fbe2_l3.png)
The last step comes from the factorizations ![]() and
and ![]() .
.
Example 0.1.1.4
Perform the indicated operations and simplify. By `simplify’ here, we mean to have the final answer written in the form ![]() where
where ![]() and
and ![]() are integers which have no common factors. Said another way, we want
are integers which have no common factors. Said another way, we want ![]() in `lowest terms’.
in `lowest terms’.
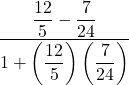
Solution:
Simplify 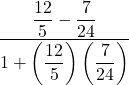 .
.
We are given another compound fraction to simplify and this time both the numerator and denominator contain fractions. As before, the longest division line acts as a grouping symbol to separate the numerator from the denominator.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{\dfrac{12}{5} - \dfrac{7}{24}}{1 + \left(\dfrac{12}{5}\right) \left(\dfrac{7}{24}\right)} & = & \dfrac{\left(\dfrac{12}{5} - \dfrac{7}{24}\right)}{\left(1 + \left(\dfrac{12}{5}\right) \left(\dfrac{7}{24}\right)\right)} & \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-4023349a0d06f44f78a6af37be051edb_l3.png)
Hence, one way to proceed is as before: simplify the numerator and the denominator then perform the `division by a fraction is the multiplication by the reciprocal’ concept. While there is nothing wrong with this approach, we’ll use our Equivalent Fractions property to rid ourselves of the `compound’ nature of this fraction straight away. The idea is to multiply both the numerator and denominator by the lowest common denominator of each of the `smaller’ fractions – in this case, ![]() .
.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{\left(\dfrac{12}{5} - \dfrac{7}{24}\right)}{\left(1 + \left(\dfrac{12}{5}\right) \left(\dfrac{7}{24}\right)\right)} & = &\dfrac{\left(\dfrac{12}{5} - \dfrac{7}{24}\right) \cdot 120}{\left(1 + \left(\dfrac{12}{5}\right) \left(\dfrac{7}{24}\right)\right) \cdot 120} & \text{Equivalent Fractions}\\ [30pt] & = & \dfrac{\left(\dfrac{12}{5}\right) (120) - \left(\dfrac{7}{24}\right) (120)}{(1)(120) + \left(\dfrac{12}{5}\right) \left(\dfrac{7}{24}\right)(120)} & \text{Distributive Property} \\[30pt] & = & \dfrac{\dfrac{12 \cdot 120}{5} - \dfrac{7 \cdot 120}{24}}{120 + \dfrac{12 \cdot 7 \cdot 120}{5 \cdot 24}} & \text{Multiply fractions} \\ [25pt] & = & \dfrac{\dfrac{12 \cdot 24 \cdot \cancel{5}}{\cancel{5}} - \dfrac{7 \cdot 5 \cdot \cancel{24}}{\cancel{24}}}{120 + \dfrac{12 \cdot 7 \cdot \cancel{5} \cdot \cancel{24}}{\cancel{5} \cdot \cancel{24}}} & \text{Factor and cancel} \\[25pt] & = & \dfrac{(12 \cdot 24) - (7 \cdot 5)}{120 + (12 \cdot 7)} & \\[10pt] & = & \dfrac{288 - 35}{120 + 84} & \\[10pt] & = & \dfrac{253}{204} & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f37836256c0a5f8570f363d267813960_l3.png)
![]() and
and ![]() have no common factors, thus our result is in lowest terms and we are done.
have no common factors, thus our result is in lowest terms and we are done.
Example 0.1.1.5
Perform the indicated operations and simplify. By `simplify’ here, we mean to have the final answer written in the form ![]() where
where ![]() and
and ![]() are integers which have no common factors. Said another way, we want
are integers which have no common factors. Said another way, we want ![]() in `lowest terms’.
in `lowest terms’.
![]()
Solution:
Simplify ![]() .
.
This fraction may look simpler than the one before it, but the negative signs and parentheses mean that we shouldn’t get complacent. Again we note that the division line here acts as a grouping symbol. That is,
![]()
This means that we should simplify the numerator and denominator first, then perform the division last. We begin in the parentheses, giving multiplication priority over addition and subtraction.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{(2(2)+1)(-3-(-3)) - 5(4-7)}{4-2(3)} & = & \dfrac{(4+1)(-3+3)-5(-3)}{4 - 6} & \\ [8pt] & = & \dfrac{(5)(0) + 15}{-2} & \\ [8pt] & = & \dfrac{15}{-2} & \\ [8pt] & = & -\dfrac{15}{2} & \text{Properties of Negatives} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9bddcea6dd01c21041c542e63d9ac4a6_l3.png)
As ![]() and
and ![]() have no common factors, we are done.
have no common factors, we are done.
Example 0.1.1.6
Perform the indicated operations and simplify. By `simplify’ here, we mean to have the final answer written in the form ![]() where
where ![]() and
and ![]() are integers which have no common factors. Said another way, we want
are integers which have no common factors. Said another way, we want ![]() in `lowest terms’.
in `lowest terms’.
![]()
Solution:
Simplify ![]() .
.
In this problem, we have multiplication and subtraction. Multiplication takes precedence so we perform it first. Recall that to multiply fractions, we do not need to obtain common denominators; rather, we multiply the corresponding numerators together along with the corresponding denominators. Like the previous example, we have parentheses and negative signs for added fun!
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \left(\dfrac{3}{5} \right) \left(\dfrac{5}{13} \right) - \left(\dfrac{4}{5}\right) \left( - \dfrac{12}{13}\right) & = & \dfrac{3 \cdot 5}{5 \cdot 13} - \dfrac{4\cdot (-12)}{5 \cdot 13} & \text{Multiply fractions}\\ [8pt] & = & \dfrac{15}{65} - \dfrac{-48}{65} & \\[10pt] & = & \dfrac{15}{65} + \dfrac{48}{65} & \text{Properties of Negatives}\\[10pt] & = & \dfrac{15+48}{65} & \text{Add numerators} \\ [10pt] & = & \dfrac{63}{65} & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-29e5aeadf45d9ce05ce45e50347252fd_l3.png)
![]() and
and ![]() have no common factors, so our answer
have no common factors, so our answer ![]() is in lowest terms and we are done.
is in lowest terms and we are done.
Of the issues discussed in the previous set of examples none cause students more trouble than simplifying compound fractions. We presented two different methods for simplifying them: one in which we simplified the overall numerator and denominator and then performed the division and one in which we removed the compound nature of the fraction at the very beginning. We encourage the reader to go back and use both methods on each of the compound fractions presented. Keep in mind that when a compound fraction is encountered in the rest of the text it will usually be simplified using only one method and we may not choose your favorite method. Feel free to use the other one in your notes.
Next, we review exponents and their properties. Recall that ![]() can be written as
can be written as ![]() because exponential notation expresses repeated multiplication. In the expression
because exponential notation expresses repeated multiplication. In the expression ![]() ,
, ![]() is called the base and
is called the base and ![]() is called the exponent. In order to generalize exponents from natural numbers to the integers, and eventually to rational and real numbers, it is helpful to think of the exponent as a count of the number of factors of the base we are multiplying by
is called the exponent. In order to generalize exponents from natural numbers to the integers, and eventually to rational and real numbers, it is helpful to think of the exponent as a count of the number of factors of the base we are multiplying by ![]() . For instance,
. For instance,
![]()
From this, it makes sense that
![]()
What about ![]() ? The `
? The `![]() ‘ in the exponent indicates that we are `taking away’ three factors of two, essentially dividing by three factors of two. So,
‘ in the exponent indicates that we are `taking away’ three factors of two, essentially dividing by three factors of two. So,
![]()
We summarize the properties of integer exponents below.
Properties of Integer Exponents
Suppose ![]() and
and ![]() are nonzero real numbers and
are nonzero real numbers and ![]() and
and ![]() are integers.
are integers.
- Product Rules:
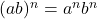 and
and 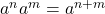 .
. - Quotient Rules:
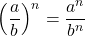 and
and 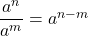 .
. - Power Rule:
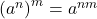 .
. - Negatives in Exponents:
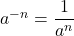 .
.
In particular,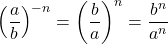 and
and 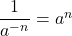 .
. - Zero Powers:
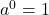 .
.
Note: The expression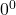 is an indeterminate form.[13]
is an indeterminate form.[13] - Powers of Zero: For any natural number
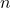 ,
, 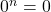 .
.
Note: The expression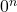 for integers
for integers 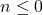 is not defined.
is not defined.
While it is important to state the Properties of Exponents, it is also equally important to take a moment to discuss one of the most common errors in Algebra. It is true that ![]() (which some students refer to as `distributing’ the exponent to each factor) but you cannot do this sort of thing with addition. That is, in general,
(which some students refer to as `distributing’ the exponent to each factor) but you cannot do this sort of thing with addition. That is, in general, ![]() . (For example, explore
. (For example, explore ![]() and
and ![]() .) The same goes for any other powers.
.) The same goes for any other powers.
With exponents now in the mix, we can now state the Order of Operations Agreement.
Order of Operations Agreement
When evaluating an expression involving real numbers:
- Evaluate any expressions in parentheses (or other grouping symbols).
- Evaluate exponents.
- Evaluate multiplication and division as you read from left to right.
- Evaluate addition and subtraction as you read from left to right.
We note that there are many useful mnemonic devices for remembering the order of operations.[14]
An example of the Order of Operations Agreement is ![]() . Students get into trouble is with expressions like
. Students get into trouble is with expressions like ![]() . If we think of this as
. If we think of this as ![]() , then it is clear that we evaluate the exponent first:
, then it is clear that we evaluate the exponent first: ![]() . In general, we interpret
. In general, we interpret ![]() . If we want the `negative’ to also be raised to a power, we must write
. If we want the `negative’ to also be raised to a power, we must write ![]() instead. To summarize,
instead. To summarize, ![]() and
and ![]() .
.
Of course, many of the `properties’ we’ve stated in this section can be viewed as ways to circumvent the order of operations. We’ve already seen how the distributive property allows us to simplify ![]() by performing the indicated multiplication before the addition that’s in parentheses. Similarly, consider trying to evaluate
by performing the indicated multiplication before the addition that’s in parentheses. Similarly, consider trying to evaluate ![]() . The Order of Operations Agreement demands that the exponents be dealt with first, however, trying to compute
. The Order of Operations Agreement demands that the exponents be dealt with first, however, trying to compute ![]() is a challenge, even for a calculator. One of the Product Rules of Exponents, however, allow us to rewrite this product, essentially performing the multiplication first, to get:
is a challenge, even for a calculator. One of the Product Rules of Exponents, however, allow us to rewrite this product, essentially performing the multiplication first, to get: ![]() .
.
Let’s take a break and enjoy another example.
Example 0.1.2
Example 0.1.2.1
Perform the indicated operations and simplify.
![]()
Solution:
Simplify ![]() .
.
We begin working inside the parentheses, then deal with the exponents, before working through the other operations. As we saw in Example 0.1.1, the division here acts as a grouping symbol, so we save the division to the end.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclcl} \dfrac{(4-2)(2 \cdot 4)-(4)^2}{(4-2)^2} & = & \dfrac{(2)(8)-(4)^2}{(2)^2} \\[10 pt] & = & \dfrac{(2)(8)-16}{4} \\[10pt] & = & \dfrac{16-16}{4} \\[10pt] & = & \dfrac{0}{4} \\[10pt] & = & 0 \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-b0976be61bcb2715f3d2fa17f73faddb_l3.png)
Example 0.1.2.2
Perform the indicated operations and simplify.
![]()
Solution:
Simplify ![]() .
.
As before, we simplify what’s in the parentheses first, then work our way through the exponents, multiplication, and finally, the addition.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 12(-5)(-5+3)^{-4}+6(-5)^2(-4)(-5+3)^{-5} & = & 12(-5)(-2)^{-4} + 6(-5)^{2}(-4)(-2)^{-5} \\ [10pt] & = & 12(-5)\left(\dfrac{1}{(-2)^4}\right) + 6(-5)^{2}(-4)\left(\dfrac{1}{(-2)^5}\right)& \\[10pt] & = & 12(-5)\left(\dfrac{1}{16}\right) + 6(25)(-4)\left(\dfrac{1}{-32}\right)& \\[10pt] & = & (-60)\left(\dfrac{1}{16}\right) + (-600)\left(\dfrac{1}{-32}\right)& \\ [10pt] & = & \dfrac{-60}{16} + \left(\dfrac{-600}{-32}\right)& \\ [10pt] & = & \dfrac{-15\cdot \cancel{4}}{4 \cdot \cancel{4}} + \dfrac{-75 \cdot \cancel{8}}{-4 \cdot \cancel{8}} & \\ [10pt] & = & \dfrac{-15}{4} + \dfrac{-75}{-4} & \\ [10pt] & = & \dfrac{-15}{4} + \dfrac{75}{4} & \\ [10pt] & = & \dfrac{-15 + 75}{4} & \\ [10pt] & = & \dfrac{60}{4} & \\ [10pt] & = & 15 & \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-11ebcd128246214a37b752a56658ba0f_l3.png)
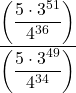
Example 0.1.2.3
Perform the indicated operations and simplify.
Solution:
Simplify  .
.
The Order of Operations Agreement mandates that we work within each set of parentheses first, giving precedence to the exponents, then the multiplication, and, finally the division. The trouble with this approach is that the exponents are so large that computation becomes a trifle unwieldy. What we observe, however, is that the bases of the exponential expressions, ![]() and
and ![]() , occur in both the numerator and denominator of the compound fraction. This gives us hope that we can use some of the Properties of Exponents (the Quotient Rule, in particular) to help us out. Our first step here is to invert and multiply. We see immediately that the
, occur in both the numerator and denominator of the compound fraction. This gives us hope that we can use some of the Properties of Exponents (the Quotient Rule, in particular) to help us out. Our first step here is to invert and multiply. We see immediately that the ![]() ‘s divide out after which we group the powers of
‘s divide out after which we group the powers of ![]() together and the powers of
together and the powers of ![]() together and apply the properties of exponents.
together and apply the properties of exponents.
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \dfrac{\left(\dfrac{5\cdot 3^{51}}{4^{36}}\right)}{\left(\dfrac{5 \cdot 3^{49}}{4^{34}}\right)} & = & \dfrac{5\cdot 3^{51}}{4^{36}} \cdot \dfrac{4^{34}}{5 \cdot 3^{49}} \\[10pt] & = & \dfrac{\cancel{5} \cdot 3^{51} \cdot 4^{34}}{\cancel{5} \cdot 3^{49} \cdot 4^{36}} \\[10pt] & = & \dfrac{3^{51}}{3^{49}} \cdot\dfrac{4^{34}}{4^{36}} \\[10pt] & = & 3^{51-49} \cdot 4^{34-36} \\ & = & 3^{2} \cdot 4^{-2} \\ & = & 3^{2} \cdot \left( \dfrac{1}{4^2}\right) \\[10pt] & = & 9 \cdot \left(\dfrac{1}{16} \right) \\[10pt] & = & \dfrac{9}{16} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-f4ba9ec7327fe72d5fe5707f048c44cd_l3.png)
Example 0.1.2.4
Perform the indicated operations and simplify.
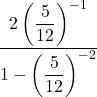
Solution:
Simplify 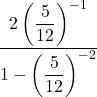 .
.
We have yet another instance of a compound fraction so our first order of business is to rid ourselves of the compound nature of the fraction like we did in Example 0.1.1. To do this, however, we need to tend to the exponents first so that we can determine what common denominator is needed to simplify the fraction.
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \dfrac{2 \left(\dfrac{5}{12}\right)^{-1}}{1 - \left(\dfrac{5}{12}\right)^{-2}} & = & \dfrac{2 \left(\dfrac{12}{5}\right)}{1 - \left(\dfrac{12}{5}\right)^{2}} \\[30pt] & = & \dfrac{\left(\dfrac{24}{5}\right)}{1 - \left(\dfrac{12^2}{5^2}\right)} \\[30pt] & = & \dfrac{\left(\dfrac{24}{5}\right)}{1 - \left(\dfrac{144}{25}\right)} \\ [30pt] & = & \dfrac{\left(\dfrac{24}{5}\right) \cdot 25}{\left(1 - \dfrac{144}{25}\right)\cdot 25} \\[30pt] & = & \dfrac{\left(\dfrac{24\cdot 5 \cdot \cancel{5}}{\cancel{5}}\right)}{\left(1 \cdot 25 - \dfrac{144 \cdot \cancel{25}}{\cancel{25}}\right)} \\[30pt] & = & \dfrac{120}{25-144} \\ [10pt] & = & \dfrac{120}{-119} \\[10pt] & = & -\dfrac{120}{119} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-cb319dc3192ce803be79aa0e310d81e2_l3.png)
Because ![]() and
and ![]() have no common factors, we are done.
have no common factors, we are done.
We close our review of real number arithmetic with a discussion of roots and radical notation. Just as subtraction and division were defined in terms of the inverse of addition and multiplication, respectively, we define roots by undoing natural number exponents.
Definition 0.2
Let ![]() be a real number and let
be a real number and let ![]() be a natural number. If
be a natural number. If ![]() is odd, then the principal
is odd, then the principal ![]() root of
root of ![]() (denoted
(denoted ![]() ) is the unique real number satisfying
) is the unique real number satisfying ![]() .
.
If ![]() is even,
is even, ![]() is defined similarly provided
is defined similarly provided ![]() and
and ![]() .
.
The number ![]() is called the index of the root and the number
is called the index of the root and the number ![]() is called the radicand.
is called the radicand.
For ![]() , we write
, we write ![]() instead of
instead of ![]() .
.
The reasons for the added stipulations for even-indexed roots in Definition 0.2 can be found in the Properties of Negatives. First, for all real numbers, ![]() , which means it is never negative. Thus if
, which means it is never negative. Thus if ![]() is a negative real number, there are no real numbers
is a negative real number, there are no real numbers ![]() with
with ![]() . This is why if
. This is why if ![]() is even,
is even, ![]() only exists if
only exists if ![]() . The second restriction for even-indexed roots is that
. The second restriction for even-indexed roots is that ![]() . This comes from the fact that
. This comes from the fact that ![]() , and we require
, and we require ![]() to have just one value. So even though
to have just one value. So even though ![]() and
and ![]() , we require
, we require ![]() and ignore
and ignore ![]() .
.
Dealing with odd powers is much easier. For example, ![]() has one and only one real solution, namely
has one and only one real solution, namely ![]() , which means not only does
, which means not only does ![]() exist, there is only one choice, namely
exist, there is only one choice, namely ![]() . Of course, when it comes to solving
. Of course, when it comes to solving ![]() , it’s not so clear that there is one and only one real solution, let alone that the solution is
, it’s not so clear that there is one and only one real solution, let alone that the solution is ![]() . Such pills are easier to swallow once we’ve thought a bit about such equations graphically,[15] and ultimately, these things come from the completeness property of the real numbers mentioned earlier.
. Such pills are easier to swallow once we’ve thought a bit about such equations graphically,[15] and ultimately, these things come from the completeness property of the real numbers mentioned earlier.
We list properties of radicals below as a `theorem’ as opposed to a definition because they can be justified using the properties of exponents.
Theorem 0.1 Properties of Radicals
Let ![]() and
and ![]() be real numbers and let
be real numbers and let ![]() and
and ![]() be natural numbers. If
be natural numbers. If ![]() and
and ![]() are real numbers, then
are real numbers, then
- Product Rule:
![Rendered by QuickLaTeX.com \sqrt[n]{ab} = \sqrt[n]{a} \, \sqrt[n]{b}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-1122c869f606673b61230b9ef4025794_l3.png)
- Quotient Rule:
![Rendered by QuickLaTeX.com \sqrt[n]{\dfrac{a}{b}} = \dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-35bf859f4f99724aad9a1f7d52424cc4_l3.png) , provided
, provided 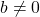 .
. - Power Rule:
![Rendered by QuickLaTeX.com \sqrt[n]{a^m} = \left(\sqrt[n]{a}\right)^m](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-54dd45c2f8abd7abb202c005122b727e_l3.png)
The proof of Theorem 0.1 is based on the definition of the principal ![]() root and the Properties of Exponents. To establish the product rule, consider the following. If
root and the Properties of Exponents. To establish the product rule, consider the following. If ![]() is odd, then by definition
is odd, then by definition ![]() is the unique real number such that
is the unique real number such that ![]() . Given that
. Given that ![]() as well, it must be the case that
as well, it must be the case that ![]() . If
. If ![]() is even, then
is even, then ![]() is the unique non-negative real number such that
is the unique non-negative real number such that ![]() . Note that because
. Note that because ![]() is even,
is even, ![]() and
and ![]() are also non-negative thus
are also non-negative thus ![]() as well. Proceeding as above, we find that
as well. Proceeding as above, we find that ![]() . The quotient rule is proved similarly and is left as an exercise. The power rule results from repeated application of the product rule, so long as
. The quotient rule is proved similarly and is left as an exercise. The power rule results from repeated application of the product rule, so long as ![]() is a real number to start with.[16] We leave that as an exercise as well.
is a real number to start with.[16] We leave that as an exercise as well.
We pause here to point out one of the most common errors students make when working with radicals. Obviously ![]() ,
, ![]() and
and ![]() . Thus we can clearly see that
. Thus we can clearly see that ![]() because we all know that
because we all know that ![]() . The authors urge you to never consider `distributing’ roots or exponents. It’s wrong and no good will come of it because in general
. The authors urge you to never consider `distributing’ roots or exponents. It’s wrong and no good will come of it because in general ![]() .
.
Due to the fact that radicals have properties inherited from exponents, they are often written as such. We define rational exponents in terms of radicals in the box below.
Definition 0.3
Let ![]() be a real number, let
be a real number, let ![]() be an integer and let
be an integer and let ![]() be a natural number.
be a natural number.
![Rendered by QuickLaTeX.com a^{\frac{1}{n}} = \sqrt[n]{a}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-8ffe1ffce2a0eb12a37737cfe7e36fee_l3.png) whenever
whenever ![Rendered by QuickLaTeX.com \sqrt[n]{a}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-ddacb8431cc6fa0d24161de8e2d5137d_l3.png) is a real number.[17]
is a real number.[17]![Rendered by QuickLaTeX.com a^{\frac{m}{n}} = \left(\sqrt[n]{a}\right)^m = \sqrt[n]{a^m}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-c18acceed044c0b594d63bc7139da411_l3.png) whenever
whenever ![Rendered by QuickLaTeX.com \sqrt[n]{a}](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-ddacb8431cc6fa0d24161de8e2d5137d_l3.png) is a real number.
is a real number.
It would make life really nice if the rational exponents defined in Definition 0.3 had all of the same properties that integer exponents have as listed previously – but they don’t. Why not? Let’s look at an example to see what goes wrong. Consider the Product Rule which says that ![]() and let
and let ![]() ,
, ![]() and
and ![]() . Plugging the values into the Product Rule yields the equation
. Plugging the values into the Product Rule yields the equation ![]() . The left side of this equation is
. The left side of this equation is ![]() which equals
which equals ![]() but the right side is undefined because neither root is a real number. Would it help if, when it comes to even roots (as signified by even denominators in the fractional exponents), we ensure that everything they apply to is non-negative? That works for some of the rules – we leave it as an exercise to see which ones – but does not work for the Power Rule.
but the right side is undefined because neither root is a real number. Would it help if, when it comes to even roots (as signified by even denominators in the fractional exponents), we ensure that everything they apply to is non-negative? That works for some of the rules – we leave it as an exercise to see which ones – but does not work for the Power Rule.
Consider the expression ![]() . Applying the usual laws of exponents, we’d be tempted to simplify this as
. Applying the usual laws of exponents, we’d be tempted to simplify this as ![]() . However, if we substitute
. However, if we substitute ![]() and apply Definition 0.3, we find
and apply Definition 0.3, we find ![]() so that
so that ![]() . Thus in this case we have
. Thus in this case we have ![]() even though all of the roots were defined. It is true, however, that
even though all of the roots were defined. It is true, however, that ![]() and we leave this for the reader to show. The moral of the story is that when simplifying powers of rational exponents where the base is negative or worse, unknown, it’s usually best to rewrite them as radicals.
and we leave this for the reader to show. The moral of the story is that when simplifying powers of rational exponents where the base is negative or worse, unknown, it’s usually best to rewrite them as radicals.
Example 0.1.3
Example 0.1.3.1
Perform the indicated operations and simplify.
![]()
Solution:
Simplify ![]() .
.
We begin in the numerator and note that the radical here acts a grouping symbol,[18] so our first order of business is to simplify the radicand.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{-(-4) -\sqrt{(-4)^2-4(2)(-3)}}{2(2)} & = & \dfrac{-(-4) - \sqrt{16-4(2)(-3)}}{2(2)} & \\[10pt] & = & \dfrac{-(-4) - \sqrt{16-4(-6)}}{2(2)} & \\[10pt] & = & \dfrac{-(-4) - \sqrt{16-(-24)}}{2(2)} & \\[10pt] & = & \dfrac{-(-4) - \sqrt{16+24}}{2(2)} & \\[10pt] & = & \dfrac{-(-4) - \sqrt{40}}{2(2)} & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-efb30314bed540997d443e942e330fc9_l3.png)
As you may recall, ![]() can be factored using a perfect square as
can be factored using a perfect square as ![]() so we use the product rule of radicals to write
so we use the product rule of radicals to write ![]() . This lets us factor a `
. This lets us factor a `![]() ‘ out of both terms in the numerator, eventually allowing us to divide by a factor of
‘ out of both terms in the numerator, eventually allowing us to divide by a factor of ![]() in the denominator.
in the denominator.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{-(-4) - \sqrt{40}}{2(2)} & = & \dfrac{-(-4) - 2\sqrt{10}}{2(2)} & \\[10pt] & = & \dfrac{4 - 2\sqrt{10}}{2(2)} & \\ [10pt] & = & \dfrac{2 \cdot 2 - 2\sqrt{10}}{2(2)} & \\[10pt] & = & \dfrac{2(2 - \sqrt{10})}{2(2)} \\ [12pt] & = & \dfrac{\cancel{2}(2 - \sqrt{10})}{\cancel{2}(2)} & \\[12pt] & = & \dfrac{2 - \sqrt{10}}{2} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-0a5a097a08d36db4e7e494967b18d816_l3.png)
Now that the numerator and denominator have no more common factors,[19] we are done.
Example 0.1.3.2
Perform the indicated operations and simplify.
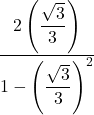
Solution:
Simplify 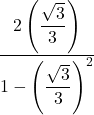 .
.
Once again we have a compound fraction, so we first simplify the exponent in the denominator to see which factor we’ll need to multiply by in order to clean up the fraction.
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{2 \left( \dfrac{\sqrt{3}}{3}\right)}{1 - \left( \dfrac{\sqrt{3}}{3} \right)^2} & = & \dfrac{2 \left( \dfrac{\sqrt{3}}{3}\right)}{1 - \left( \dfrac{(\sqrt{3})^2}{3^2} \right)} & \\[25pt] & = & \dfrac{2 \left( \dfrac{\sqrt{3}}{3}\right)}{1 - \left( \dfrac{3}{9} \right)} &\\[25pt] & = & \dfrac{2 \left( \dfrac{\sqrt{3}}{3}\right)}{1 - \left( \dfrac{1 \cdot \cancel{3}}{3 \cdot \cancel{3}} \right)} & \\[25pt] & = & \dfrac{2 \left( \dfrac{\sqrt{3}}{3}\right)}{1 - \left( \dfrac{1}{3} \right)} & \\[25pt] & = & \dfrac{2 \left( \dfrac{\sqrt{3}}{3}\right) \cdot 3}{\left(1 - \left( \dfrac{1}{3} \right)\right) \cdot 3} & \\[25pt] & = & \dfrac{\dfrac{2 \cdot \sqrt{3} \cdot \cancel{3}}{\cancel{3}}}{1\cdot 3 - \dfrac{1\cdot \cancel{3}}{\cancel{3}}}& \\[25pt] & = & \dfrac{2 \sqrt{3}}{3 - 1} & \\[10pt] & = & \dfrac{\cancel{2} \sqrt{3}}{\cancel{2}} & \\[10pt] & = & \sqrt{3} & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-ed8146f3ab4c2a1ab924b1269a5d09c3_l3.png)
Example 0.1.3.3
Perform the indicated operations and simplify.
![]()
Solution:
Simplify ![]() .
.
Working inside the parentheses, we first encounter ![]() . While the
. While the ![]() isn’t a perfect cube,[20] we may think of
isn’t a perfect cube,[20] we may think of ![]() .
.
Because ![]() , which is a perfect cube, we may write
, which is a perfect cube, we may write
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} \sqrt[3]{-2} & = &\sqrt[3]{(-1)(2)} \\ &=& \sqrt[3]{-1} \sqrt[3]{2} \\ &=& - \sqrt[3]{2}\\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-777bebf58c8bd709dc4e971aeef7c96b_l3.png)
When it comes to ![]() , we may write it as
, we may write it as
![]()
So,
![]()
At this stage, we can simplify ![]() . You may remember this as being called `combining like radicals,’ but it is in fact just another application of the distributive property:
. You may remember this as being called `combining like radicals,’ but it is in fact just another application of the distributive property:
![Rendered by QuickLaTeX.com \[\begin{array}{rcl} -\sqrt[3]{2} + 3\sqrt[3]{2} &=& (-1)\sqrt[3]{2} + 3 \sqrt[3]{2} \\ &=& (-1+3)\sqrt[3]{2} \\ &=& 2\sqrt[3]{2} \\ \end{array}\]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-18ec9cf4ae9481e2d2b3b1fa4ec74eda_l3.png)
Putting all this together, we get:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl} (\sqrt[3]{-2} - \sqrt[3]{-54})^2 & = & (-\sqrt[3]{2} + 3 \sqrt[3]{2})^2 \\ & = & (2 \sqrt[3]{2})^2 \\ [5pt] & = & 2^2 (\sqrt[3]{2})^2 = 4 \sqrt[3]{2^2} \\[5pt] & = & 4 \sqrt[3]{4} \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-a55e16cf34e9682608c27180e954c07d_l3.png)
There are no perfect integer cubes which are factors of ![]() (apart from
(apart from ![]() , of course), so we are done.
, of course), so we are done.
Example 0.1.3.4
Perform the indicated operations and simplify.
![]()
Solution:
Simplify ![]() .
.
We start working in the parentheses and get a common denominator to subtract the fractions:
![Rendered by QuickLaTeX.com \[ \begin{array}{rcl}\dfrac{9}{4} - 3 &=& \dfrac{9}{4} - \dfrac{3 \cdot 4}{1 \cdot 4} \\[10pt] &=& \dfrac{9}{4} - \dfrac{12}{4} \\[10pt] &=& \dfrac{-3}{4} \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-98b92f555d0a81f96c84bdc884aee27c_l3.png)
The denominators in the fractional exponents are odd, so we can proceed by using the properties of exponents:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} 2 \left(\dfrac{9}{4} - 3\right)^{1/3} + 2\left(\dfrac{9}{4}\right)\left(\dfrac{1}{3}\right)\left(\dfrac{9}{4}-3\right)^{-2/3} & = &2 \left(\dfrac{-3}{4} \right)^{1/3} + 2\left(\dfrac{9}{4}\right)\left(\dfrac{1}{3}\right)\left(\dfrac{-3}{4}\right)^{-2/3} & \\ [8pt] & = & 2 \left(\dfrac{(-3)^{1/3}}{(4)^{1/3}} \right) + 2\left(\dfrac{9}{4}\right)\left(\dfrac{1}{3}\right)\left(\dfrac{4}{-3}\right)^{2/3} & \\ [8pt] & = & 2 \left(\dfrac{(-3)^{1/3}}{(4)^{1/3}} \right) + 2\left(\dfrac{9}{4}\right)\left(\dfrac{1}{3}\right)\left(\dfrac{(4)^{2/3}}{(-3)^{2/3}}\right) & \\ [8pt] & = & \dfrac{2 \cdot (-3)^{1/3}}{4^{1/3}} + \dfrac{2 \cdot 9 \cdot 1 \cdot 4^{2/3}}{4 \cdot 3 \cdot (-3)^{2/3}} & \\ [8pt] & = & \dfrac{2 \cdot (-3)^{1/3}}{4^{1/3}} + \dfrac{\cancel{2} \cdot 3 \cdot \cancel{3} \cdot 4^{2/3}}{2 \cdot \cancel{2} \cdot \cancel{3} \cdot (-3)^{2/3}} & \\ [8pt] & = & \dfrac{2 \cdot (-3)^{1/3}}{4^{1/3}} + \dfrac{3 \cdot 4^{2/3}}{2 \cdot (-3)^{2/3}} & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-fe103fb1e66481222cbaa5f8941b48e4_l3.png)
At this point, we could start looking for common denominators but it turns out that these fractions reduce even further. Due to the fact that ![]() , then
, then ![]() . Similarly,
. Similarly, ![]() .
.
The expressions ![]() and
and ![]() contain negative bases so we proceed with caution and convert them back to radical notation to get:
contain negative bases so we proceed with caution and convert them back to radical notation to get:
![]()
Hence:
![Rendered by QuickLaTeX.com \[ \begin{array}{rclr} \dfrac{2 \cdot (-3)^{1/3}}{4^{1/3}} + \dfrac{3 \cdot 4^{2/3}}{2 \cdot (-3)^{2/3}} & = & \dfrac{2 \cdot (-3^{1/3})}{2^{2/3}} + \dfrac{3 \cdot 2^{4/3}}{2 \cdot 3^{2/3}} & \\ [5pt] & = & \dfrac{2^{1} \cdot (-3^{1/3})}{2^{2/3}} + \dfrac{3^{1} \cdot 2^{4/3}}{2^{1} \cdot 3^{2/3}} & \\ [5pt] & = & 2^{1 - 2/3} \cdot (-3^{1/3}) +3^{1- 2/3} \cdot 2^{4/3 - 1} & \\ [5pt] & = & 2^{1/3} \cdot (-3^{1/3}) +3^{1/3} \cdot 2^{1/3} & \\ [5pt] & = & - 2^{1/3} \cdot 3^{1/3} +3^{1/3} \cdot 2^{1/3} & \\ [5pt] & = & 0 & \\ \end{array} \]](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-9a9f1b856cd73fc601fa130ae31d6cc9_l3.png)
We close this section with a note about simplifying. In the preceding examples we used “nice” numbers because we wanted to show as many properties as we could per example. This then begs the question “What happens when the numbers are not nice?” Unfortunately, the answer is “Not much simplifying can be done.” Take, for example,
![]()
Sadly, that’s as good as it gets.
0.1.2 Section Exercises
In Exercises 1 – 33, perform the indicated operations and simplify.
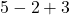
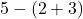
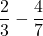
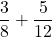
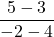
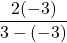
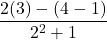
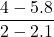
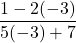
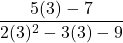
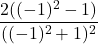
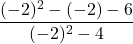
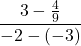
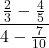
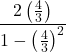
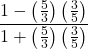
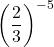
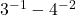
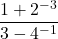
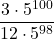
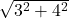

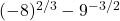
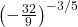
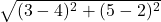
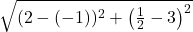
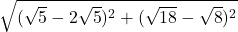
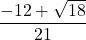
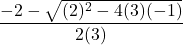
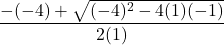
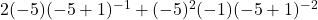
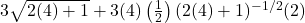
![Rendered by QuickLaTeX.com 2(-7)\sqrt[3]{1-(-7)} + (-7)^2 \left(\frac{1}{3}\right)(1-(-7))^{-2/3}(-1)](https://pressbooks.library.tamu.edu/app/uploads/quicklatex/quicklatex.com-edac7b37bc28623e5a95f02731831686_l3.png)
- Prove the Quotient Rule and Power Rule stated in Theorem 0.1.
- Discuss with your classmates how you might attempt to simplify the following:
Section 0.1 Exercise Answers can be found in the Appendix … Coming soon
- Math pun intended! ↵
- See, for instance, Landau's Foundations of Analysis. ↵
- The symbol
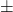 is read `plus or minus' and it is a shorthand notation which appears throughout the text. Just remember that
is read `plus or minus' and it is a shorthand notation which appears throughout the text. Just remember that 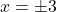 means
means 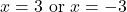 . ↵
. ↵ - The expression
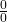 is technically an `indeterminant form' as opposed to being strictly `undefined' meaning that with Calculus we can make some sense of it in certain situations. We'll talk more about this in Chapter 3. ↵
is technically an `indeterminant form' as opposed to being strictly `undefined' meaning that with Calculus we can make some sense of it in certain situations. We'll talk more about this in Chapter 3. ↵ - Don't worry. We'll review this in due course. And, yes, this is our old friend the Distributive Property! ↵
- We're not just being lazy here. We looked at many of the big publishers' Precalculus books and none of them use different dashes, either. ↵
- The old `invert and multiply' or `fraction gymnastics' play. ↵
- Or `Dividing Out' Common Factors - this is really just reading the previous property `from right to left'. ↵
- See the remark on above about how we add
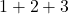 . ↵
. ↵ - We could have used
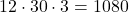 as our common denominator but then the numerators would become unnecessarily large. It's best to use the lowest common denominator. ↵
as our common denominator but then the numerators would become unnecessarily large. It's best to use the lowest common denominator. ↵ - Also called a `vinculum'. ↵
- Try it if you don't believe us. ↵
- See the comment regarding `
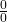 ' above. ↵
' above. ↵ - Our favorite is `Please entertain my dear auld Sasquatch.' ↵
- See Chapter 2. ↵
- Otherwise we'd run into an interesting paradox. See Section 0.5. ↵
- If
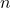 is even we need
is even we need 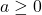 . ↵
. ↵ - The line extending horizontally from the square root symbol
 is, you guessed it, another vinculum. ↵
is, you guessed it, another vinculum. ↵ - Do you see why we aren't `dividing out' the remaining
 's? ↵
's? ↵ - Of an integer, that is! ↵
A real number is any number which possesses a decimal representation. The set of real numbers is denoted by the character [latex]\mathbb{R}[/latex].
The periods of ellipsis `[latex]\ldots[/latex]' here indicate that the natural numbers contain 1, 2, 3 `and so forth'.
The natural numbers plus 0.
The whole numbers plus the opposites of the natural numbers.
Rational numbers are the ratios of integers where the denominator is not zero.
An irrational number is a real number, which isn't rational.